Интеллектуальные игры, подобные головоломкам, дисциплинируют мышление, формируют мыслительную культуру, значение которой трудно переоценить, развивают воображение, причем, все эти собственные усовершенствования человек приобретает в самой захватывающей форме – в форме игры.

---

Совсем немного истории

Головоломка «Instant Insanity» (Мгновенное Безумие), возможно, одна из самых востребованных для иллюстрации применимости теории графов в решении задач подобного ей типа. Во всяком случае, на youtube вы найдете много примеров такого именно её использования немалым числом преподавателей математики. Трудно сказать, как давно известна сама эта головоломка, но она была достаточно популярна для того, чтобы ещё в 1947 году обратить на себя внимание одного из членов студенческого математического «Архимедова общества» Кембриджского университета, скрывавшегося за псевдонимом «F. De Carteblanche» (настоящее его имя, по информации известного коллекционера и хронолога головоломок Роберта Штегмана/Rob Stegmann – Cedric A. B. Smith), и быть отмеченной в публикации периодического издания «Eureka» №9 (1947) общества «The Archimedeans». После публикации изящного решения F. De Carteblanche, и до сегодняшнего дня, математики находят поводы, чтобы возвращаться время от времени к этой задаче, и к классу происходящих от нее задач.

Сама головоломка представляет собой 4 кубика, раскрашенные в 4 цвета, которые предлагается уложить в ряд таким образом, чтобы на каждой стороне получившейся призмы/пирамиды были представлены все 4 цвета. Для краткости и удобства, часто пользуются обозначением для самой пирамиды «1х1х4».

Коммерческое имя «Instant Insanity» закрепилось за этой головоломкой в конце 1960-х. Другие известные торговые её имена – это «Tantaliser», «Crazy Cubes», и найдется с дюжину других, известных менее, но достаточно распространенных, не мало также клонов, представляющих её модификации.

В 1969 году журнале «Наука и жизнь», номере 2, появилась небольшая заметка об этой головоломке от Бронислава Ивановича Колтового, известного популяризатора науки, большого любителя головоломок и автора многочисленных книг, посвященных головоломкам и занимательным математическим задачам. Позднее, по меньшей мере, две фабрики игрушек в СССР, в Одессе и Кирове (ПО «Вятка») выпускали эту головоломку.


Рис. 1. Головоломка, выпускавшаяся в 1970-х годах ПО «Вятка», г. Киров

Головоломка, действительно, очень увлекательна, так как все те особенности, что делают игру подобного рода популярной, в ней присутствуют: она умеренно сложна, и обладает привлекательным дизайном – она решается не более чем за 8 шагов, и может быть сколь угодно компактна.

Головоломка на фотографии, хранящаяся у меня более 40 лет, в англоязычной литературе зовется «головоломкой с одним решением» (иногда употребляется еще выражение «simple solution/простое решение»). Такое название может показаться не самым очевидным, и ниже я объясню его происхождение.

Я обязательно приведу здесь и графическое решение головоломки, но ранее этого я бы хотел ввести некоторые определения, назначенные упростить мне дальнейшее изложение материала.

Ради чего, собственно?

Много ли существует наборов кубиков по четыре, обладающих «одним решением»? – Мне нигде не встретились попытки осуществить такой подсчет, хотя он чрезвычайно прост, зато встретились указания на патенты, защищающие права владельцев, включавшие как торговое имя игры, так и саму комбинацию раскрашенных кубиков. Мысль же такой подсчет произвести пришла сразу вслед за мыслью написать компьютерную версию головоломки. Может показаться, что задача нахождения всех возможных комбинаций кубиков с «одним решением» слишком узкая, специфическая, однако использованный мною для поиска массива четырехэлементных сборок подход может оказаться весьма удобным для описания и формализации других задач с кубиками, и для решения этих задач.

Собственно цель данной статьи, кроме того, чтобы развлечь читателя примерами пространственно-цветовых превращений четырехэлементных сборок кубиков, состоит ещё и в том, чтобы предложить сообществу увлеченно обсуждающих головоломки, подобные той, о которой идет речь, простой, лаконичный и понятный язык описания состояний такого, как кубик объекта, вместо пространных и мучительных «развертка номер 2, повернуть вокруг оси Z, в правосторонней системе..» и т. д. Любой, кому приходится, хотя бы изредка, утомлять своё воображение за чтением подобных фраз, полагаю, досадовал на отсутствие более кратких и выразительных приемов описания состояния обсуждаемого объекта. Особенно возмущают пространные описания состояний объектов программистов, мыслительная культура которых изощрена привычкой к формализации, логике и алгоритмизации.

Попробуем формализовать несколько простых наблюдений над кубиками.

Некоторые соглашения об обозначениях и терминологии

Для целей удобства использования в дальнейшем, проиндексируем грани куба следующим образом (см. Рис. 2):
0 – нижняя грань, 1 – лицевая грань, 2 – верхняя грань, 3 – задняя, 4 – левая боковая, 5 – правая боковая.


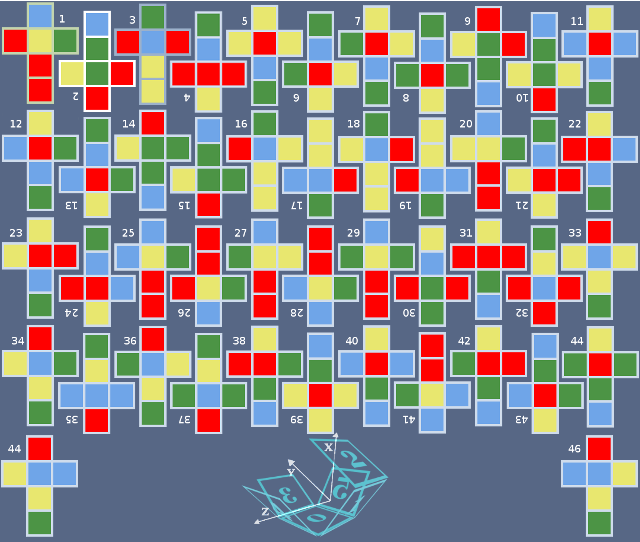
Рис. 2. Развертки кубиков

Опишем все возможные повороты кубика в его локальной правосторонней системе координат, в которой расположим кубик таким образом, чтобы центры кубиков, составленных в ряд, оказались на оси Z, а ось X при этом была направлена вверх.


Рис. 3. Индексированные повороты

Буквой обозначим поворот на 90 градусов вокруг соответствующей оси, знак «минус» перед ней указывает, что поворот осуществлен на -90 градусов.

В такой форме записи легко фиксировать пространственное положение куба, сколь угодно сложную последовательность поворотов он бы не выполнял: например, получить последовательность индексов для поворотов (X,X) можно переставив в соответствующем графе «индексы» таблицы порядке исходное положение индексов кубика.

Удобная форма записи – располагая преобразуемые индексы сверху вниз, от исходного положения к новому пространственному перемещению кубика.

Графическое решение

Отчего же оно «единственное», если кубики, в строгом соответствии с требованиями головоломки, очевидно могут образовывать несколько различных пространственных комбинаций?


Рис. 4. Собранная головоломка

Потому что «правильная» головоломка имеет единственное графическое решение!
Чтобы повторить решение F. De Carteblanche, нам потребуется краткий экскурс в теорию графов, причем знания, нам требующиеся, столь незначительны, что люди, не слышавшие до сих пор об этой области математики, едва ли новое знание ощутят как «багаж».

Каждый куб в представлении графов может быть записан как комбинация его противоположных сторон – для примера возьмем куб с номером 27 (Рис.2), его запись выглядит следующим образом: RY/RB/GY.

• Порядок записи граней и самих цветов в гранях не имеет значения, что прямо указывает на инвариантность перестановок граней у отдельного кубика к состоянию решения головоломки. Факт этот кажется не самым ожидаемым, оттого несколько удивительным: поменяв, например, две противоположные грани куба дважды, мы получим этот же куб, но в другом пространственном положении, однако меняя грани один раз или три раза, мы имеем куб совершенно другой, однако он в сочетании с тремя прежними кубами набора опять образует головоломку, имеющую «простое решение». «Оживим» это наблюдение приемом индексной записи: выберем из таблицы разверток кубиков кубики с номерами 27, 16, 10, 5. Поскольку грани 4 и 5 у куба являются боковыми (в соответствии с соглашением), то очевидно, что развертки этих кубиков приведены на Рис. 2 в положении сборки (решения), приняв цифровое обозначение «красный — 0, желтый — 1, синий — 2, зеленый — 3» запишем:
  
  [001231] - кубик 27
[112301] - кубик 16
[233011] - кубик 10
[320111] - кубик 5
Именно эта сборка вращается на Рис. 4.

  поменяем местами противоположные грани первого куба, кроме его боковых граней, скрытых от наблюдателя: [120031] – но это тот же куб, только в положении 230145 (Z,Z); поменяем местами грани с индексами 0 и 2: [100231] – куб в положении 210354 (Y,Y) займет прежнее место в сборке, за исключением того, что скрытые от наблюдателя боковые грани поменялись местами; поменяв местами грани с индексами 1 и 3 получим куб [021031], который после поворотов 032154 (X,X) так же станет [001213], как и предыдущий. Сборка в целом, между тем, как только мы вернем «модифицированный» кубик в прежнее положение, продолжит оставаться «решенной».
• Обратим внимание на повороты за номерами 4, 7, 8, 13, 16, 20, 22 из Таблицы индексированных поворотов (Рис. 3) – это те самые повороты, в которых участия не принимают боковые грани кубиков, и все эти повороты, примененные ко всем кубикам сборки одновременно, не ломают «решения» головоломки. Т.е. пространственно различных комбинаций кубиков, в которых может наблюдаться решение головоломки вообще-то… 8.
  

Однако, вернемся к графам. Нам достаточно представления о графе, как о неком множестве вершин (узлов, nodes), пребывающих в определенных между собой связях или, проще говоря, соединенных ребрами (связями, edges). Вершинами, в нашем случае, мы будем полагать цвета или сами цветные грани, а в качестве связей физическое ребро кубика уместно лишь в смысле указания на то, что выбранные на графе два цвета образуют пару в конкретной рассматриваемой реализации кубика. Если ребро замыкается на той же самой вершине, принято граф с такой конструкцией называть псевдографом, а соответствуюшее ребро петлёй (loop).

Решим графически головоломку на Рис. 5: в строчной записи, кубики, её составляющие, выглядят как YG/RB/RY, RY/GY/BY, GB/RG/YY, GR/YY/YB. Ниже каждого кубика поместим его представление в виде вершин и ребер соответствующего ему графа, после чего, объединим все четыре псевдографа в единую графическую конструкцию.

Собственно, именно над этим хитросплетением и предстоит нам поразмыслить, чтобы решить головоломку:

• внутри этого объединенного мультиграфа необходимо выделить два отдельных подграфа (два пути), каждый из которых только один раз проходит через все четыре цветовых вершины, используя при этом каждое из 4-х ребер, пронумерованных от 1 до 4-Х. Причем каждая вершина должна иметь лишь два исходящих ребра или только оба конца исходящей из нее петли. Один подграф будет представлять ряд кубиков в положении «решения головоломки», обращенных лицевой стороной к наблюдателю, второй – ряд кубиков в положении «сверху». Очевидно, что любое ребро не может быть использовано в обоих подграфах, т.к. одновременно представлять фронтальную и верхнюю части собранной призмы не может.

Рис. 5. Графическое решение головоломки

Оказывается, разделить мультиграф на два подграфа, соблюдая все эти условия, можно лишь одним образом. Отсюда, собственно, и произошло устойчивое выражение «единственное решение».
Если каждый из кубиков в его полученном размещении (индексированная запись на Рис. 5) повернуть в последовательности XXZ(103254), то мы узнаем в этой сборке уже нам знакомые кубики 27, 16, 10, 5.

Разумеется, существуют наборы кубиков по 4-е, не имеющие ни единого решения, как и те, что имеют решений слишком много, чтобы комбинирование их казалось занимательным.
Вообще, мне продолжает казаться, что я продолжаю эксплуатировать заимствованный речевой штамп – «единственное решение» образом не самым удачным, но быть может лаконичное и точное определение для сборок с минимально возможным числом требуемых по условию задачи комбинаций кто-то вскоре предложит. Лично же у меня, любая комбинация кубиков, допускающая большее число комбинаций для сборки, нежели минимально возможное, вызывает некоторое затруднение с её классифицированием.


Рис.6. Пример сборки с 24-мя решениями

Так и сколько же их?

Я не хотел, чтобы в мобильной версии моей головоломки некоторая комбинация кубиков примелькалась и наскучила игроку, и не надеялся, что 24 варианта возможного перекрашивания набора кубиков способны надолго ввести в заблуждение пытливые умы.
Кроме того, просто интересно самому: сколько всего существует уникальных комбинаций четырехцветных кубиков по 4-е, являющихся комбинациями с «одним решением», и не являющимися «перекрашиванием» самих себя?

Можно просто взять все 68 возможных раскрасок кубиков (именно такое число раскрасок в 4-е цвета указывает лемма Бёрнсайда) и простым перебором «по 4-е из 68-ми» все эти комбинации найти (попутно проверяя их на «единственность» и «перекрашивания») – способ этот, однако, не отличается изяществом и обещает быть весьма затратным по времени машинного расчета (более чем в 30 раз от принятого мною, как впоследствии показали сравнения). Оптимальным мне показалось строить сразу возможные комбинации кубиков по 4-е. Кроме того, внимательный взгляд на индексную форму записи пространственных положений кубика (Таблица, Рис.3), позволяет произвести некоторую оптимизацию такого «перебора»:

• запись через индексы позволяет легко определить, какие цветовые модели раскраски кубика не могут встречаться в сборках с «единственным» (минимальным набором удовлетворяющих условиям головоломки комбинаций) решением: 12 кубиков, использованных Rob Stegmann в его наборе из 56, как раз не подходят для таких сборок, оттого группы 5 и 6, в его классификации, нигде в «простых» решениях не появились.
• Отсеяв «негодные» цветовые модели еще до стадии моделирования самих сборок по 4 кубика, можно существенно сократить время перебора комбинаций кубиков для сборок.
• Эти фильтры уместно использовать, как в головоломках с трехцветной раскраской кубиков (есть и такие, но здесь мы их не рассматриваем), так и в случае четырехцветной раскраски.

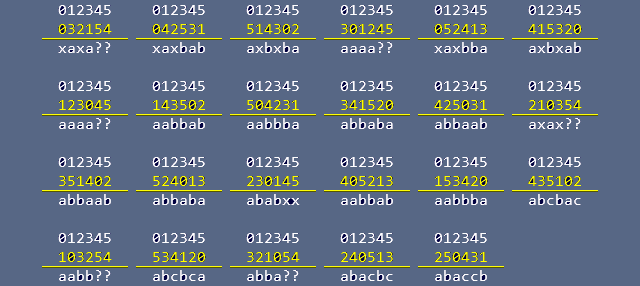
Рис.7. Недопустимые последовательности

Легко видеть из Рис.7, что кубики, имеющие одинаково закрашенные противоположные или смежные не боковые грани, а также кубики, закраска боковых граней которых повторяет закраску каких-либо из не боковых граней, не могут присутствовать в сборках с «одним решением», т.к. порождают новые, дополнительные решения.

Надо заметить, что и вполне «годные» кубики легко создают сборки не удовлетворяющие критерию «единственности решения»: например, комбинация на Рис.6, в которой синхронное помещение кубиков сборки в любой из 24-х возможных его пространственных положений оставляет сборку «решенной», образована как раз «годными» кубиками с номерами 25, 17, 15, 23.

«Не перекрашенных» сборок с «одним решением» набралось 1073 за время чуть превышающее минуту работы моего компьютера, и именно эти 46 кубиков, из которых все эти сборки комбинируются, представлены на Рис. 2. Меня несколько обескуражило, что в этом наборе отсутствуют еще 10 кубиков, раскраски которых я предполагал увидеть, т.к. они вполне отвечали сформулированным мною требованиям. Тогда я добавил их первыми в массив «моих» кубиков и прогнал уже обычный "злобный brute force" – в результате сгенерированный массив сборок так и продолжал оставаться числом в 1073, изменился лишь набор использовавшихся для этих сборок кубиков: четыре кубика из «новых» добавились к моему набору, но вытеснили два ранее бывших в наборе кубика… Тот же результат получился и для массива в 68 кубиков, сгенерированного исключительно из принципа уникальности раскраски.
Магическое число 1073.

Перекрашивание

Действительно ли, перекрашивая 1073 сборки 24-мя способами я получу 24х1073 вариантов головоломок? – Совсем нет.

Взглянем на сборку (все развертки из Рис. 2)

[001233] - кубик 29
[123300] - кубик 30
[230121] - кубик 17 в положении XX-Y (534120)
[312000] - кубик 32

Сборка приведена в положении решения. Перекрасим её грани следующим образом: желтый – в синий, синий – в желтый, иначе 1 – 2, 2 – 1:

[002133] - и повернем на XXZ (103254)] : [001233] - кубик 29
[213300] - и повернем на XXZ (103254)] : [123300] - кубик 30
[130212] - и повернем на XXZ (103254)] : [312021] - кубик 46
[321000] - и повернем на XXZ (103254)] : [230100] - кубик 31

Т.е., в данном примере, создать новую сущность перекрашиванием не удалось (любые сборки, образуемые из приведенного на Рис. 2 набора, уже учтены среди существующих 1073-х ) – одна из сборок существующих в наборе, перекрашена в другую (из других кубиков) также уже учтенную нами. Тем не менее, «перекрашивание» создаст немалое количество «неузнаваемо» выглядящих головоломок.

«Что же из этого следует?»

Будет чрезвычайно досадно, если культура интеллектуального досуга уступит место культуре досуга созерцательного. Надеюсь, что их мирное сосуществование возможно.