Содержание

• Часть 1: Получаем данные

В прошлой части, удалось распарсить сайт Додо-пиццы и загрузить данные об ингредиентах, а самое главное — фотографии пицц. Всего в нашем распоряжении оказалось 20 пицц. Разумеется, формировать обучающие данные всего из 20 картинок не получится. Однако, можно воспользоваться осевой симметрией пиццы: выполнив вращение картинки с шагом в один градус и вертикальным отражением — позволяет превратить одну фотографию в набор из 720 изображений. Тоже мало, но всё же попытаемся.

Попробуем обучить Условный вариационный автоэнкордер (Conditional Variational Autoencoder), а потом перейдёт к тому, ради чего это всё и затевалось — генеративным cостязательным нейронным сетям (Generative Adversarial Networks).

CVAE — условный вариационный автоэнкордер

Для разбирательства с автоэнкодерами, поможет отличная серия статей:

• Автоэнкодеры в Keras, Часть 3: Вариационные автоэнкодеры (VAE)
• Автоэнкодеры в Keras, Часть 4: Conditional VAE

Настоятельно рекомендую к прочтению.
Здесь же перейдём сразу к делу.

Отличие CVAE от VAE — состоит в том, что нам нужно на вход как энкодеру, так и декодеру, дополнительно подавать еще метку. В нашем случае — меткой будет вектор рецепта, который получаем от OneHotEncoder.

Однако, тут возникает нюанс — а в какой момент имеет смысл подавать нашу метку?

Я попробовал два метода:

1. в конце — после всех свёрток — перед полносвязным слоем
2. в начале — после первой свёртки — добавляется как дополнительный канал

В принципе, оба способа имеют право на существование. Кажется логичным, что если добавлять метку в конце, то она будет привязываться к более высокоуровневым фичам изображения. И наоборот — если добавлять её в начале, то она будет привязана к более низкоуровневым фичам. Попробуем сравнить оба способа.

Вспомним, что рецепт состоит максимум из 9 ингредиентов. А их всего — 28. Получается, код рецепта будет представлять собой матрицу 9х29, а если вытянуть её, то получится 261-мерный вектор.

Для изображения, размером 32х32, выберем размер скрытого пространства равным 512.
Можно выбрать и меньше, но как будет видно далее — это приводит к более смазанному результату.

Код для энкодера с первым методом добавления метки — после всех свёрток:

def create_conv_cvae(channels, height, width, code_h, code_w):
    input_img = Input(shape=(channels, height, width))

    input_code = Input(shape=(code_h, code_w))
    flatten_code = Flatten()(input_code)

    latent_dim = 512
    m_height, m_width = int(height/4), int(width/4)

    x = Conv2D(32, (3, 3), activation='relu', padding='same')(input_img)
    x = MaxPooling2D(pool_size=(2, 2), padding='same')(x)
    x = Conv2D(16, (3, 3), activation='relu', padding='same')(x)
    x = MaxPooling2D(pool_size=(2, 2), padding='same')(x)
    flatten_img_features = Flatten()(x)
    x = concatenate([flatten_img_features, flatten_code])
    x = Dense(1024, activation='relu')(x)
    z_mean = Dense(latent_dim)(x)
    z_log_var = Dense(latent_dim)(x)

Код для энкодера со вторым методом добавления метки — после первой свёртки — как дополнительный канал:

def create_conv_cvae2(channels, height, width, code_h, code_w):
    input_img = Input(shape=(channels, height, width))

    input_code = Input(shape=(code_h, code_w))
    flatten_code = Flatten()(input_code)

    latent_dim = 512
    m_height, m_width = int(height/4), int(width/4)

    def add_units_to_conv2d(conv2, units):
        dim1 = K.int_shape(conv2)[2]
        dim2 = K.int_shape(conv2)[3]
        dimc = K.int_shape(units)[1]
        repeat_n = dim1*dim2
        count = int( dim1*dim2 / dimc)

        units_repeat = RepeatVector(count+1)(units)
        #print('K.int_shape(units_repeat): ', K.int_shape(units_repeat))
        units_repeat = Flatten()(units_repeat)
        # cut only needed lehgth of code
        units_repeat = Lambda(lambda x: x[:,:dim1*dim2], output_shape=(dim1*dim2,))(units_repeat)
        units_repeat = Reshape((1, dim1, dim2))(units_repeat)
        return concatenate([conv2, units_repeat], axis=1)

    x = Conv2D(32, (3, 3), activation='relu', padding='same')(input_img)
    x = add_units_to_conv2d(x, flatten_code)
    #print('K.int_shape(x): ', K.int_shape(x)) #  size here: (17, 32, 32)
    x = MaxPooling2D(pool_size=(2, 2), padding='same')(x)
    x = Conv2D(16, (3, 3), activation='relu', padding='same')(x)
    x = MaxPooling2D(pool_size=(2, 2), padding='same')(x)
    x = Flatten()(x)
    x = Dense(1024, activation='relu')(x)
    z_mean = Dense(latent_dim)(x)
    z_log_var = Dense(latent_dim)(x)

Код декодера в обоих случаях совпадает — метка добавляется в самом начале.

    z = Input(shape=(latent_dim, ))
    input_code_d = Input(shape=(code_h, code_w))
    flatten_code_d = Flatten()(input_code_d)
    x = concatenate([z, flatten_code_d])
    x = Dense(1024)(x)
    x = Dense(16*m_height*m_width)(x)
    x = Reshape((16, m_height, m_width))(x)
    x = Conv2D(16, (3, 3), activation='relu', padding='same')(x)
    x = UpSampling2D((2, 2))(x)
    x = Conv2D(32, (3, 3), activation='relu', padding='same')(x)
    x = UpSampling2D((2, 2))(x)
    decoded = Conv2D(channels, (3, 3), activation='sigmoid', padding='same')(x)

Число параметров сети:

1. 4'221'987
2. 3'954'867

Скорость обучения на одну эпоху:

1. 60 сек
2. 63 сек

Результат после 40 эпох обучения:

1. loss: -0.3232 val_loss: -0.3164
2. loss: -0.3245 val_loss: -0.3191

Как видим, второй метод требует меньше памяти для ИНС, даёт лучше результат, но требует чуть больше времени для обучения.

Осталось визуально сравнить результаты работы.

1. Исходное изображение (32х32)
2. Результат работы — первый метод (latent_dim = 64)
3. Результат работы — первый метод (latent_dim = 512)
4. Результат работы — второй метод (latent_dim = 512)

А теперь посмотрим, как выглядит применение переноса стиля для пиццы, когда кодирование пиццы осуществляется с оригинальным рецептом, а декодирование с другим.

i = 0
for label in labels:
    i += 1
    lbls = []
    for j in range(batch_size):
        lbls.append(label)
    lbls = np.array(lbls, dtype=np.float32)
    print(i, lbls.shape)

    stt_imgs = stt.predict([orig_images, orig_labels, lbls], batch_size=batch_size)
    save_images(stt_imgs, dst='temp/cvae_stt', comment='_'+str(i))

Результат работы переноса стиля (второй метод кодирования):

GAN — генеративная cостязательная сеть

Мне не удалось найти устоявшегося русскоязычного названия подобных сетей.
Варианты:

• генеративные соревновательные сети
• порождающие соперничающие сети
• порождающие соревнующиеся сети

Мне больше нравится:

• генеративные cостязательные сети

С теорией работы GAN опять поможет отличная серия статей:

• Автоэнкодеры в Keras, Часть 5: GAN(Generative Adversarial Networks) и tensorflow
• Автоэнкодеры в Keras, часть 6: VAE + GAN

А для более глубокого понимания — свежая статья в блоге ODS: Нейросетевая игра в имитацию

Однако, начав разбираться и пробовать самостоятельно реализовать генеративную нейронную сеть — я столкнулся с некоторыми сложностями. Например, были моменты, когда генератор выдавал по-настоящему психоделические картинки.

Разобраться в реализации помогли разные примеры:

MNIST Generative Adversarial Model in Keras ( mnist_gan.py ),

рекомендации по архитектуре из статьи конца 2015 года от facebook research про DCGAN (Deep Convolutional GAN):

Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks

а так же набор рекомендаций, позволяющий заставить GAN работать:

How to Train a GAN? Tips and tricks to make GANs work.

Конструирование GAN:

def make_trainable(net, val):
    net.trainable = val
    for l in net.layers:
        l.trainable = val

def create_gan(channels, height, width):

    input_img = Input(shape=(channels, height, width))

    m_height, m_width = int(height/8), int(width/8)

    # generator
    z = Input(shape=(latent_dim, ))
    x = Dense(256*m_height*m_width)(z)
    #x = BatchNormalization()(x)
    x = Activation('relu')(x)
    #x = Dropout(0.3)(x)

    x = Reshape((256, m_height, m_width))(x)

    x = Conv2DTranspose(256, kernel_size=(5, 5), strides=(2, 2), padding='same', activation='relu')(x)

    x = Conv2DTranspose(128, kernel_size=(5, 5), strides=(2, 2), padding='same', activation='relu')(x)

    x = Conv2DTranspose(64, kernel_size=(5, 5), strides=(2, 2), padding='same', activation='relu')(x)

    x = Conv2D(channels, (5, 5), padding='same')(x)
    g = Activation('tanh')(x)

    generator = Model(z, g, name='Generator')

    # discriminator
    x = Conv2D(128, (5, 5), padding='same')(input_img)
    #x = BatchNormalization()(x)
    x = LeakyReLU()(x)
    #x = Dropout(0.3)(x)
    x = MaxPooling2D(pool_size=(2, 2), padding='same')(x)
    x = Conv2D(256, (5, 5), padding='same')(x)
    x = LeakyReLU()(x)
    x = MaxPooling2D(pool_size=(2, 2), padding='same')(x)
    x = Conv2D(512, (5, 5), padding='same')(x)
    x = LeakyReLU()(x)
    x = MaxPooling2D(pool_size=(2, 2), padding='same')(x)
    x = Flatten()(x)
    x = Dense(2048)(x)
    x = LeakyReLU()(x)
    x = Dense(1)(x)
    d = Activation('sigmoid')(x)

    discriminator = Model(input_img, d, name='Discriminator')

    gan = Sequential()
    gan.add(generator)
    make_trainable(discriminator, False) #discriminator.trainable = False
    gan.add(discriminator)

    return generator, discriminator, gan

gan_gen, gan_ds, gan = create_gan(channels, height, width)

gan_gen.summary()
gan_ds.summary()
gan.summary()

opt = Adam(lr=1e-3)
gopt = Adam(lr=1e-4)
dopt = Adam(lr=1e-4)

gan_gen.compile(loss='binary_crossentropy', optimizer=gopt)
gan.compile(loss='binary_crossentropy', optimizer=opt)

make_trainable(gan_ds, True)
gan_ds.compile(loss='binary_crossentropy', optimizer=dopt)

Как видим, дискриминатор – это обычный бинарный классификатор, который выдаёт:

1 — для реальных картинок,
0 — для поддельных.

Процедура обучения:

• получаем порцию реальных картинок
• генерируем шум, на базе которого генератор генерирует картинки
• формируем батч для обучения дискриминатора, который состоит из реальных картинок (им присваивается метка 1) и подделок от генератора (метка 0)
• обучаем дискриминатор
• обучаем GAN (в нём обучается генератор, т.к. обучение дискриминатора отключено), подавая на вход шум и ожидая на выходе метку 1.

for epoch in range(epochs):
    print('Epoch {} from {} ...'.format(epoch, epochs))

    n = x_train.shape[0]
    image_batch = x_train[np.random.randint(0, n, size=batch_size),:,:,:]    

    noise_gen = np.random.uniform(-1, 1, size=[batch_size, latent_dim])

    generated_images = gan_gen.predict(noise_gen, batch_size=batch_size)

    if epoch % 10 == 0:
        print('Save gens ...')
        save_images(generated_images)
        gan_gen.save_weights('temp/gan_gen_weights_'+str(height)+'.h5', True)
        gan_ds.save_weights('temp/gan_ds_weights_'+str(height)+'.h5', True)
        # save loss
        df = pd.DataFrame( {'d_loss': d_loss, 'g_loss': g_loss} )
        df.to_csv('temp/gan_loss.csv', index=False)

    x_train2 = np.concatenate( (image_batch, generated_images) )
    y_tr2 = np.zeros( [2*batch_size, 1] )
    y_tr2[:batch_size] = 1

    d_history = gan_ds.train_on_batch(x_train2, y_tr2)
    print('d:', d_history)
    d_loss.append( d_history )

    noise_gen = np.random.uniform(-1, 1, size=[batch_size, latent_dim])
    g_history = gan.train_on_batch(noise_gen, np.ones([batch_size, 1]))
    print('g:', g_history)
    g_loss.append( g_history )

Обратите внимание, что, в отличие от вариационного автоэнкодера, для обучение генератора не используются реальные изображения, а только метка дискриминатора. Т.е. генератор обучается на градиентах ошибки от дискриминатора.

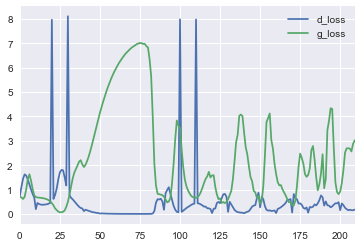
Самое интересное, что название состязательные сети — не для красивого слова — они действительно cостязаются и следить за показаниями loss-ов дискриминатора и генератора даже увлекательно.

Если посмотреть на кривые потерь, то видно, что дискриминатор быстро обучается отличать реальную картинку от первоначального мусора, выдаваемого генератором, но потом кривые начинают колебаться — генератор учится генерировать всё более подходящее изображение.

gif-ка показывающая процесс обучения генератора (32x32) на одной пицце (первая пицца в списке — Двойная пепперони):

Как и ожидалось, результат работы GAN, по сравнению с вариационным энкодером, даёт более чёткое изображение.

CVAE + GAN — условный вариационный автоэнкордер и генеративная cостязательная сеть

Осталось объединить CVAE и GAN вместе, чтобы получить лучшее от обоих сетей. В основе объединения лежит простая идея — декодер VAE выполняет ровно ту же функцию, что и генератор GAN, однако выполняют и обучаются они ей по-разному.

Кроме того, что не до конца понятно — как всё это заставить работать вместе, мне так же не было ясно — как в Keras-е можно применять разные функции потерь. Разобраться в этом вопросе помогли примеры на гитхабе:

> Keras VAEs and GANs

Так, применение разных функций потерь в Keras-е можно реализовать добавлением своего слоя ( Writing your own Keras layers ), в методе call() которого и реализовать требуемую логику рассчёта c последующим вызовом метода add_loss().

Пример:

class DiscriminatorLossLayer(Layer):
    __name__ = 'discriminator_loss_layer'

    def __init__(self, **kwargs):
        self.is_placeholder = True
        super(DiscriminatorLossLayer, self).__init__(**kwargs)

    def lossfun(self, y_real, y_fake_f, y_fake_p):
        y_pos = K.ones_like(y_real)
        y_neg = K.zeros_like(y_real)
        loss_real = keras.metrics.binary_crossentropy(y_pos, y_real)
        loss_fake_f = keras.metrics.binary_crossentropy(y_neg, y_fake_f)
        loss_fake_p = keras.metrics.binary_crossentropy(y_neg, y_fake_p)
        return K.mean(loss_real + loss_fake_f + loss_fake_p)

    def call(self, inputs):
        y_real = inputs[0]
        y_fake_f = inputs[1]
        y_fake_p = inputs[2]
        loss = self.lossfun(y_real, y_fake_f, y_fake_p)
        self.add_loss(loss, inputs=inputs)

        return y_real

gif-ка показывающая процесс обучения (64x64):

Результат работы переноса стиля:

А теперь самое интересное!

Собственно ради чего это всё и затевалось — генерация пиццы по выбранным ингредиентам.

Посмотрим на пиццы с рецептом, состоящим из одного ингредиента (т.е. с кодами от 1 до 27):

Как и следовало ожидать — более-менее смотрятся только пиццы с самыми популярными ингредиентами 24, 20, 17 (томаты, пепперони, моцарелла) — все остальные варианты — это что-то мутное с круглой формой и непонятными серыми пятнами, в которых только при желании можно попытаться что-то угадать.

Заключение

В целом, эксперимент можно признать частично удавшимся. Однако, даже на таком игрушечном примере чувствуется, что пафосное выражение: "данные — это новая нефть" — имеет право на существование, особенно применительно к машинному обучению.
Ведь качество работы приложения на базе машинного обучения, в первую очередь зависит от качества и количества данных.

Генеративные сети — это действительно очень интересно и, думается, что в обозримом будущем мы ещё увидим множество самых различных примеров их применения.

Кстати, возникает хороший вопрос: если права на фотографии принадлежат их создателю, то кому принадлежат права на картинку, которую создаёт нейронная сеть?

Большое спасибо за внимание!

NB. При написании этой статьи — ни одна пицца не пострадала.

Ссылки

• Автоэнкодеры в Keras, Часть 3: Вариационные автоэнкодеры (VAE)
• Автоэнкодеры в Keras, Часть 4: Conditional VAE
• Автоэнкодеры в Keras, Часть 5: GAN(Generative Adversarial Networks) и tensorflow
• Автоэнкодеры в Keras, часть 6: VAE + GAN
• Deep Convolutional GANs (DCGAN): Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks
• How to Train a GAN? Tips and tricks to make GANs work
• Keras VAEs and GANs
• MNIST Generative Adversarial Model in Keras ( mnist_gan.py )
• Generative Adversarial Networks Part 2 — Implementation with Keras 2.0
• Generative Adversarial Networks with Keras
• GAN by Example using Keras on Tensorflow Backend
• Keras implementation of Deep Convolutional Generative Adversarial Networks (DCGAN)
• Генеративные модели от OpenAI
• Нейросетевая игра в имитацию