Насыпав песок на колеблющуюся упругую пластинку, можно увидеть формирование фигур Хладни. Они часто служат примером «естественной красоты» физических явлений, хотя за ними стоит довольно простая физика резонансного возбуждения стоячих волн. И мало кто обращает внимание на любопытную особенность этих фигур: линии на них избегают пересечений, будто их отталкивает некая сила. Давайте попробуем понять, какая же физика скрывается за этим отталкиванием и как она связана с квантовой теорией хаоса.

Стоячие волны

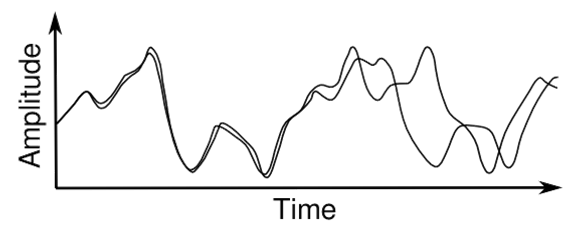
Как мы знаем, упругие тела могут совершать довольно сложные колебания, при которых они сжимаются, растягиваются, изгибаются и скручиваются. Тем не менее, колебания любого упругого тела можно представить как комбинацию накладывающихся друг на друга более простых нормальных колебаний. Вот так выглядят несколько нормальных колебаний простейшего упругого тела – одномерной натянутой струны.

Каждое нормальное колебание представляется стоячей волной, которая, в отличие от бегущей волны, стоит на месте и обладает своим рисунком распределения амплитуд колебаний по пространству. На этом рисунке можно выделить пучности – точки, где амплитуда колебаний достигает максимумов, и узлы – неподвижные точки, в которых амплитуда колебаний равна нулю. Кроме того, каждая такая волна колеблется со своей собственной частотой. В случае струны, как можно заметить, частота колебаний стоячей волны увеличивается с ростом числа узлов и пучностей.


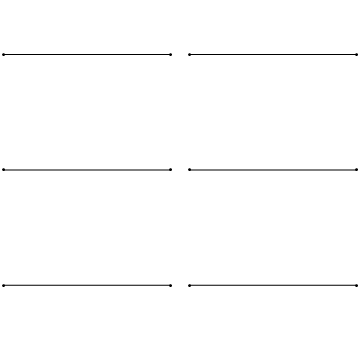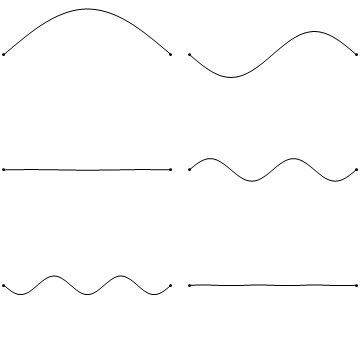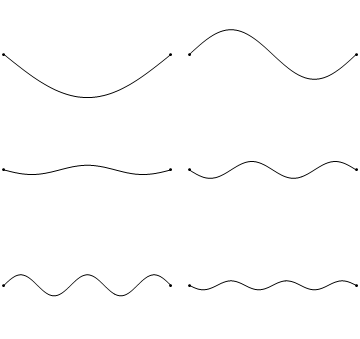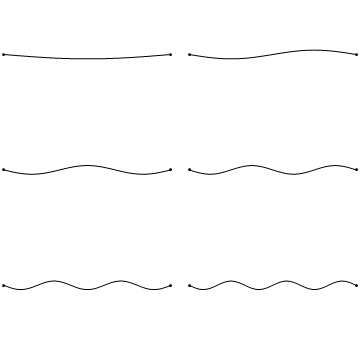
Посмотрим теперь на двумерную систему, примером которой может служить тонкая упругая мембрана, натянутая на жесткую рамку. Нормальные колебания круглой мембраны выглядят сложнее, чем в случае струны, а вместо отдельных точек-узлов имеются узловые линии, вдоль которых мембрана неподвижна.


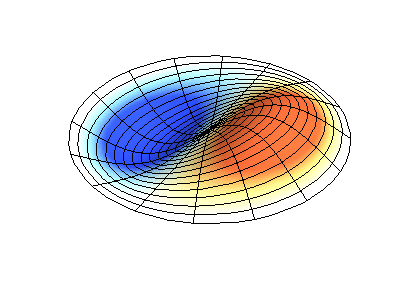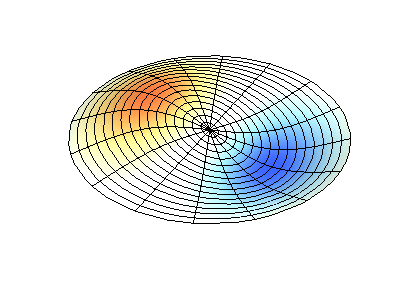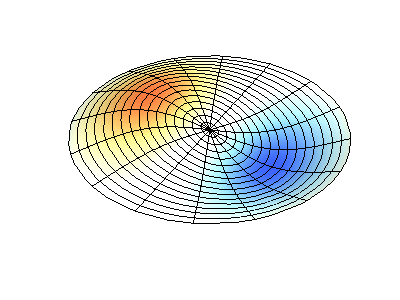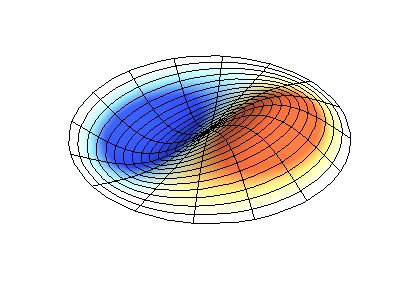
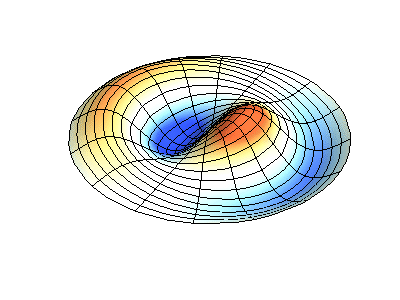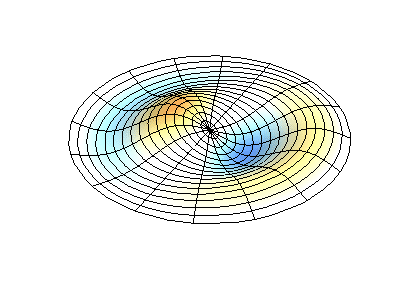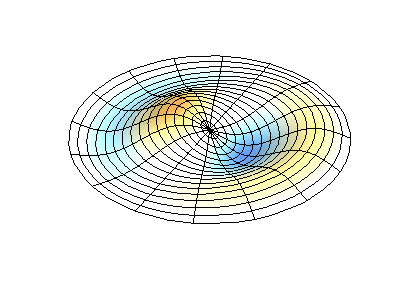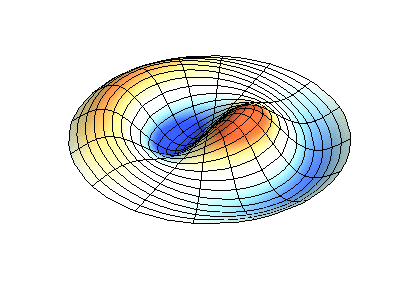
Нормальные колебания круглой мембраны с закрепленными краями. Источник.


Зеленым цветом показаны узловые линии.

У круглой мембраны узловые линии, представляющие собой окружности и отрезки вдоль радиусов, могут пересекаться под прямыми углами. Если же края мембраны имеют произвольную форму, нахождение частот нормальных колебаний и картин их узлов и пучностей превращаются в задачу, решаемую только с помощью компьютера.

Профили амплитуды колебаний стоячих волн на мембранах в форме квадрата с отверстием, снежинки Коха и поверхности котенка.

Уравнения, описывающие колебания тонкой упругой пластинки, отличаются от уравнений колебания мембраны, поскольку пластинка обладает собственной жесткостью, в то время как мембрана мягкая и пружинит лишь за счет натяжения внешними силами. Однако здесь тоже существуют наборы нормальных колебаний, рисунки которых существенным образом зависят от формы границ.

Фигуры Хладни

Как было сказано выше, в общем случае колебания тела представляют собой комбинацию целого набора возбужденных в нем нормальных колебаний. Явление резонанса позволяет выборочно возбудить какое-то одно нужное нам нормальное колебание – для этого следует раскачивать тело при помощи внешней силы с частотой, равной собственной частоте нормального колебания.

На двух видео ниже показана типичная схема получения фигур Хладни: упругая пластинка прикрепляется в центре к генератору механических колебаний, частоту которых плавно увеличивают. Нормальные колебания пластинки со своими картинами узлов и пучностей возбуждаются при резонансном совпадении частоты генератора с собственными частотами этих колебаний (собственные частоты показаны на видео в левом нижнем углу).

Здесь версия этого же видео, на которой частоты нормальных колебаний можно оценить на слух.

А здесь немного красивее.

Картины узлов и пучностей мы видим благодаря тому, что воздушные потоки вблизи колеблющейся пластинки сдувают песчинки к узловым линиям стоячей волны^(*). Таким образом, фигуры Хладни показывают нам картины узловых линий нормальных колебаний упругой пластинки.

Несколько фигур Хладни на верхней деке гитары. Источник.

Еще пример нормальных волн – это стоячие волны на поверхности воды. Они описываются уравнением, отличающимся от уравнений колебания пластинок и мембран, но следуют таким же качественным закономерностям, и с их помощью можно получать аналоги фигур Хладни.

Микрочастицы на поверхности воды в сосудах разной формы. Черная линия показывает масштаб 2 миллиметра. Источник.

Классический хаос

Итак, мы видели, что в случае круглой мембраны узловые линии – теоретически! – замечательно пересекаются, в то же время на фигурах Хладни на квадратных или более сложных пластинках узловые линии избегают пересечений. Чтобы понять причину этих закономерностей, нам придется сделать небольшой экскурс в теорию хаоса.

Классический хаос – это свойство механических систем, заключающееся в чрезвычайно сильной зависимости траектории их движения от изменений начальных условий. Эта зависимость известна также как «эффект бабочки». Яркий пример хаотического поведения можно встретить при попытках предсказания погоды: система уравнений, описывающая движение атмосферы и океанов, не позволяет дать достаточно точные прогнозы на больших временах из-за экспоненциально нарастающих ошибок, обусловленных малыми неточностями исходных данных^(**).

Явление хаоса было открыто и популяризовано метеорологом и математиком Эдвардом Лоренцем, обнаружившим, что два расчета прогноза погоды, начинающиеся с очень близких начальных условий, сначала почти неотличимы друг от друга, но с какого-то момента начинают кардинально расходиться.

Два расчета Эдварда Лоренца, исходящие из близких начальных значений 0.506 и 0.506127. Источник.

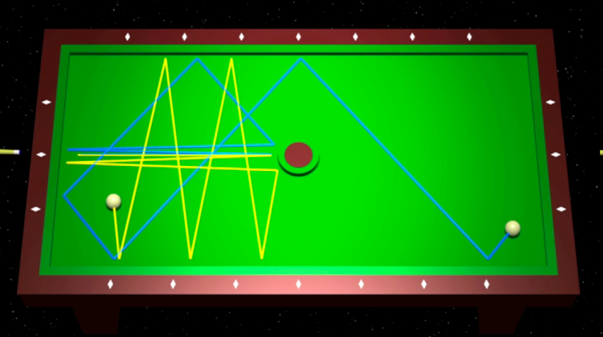
Простейшими системами, на примере которых удобно изучать хаос, являются бильярды – участки плоской поверхности, по которым без трения может катиться шарик, абсолютно упруго отскакивающий от жестких стенок. В хаотических бильярдах траектории движения шарика, имеющие незначительные отличия в самом начале, в дальнейшем существенно расходятся. Пример хаотического бильярда – изображенный ниже бильярд Синая, представляющий собой прямоугольный бильярд с круговым препятствием в центре. Как мы увидим, именно за счет этого препятствия бильярд становится хаотическим.

Две экспоненциально расходящиеся траектории шарика в бильярде Синая. Источник.

Интегрируемые и хаотические системы

Механические системы, не являющиеся хаотическими, называются интегрируемыми, и на примере бильярдов можно наглядно увидеть разницу между интегрируемыми и хаотическими системами.

Прямоугольный и круглый бильярды являются интегрируемыми благодаря своей симметричной форме^(***). Движение шарика в таких бильярдах – это просто комбинация двух независимых периодических движений. В прямоугольном бильярде это движения с отскоками от стенок по горизонтали и по вертикали, а круглом это движение вдоль радиуса и угловое движение по окружности вокруг центра. Такое движение легко просчитываемо и не показывает хаотического поведения.

Траектории движения шарика в интегрируемых бильярдах.

Бильярды более сложной формы, не обладающие столь высокой симметрией, как у круга или прямоугольника, являются хаотическими^(****). Один из них мы видели выше – это бильярд Синая, в котором симметрия прямоугольника разрушается круговым включением в центре. Также часто рассматриваются бильярд «стадион» и бильярд в форме улитки Паскаля. Движение шарика в хаотических бильярдах происходит по весьма запутанным траекториям и не раскладывается на более простые периодические движения.

Траектории движения шарика в хаотических бильярдах «стадион» и «улитка Паскаля».

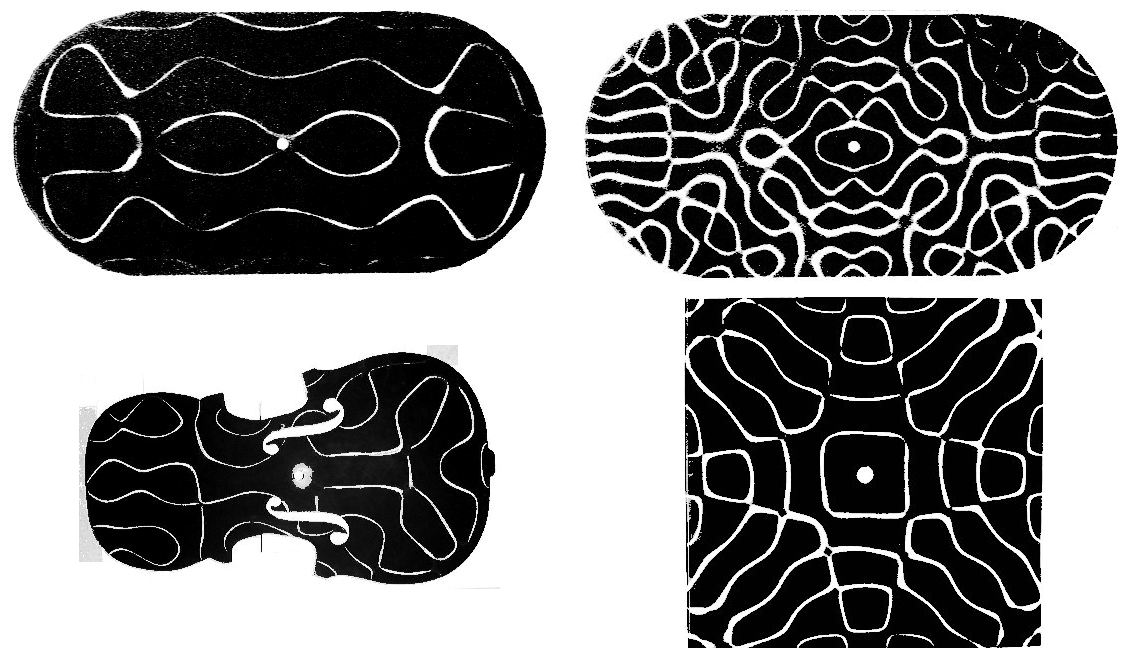
Здесь можно уже догадаться, что наличие пересечений между линиями на фигурах Хладни определяется тем, имеет ли пластинка форму интегрируемого или хаотического бильярда. Это наглядно видно на фотографиях ниже.

Круглые пластинки Хладни, демонстрирующие свойства интегрируемых бильярдов. Источник.

Демонстрирующие свойства хаотических бильярдов пластинки Хладни в форме бильярда «стадион», корпуса скрипки и квадрата, симметрия которого нарушена круглым креплением в центре (аналог бильярда Синая). Источник.

Квантовый хаос

Как же понять, почему наличие пересечений между узловыми линиями обусловлено интегрируемостью бильярда? Для этого нужно обратиться к квантовой теории хаоса, объединяющей теорию хаоса с механикой колебаний и волн. Если в классической механике шарик в бильярде описывается в виде материальной точки, движущейся вдоль определенной траектории, то в квантовой механике его движение описывается как распространение волны, подчиняющейся уравнению Шредингера и отражающейся от стенок бильярда.

Этапы распространения волны в квантовом бильярде. Изначально волна сконцентрирована в импульсе круглой формы и движется слева направо, затем она расплывается и многократно переотражается от стенок. Источник.

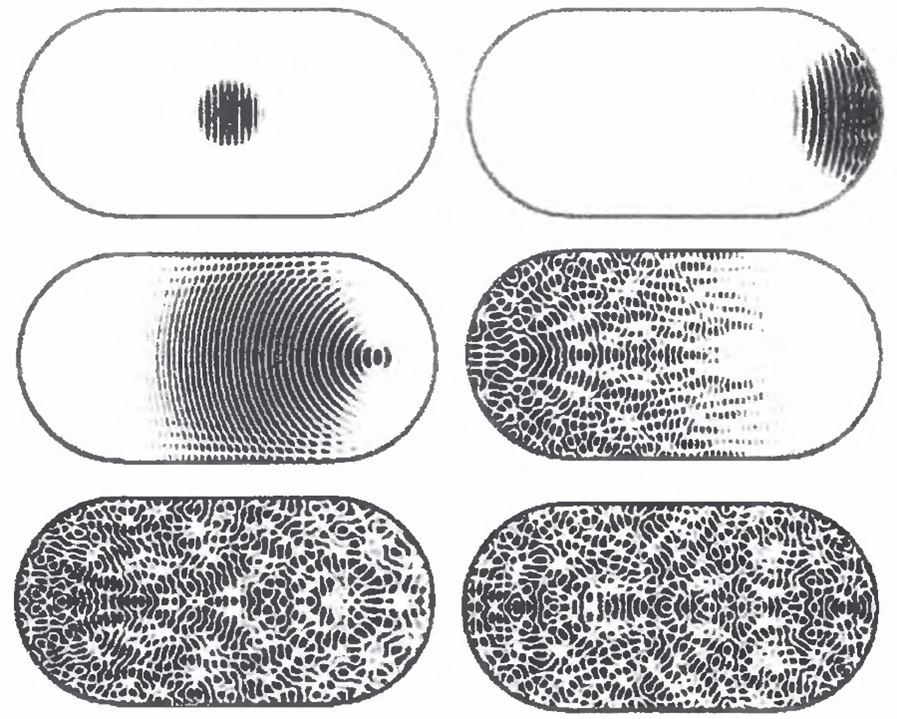
То же самое в виде анимации, но с немного другими начальными условиями.

Как и в случае колебаний мембран и пластинок, описывающее квантовый бильярд уравнение Шредингера позволяет найти нормальные колебания в виде стоячих волн, обладающие характерным рисунком узловых линий и пучностей, индивидуальным для каждого колебания и зависящим от формы границ.

Примеры профилей амплитуд колебаний в стоячих волнах в хаотических квантовых бильярдах «улитка Паскаля» и «стадион».

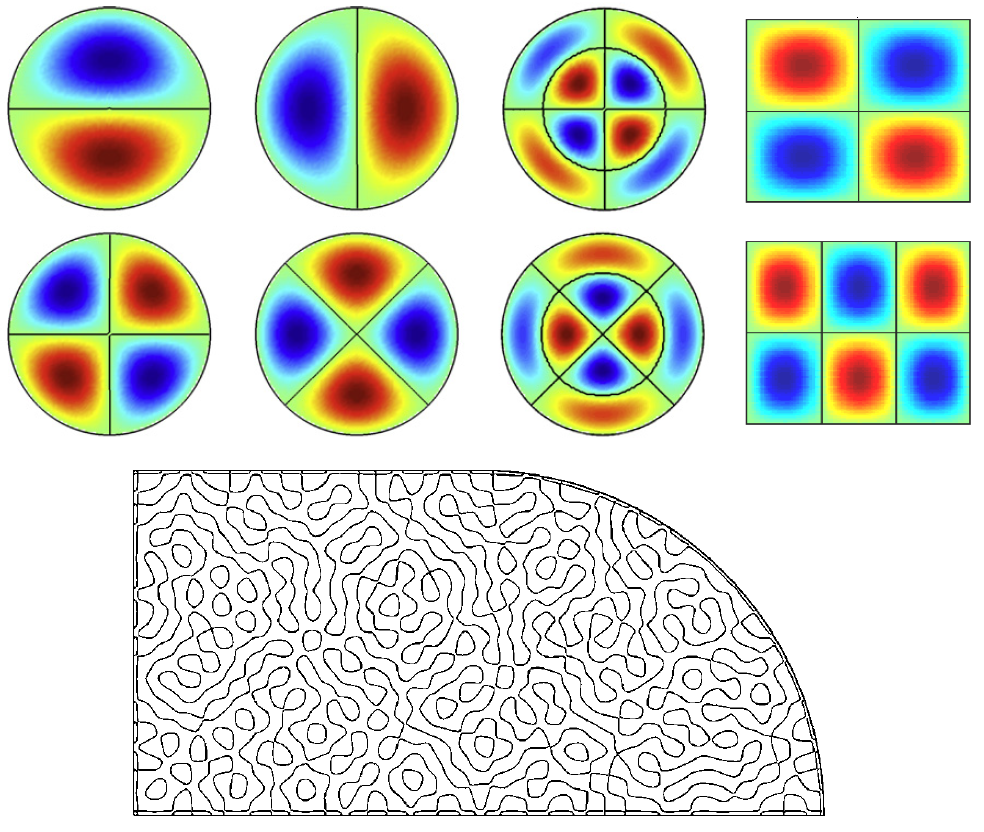
Рисунки стоячих волн в интегрируемых и хаотических квантовых бильярдах качественно отличаются: интегрируемые бильярды показывают симметричные, упорядоченные картины стоячих волн, в то время как в хаотических бильярдах рисунки стоячих волн весьма запутанные и не показывают никаких видимых закономерностей (в конце статьи будет показано, что некоторые интересные закономерности там все-таки существуют).

Амплитуды колебаний в стоячих волнах интегрируемого круглого бильярда (верхний ряд) и хаотического бильярда в форме улитки Паскаля (нижний ряд). Источник.

Причудливые картины нормальных колебаний в хаотических бильярдах иногда служат предметом отдельного исследования. Источник.

Качественное отличие видно и в картинах узловых линий: в случае интегрируемого квантового бильярда мы видим упорядоченные семейства взаимно пересекающихся линий, а в хаотических бильярдах эти линии, как правило, не пересекаются.

Вверху: узловые линии (черные линии между синими и красными областями) стоячих волн интегрируемых – круглого и прямоугольного – бильярдов. Внизу: узловые линии одной из стоячих волн в хаотическом бильярде – четверти бильярда «стадион».

Пересекаться или не пересекаться?

Почему же узловые линии в хаотических бильярдах не пересекаются? В 1976 году математик Карен Уленбек доказала теорему, согласно которой узловые линии стоячих волн квантовых бильярдов, вообще говоря, и не должны пересекаться.

В упрощенном виде это можно показать следующим образом: допустим, что две узловые линии пересекаются в точке (x₀,y₀). Чтобы такое произошло, функция f(x,y), задающая зависимость амплитуды стоячей волны от координат, должна одновременно удовлетворять трем условиям:

1) Она должна быть равна нулю в точке (x₀,y₀), так как эта точка является узловой.
2) Если двигаться из точки (x₀,y₀) в направлении первой узловой линии, то f(x,y) должна оставаться равной нулю.
3) Если двигаться из точки (x₀,y₀) в направлении второй узловой линии, то f(x,y) также должна оставаться равной нулю.


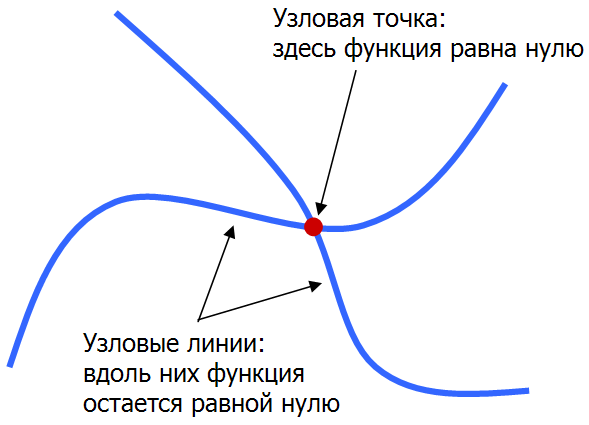
Итого имеем три условия (или три уравнения), наложенные на функцию двух переменных f(x,y). Как мы знаем, одного уравнения недостаточно для полного нахождения двух неизвестных x и y, двух уравнений для этого уже достаточно, а три уравнения – это слишком много. Система трех уравнений для двух неизвестных, вообще говоря, решений иметь не будет, если только нам случайно не повезет. Поэтому точки пересечения узловых линий могут существовать только в порядке исключения.

В интегрируемых бильярдах такие исключения как раз и возникают. Как мы видели выше, их особые свойства – предсказуемость движения, отсутствие хаоса, регулярные рисунки стоячих волн – являются следствием их высокой симметрии. Эта же симметрия обеспечивает и одновременное выполнение трех условий, необходимое для пересечений узловых линий.

Давайте теперь более внимательно посмотрим на примеры фигур Хладни, типичных для интегрируемых и хаотических бильярдов. На рисунке ниже показаны три характерных случая. Слева пластинка имеет форму круга, поэтому соответствующий квантовый бильярд является интегрируемым, и узловые линии пересекаются между собой. В центре пластинка прямоугольная, что тоже соответствует интегрируемой системе, однако круглое крепление в центре слегка нарушает симметрию прямоугольника, поэтому узловые линии пересекаются не везде. Справа показан пример чисто хаотической системы: пластинка в форме четверти бильярда Синая (в верхнем правом углу есть круговой вырез), узловые линии на которой уже не пересекаются.



Таким образом, чем сильнее форма пластинки – с учетом ее крепления – отличается от формы интегрируемого бильярда (такого как круг или прямоугольник), тем меньше на ней пересечений узловых линий.

Получить красивые фигуры Хладни с пересекающимися линиями на круглой пластинке не так-то просто. При возбуждении колебаний с центральным креплением круговая симметрия всей системы запрещает формирование радиальных узловых линий, поэтому мы увидим лишь скучный набор окружностей (эту трудность можно обойти, возбуждая колебания не с центра, а с края пластинки при помощи смычка от скрипки). Если же пластинку закрепить не по центру, фигуры Хладни станут интереснее, но из-за нарушения круговой симметрии система перестанет быть интегрируемой.

Круглая пластинка, крепление по центру.

Круглая пластинка, крепление сдвинуто из центра.

А здесь разные варианты с круглыми и некруглыми пластинками.

Наконец, внимательный читатель может заметить: а я вижу, что иногда узловые линии пересекаются даже на «хаотических» пластинках. Как же так, если их пересечение запрещено теоремой Уленбек?

Во-первых, узловые линии могут избегать пересечения, но перед этим сближаться так сильно, что из-за конечной ширины дорожки песка нам будет казаться, что пересечение есть. Во-вторых, между интегрируемыми и хаотическими системами на самом деле не существует резкой границы.

Узловые линии – они разделяют черные и белые области – в интегрируемом и хаотическом квантовых бильярдах (слева и справа), и в промежуточном псевдоинтегрируемом случае (в центре). В промежуточном случае есть несколько пересечений узловых линий, в то время как в хаотическом случае их нет вовсе. Источник.

В классической теории хаоса этому вопросу посвящена знаменитая теория Колмогорова-Арнольда-Мозера. Она говорит о том, что если слегка нарушить симметрию интегрируемой системы, то она не станет сразу же проявлять хаотическое поведение, а, по большей части, сохранит свое свойство предсказуемости движения. На уровне квантовой теории хаоса и фигур Хладни это проявляется в том, что в некоторых местах пересечения узловых линий сохраняются. Это происходит либо в особо симметричных точках бильярда, либо далеко от источника возмущения, нарушающего симметрию интегрируемой системы.

Что еще?

Чем еще интересна квантовая теория хаоса? Для заинтересованного читателя упомяну о трех дополнительных вопросах, уже не связанных непосредственно с фигурами Хладни.

1) Важное явление, изучаемое этой теорией – универсальность хаотических систем. Подавляющее большинство систем, в которых могут возникать нормальные колебания, являются хаотическими, и все они – независимо от своей физической природы! – подчиняются одинаковым закономерностям. Феномен универсальности, при котором совершенно разные системы описываются одними и теми же формулами, сам по себе очень красив и служит нам напоминанием о математическом единстве физического мира.

Статистика расстояний между соседними частотами нормальных колебаний в хаотических системах разной физической природы, везде описываемая одной и той же универсальной формулой Вигнера-Дайсона. Источник.

2) Рисунки нормальных колебаний хаотических бильярдов обладают интересной особенностью, называемой «квантовыми шрамами». Мы видели, что траектории движения шарика в хаотическом бильярде обычно выглядит весьма запутанными. Но есть и исключения – это периодические орбиты, достаточно простые и короткие замкнутые траектории, вдоль которых шарик совершает периодическое движение. Квантовыми шрамами называются резкие сгущения стоячих волн вдоль периодических орбит.

Квантовые шрамы в бильярде «стадион», идущие вдоль периодических орбит, показанных красными и зелеными линиями. Источник.

3) До сих пор мы говорили о двумерных системах. Если же рассматривать распространение волн в трехмерном пространстве, то здесь тоже могут возникать узловые линии, вдоль которых амплитуда колебаний равна нулю. Особенно важно это при изучении бозе-конденсации и сверхтекучести, где тысячи атомов движутся как единые «волны материи». Анализ структуры узловых линий волн материи в трехмерном пространстве необходим, например, для понимания того, как возникает и развивается квантовая турбулентность в сверхтекучих системах.

Запутанные трехмерные структуры узловых линий стоячих «волн материи» в бозе-конденсате. Источник.

^(*) Если размер частичек, насыпанных на пластинку, достаточно мал, то их будет сдувать уже не к узлам, а к пучностям стоячей волны, как было показано в этой экспериментальной работе.

^(**) Хотя на обывательском уровне слова «хаотичный» и «случайный» часто используются как синонимы, на уровне физики эти понятия существенно отличаются: хаотические системы являются детерминированными – это системы, движение которых описывается строго определенными уравнениями, не подвержено воздействию случайных факторов и потому предопределено начальными условиями. Однако трудность предсказания движения хаотических систем делает их на практике похожими на случайные.

^(***) Еще один пример интегрируемого бильярда – это бильярд в форме эллипса. В этом случае симметрия, делающая его интегрируемым, уже не столь очевидна, как в случае круга и прямоугольника.

^(****) Если выражаться более точно, то принадлежность бильярда к интегрируемым или хаотическим зависит от числа независимых интегралов движения – сохраняющихся с течением времени величин. Интегрируемые бильярды обладают двумя интегралами движения, в двумерной системе этого достаточно для точного аналитического решения уравнений движения. Хаотический бильярд имеет только один интеграл движения – кинетическую энергию шарика.