Введение
Появилось много популярных статей, где рассказывается о квантовой запутанности. Опыты с квантовой запутанностью весьма эффектны, но премиями не отмечены. Почему вот такие интересные для обывателя опыты не представляют интереса для учёных? Популярные статьи рассказывают об удивительных свойствах пар запутанных частиц — воздействие на одну приводит к мгновенному изменению состояния второй. И что же такое скрывается за термином «квантовая телепортация», о которой уже начали говорить, что она происходит со сверхсветовой скоростью. Давайте рассмотрим все это с точки зрения нормальной квантовой механики.
Что получается из квантовой механики
Квантовые частицы может находиться в двух типах состояний, согласно классическому учебнику Ландау и Лифшица — чистом и смешанном. Если частица не взаимодействует с другими квантовыми частицами, она описывается волновой функцией, зависящей только от её координат или импульсов — такое состояние называют чистым. В этом случае волновая функция подчиняется уравнению Шредингера. Возможен другой вариант — частица взаимодействует с другими квантовыми частицами. В этом случае волновая функция относится уже ко всей системе взаимодействующих частиц и зависит от всех их динамических переменных. Если мы интересуемся только одной частицей, то её состояние, как показал Ландау ещё 90 лет назад, можно описать матрицей или оператором плотности. Матрица плотности подчиняется уравнению, аналогичному уравнению Шредингера
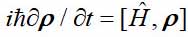
где
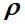— матрица плотности, H — оператор Гамильтона, а скобки обозначают коммутатор.Его вывел Ландау. Любые физические величины, относящиеся к данной частицы, можно выразить через матрицу плотности. Такое состояние называют смешанным. Если у нас есть система взаимодействующих частиц, то каждая из частиц находится в смешанном состоянии. Если частицы разлетелись на большие расстояния, и взаимодействие исчезло, их состояние все равно останется смешанным. Если же каждая из нескольких частиц находятся в чистом состоянии, то волновая функция такой системы есть произведение волновых функций каждой из частиц (если частицы различны. Для одинаковых частиц, бозонов или фермионов, надо составить симметричную или антисимметричную комбинацию см. [1], но об этом позже. Тождественность частиц, фермионы и бозоны – это уже релятивистская квантовая теория.
Запутанным состоянием пары частиц называется такое состояние, в котором имеется постоянная корреляция между физическими величинами, относящимися к разным частицам. Простой и наиболее часто распространенный пример — сохраняется некая суммарная физическая величина, например, полный спин или момент импульса пары. Пара частиц при этом находится в чистом состоянии, но каждая из частиц — в смешанном. Может показаться, что изменение состояния одной частицы сразу скажется на состоянии другой частицы. Даже если они разлетелись далеко и не взаимодействуют, Именно это высказывается в популярных статьях. Это явление уже окрестили квантовой телепортацией, Некоторые малограмотные журналисты даже утверждают, что изменение происходит мгновенно, то есть распространяется быстрее скорости света.
Рассмотрим это с точки зрения квантовой механики, Во-первых, любое воздействие или измерение, меняющее спин или момент импульса только одной частицы, сразу же нарушает закон сохранения суммарной характеристики. Соответствующий оператор не может коммутировать с полным спином или полным моментом импульса. Таким образом, нарушается первоначальная запутанность состояния пары частиц. Спин или момент второй частицы уже нельзя однозначно связать с таковым для первой. Можно рассмотреть эту проблему с другой стороны. После того, как взаимодействие между частицами исчезло, эволюция матрицы плотности каждый из частиц описывается своим уравнением, в которое динамические переменные другой частицы не входят. Поэтому воздействие на одну частицу не будет менять матрицу плотности другой.
Имеется даже теорема Эберхарда [2], которая утверждает, что взаимное влияние двух частиц невозможно обнаружить измерениями. Пусть имеется квантовая система, которая описывается матрицей плотности. И пусть эта система состоит из двух подсистем A и B. Теорема Эберхарда гласит, что никакое измерение наблюдаемых, связанных только с подсистемой A, не влияет на результат измерения любых наблюдаемых, которые связаны только с подсистемой B. Впрочем, доказательство теоремы использует гипотезу редукции волновой функции, которая не доказана ни теоретически, ни экспериментально. Но все эти рассуждения сделаны в рамках нерелятивистской квантовой механики и относятся к различным, не тождественным частицам.
Эти рассуждения не работают в релятивистской теории в случае пары одинаковых частиц. Еще раз напомню, что тождественность или неразличимость частиц – из релятивистской квантовой механики, где число частиц не сохраняется. Однако для медленных частиц мы можем использовать более простой аппарат нерелятивистской квантовой механики, просто учитывая неразличимость частиц. Тогда волновая функция пары должна быть симметричной (для бозонов) или антисимметричной (для фермионов) по отношению к перестановке частиц. Такое требование возникает в релятивистской теории, независимо от скоростей частиц. Именно это требование приводит к дальнодействующим корреляциям пары одинаковых частиц. В принципе протон с электроном тоже могут находиться в запутанном состоянии. Однако если они разойдутся на несколько десятков ангстрем, то взаимодействие с электромагнитными полями и другими частицами разрушит это состояние. Обменное взаимодействие (так называют это явление) действует на макроскопических расстояниях, как показывают эксперименты. Пара частиц, даже разойдясь на метры, остается неразличимой. Если вы проводите измерение, то вы точно не знаете, к какой частице относится измеряемая величина. Вы проводите измерения с парой частиц одновременно. Поэтому все эффектные эксперименты проводились именно с одинаковыми частицами – электронами и фотонами. Строго говоря, это не совсем то запутанное состояние, которое рассматривают в рамках нерелятивистской квантовой механики, но что-то похожее.
Рассмотрим простейший случай – пара одинаковых невзаимодействующих частиц. Если скорости малы, мы можем пользоваться нерелятивистской квантовой механикой с учетом симметрии волновой функции по отношению к перестановке частиц. Пусть волновая функция первой частицы
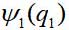, второй частицы — 
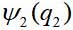, где 
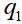и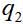 
— динамические переменные первой и второй частиц, в простейшем случае – просто координаты. Тогда волновая функция пары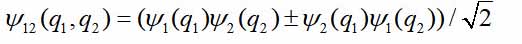 
Знаки + и – относятся к бозонам и фермионам. Предположим, что частицы находятся далеко друг от друга. Тогда
локализованы в удаленных областях 1 и 2 соответственно, то есть вне этих областей они малы. Попробуем вычислить среднее значение какой-нибудь переменной первой частицы, например, координаты. Для простоты можно представить, что в волновые функции входят только координаты. Окажется, что среднее значение координат частицы 1 лежит МЕЖДУ областями 1 и 2, причем оно совпадает со средним значением для частицы 2. Это на самом деле естественно – частицы неразличимы, мы не можем знать, у какой частицы измеряются координаты. Вообще все средние значения у частиц 1 и 2 будут одинаковы. Это значит, что, перемещая область локализации частицы 1 (например, частица локализована внутри дефекта кристаллической решетки, и мы двигаем весь кристалл), мы воздействуем на частицу 2, хотя частицы не взаимодействуют в обычном смысле – через электромагнитное поле, например. Это простой пример релятивистской запутанности. Никакой мгновенной передачи информации из-за этих корреляций между двумя частицами не происходит. Аппарат релятивистской квантовой теории изначально построен так, что события, находящиеся в пространстве-времени по разные стороны светового конуса, не могут влиять друг на друга. Проще говоря, никакой сигнал, никакое воздействие или возмущение не могут распространяться быстрее света. Обе частицы на самом деле являются состоянием одного поля, например, электрон-позитронного. Воздействуя на поле в одной точке (на частицу 1), мы создаем возмущение, которое распространяется подобно волнам на воде. В нерелятивистской квантовой механике скорость света считается бесконечно большой, оттого возникает иллюзия мгновенного изменения.
Ситуация, когда частицы, разнесенные на большие расстояния, остаются связанными в паре, кажется парадоксальной из-за классических представлений о частицах. Надо помнить, что реально существуют не частицы, а поля. То, что мы представляем, как частицы – просто состояния этих полей. Классическое представление о частицах совершенно непригодно в микромире. Сразу же возникают вопросы о размерах, форме, материале и структуре элементарных частиц. На самом деле ситуации, парадоксальные для классического мышления, возникают и с одной частицей. Например, в опыте Штерна-Герлаха атом водорода пролетает через неоднородное магнитное поле, направленное перпендикулярно скорости. Спином ядра можно пренебречь из-за малости ядерного магнетона, пусть изначально спин электрона направлен вдоль скорости.
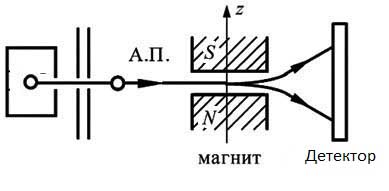
Эволюцию волновой функции атома нетрудно рассчитать. Первоначальный локализованный волновой пакет расщепляется на два одинаковых, летящих симметрично под углом к первоначальному направлению. То есть атом, тяжелая частица, обычно рассматриваемая, как классическая с классической траекторией, расщепился на два волновых пакета, которые могут разлететься на вполне макроскопические расстояния. Заодно замечу – из расчета следует, что даже идеальный эксперимент Штерна-Герлаха не в состоянии измерить спин частицы.
Если детектор связывает атом водорода, например, химически, то «половинки» — два разлетевшихся волновых пакета, собираются в один. Как происходит такая локализация размазанной частицы – отдельно существующая теория, в которой я не разбираюсь. Желающие могут найти обширную литературу по этому вопросу.
Заключение
Возникает вопрос – в чем смысл многочисленных опытов по демонстрации корреляций между частицами на больших расстояниях? Кроме подтверждения квантовой механики, в которой давно уже ни один нормальный физик не сомневается, это эффектная демонстрация, производящая впечатление на публику и дилетантов-чиновников, выделяющих средства на науку (например, разработку квантовых линий связи спонсирует Газпромбанк). Для физики эти дорогостоящие демонстрации ничего не дают, хотя позволяют развивать технику эксперимента.
Литература
1. Ландау, Л. Д., Лифшиц, Е. М. Квантовая механика (нерелятивистская теория). — Издание 3-е, переработанное и дополненное. — М.: Наука, 1974. — 752 с. — («Теоретическая физика», том III).
2. Eberhard, P.H., “Bell’s theorem and the different concepts of nonlocality”, Nuovo Cimento 46B, 392-419 (1978)
Комментарии (37)
Tyusha
15.10.2017 16:47+4Тождественность частиц, фермионы и бозоны – это уже релятивистская квантовая теория
Еще раз напомню, что тождественность или неразличимость частиц – из релятивистской квантовой механики, где число частиц не сохраняется.
Здесь вы неправы. Квантовая статистика, подразумевающая тождественность, спокойно себе существует без квантовой теории поля. То же касается фермионов и бозонов. Им не нужна релятивистская теория.
Что появляется нового в релятивисткой квантовой физике и чего нет в обычной квантовой механике так это непостоянство числа частиц.
ring1956 Автор
18.10.2017 01:11Как вы докажете теорему Паули без аппарата релятивистской теории, где число частиц не сохраняется? Неразличимость частиц в нерелятивистской теории постулируется. а вот в релятивистской естественно следует из того, что частицы — состояния одного и того же поля. То, что в нерелятивистской теории постулируется, в релятивистской возникает естественным образом. И неразличимость тоже.
diversenok
15.10.2017 16:58+4Знаете, вы так людей ещё больше запутаете. Вот пишите вы такие слова как «спин», «коммутатор», «матрица плотности», «смешанное состояние». А объяснять их кто будет? Или расчёт на аудиторию, уже знакомую с этими понятиями? Да и монолитный текст — плохая идея.
Желающим разобраться рекомендую почитать Леонарда Сасскинда «Квантовая механика. Теоретический минимум». Эта книга рассчитана на широкий круг читателей и ставит своей целью объяснить подобные вещи максимально понятно.
Tyusha
15.10.2017 17:26+3ring1956 замахнулся на слишком многое в таком коротком тексте. Квантовая запутанность — непростая тема, поэтому её лучше обсуждать в «дистиллированном» виде. А тут и тождественность частиц, и обменное взаимодействие, и симметризация/анитисимметризация волновый функции, и Штерн с Герлахом. Стоит сказать, что это вообще не имеет отношения к запутанности.
Сейчас всякие квантовые компьютеры и телепортации реализуют на одинаковых частицах. Но скажу вам по секрету, запутывать не обязательно частицы одного сорта!ring1956 Автор
18.10.2017 11:39Сейчас всякие квантовые компьютеры и телепортации реализуют на одинаковых частицах. Но скажу вам по секрету, запутывать не обязательно частицы одного сорта! Я вижу, что статьи Вы вообще не прочитали — я это писал несколько раз. И не по секрету.
«Стоит сказать, что это вообще не имеет отношения к запутанности.» — Я не вижу возражений по существу. Статья качественно и достаточно просто, насколько это возможно, объясняет известные эксперименты с парой одинаковых частиц на больших расстояниях — имеющиеся научные статьи гораздо сложнее и заполнены сложной математикой. Если Вы считаете, что эти опыты не имеют отношения к запутанности, как Вы ее понимаете — дайте свое определение. Пока непонятен предмет возражений, спорить не о чем.
WinPooh73
15.10.2017 19:21Ещё могу порекомендовать книгу Николя Жизана "Квантовая случайность". Она популярно, но достаточно детально, разъясняет эксперименты по парадоксу ЭПР и неравенству Белла.
ring1956 Автор
18.10.2017 12:38Или расчёт на аудиторию, уже знакомую с этими понятиями?
Да, конечно. Рассчитано на студентов, освоивших нерелятивистскую квантовую механику. Тем, кто не знаком с квантовой механикой, читать бесполезно. Кто хочет изучить — пусть берется за учебники. Объяснять могут на лекциях целый семестр — здесь не университет. Существующие разъяснения экспериментов меня совершенно не устроили, авторы увлекаются наукообразием и загромождают статьи математическими формулами без необходимости, не разъясняя физические основы. Для меня образцом был Я.Б. Зельдович, умевший просто изложить решение, не отвлекаясь на долгий расчет коэффициентов порядка единицы. Хотя он был выдающийся математик и вполне мог это сделать. Ландау также умел просто и без лишней математики изложить суть и того же требовал от других.
Tyusha
15.10.2017 17:03+4Аппарат релятивистской квантовой теории изначально построен так, что события, находящиеся в пространстве-времени по разные стороны светового конуса, не могут влиять друг на друга.
Э-э-э… А вот как раз и нет, и в этом вся мощь квантовой теории поля (КТП). Аппарат КТП как раз «не знает» о существовании светового конуса (ну или почти не знает). При вычислении пропагаторов частиц, собтвенно энергетических функций, а также вершинных частей приходится вести интегрирование по всему пространству, не взирая на световой конус, и таким образом ограничения причинности!
Вернее, вычисление как правило ведут в импульсном пространстве, при этом не связывая себя дисперсионным отношением E2 — p2 = m2, что как раз и означает игнорирование светового конуса.
Как вы понимаете, все квантовые эффекты в теории поля не обходятся без участия промежуточных виртуальных частиц. А виртуальные частицы не могут появиться, если вы связаны световым конусом. Так что вы неправы.
Добавлю. Вы же не ставите никаких ограничений на область интегрирования при вычислении фейнмановских континуальных интегралов. Получается, что частица при вычислении амплитуды перехода D(x1, x2) мечется по всему пространству-времени, не обращая внимание, куда она «летит»: в прошлое, в будущее, со сверхсветовой скорость или нет. Другое дело, что основной вклад в интеграл для реальных частиц дают только траектории, соответствующие классическому движению. В то время как другие траектории, нарушающие световой конус, вносят лишь радиационные поправки.
vassabi
16.10.2017 00:19Вы же не ставите никаких ограничений на область интегрирования при вычислении фейнмановских континуальных интегралов. Получается, что частица при вычислении амплитуды перехода D(x1, x2) мечется по всему пространству-времени, не обращая внимание, куда она «летит»: в прошлое, в будущее, со сверхсветовой скорость или нет.
у меня нет знакомых физиков, поэтому спрошу у вас: а есть у физиков понимание смысла этих формул или нет? Или их просто применяют, потому что "ответ сходится"?
(как там у классиков в "Обитаемом Острове": "о чисто абстрактной математической теории, рассматривавшей Мир иначе. Теория [..] получила математическую стройность трудами гениальных математиков прошлого века, но так и осталась чисто абстрактной, хотя, как и большинство абстрактных теорий, нашла себе наконец практическое применение – совсем недавно, когда были созданы сверхдальнобойные баллистические снаряды." )
Ведь, если так — это, значит, если будет новые формулы, дающие такой же результат, как у экспериментов, но с меньшим количеством вычислений чем раньше, то все перебегут считать по ним, забросив старые, "подкреплённые теорией".
Tyusha
16.10.2017 00:43Вопрос философский. Мне ближе позиция «потому что ответ сходится». Не существует какого-то уравнения единого поля. Природа об этом ничего не знает. Она такая, какая есть. Мы пытаем описать её и предсказать её теми средствами, которыми располагаем. Можно описывать просто словами, но это бедный язык, он не позволяет установить всё многообразие связей явлений природы друг с другом.
Язык математики предоставляет более широкие возможности. Мы подбираем ту математическую конструкцию (теорию), которая демонстрирует такие же (правильнее будет сказать: похожие) взаимосвязи, какие мы наблюдаем и интерпретируем в эксперименте.
«Победителей не судят». Если «ответ сходится», вернее до тех пор пока ответ сходится, мы пользуемся той или иной теорией. Для меня совершенно неважно насколько мы можем понять и осмыслить физическую теорию. Такое осмысление помогает интуиции в поиске, но оно на мой взгляд совсем не обязательно. «Заткнись и считай», — грубо, но ёмко выразился по поводу понимания квантовой механики Дэвид Мервин.vassabi
16.10.2017 13:22«Заткнись и считай», — грубо, но ёмко выразился по поводу понимания квантовой механики Дэвид Мервин.
ясно.
Наверно я оптимист, но я уверен, что математики придумают еще новых способов справиться со сложностью формул (типа "эти ваши шесть гамильтонианов в 4хмерном пространстве — всего лишь один мой линейный оператор в 144-х мерном пространстве, так что я вместо шести формул пишу одну"), чтобы машины считали, а человек — думал о физике.
ring1956 Автор
18.10.2017 10:48Э-э-э… А вот как раз и нет, и в этом вся мощь квантовой теории поля (КТП). Аппарат КТП как раз «не знает» о существовании светового конуса (ну или почти не знает). При вычислении пропагаторов частиц, собтвенно энергетических функций, а также вершинных частей приходится вести интегрирование по всему пространству, не взирая на световой конус, и таким образом ограничения причинности!
Я не понял, вы действительно утверждаете, что релятивистская квантовая теория допускает распространение сигналов быстрее света? Релятивистская квантовая теория построена на преобразованиях Лоренца-Пуанкаре (в том числе). Все уравнения сохраняют свой вид при этих преобразованиях. Преобразования Лоренца не допускают систему отсчета, двигающуюся быстрее света. Потому никакие сигналы, никакие волны не могут распространяться быстрее света. Для этого не надо привлекать никаких интегралов по траекториям — это уже математика, основанная также и на релятивистской инвариантности. Если у Вас есть какие-то возражения против этого — изложите ясно. Я ни про какие виртуальные частицы и вычисление пропагаторов не писал — давайте не уходить от предмета статьи.Tyusha
18.10.2017 15:40Наблюдаемые эффекты распространения излучения и частиц, разумеется не превышают скорость света. Но это относится только в реальным концам фейнмановских диаграмм.
ring1956 Автор
18.10.2017 19:54Тогда для чего вы столько написали? Нагромоздили столько всякой всячины, не имеющей никакого отношения к делу, чтобы в конце сказать, что вы согласны с тем, что написано в статье. Там ведь рассматриваются именно опыты.
askv
15.10.2017 17:48Когда одеваешь один носок на левую ногу, второй автоматически мгновенно становится правым. Это и есть квантовая запутанность...
IvanKor2017
15.10.2017 17:58-6Например, в опыте Штерна-Герлаха
Как и во многих других опытах, до этого, наглядно видно что вещество состоит из магнитных моноплей и продвигаемая тогда концепция атома терпела очередной, который по счету крах.
Пришлось изрядно выкручиваться для спасения концепции атома, поэтому наряду с зарядом и массой был введен спин. И было объявлено что в макромире аналога спина нету.
Вот до чего намудрили, если отрицать то что видно глазами и причем однозначно.
Но важно не то что видят глаза, важна концепция, типа Земля плоская.
Dr_Dash
15.10.2017 19:55Вижу вы разбираетесь в этом разделе физики, и хочу воспользоваться ситуацией и поинтересоваться: одиночный фотон обладает и волновыми и корпускулярными свойствами. А как выглядит волна-фотон, она подобна кругам на воде(точнее сфера), или это некоторый солитон, движущийся в определённом направлении(с учётом неопределённости конечно)?
Tyusha
15.10.2017 21:03+1Сразу скажу, что да, одиночный фотон обладает корпускулярными и волновыми свойствами. Однако на вторую часть вопроса ответить не так просто. Получится, боюсь, длинно.
Как квантуется свободное электромагнитное поле. Раскладываем его на базисные моды: как правило, это бесконечные плоские волны всех возможных направлений. Затем «единичная» амплитуда каждой моды объявляется фотоном с энергией ??. Если амплитуда большая — это означает много одинаковых когерентных фотонов.
Но разложение на плоские волны это всего лишь одно из возможных разложений. Оно удобно тем, что каждая мода имеет строго определённую энергию и импульс. В такой форме все квантовые операторы записываются максимально просто, например, энергия (гамильтониан) получается просто суммой количества «фотонов» каждой моды, умноженного на энергию моды.
Ничего не мешает взять другое разложение, пример по сферическим модам с функциями Бесселя в радиальном направлении — те самые «круги на воде», о которых вы спрашиваете. Такие моды будут по прежнему иметь фиксированную (определённую в квантовом смысле энергию), но уже с нулевым интегральным импульсом. Зато у фотонов появится определённый орбитальный момент 1, 2,… 5,… 25.
Можно взять ещё более экзотические разложения. Хотите по солитонам — нет проблем. Матан разрешает, лишь бы система функций, по которой ведётся разложение была полна. При этом может оказаться, что такие моды не имеют строго определённой энергии (та, которая ??). Именно поэтому так обычно не делают. В таких базисах работать не удобно. Матрицы квантовые операторов в них оказываются сложны (недиагональны, например).
Теперь представьте, как мы регистрируем фотон. Пусть у нас есть фотоумножитель — классический прибор. Что мы имеем на выходе: чик, прилетел фотон, энергия такая-то. Всё. Прикол в том, что мы не знаем, какую именно моду мы зафиксировали, т.к. сказать изъяли из электромагнитного поля. Это был фотон «плоская волна», фотон «солитон» или фотон имени Бесселя? Более того, этого узнать нельзя. Произошёл коллапс волновой функции одиночного фотона, и какой она была «до», ничего сказать нельзя.
То же относится и к «форме» волны других частиц, например, электронов. Можно выбирать какие угодно базисы и строить на этом всю квантовую электродинамику, результат будет тем же. Взаимодействие с фотоном описывается членом ?*A?. С которым обычно работают в импульсном представлении, поэтому удобно в качестве мод частиц взять плоские волны. Но это необязательно, хотите вычислительных неприятностей — берите базис какой хотите.Dr_Dash
15.10.2017 22:16Неплохое введение, спасибо. Я упомянул солитон не в качестве базиса, неудачно выразился, а в качестве иллюстрации к вопросу, с чем можно сравнить одиночный фотон, иными словами: одиночный фотон он летит как радиоволна с очень короткой длительностью, во все стороны, или он летит в каком-то одном направлении?
Tyusha
15.10.2017 22:30Я же написала, что мы не знаем, что такое фотон. Вернее, что именно мы поймали. Это в том числе зависит от модели детектора, как именно он взаимодействует с электромагнитным полем. Попробую ещё раз зайти, немного по-другому.
Есть ящик в котором плещется электромагнитное поле. Какова его конфигурация, в смысле зависимости E(x,y,z) мы не знаем, и никто не знает. Она неопредлённая в квантовом смысле слова. В процедуре квантования поля «значение (форма) поля» это всё равно что «координата» в случае обычного квантования движения частицы.
Кто-то может сказать в ящике находится N фотонов «плоских волн» с импульсом, а другой с таким же правом может заявить: нифига, там M «сферических» стоячих фотонов. Но до тех пор, пока мы их не пересчитали (наблюли) достоверно ничего сказать нельзя. И вот начинаем считать, ловим их по одному. Вопрос, как и чем именно ловим. И тут есть сложный (положа руку на сердце, не решённый) момент, т.к. всё зависит от модели детектора. Это именно то промежуточное звено между квантовой системой и классическим прибором. Кроме того, прибор оказывает влияние на систему. Т.е. по сути это неэквивалетные системы пересчёта фотонов.
NIN
16.10.2017 20:41Стоит добавить, что строгая определенность энергии фотона означает, что на его излучение потребуется бесконечное количество времени. Т.е. одиночных фотонов в природе не существует, а атомы излучают «однофотонные пакеты» конечной длительности и с неопределенной энергией. Хотя именно такие пакеты повсеместно называются «одиночными фотонами».
ring1956 Автор
18.10.2017 11:56Вот это действительно грамотно написано. Но есть и другое определение фотона в учебнике Ахиезера и Берестецкого «Квантовая электродинамика», под которое подпадают конечные импульсы света. Но прежде всего надо указать, что координатной волновой функции для фотона не существует, поэтому называть фотон частицей не следует.
ring1956 Автор
18.10.2017 11:52+1Вижу вы разбираетесь в этом разделе физики, и хочу воспользоваться ситуацией и поинтересоваться:
Я бы не рекомендовал изучать такой сложный предмет по комментариям на популярном сайте. Они только внесут путаницу в мозги, и запутанность будет уже там. Здесь нет больших ученых, они читают лекции в университетах, вот по ним и надо изучать предмет. Могу порекомендовать Займана «Введение в квантовую теорию». Когда человек берется в одном комментарии объяснить профану такой сложный вопрос, это либо гений (такими способностями обладал, например, Я.Б. Зельдович), либо полузнайка. прочитавший пару книг и мало что понимающий. Все профессора, у которых я учился, отсылали к учебникам и лекциям. И правильно. Полузнание хуже незнания.Dr_Dash
19.10.2017 07:32Во первых мы здесь профаны, но не конченные, во вторых: полузнание в моём случае это модель Бора, без КЭД. Думаю не только в моём, потому что так мы (обычные радиоэлектронщики) проходили физику в школе+вузе. Но теперь я хотя бы немного представляю насколько отличается электродинамика от квантовой электродинамики, границы применимости так сказать.
IvanKor2017
15.10.2017 22:39-1Вот «фотоны». Длину плеч диполя каждый может выбрать сам, 1 метр или десяток или…
Реальных фотонов не существует в природе, ибо невозможна система излучения ЭМВ которая бы излучила одинокий шарик-фотон с волновыми свойствами. Те кто выдумывали фотоны, обыкновенные фантазеры, не знающие элементарных основ радиотехники.diversenok
15.10.2017 23:38+1А что насчёт излучения из гамма диапазона? Но это ещё ладно, мне особенно хотелось бы услышать комментарий про фотоэффект исходя из такой, чисто волновой, трактовки света. Сдаётся мне, это будет непросто.
vassabi
15.10.2017 23:59имхо, это работает как радио — та частота, которая в резонансе с материалом, та и делает эффект.
diversenok
16.10.2017 10:43Фотоэффект это не только сам факт испускания электронов под действием света, это ещё и три экспериментальные закономерности, две из которых как-раз таки совершенно не удалось объяснить исходя из чисто волнового подхода.
vassabi
16.10.2017 13:17хмм… наверно у меня "в голове" неправильные волны и электроны — они сразу квантовые, так что я не замечаю этой "неудачи объяснить" %)
Dr_Dash
16.10.2017 06:51это «неквантовые» фотоны, Максвелловские так сказать. Оказывается КЭД очень сильно отличается от электродинамики к которой мы привыкли. Начал читать Интересно, в качестве детектива пойдёт )
Tyusha
Ландау конечно гений, но вряд ли он в 9 лет обобщил ещё не открытое на тот момент уравнение Шрёдингера.
qbertych
Вы бы хоть википедию открыли и список премий Алана Аспе посмотрели.
А еще вы неверно вводите смешанные состояния. По-вашему состояние двух частиц |11> — смешанное?
А еще вы неверно вводите квантовую телепортацию (да вы ее и не вводите даже).
В принципе, после этого (и нулевой популярности материала) читать дальше становится бессмысленно.
P.S. Но то, что за два года вы хоть немного научились отличать смешанные состояния от запутанных, не может не радовать ;).
ring1956 Автор
Смешанное состояние двух частиц я ввожу по Ландау. У Вас другая физика — добро пожаловать. Квантовую телепортацию я не ввожу — ее ввели журналисты. Определение запутанности взял из известных обзоров, чтобы не ошибиться. Например,
Н.В.Никитин «Распутываем запутанную квантовую механику:
как мы понимаем неравенства Белла 52 года спустя.» Научный семинар по ядерной физике НИИЯФ МГУ. 18.10.2016
Да, я немного недопонимал всю ту путаницу, что развели вокруг довольно простой вещи (самое главное — зачем?), но вроде бы ясно показал, что известные и популярные эксперименты относятся к несколько другому явлению, отсутствующему в нерелятивистской теории. Без фермионов и бозонов не обойтись.
ring1956 Автор
Отвлекаясь от предмета, должен заметить — такой стиль общения характерен сейчас для студентов на начальном этапе изучения теоретической физики. Для них не существует сомнений и проблем, нобель ждет лет через дцать, а пока хорошо бы заиметь повышенную стипендию.
WinPooh73
Возможно, имеется в виду Эдмунд Ландау, или кто-то ещё из однофамильцев Льва Давыдовича.
ring1956 Автор
Статья 1927 года. Виноват, всего 90 лет прошло. Исправлю