Данный текст будет являться одной из переписанных глав для учебного пособия по защите информации кафедры радиотехники и систем управления МФТИ (ГУ). Полностью учебник доступен на github (см. также draft releases). На хабре я же планирую выкладывать новые «большие» куски, во-первых, чтобы собрать полезные комментарии и замечания, во-вторых, дать сообществу больше обзорного материала по полезным и интересным темам.

Задача распространения ключей является одной из множества задач построения надёжной сети общения многих абонентов. Задача состоит в получении в нужный момент времени двумя легальными абонентами сети секретного сессионного ключа шифрования (и аутентификации сообщений). Хорошим решением данной задачи будем считать такой протокол распространения ключей, который удовлетворяет следующим условиям.

• В результате работы протокола должен между двумя абонентами должны быть сформирован секретный сессионный ключ.
• Успешное окончание работы протокола распространение ключей должно означать успешную взаимную аутентификацию абонентов. Не должно быть такого, что протокол успешно завершился с точки зрения одной из сторон, а вторая сторона при этом представлена злоумышленником.
• К участию в работе протокола должны допускаться только легальные пользователи сети. Внешний пользователь не должен иметь возможность получить общий сессионный ключ с кем-либо из абонентов.
• Добавление нового абонента в сеть (или исключение из неё) не должно требовать уведомления всех участников сети.

Последнее требование сразу исключает такие варианты протоколов, в которых каждый из абонентов знал бы некоторый мастер-ключ общения с любым другим участником. Данные варианты плохи тем, что с ростом системы количество пар мастер-ключей «абонент-абонент» растёт как квадрат от количества участников. Поэтому большая часть рассматриваемых решений состоит в том, что в сети выделяется один или несколько доверенных центров T (Trent, от англ. trust), которые как раз и владеют информацией о всех легальных участниках сети и их ключах. Они же будут явно или неявно выступать одним из участников протоколов по формированию сеансовых ключей.


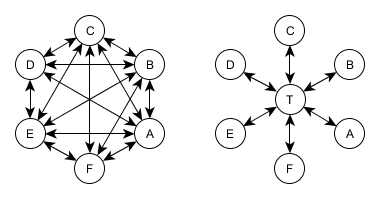
Варианты сетей без выделенного доверенного центра и с выделенным доверенным центром T

Важным моментом при анализе решений данной задачи является то, что сессионные ключи, вырабатываемые в конкретный момент времени, являются менее надёжными, чем мастер-ключи, используемые для генерации сессионных. В частности, нужно предполагать, что хотя злоумышленник не может получить сессионный ключ во время общения абонентов, он может сделать это по прошествии некоторого времени (дни, недели, месяцы). И хотя знание этого сессионного ключа поможет злоумышленнику расшифровать старые сообщения, он не должен иметь возможность организовать новую сессию с использованием уже известного ему сессионного ключа.

Симметричные протоколы

К симметричным будем относить протоколы, которые используют примитивы только классической криптографии на секретных ключах. К таким относятся уже известные блочные шифры, криптографически стойкие генераторы псевдослучайных чисел (КСГПСЧ) и хэш-функции.

При рассмотрении протоколов будем использовать следующие обозначения.

• Alice, Bob — легальные абоненты сети, для которых формируется общий сеансовый ключ. Алиса является инициатором.
• Trent — доверенный центр сети.
• $$, $$ — некоторые идентификаторы легальных абонентов Алисы и Боба соответственно.
• $$, $$ — результат шифрования некоторого блока данных с использованием секретных ключей легальных абонентов сети Алисы и Боба соответственно. Такое шифрование могу осуществить либо сами легальные абоненты, либо доверенный центр, которому известны все секретные ключи.
• $$, $$, $$ — случайные числа, генерируемые Алисой, Бобом и Трентом соответственно.
• $$, $$, $$ — метки времени, генерируемые Алисой, Бобом и Трентом соответственно.
• $$ — секретный сеансовый ключ, получение которого и является одной из целью протоколов.

Протокол Wide-Mouth Frog

Протокол Wide-Mouth Frog является, возможно, самым простым протоколом с доверенным центром. Его автором считается Майкл Бэрроуз (1989 год, англ. Michael Burrows). Протокол состоит из следующих шагов.

1. Алиса генерирует новый сеансовый ключ $$ и отправляет его вместе с меткой времени, идентификатором Боба и своим незашифрованным идентификатором доверенному центру:
   

   $$

2. Доверенный центр, используя полученный незашифрованный идентификатор $$, находит у себя в базе данных легальных абонентов секретный ключ Алисы и расшифровывает им пакет данных. Проверяет метку времени (что пакет не очень старый). Далее он отправляет похожий пакет данных Бобу, зашифрованный его секретным ключом:
   

   $$

   
   Боб, кроме расшифрования пакета, также проверяет метку времени доверенного центра.

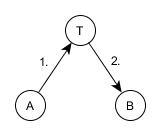
Схема взаимодействия абонентов и довереного центра в протоколе Wide-Mouth Frog

По окончании протокола у Алисы и Боба есть общий сеансовый ключ $$.

У данного протокола множество недостатков.

• Генератором ключа является инициирующий абонент. Если предположить, что Боб — это сервер, предоставляющий некоторый сервис, а Алиса — это тонкий клиент, запрашивающий данный сервис, получается, что задача генерации надёжного сессионного ключа взваливается на плечи абонента с наименьшими мощностями.
• В протоколе общение с вызываемым абонентом происходит через доверенный центр. Как следствие, второй абонент может стать мишенью для DDOS-атаки с отражением (англ. distributed denial-of-service attack), когда злоумышленник будет посылать пакеты на доверенный центр, а тот формировать новые пакеты и посылать их абоненту. Если абонент подключён к нескольким сетям (с несколькими доверенными центрами), это позволит злоумышленнику вывести абонента из строя. Хотя защититься от подобной атаки достаточно просто, настроив соответствующим образом доверенный центр.

Однако самый серьёзные проблемы состоят в возможности применения следующих атак.

В 1995 году Рос Андерсон и Роджер Нидхем (англ. Ross Anderson, Roger Needham) предложили вариант атаки на протокол, при котором злоумышленник (Ева) может бесконечно продлевать срок действия конкретного сеансового ключа. Идея атаки в том, что после окончания протокола злоумышленник будет посылать доверенному центру назад его же пакеты, дополняя их идентификаторами якобы инициирующего абонента.

1. $$
2. $$
3. $$
4. $$
5. $$
6. $$
7. Повторять шаги 3 и 5, пока не пройдёт время, нужное для расшифровки $$.

С точки зрения доверенного центра шаги 1, 3 и 5 являются корректными пакетами, инициирующие общение абонентов между собой. Метки времени в них корректны (если Ева будет успевать вовремя эти пакеты посылать). С точки зрения легальных абонентов каждый из пакетов является приглашением другого абонента начать общение. В результате произойдёт две вещи:

• Каждый из абонентов будет уверен, что закончился протокол создания нового сеансового ключа, что второй абонент успешно аутентифицировал себя перед доверенным центром. И что для установления следующего сеанса связи будет использоваться новый (на самом деле — старый) ключ $$.
• После того, как пройдёт время, нужное злоумышленнику Еве для взлома сеансового ключа $$, Ева сможет и читать всю переписку, проходящую между абонентами, и успешно выдавать себя за обоих из абонентов.

Вторая атака 1997 года Гэвина Лоу (англ. Gavin Lowe) проще в реализации. В результате этой атаки Боб уверен, что Алиса аутентифицировала себя перед доверенным центром и хочет начать второй сеанс общения. Что, конечно, не является правдой, так как второй сеанс инициирован злоумышленником.

1. $$
2. $$
3. $$

В той же работе Лоу предложил модификацию протокола, вводящую явную взаимную аутентификацию абонентов с помощью случайной метки $$ и проверки, что Алиса может расшифровать пакет с меткой, зашифрованной общим сеансовым ключом абонентов $$. Однако данная модификация приводит к тому, что протокол теряет своё самое главное преимущество перед другими протоколами — простоту.

1. $$
2. $$
3. $$
4. $$

Протокол Нидхема—Шрёдера

Протокол Нидхема—Шрёдера (англ. Roger Needham, Michael Shroeder, 1979 год) похож на модифицированный протокол Wide-Mouth Frog, но отличается тем, что доверенный центр (Трент) во время работы основной части протокола не общается со вторым абонентом. Первый абонент получает от доверенного центра специальный пакет, который он без всякой модификации отправляет второму абоненту.

1. $$
2. $$
3. $$
4. $$
5. $$

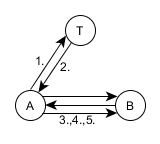
Схема взаимодействия абонентов и довереного центра в протоколе Нидхема—Шрёдера


Протокол обеспечивает и двустороннюю аутентификацию сторон, и, казалось бы, защиту от атак с повторной передачей (англ. replay attack). Последнее делается с помощью введения уже известных по модифицированному протоколу Wide-Mouth From случайных меток $$ и $$. Действительно, без знания ключа злоумышленник не сможет выдать себя за Алису перед Бобом (так как не сможет расшифровать пакет с зашифрованной меткой $$). Однако, как мы договорились ранее во введении к этой главе, сам сессионный ключ не может считаться надёжным длительное время. Если злоумышленник сумеет в какой-то момент времени получить ранее использованный сессионный ключ $$, он сможет убедить Боба, что он является Алисой, и что это новый сессионный ключ. Для этого ему понадобится переданный ранее по открытому каналу пакет из пункта 3 протокола.

1. $$
2. $$
3. $$
4. $$
5. $$
   
   … по прошествии некоторого времени...
6. $$
7. $$
8. $$

Относительно мелкий недостаток протокола состоит ещё и в том, что во втором пакете доверенный центр в зашифрованном виде передаёт то, что в третьем шаге пересылается по открытому каналу ($$).

Если в протокол добавить метки времени, тем самым ограничив время возможного использования сессионного ключа, а также исправить мелкий недостаток с двойным шифрованием, можно получить протокол, который лежит в основе распространённого средства аутентификации «Kerberos» для локальных сетей.

Протокол «Kerberos»

В данном разделе будет описан протокол аутентификации сторон с единственным доверенным центром. Сетевой протокол «Kerberos» использует эти идеи при объединении нескольких доверенных центров в единую сеть для обеспечения надёжности и отказоустойчивости. Подробнее о сетевом протоколе «Kerberos» смотрите в разделе 12.1. «Система Kerberos для локальной сети».

Как и в протоколе Нидхема—Шрёдера, инициирующий абонент (Алиса) общается только с выделенным доверенным центром, получая от него два пакета с зашифрованным сессионным ключом — один для себя, а второй — для вызываемого абонента (Боба). Однако в отличие от Нидхема—Шрёдера в рассматриваемом протоколе зашифрованные пакеты содержат также метку времени $$ и срок действия сессионного ключа $$ (от англ. lifetime — срок жизни). Что позволяет, во-первых, защититься от рассмотренной в предыдущем разделе атаки повтором. А, во-вторых, позволяет доверенному центру в некотором смысле управлять абонентами, заставляя их получать новые сессионные ключи по истечению заранее заданного времени $$.

1. $$
2. $$
3. $$
4. $$

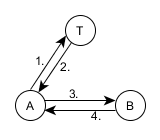
Схема взаимодействия абонентов и довереного центра в протоколе «Kerberos»


Обратите внимание, что третий шаг, за счёт использования метки времени от доверенного центра $$ вместо случайной метки от Боба $$ позволяет сократить протокол на один шаг по сравнению с протоколом Нидхема—Шрёдера. Также наличие метки времени делает ненужным и предварительную генерацию случайной метки Алисой и её передачу на первом шаге.

Интересно отметить, что пакеты $$ и $$ одинаковы по своему формату. В некотором смысле их можно назвать сертификатами сессионного ключа для Алисы и Боба. Причём все подобные пары пакетов можно сгенерировать заранее (например, в начале дня), выложить на общедоступный ресурс, предоставить в свободное использование и выключить доверенный центр (он своё дело уже сделал — сгенерировав эти пакеты). И до момента времени $$ этими «сертификатами» можно пользоваться. Но только если вы являетесь одной из допустимых пар абонентов. Конечно, эта идея непрактична — ведь количество таких пар растёт как квадрат от числа абонентов. Однако интересен тот факт, что подобные пакеты можно сгенерировать заранее. Эта идея нам пригодится при рассмотрении инфраструктуры открытых ключей (public key infrastructure, PKI)).

(далее идёт рассмотрение протоколов с использованием асимметричного шифрования)

Послесловие для тех, кто читал Шнайера и Википедию. Данный раздел основан в основном на третьей главе книги «Прикладная криптография» (издание 2002 года), информация из которой была оформлена в виде лекции, которая была прочитана студентам, которые оформили по итогам презентации (и книги, и других источников) статьи в русском разделе Википедии. Информация из статей (например, об атаках) была далее использована в лекциях и в пособии. Интересно, что Шнайер не стал прослеживать связь между отдельными протоколами, хотя с методической точки зрения всегда интересно проследить эволюцию от простого решения (Wide-Mouth Frog) к сложному (Kerberos). С этой же целью из рассмотрения исключен проколол Yaholom. Он хороший — просто не вписывается в «эволюционную» цепочку. А давать его студентам просто ради «ещё один протокол», как мне кажется, неправильно.