Биткойн и другие криптовалюты захватили внимание огромного количества людей. Почему бы не воспользоваться этим шансом для популяризации математики и, в частности, Mathcad? В этой статье мы рассмотрим несколько простых широко известных моделей на основе дифференциальных уравнений, а именно, семейства логистических моделей (неограниченного роста, с конкуренцией за ресурс, с промыслом и запаздыванием). Впервые системный фактор, ограничивающий рост биологической популяции, предложил бельгийский математик Ферхюльст, поэтому соответствующая модель (она будет рассмотрена второй по счету) по праву носит его имя.

Поскольку все, что происходит в последнее время с с биткойном, похоже на пирамиду, то и модели будут соответствующие, тем более, что математическому аппарату, благодаря МММ, уже в разное время посвящало свои статьи множество коллег, например, М.Баландин и В.Очков. Основное внимание, как и раньше, мы уделим приемам расчетов в Mathcad, в особенности, в его бесплатной версии Mathcad Express, не настаивая на точности прогноза, каким будет курс биткойна в ближайшее время, и когда именно он рухнет.



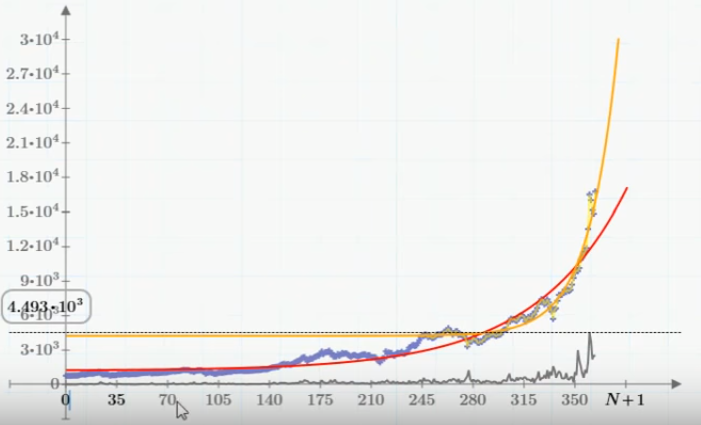
Прежде всего, стоит заметить, что до сих пор, на протяжении последних нескольких месяцев график курса биткойна сильно напоминал экспоненциальный рост (см. график сверху). Т.е. напрашивается использование уравнение типа y'(t)=S*y(t), решением которого является экспоненциальная функция. Чтобы иметь возможность сравнивать в Mathcad экспериментальные данные и результаты моделирования, надо сначала импортировать исходные данные в документ Mathcad. Тому, как это делается (к слову, импорт работает и в бесплатной версии Mathcad Express) я посвятил скринкаст, в котором также показал, как можно интерполировать и экстраполировать данные при помощи экспоненциальной функции. Результат интерполяции-экстраполяции показан на верхнем графике красной (по данным за последний год) и оранжевой (за 4 месяца) кривыми.

В этой статье мы проведем расчет нескольких простых широко известных моделей, на основе обыкновенных дифференциальных уравнений. Они были изначально предложены в качестве моделей роста биологических популяций (см. подробнее, например, тут), а впоследствии стали использоваться для моделирования эпидемий, а также экономических явлений, подобных рассматриваемому. Первая модель y'(t)=S*y(t), где y(t) — мы считаем курсом биткойна в момент времени t. Эта всемирно известная модель была предложена Мальтусом в 1798 г. в его классическом труде «О законе роста народонаселения». Если проводить аналогию с динамикой популяции, а точнее — с распространением эпидемии, то более адекватным было бы считать y(t) общую капитализацию биткойна, т.е. значение текущего курса, умноженное на количество биткойнов. Но поскольку число биткойнов за год изменилось мало (а оно увеличилось благодаря майнингу), то можно для простоты и наглядности y(t) считать текущим курсом.

Обратимся теперь к следующей модели — уравнению Ферхюльста y'=S*y — k*y², в котором последнее слагаемое описывает затухание эпидемии из-за ограниченности ресурса. Соответственно, давайте на этом примере посмотрим как в mathcad prime и mathcad express можно решать обыкновенные дифференциальные уравнения (далее ОДУ). В полнофункциональной версии mathcad prime для этого используется «блок решения», в котором, собственно и записывается начальное условие, само дифференциальное уравнение (оно выделено желтой заливкой), а также встроенная функция mathcad prime, которая его решает.



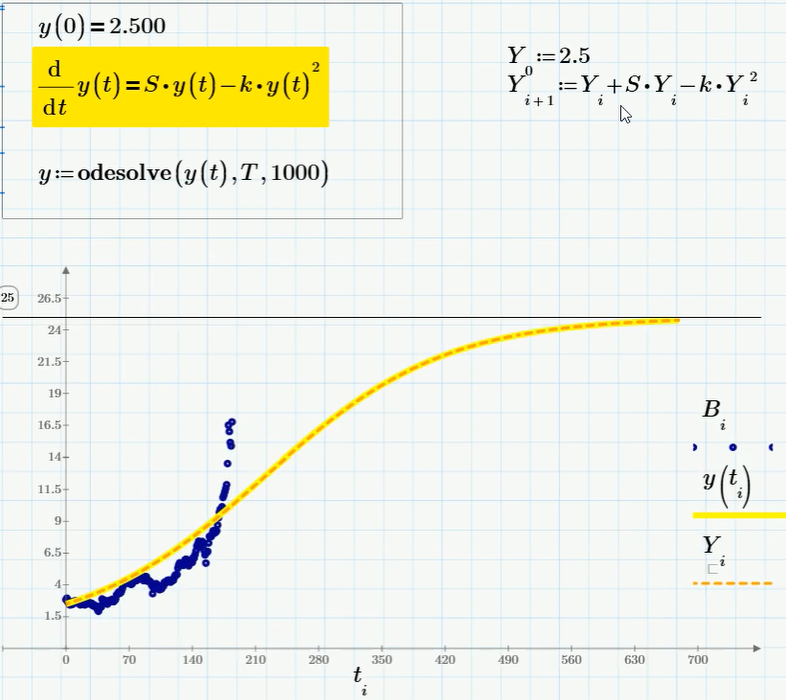
Решение ОДУ при помощи встроенной функции Mathcad Рrime показано в виде желтой кривой. Если вы располагаете только бесплатной версией Mathcad Express, то решение такого несложного ОДУ, как логистическое, легко записать в виде реализации разностной схемы (этому посвящена подробная статья на Хабре). Сама разностная схема содержит всего две строчки расчетов и выписана справа от «блока решения», обведенного в рамку. Решение ОДУ при помощи разностной схемы приведено на том же графике в виде пунктирной кривой, совпадающей с решением y(t). Асимптотическое значение, к которому стремится y(t), равно S/k. Собственно, исходя из этих соображений и подобран коэффициент k. Какой он на самом деле, мы не знаем (биткойн, согласно модели, может расти до 25, а может и до 200, если взять k в 10 раз меньше).

Следующая модель — это небольшое усложнение логистической, а именно, модель динамики популяции, подвергаемой промыслу, т.е. равномерное изъятие из популяции ее определенной доли. Если проводить аналогию с биткойном, то данная модель описывает снижение объема биткойнов за счет их продажи спекулянтами (и/или за счет странной комиссии при обмене на деньги, достигающей, как известно, 10-20%). Также стоит учесть, что промысел (распродажа биткойнов) начинается не с самого начала, а с некоторого момента, например, после достижения равновесного значения S/k. Уравнение и его решение выглядит следующим образом:



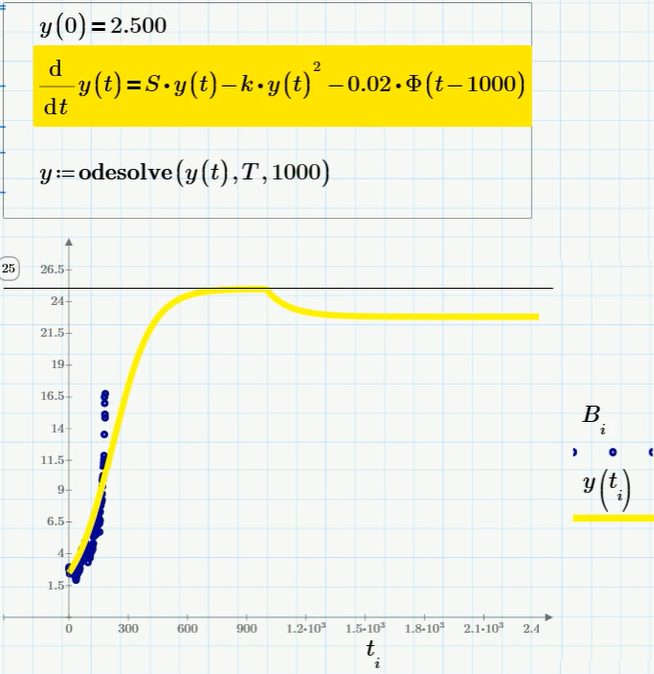
Как видно, промысел обуславливает некоторое снижение равновесного курса (в терминах вычислительной биологии — численности популяции). Но так будет происходить, если только промыслу подвергается не очень большой процент популяции. Если последнее слагаемое в уравнении взять слишком большим (точнее — больше некоторого критического значения), то популяция вместо стремления к асимптотической численности, вымрет (а курс биткойна, если проводить аналогию — обрушится до нуля). Соответствующий график решения (для коэффициента при последнем слагаемом примерно 0.07) показан на рисунке:



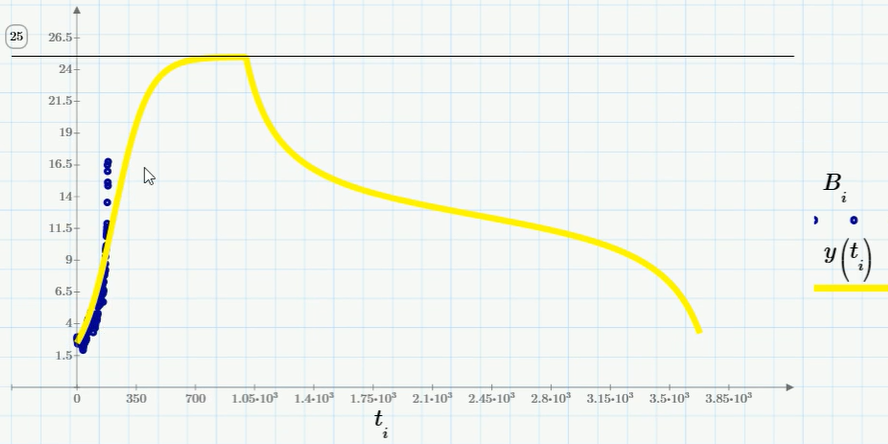
Собственно, вот это уже неплохо описывает финансовую пирамиду: сначала быстрый экспоненциальный рост (модель Мальтуса) — потом насыщение и выход на плато (модель Ферхюльста или логистическая модель с небольшим промыслом) — и в финале неудовлетворенность инвесторов, панические распродажи и падение курса до нуля. Когда это произойдет? Конечно, я не возьмусь предсказывать — возможно, завтра, а возможно, что через год.

Последняя модель, которая характерна для финансового моделирования и которую мне хочется рассмотреть — это «логистическая модель с запаздыванием». Если мы хотим учесть наличие спекулянтов, которые играют на растущем рынке, то наиболее простой способ — это предусмотреть, что они покупают биткойн, держат некоторое время, а затем продают. Для определенности выберем этот период времени равным 120 дням. Тогда соответствующее «логистическое уравнение с запаздыванием» будет слегка отличаться от уравнения Ферхюльста y'=S*y — k*y², а именно включать в качестве последнего слагаемого не квадрат y(t), а произведение двух значений y(t), взятых в два момента времени, отстоящие друг от друга на 120 дней. Это тоже широко известное уравнение y'(t)=S*y(t) — k*y(t)*y(t-120), решить которое можно численно при помощи следующего разностного уравнения в Mathcad Express:



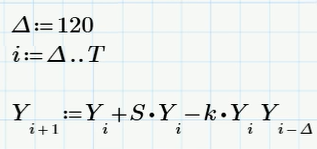
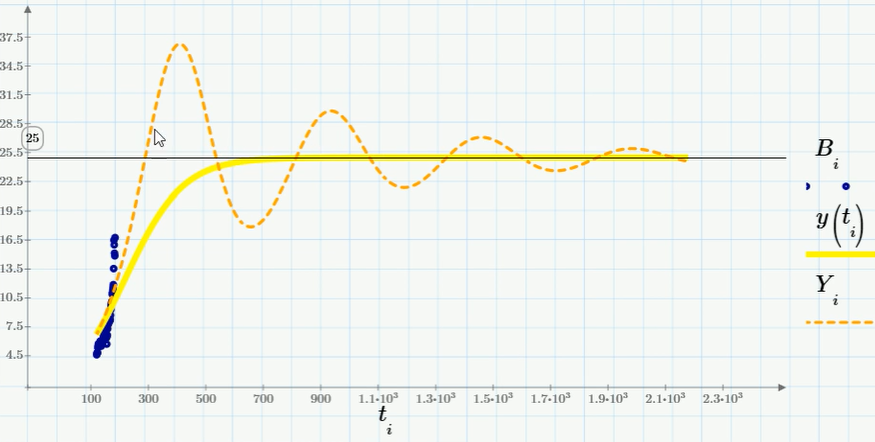
Примечательно, что уравнение с запаздыванием имеет решение в виде затухающих колебаний. И не исключено, что перед обвалом мы увидим (а может быть, даже наблюдаем прямо сейчас?) такую характерную коррекцию курса биткойна. Но все-таки, мне не хочется гадать, поскольку, еще раз, эта статья — удачный повод показать, как в Mathcad решаются дифференциальные уравнения и напомнить читателю о моделях из вычислительной биологии.



В заключение, оставляю ссылку на свой ролик, в котором вся последовательность действий в Mathcad по расчету приведенных моделей описана более подробно.