В статье будет рассказано о том, как ваш покорный слуга значительно повысил эффективность компьютерной модели расчета нестационарных течений газа в крупных системах газоснабжения произвольной конфигурации, благодаря применения библиотеки ManagedCuda и nVidia CUDA 7.0. Однако изложение будет вестись без привязки к конкретной предметной области.
Постановка задачи
Рассматривается классическая задача решения СЛАУ:
Ax=b
Здесь матрица A размером nxn, x — вектор неизвестных размером n, b — вектор известных свободных членов размером n.
Автор статьи занимается разработкой специализированного программно-вычислительного комплекса (ПВК) для моделирования и оптимизации нестационарных течений газа в системах газоснабжения. В решаемых мною задачах A является положительно определенным якобианом с диагональным преобладанием некоторой системы нелинейных уравнений. A получается в результате матричных преобразований матрицы инциденций графа системы газоснабжения и других матриц. В моих практических расчетах A обычно заполнена на 6-10%, остальное нули. Размер же ее зависит от размера конкретной системы газоснабжения и варьируется n от 10 до 1000.
Наш ПВК разрабатывается под .NET 4.0 на C#. Расчетный модуль и вся математика также разрабатывается на C#. Изначально для решения СЛАУ я написал собственную, доморощенную, библиотеку, не использующую технологию разреженных матриц. Для решения СЛАУ применял метод LU декомпозиции. И до поры меня все устраивало, пока я не начал заниматься задачей оптимизацией нестационарных режимов течения газа, где приходится методом динамического программирования осуществлять большое количество переборов значений управляющих параметров и, соответственно, много раз решать СЛАУ. Стандартный профилировщик Visual Studio показал, что в процессе выполнения программы около 40% затрат приходится на решение СЛАУ.
Именно в этот момент я понял, что пора что-то менять.
Математическая библиотека Math.Net Numerics
Проведя анализ имеющихся математических библиотек под .Net я решил остановиться на библиотеке Math.Net Numerics. Подробно ознакомиться с ней вы можете здесь.
Меня заинтересовали ее ключевые возможности:
- Реализована технология разреженные матриц и векторов;
- Имеются встроенные все необходимые вектор-матричные операции;
- Присутствуют встроенные решатели;
- Интуитивно понятный API.
Приведу листинг с примером решения СЛАУ средствами Math.Net Numerics:
SparseMatrix matrix = new SparseMatrix(n);
double[] rightSide = new double[n];
//Заполнение матрицы и вектора правой части
//...
var x = matrix.Solve(DenseVector.Build.DenseOfArray(rightSide)).ToArray();
Как видно, все очень элегантно выглядит, но практически сразу меня настигло разочарование — встроенный решатель Math.Net Numerics работал значительно медленнее моего. Меня это совершенно не устроило, однако претензии к реализованным в библиотеке вектор-матричным операциям не столь существенные. Поэтому полностью отказываться от Math.Net Numerics я не стал, оставив код, где производится работа с векторами и матрицами.
Но тут мне вспомнился весьма удачный опыт коллег по аспирантуре, которые для решения задач подземной гидродинамики использовали графические процессоры. В распоряжении у меня имеется ноутбук с видеокартой nVidia GeeForce GT 540M с 2 GB памяти и поддержкой технологии CUDA. Было принято решение попробовать эту технологию на деле, о чем теперь не жалею.
Библиотека ManagedCuda
О технологии CUDA на этом сайте имеется большое количество материала, поэтому любопытный читатель без особого труда его найдет. Я же остановлюсь на том, как решал поставленную перед собой задачу.
Меня заинтересовала библиотека cuSPARSE. При первом знакомстве с ней я наткнулся на проблемы:
- Непосредственная работа с библиотекой возможна только через C/C++. Конечно, проблема решится, если использовать качественный враппер, который очень не хотелось писать. По результатам поиска был найден CUDA-враппер для .Net под названием Cudafy.
- cuSPARCE позволяет решать СЛАУ с треугольными матрицами, а в моем случае матрицы таковыми не являются. Однако cuSPARSE содержит методы факторизации матриц, приводящие их к треугольной форме (метод LU факторизации, разложение Холецкого). Однако в API Cudafy отсутствовали соответствующие методы, поэтому от Cudafy пришлось отказаться.
После продолжения поиска я открыл для себя библиотеку ManagedCuda, которая является высокоуровневой оберткой над CUDA API. Все её возможности я перечислять не буду — их можно найти на официальном сайте, но остановлюсь на том, как можно, используя Math.Net Numerics и ManagedCuda, элегантно и эффективно решать СЛАУ.
Идея заключается в использовании SparseMatrix из Math.Net Numerics для формирования и хранения разреженной матрицы в формате CSR, который принимают на вход cuSPARSE и ManagedCuda. Далее приводится листинг соответствующей программы:
SparseMatrix matrix = new SparseMatrix(n);
double[] rightSide = new double[n];
//Заполнение матрицы и вектора правой части
//...
var storage = matrix.Storage as SparseCompressedRowMatrixStorage<double>; //Содержит необходимую
//информацию о разреженной матрице в CSR формате
var nonZeroValues = storage.EnumerateNonZero().ToArray(); //Получаем ненулевые элементы матрицы
double[] x = new double[matrix.RowCount]; //Выделяется память под результат расчета
CudaSolveSparse sp = new CudaSolveSparse(); //Создаем решатель из библиотеки ManagedCuda
CudaSparseMatrixDescriptor matrixDescriptor = new CudaSparseMatrixDescriptor(); // Создается дескриптор матрицы
double tolerance = 0.00001; //Точность расчета. Значение взято для иллюстрации
sp.CsrlsvluHost(matrix.RowCount, nonZeroValues.Length, matrixDescriptor, nonZeroValues,
storage.RowPointers, storage.ColumnIndices, rightSide,
tolerance, 0, x); //Решение СЛАУ методом LU факторизации
Вычислительный эксперимент: анализ временных затрат на решению СЛАУ различными технологиями
Дабы не утомлять читателя сухим текстом и листингами программ, рассмотрим результаты расчетов СЛАУ размерностей от 50 до 500 с помощью различных технологий:
- Доморощенный решатель, написанный автором статьи. Назовем его Mani.Net.
- Стандартный решатель библиотеки Math.Net Numerics.
- Метод LU декомпозиции библиотеки ManagedCuda.
Матрица A заполняется на 10% случайным образом.
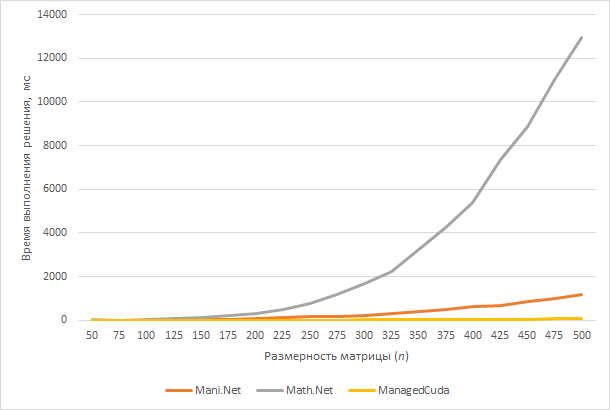
Рисунок наглядно демонстрирует, почему мне пришлось отказаться от Math.Net Numerics для решения СЛАУ.
Отметим, при размерности матрицы равной 500 моему собственному решателю (Mani.Net) потребовалось 1170 мс, Math.Net Numerics — 12968 мс, ManagedCuda — 70 мс.
Заключение
Следует ожидать в комментариях замечания, мол де не на всех машинах есть GPU nVidia с поддержкой CUDA. Действительно, это так. Поэтому наше приложение настроено на две конфигурации компиляции: с собственной библиотекой решения СЛАУ и с ManagedCuda.
Насчет Mani.Net отмечу, что это не реклама моей собственной библиотеки. Найти ее нигде невозможно и никому её я передавать не буду. Нет, я не жадный. Мне стыдно за код.
Спасибо за прочтение статьи! Буду рад узнать о вашем мнении и замечаниях в комментариях.
Комментарии (33)

futureader
23.06.2015 18:49На всякий случай, было бы не плохо проверить, с какой скоростью решают С-шные библиотеки.

manifold Автор
23.06.2015 18:55Согласен. Однако на это время у нас не было. В диссертацию придется обязательно включать сравнение Eigen.

futureader
23.06.2015 19:38Кроме того, насколько я помню, Math.Net не имеет вообще ни какого распараллеливания. Вы пробовали использовать AsParallel? Я понимаю, что умножение матриц вот так просто не распараллелить, но вам скорее всего нужно решать задачу не раз. Если у вас есть доступ к Micrsoft Visual Studio Ultimate, то можно поймать какое же действие наиболее прожорливое.

Anton_Menshov
24.06.2015 01:49Сразу советую сравнивать не с Eigen, а с приличной реализацией BLAS/LAPACK. Или как минимум дать возможность Eigen использовать эту реализацию — точно есть опция через Intel MKL.

rafuck
23.06.2015 22:43+1Или я чего-то не понимаю. Или времена счета какие-то странные. Сейчас просто открыл Matlab и написал в нем следующее:
n = 1000; A = rand(n,n); b = rand(n,1); tic; x = A\b; toc
Выход: Elapsed time is 0.118833 seconds.
Макбук, i7, 2.6 ГГц
Одна десятая секунды. На плотной матрице.
P.S. Прошу прощения за неоформленный листинг, видимо кармы моей недостаточно.
rafuck
23.06.2015 22:54+1500x500 — одна сотая секунды. Еще раз: плотная матрица, счет безо всяких GPU.
Еще пара вопросов: что параллелится? LU-факторизация? Вы используете double. Пробовали float? Если да, насколько быстрей, насколько деградирует точность?
werktone
24.06.2015 00:11Согласен, 500x500 – вообще смешная размерность.
numpy плотную матрицу 500x500 решает за 3 мс на достаточно старом i5. 5000x5000 – за 2 секунды.
In [1]: n = 5000 In [2]: a = np.random.rand(n, n); b = np.random.rand(n, 1) In [3]: t = time.time(); c = np.linalg.solve(a, b); print time.time() - t 2.17847013474
Anton_Menshov
24.06.2015 00:54np.linalg.solve использует процедуру gesv из LAPACK. производительность которой сильно зависит от конкретной матрицы (адаптивном используется одинарная и двойная точность арифметики — как в реализации от Intel). Поэтому замеряя производительность лучше пользоваться другими способами — например прямой вызов (или через интерфейс) пары getrf, getrs из LAPACK, которые вычисляют, соответственно, LU-декомпозицию и решение в той арифметике, которую вы укажете.
Хотя я с вами абсолютно согласен, что ваш пример явно демонстрирует слишком малый размер примера 500 х 500. Нужно подниматься как минимум до 5-10 тысяч.

manifold Автор
25.06.2015 18:29в пример вставил 500x500, т.к. при больших размерностях уже Math.Net неприлично долго считает и графики Mani.Net и ManagedCuda визуально неразличимы.

Anton_Menshov
25.06.2015 23:22Поэтому графики производительности чаще всего строятся в Log-Log масштабе, а данные самого неудачного метода при необходимости экстраполируются.

manifold Автор
25.06.2015 18:27На моем ноутбуке матлабу потребовалось также около одной сотой секунды. В принципе, ваш результат согласуется с ManagedCuda. В расчетах использую double. К сожалению, float пока не пробовал. Это может дать приличный прирост?

Anton_Menshov
23.06.2015 23:19Здесь очень серьезно нужно разбираться в конкретной программе.
Сравнивается прямой метод LU-декомпозиции (сложности порядка O(N^3)) и, если я правильно понимаю, итеративная реализация алгоритма — так как была указана точность решения ( сложность O(N_it * N^2), N_it — число итераций). Количество итераций может меняться в зависимости от обусловленности матрицы. Кроме того, делать стандартную декомпозицию LU для разреженных матриц попросту неэффективно — так как декомпозиция будет плотной матрицей (или как минимум banded). Распараллеливать LU и распараллеливать умножение матрицы на вектор (что используется в итеративных методах) — большая разница. Плюс, к итеративный методам можно и нужно добавлять предобуславливатели (preconditioners), которые уменьшают количество итераций значительно.
Все это сочетает в себе как проблемы решения СЛАУ для конкретной проблемы, так и общую теорию. Хотелось бы больше характеристик того, что именно решалось и как именно решалось. Иначе получается сравнение слонов с носорогами.
manifold Автор
25.06.2015 18:43В своем посте я допустил огрешность, не указав, что в cuSPARSE используется incomplete-LU factorization.
Все-таки я не ставил себе целью провести сравнение различных технологий, а предлагаю решение задачи решения СЛАУ с помощью GPU под .Net. Приведенное сравнение носит иллюстративный характер. Исходил из того, что если бы мне такая статья попалась сразу, то я сэкономил бы много усилий и времени.
Я подготовлю статью о решаемой мной проблеме. Однако беспокоит, что проблема является весьма специфичной — широкому кругу может показаться неинтересной.

splav_asv
23.06.2015 23:23А почему просто не использовать итерационные методы рашения? Тот же GMRES.

Anton_Menshov
24.06.2015 01:00Нужно узнавать у автора, каковы характеристики его матрицы (и, соответственно, самой проблемы):
Обусловленность (Conditioning) Использование предобуславливателя (PreConditioning) Количество «правых» частей уравнения Необходимая точность решения
Делать слепой общий «решатель» СЛАУ итеративным, не зная характеристик матрицы, проблемы и необходимой точности, довольно опрометчиво.
splav_asv
24.06.2015 01:18Это я как раз к тому, рассматривались ли другие методы. И есть ли вообще представление о том, какие методы решения СЛАУ бывают, какие у них особенности.
У автора задача оптимизации вроде бы, обычно там высока точность не требуется.
Если размерность системы велика(500 это маленькая система, прямо скажем), то PC(ilu или еще что, может можно придумать «физический» предобуславливатель) + gmres вполне можно и расмотреть как вариант.
Anton_Menshov
24.06.2015 01:38Да, я что-то не сразу соотнес оптимизацию и требования к точности. Согласен. Хотя для 500 может и никакого PC не нужно. Маааленькое все очень. Просто нужен цивилизованный метод. Вопрос, насколько они собираются расти в размере системы — и тогда асимптотичекая сложность прямого LU в лоб — может быть фатальна.
Я бы, конечно, мог предложить быстрые прямые методы типа иерархических матриц — но здесь это, скорее, overkill.
Вы абсолютно правы, скорее нужно смотреть хорошую реализацию итеративного алгоритма GMRES, BiCGstab (если матрица симметрична или имеет определенные свойства — можно сэкономить на упрощенных реализациях), TFMQR с потенциалом внедрения предобуславливателя. И, разумеется, очень желательно использование библиотеки LAPACK для низкоуровневых операций с векторами и матрицами. Иначе — изобретение велосипеда может получиться.

manifold Автор
25.06.2015 18:48Нет, в статье я указывал, что оптимизационная задача решается методом динамического программирования, но при переборе вариантов приходится решать системы нелинейных уравнений.
О методах решения СЛАУ автор осведомлен в достаточной степени. Свои изыскания я начинал именно с итерационных методов (метод Гаусса-Зейделя). Однако было принято решение использовать прямые методы.
splav_asv
25.06.2015 22:15Ресь про то, что для опимизационных задач обычно не нужно очень тоное решение СЛАУ, обычно 1E-6 вполне хватает. Естественно желательно обазразмеривать коэффициенты СЛУ чтобы они были, по возможности, одного порядка — для улучшения точности.
Тогда поясните пожалуйста, почему именно было решено использовать именно полное LU разложение.
Метод Гаусса-Зейделя не самый распространенный на сегодняшний день, очень редко когда подходит.

rafuck
24.06.2015 10:51Автор указал, насколько я понимаю, что для вычислительных экспериментов использовалась случайно заполненная на 10% матрица. О каком диагональном преобладании, кстати, тут можно говорить, мне непонятно. Может быть, конечно, заполнение не совсем случайное, а, скажем, случайное оно только вне главной диагонали и числами из диапазона [-1, 0], а на диагональ идет сумма по строке. Тем не менее, об этом автор умолчал.

splav_asv
24.06.2015 11:55В данном случае, речь не про эксперимент, а про задачу автора, реальную. Ведь автор для своей реальной задачи данный метод применял изначально.

ALEX_k_s
30.06.2015 14:12Это конечно замечательно, что вы применили ГПУ и воспользовались уже написанной библиотекой, но
1) почему для расчетов используется шарп — ведь по моему ясно, что Си для этих целей куда лучше — и портируемость и поддержка со стороны CUDA/OpenCL/ MPI
2) ваш Mani.net вполне возможно лучше бы работал, если бы был на Си, так как используя CUDA вы выходите на хорошо оптимизированные библиотеки, написанные на Си, так еще и на GPU.
Также может я что то упустил, но не заметил — параллельная ли ваша версия или последовательная? именно то, что сравнивалось на графике. По вашим цифрам получается где то в 16 раз ускорилось.
PS: еще как пожелание — график было бы лучше смотреть, если бы на нем была только ваша версия и GPU, то есть увеличенный масштаб. А то он лишь показывает, что то, с чем вы сравниваетесь — хуже, а конкретно на сколько лучше — не ясно.


halyavin
Почему не хотите использовать С++ библиотеки вроде Eigen (на замену собственной библиотеки на .NET)? Какую библиотеку используете для переупорядочивания вершин?
manifold Автор
1. От нативных библиотек было решено отказаться на этапе концептуального проектирования ПВК. Eigen мы используем в другом проекте, где расчетный модуль разрабатывается на С++.
2. Какие вершины вы имеете ввиду?
halyavin
Переменные и уравнения системы (они у вас скорее всего соответствуют узлам сетки, на которой решаются дифференциальные уравнения в частных производных).
manifold Автор
При решении дифференциальных уравнений в частных производных у нас задача переименования вершин не возникает. Но возникает при моделировании потокораспределения в системах газоснабжения (СГ). На основе графической схемы СГ мы формируем объектный граф. У каждого узла имеется признак, который показывает известны ли в нем параметры газового потока. Далее узлы графа разбиваются на два множества в соответствии с этим признаком обычным linq запросом. И уже для каждого множества узлов строятся два блока матрицы инциденций. На одном из них осуществляется поиск решения. Если будет интересно пользователям, то можно подготовить отдельную публикацию.
halyavin
Переупорядочивание вершин нужно для уменьшения количества ненулевых элементов в LU разложении. Если только у вас сетка не статическая и вы заранее знаете оптимальный порядок, оно нужно всегда. Ну либо если переупорядочивание приводит к неустойчивости и экспоненциальному увеличению погрешности при увеличении размера матрицы.
Anton_Menshov
Насколько я знаю, это обычно делается внутри LU разложения и называется по-английски pivoting (row и\или column). Например, в BLAS\LAPACK реализации Intel MKL. Не уверен, что есть смысл это делать до передачи матрицы к «решателю». Или вы о чем-то другом?
halyavin
Pivoting делается для уменьшения погрешности решения, а переупорядочивание — для уменьшения времени работы. Вот, к примеру, замеры времени при использовании библиотеки METIS: matrixprogramming.com/2008/05/metis.
Anton_Menshov
Хм. Вот она специфика работы с разреженными матрицами — не так часто с ними встречаюсь, как хотелось бы. (все любят, когда их матрица «имеет хорошо обусловленную талию»). Буду иметь ввиду, спасибо.
manifold Автор
Дифуры решаем на статической сетке, т.к. решаем систему уравнений параболического типа. LU разложение в cuSPARSE является неполным, поэтому и количество ненулевых элементов матриц LU регулируется исходя из параметра tolerance. Так я понимаю. Хотя здесь есть над чем задуматься. Спасибо за замечание, с этим стоит разобраться.