Сейчас я попытаюсь дать совсем простое введение в тензоры. Я не претендую на математическую строгость, поэтому некоторые термины могут употребляться не совсем корректно.
Откуда появился термин тензор
Насколько я помню, термин тензор происходит от латинского tensus или английского слова tension — напряжение. Термин возник в процессе осмысления следующей задачи. Пусть нам дано некоторое твердое тело произвольной формы в трехмерном пространстве. К разным концам тела приложены некоторые силы. Как описать возникающие напряжения в некотором сечении этого тела? Ответ на эту задачу — напряжения описываются тензорным полем. Но для понимания этого ответа давайте рассмотрим более простые задачи.
Тензор нулевого ранга
Пусть нам дан в трехмерном пространстве однородный кубик. Давайте его начнем нагревать с какой-либо стороны. Теперь зафиксируем какой-либо момент времени и попробуем описать значения температуры в каждой точке кубика.
Температура — это скаляр, нам нужно только одно число. Введем произвольную систему координат. В рамках этой системы координат температура будет описываться как скалярная функция от (x, y, z).
А давайте теперь возьмем другую систему координат. Что изменится? А ничего! Температура в каждой точке пространства осталась таким же скаляром и при смене системы координат не поменялась.
Вот уже интересно! Мы получили некоторый математический объект, скаляр, который не изменяется при смене системы координат. Назовем его тензором нулевого ранга. Идем дальше.
(Уточнение из комментариев: координаты точек изменятся, но температура в этих точках от поворота системы координат не изменится. Именно температура и есть тензор ранга (0,0))
Тензор первого ранга
Итак, мы нагрели наш однородный кубик. Под действием температуры молекулы какого-либо вещества в нем начали как-то двигаться. Опять зафиксируем какой-либо момент времени и попробуем описать значения скоростей молекул в каждой точке кубика.
Скорость — это вектор. Введем произвольную систему координат. В рамках этой системы скорости в каждой точке пространства будут описываться как векторные функции от (x, y, z). А давайте теперь возьмем другую систему координат? Что изменится? Давайте рассуждать.
Векторное поле скоростей в кубике не изменилось, оно осталось таким же, мы просто взяли другую линейку (другую систему координат) для измерения скоростей. Но изменились компоненты этого вектора. Зная старую и новую систему координат, закон изменения компонент вектора несложно вывести.
Таким образом, мы получили математический объект, вектор, который опять же не изменяется при смене системы координат, но изменяются его компоненты, причем по заранее определенному закону. Это тензор первого ранга. Теперь начинается самое интересное.
Тензор второго ранга
Мы нагрели наш кубик, молекулы начали двигаться. Но представим теперь, что наш кубик перестал быть однородным. Он теперь пористый, внутри состоит из разных каналов с разной ориентацией. Скорость движения молекулы вдоль канала гораздо больше, чем скорость движения поперек канала. Как нам описать такую неоднородную среду?
Зафиксируем какой-либо момент времени, возьмем одну молекулу со своим вектором скорости. Вопрос, как этот вектор скорости изменится в следующий момент времени? Если молекула попала в канал и вектор ее скорости направлен вдоль канала, то скорость не изменится, если вектор направлен поперек канала, то уменьшится в несколько раз, а если под углом, то вектор скорости вообще изменит свое направление.
Это очень похоже на то, что в каждой точке кубика задано нечто, что умеет поворачивать и масштабировать вектора. Да, да, это матрица! Но не произвольная, а специальная, которая не уничтожает вектора, а преобразовывает.
Хорошо, а что будет с нашей матрицей, если мы возьмем другую систему координат, что изменится? Конфигурация каналов в кубике осталась такой же, и эта матрица должна поворачивать вектора скоростей точно таким же образом. Да, компоненты этой матрицы изменятся, но само ее действие на вектора останется таким же.
Таким образом, мы опять же имеем математический объект, матрицу специального вида, действие которой на вектор не зависит от смены системы координат, а ее компоненты пересчитываются по определенному закону. Назовем его тензором второго ранга.
Так что же такое тензор?
Итак, тензор это математический объект, который как объект не зависит от смены системы координат, но его компоненты при смене системы координат преобразуются по определенному математическому закону. В трехмерном пространстве тензор второго ранга проще всего представить как матрицу, заданную в каждой точке пространства, которая описывает неоднородность этого пространства и действует на входящий вектор, изменяя его направление и масштаб.
Комментарии (26)

kirikch
01.07.2015 15:16+5Можете не воспринимать слишком близко, но на мой взгляд, вся статья сводится к «тензор — это геометрический объект».
Это как-то не серьезно. По двум причинам.
Во-первых, принято статьи для хабра делать более насыщенными информацией. С тем, что публиковалось в самом начале проекта это даже не сравнить.
Во-вторых, весь смысл тензоров в том, как проводятся с ними математические операции. Уже определение таких геометрических объектов стоит начинать с того, как изменяются компоненты тензора при замене базиса. А это изменение определяется компонентами матрицы перехода и её обратной. Затем привести примеры тензоров: векторы, линейные преобразования, линейные функции, билинейные функции (скалярное произведение, как частный случай). И неплохо было бы показать, зачем вообще тензоры нужны — как они помогают упрощать и унифицировать запись сложных математических выражений.
С учетом этого получилась бы нормальная статья.
alec_kalinin Автор
01.07.2015 16:22+6Я абсолютно согласен. Но если вы внимательно прочитали начало моей заметки, то я там объясняю, что хочу дать некоторое введение к очень неплохой статье «Магия тензоров». Там как раз все начинается с математики, и мне показалось, что предварительно дать некоторое интуитивное понимание будет неплохо.

alecv
01.07.2015 16:31-2Картнок не хватает. Или даже анимированных GIF-ов.
В принципе, конечно, понятно, но на пальцах.
merlin-vrn
02.07.2015 13:44+3Ландау словно говорит: не пытайтесь обманывать природу, стараясь представить то, что представить нельзя; это недостойно, а кроме того, вы сами окажетесь обманутыми. Лучше доверьтесь разуму. Он вам поможет, он не откажет. Не надо профанации — обращения к представлениям и чувствам там, где они беспомощны. То, что есть достояние ума, а не воображения, надо постигать лишь умом.
…
Он говорил, что они [статьи Гейзенберга и Шредингера] дали ему не только наслаждение истинной научной красотой, но и острое ощущение силы человеческого гения, величайшим триумфом которого является то, что человек способен понять вещи, которые он уже не в силах вообразить.
Не нужны гифы. Не нужны картинки. Для некоторых тензоров возможно придумать естественное визуальное представление, но не для всех. Тезнор как таковой — абстратный объект, придуманный для того, чтобы обобщить математическое описание совершенно разнообразных вещей. Не надо его воображать и представлять себе.
Mrrl
02.07.2015 14:06А при чём тут гифы? Картинки? Визуальное представление? Зрительный канал, конечно, удобная штука, но это далеко не единственный способ что-то представить. Особенно если не стоит задачи передать это представление другим людям.
У тензора есть какие-то свойства. Его поведение на что-то похоже. Он связан с какими-то другими понятиями. Так что он вписан в ассоциативную сеть представлений, и о нём можно спокойно думать. Как о тензоре. Как объект, он не сложнее, чем, скажем, состояние многопоточной программы во время её выполнения. А ведь мы с ними работаем!

Gunnar
01.07.2015 17:48+1Вот здесь визуально и доходчиво. Но по-английски
www.youtube.com/watch?v=f5liqUk0ZTw

progchip666
01.07.2015 19:42+2А давайте теперь возьмем другую систему координат. Что изменится? А ничего! Температура в каждой точке пространства осталась таким же скаляром и при смене системы координат не поменялась.
То ли я не догоняю, то ли это некоторая некорректность в объяснении. Как же ничего не изменится? Как минимум координаты точек то изменятся из-за того, что изменилась система координат.
Keyten
02.07.2015 07:55+1Хм. Я не придумал достаточно хорошего объяснения (наверное, автор сможет), но отмечу, что на просторах интернета есть другое хорошее объяснение, где скаляры — это количество объектов, а тензоры 1+ ранга — деньги. От того, будем ли мы рассчитываться в долларах, рублях, гривнах, йенах… и так далее — изменится лишь стоимость одного объекта в этой системе координат, однако количество задаётся скаляром, и уж точно неизменно, в чём бы мы не рассчитывались.

progchip666
02.07.2015 09:59Я думаю, это ближе к истине. Не то чтобы я совсем не в курсе что такое тензоры, просто считаю что аналогию то автор неплохую придумал, но вот в объяснении явно существую, скажем корректно, спорные моменты.
Смысл при этом он в конце статьи правильно отразил. Это некоторая структура, позволяющая производить описание сложного объекта исключая влияние системы координат отсчёта. Ну по крайней мере я это так понимаю.

maisvendoo
02.07.2015 11:26+3Как же ничего не изменится? Как минимум координаты точек то изменятся из-за того, что изменилась система координат.
Координаты точек изменятся, но температура в этих точках от поворота системы координат не изменится. Именно температура и есть тензор ранга (0,0)
progchip666
02.07.2015 11:38+1Вот теперь всё очень понятно и корректно получилось! Я бы и в статье внёс это уточнение!

Keyten
02.07.2015 17:15+2На самом деле тензоры — просто очень удобный язык для описания ряда явлений.
Например, в дифференциальной геометрии:
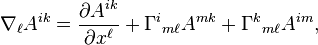
Это ковариантная производная тензора 2 ранга. От обычной производной она отличается тем, что учитывает изменение базиса при переходе в бесконечно близкую точку пространства — в обычных координатах-то он не изменяется, а вот в криволинейных (полярных, сферических и т.п.) — очень даже.
Для обычной (скалярной т.е.) функции ковариантная производная сводится к обычной, а вот для векторных и тензорных функций получается что-то другое…
Гijk — это символы Кристоффеля, не тензор, строго говоря (т.к. изменяется не по тензорному закону при смене базиса), они и описывают изменение базиса при переходе в другую точку криволинейных координат.
Собственно, запоминать этого монстра (производную, не Кристоффеля) совсем необязательно, т.к. благодаря всем тензорным сокращениям и упрощениям он легко выводится для любого ранга.
Слева — тензор 3 ранга (3 индекса). Справа — сумма объектов (необязательно тензоров), тоже 3его.
Но там же пять индексов!
Да.
Пять.
Диагональные одинаковые индексы (m) сворачиваются и исчезают.
Получается три.
Таким образом, для тензора n-го ранга мы просто пишем обычную производную и прибавляем n произведений символа Кристоффеля на тензор, по-разному переставляя индексы, чтобы они сворачивались. Причём для ковариантных индексов (тех, что пишутся снизу) берём со знаком минус.


sheknitrtch
Если вы хотите окунуться поглубже в Тензорный анализ, то могу посоветовать учебник Б. Е. Победря «Лекции по тензорному анализу» 1986г.
Книга требует знаний в линейной алгебре, мат. анализе и аналитической геометрии. Из неё Я узнал про ковариантные и контрвариантные координаты, запись тензоров в Эйнштейновском виде, узнал, что скалярное произведение — это тоже тензор, и лично познакомился с тензором кривизны.
grossws
sheknitrtch
Насколько Я знаю, скалярное произведение в произвольном конечномерном пространстве задаётся матрицей.
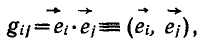
(ei — базисный вектор)
Для декартовой системы координат — это единичная матрица. Для косоугольной — эта матрица будет другой. Но свойства у неё прямо как у тензора. Или Я что-то путаю?
grossws
gij — это метрический тензор, который используется для описания свойств пространства. В простейшем случае он константный. Через него выражается скалярное произведение векторов ai и bj как gij ai bj, которое является скаляром.
Mrrl
Скалярное произведение двух векторов, конечно, скаляр. Но скалярное произведение само по себе, как функция от двух векторов — частный случай билинейной функции, то есть, тензор ранга (0,2).
А в простейшем случае он не просто константный, а единичный (в правильно выбранной системе координат).
grossws
Вопрос в определениях. Если говорить о операции скалярного произведения — то да.
С ортонормированными системами координат тоже всё понятно, много хорошего случается)
Sayonji
Скалярное произведение — всё-таки тензор ранга (1, 1), нет?
Mrrl
Нет, (1,1) — это линейный оператор. (2,0) — бивектор (элемент поверхности), а (0,2) — билинейная функция или квадратичная форма.
Sayonji
Хм, я привык к определению тензора как функционала от нескольких векторов и ковекторов, и по такому определению скалярное произведение как раз оказывается (1, 1), разве нет?
Mrrl
Правильно. Первый индекс — число ковекторов, на которые действует тензор, второе — число векторов. Скалярное произведение действует на два вектора — оно (0,2). Оператор действует на вектор и даёт вектор, или можно сказать, что он действует на вектор и ковектор, и даёт скаляр (по формуле A(v,f)= f(A(v))). Поэтому он (1,1).
Sayonji
Вы правы, прошу прощения. У меня кочему-то лежало в памяти утверждение, что скалярное произведение это функционал над ковектором и вектором, а именно применение одного к другому.