Привет!
Недавно решал задачи с архива Timus Online Judge и наткнулся на раздел под названием задачи динамического программирования. Задачи такого типа вызывают у меня особый интерес, потому что зачастую такой подход обеспечивает быстроту и элегантность решения. Что же такое — динамическое программирование?
Динамическое программирование — это подход к решению задач, при котором происходит разбиение на подзадачи, которые «проще» в сравнении с исходной. Слово «динамический» близко по значению к «индуктивный»: предполагается, что известен ответ для какого-то значения , и хочется найти ответ для . В математике это называется индуктивным переходом, и составляет основную идею динамического программирования.
Наиболее яркой и показательной задачей является задача вычисления -ого числа последовательности Фибоначчи. Известно, что последовательность обладает такими свойствами:
Отсюда сразу вытекает рекуррентная формула:
Если рекурсия ищет число «с конца», то следущий метод последовательно вычисляет все числа, расположенные между и :
Понятно, что при достаточно больших этот алгоритм работает намного быстрее: он не вычисляет промежуточные значения по нескольку раз. Рассмотрим чуть более сложный пример.
Пример 1. Вы шагаете по платной лестнице. Чтобы наступить на -ую ступеньку, необходимо заплатить монет. Вы можете перешагивать на следующую ступень или перепрыгивать через одну. Задача: пройти ступенек и потратить как можно меньше монет.
Понятно, что перешагивая через каждую ступень, мы минимизурем количество «платежей», но можем нарваться на очень дорогую ступень, которую хотелось бы избежать. Создадим массив значений , в котором на -ом месте будет (минимальное) число монет, которые необходимо потратить, чтобы добраться до -ой ступеньки. Сразу ясно, что . А дальше будем брать минимум из двух предыдущих ступенек и добавлять стоимость самой ступеньки:
Немного изменим условия задачи: предположим, что на каких-то ступеньках вы можете получать монеты (это будет означать, что ). Что необходимо изменить в алгоритме, чтобы он давал правильный результат?
Рассмотрим другой пример, в котором используется «двумерная» динамика.
Пример 2. В лабиринте имеется комнат, в каждой из которых находится золото (в клетке лежит золота). Задача — определить, какое максимальное количество золота можно собрать при оптимальном маршруте из точки в точку , если идти можно либо вниз, либо направо.
Итак, мы хотим узнать оптимальный маршрут в клетку . Сюда мы можем попасть из двух клеток — и . С учетом того, что оптимальные маршруты для этих двух клеток известны (они хранятся в какой-то таблице ), то ответ для клетки получается следующим образом:
Эта еще одна классическая задача динамического программирования, модификации которой довольно часто встречаются в задачах спортивного программирования. Более подробно аналогичная задача объясняется здесь.
Математическая формулировка задачи такая: требуется найти минимальное количество слагаемых, необходимых для разложения заданного числа на полные квадраты.
Как и раньше, предположим, что нам известны ответы для всех чисел , которые хранятся в каком-нибудь массиве , и нам бы хотелось найти .
Возьмем это число и проанализируем, какие могут быть ситуации:
Вообще, вариант прибавления единицы к предыдущему кажется не таким уж плохим.
Поступим следующим образом: будем искать разложение такое, что Так как — полный квадрат, то , и то есть мы нашли разбиение, которое просто-напросто лучше, чем , и ответ в этом случае будет
Рассмотрим следующую задачу. Цель — построить лестницу из кубиков по правилам:
На этот раз будем строить двумерную динамику. Создадим табицу , в которой на позиции будет лежать количество лестниц, состоящих из кубиков, высота которых не превосходит . Если получится, то ответом к нашей задаче будет сумма
Итак, будем решать задачу по нахождению количества лестниц, составленных из кубиков, которые имеют высоту . На картинке показаны лестницы, которые попадут в :
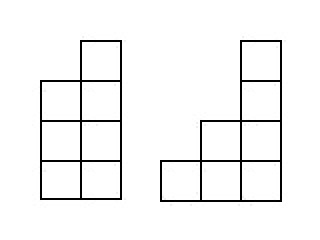
Поскольку нам известны все лестницы, которые состоят из меньшего количества кубиков, то «отщепим» от лестницы правый столбик. В результате получится лестница c кубиками. Пример для :
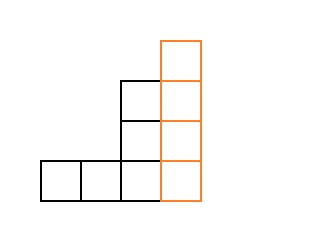
Но для таких лестниц результат уже известен, поэтому переберем все такие лестницы циклом по и сложим все результаты. Таким образом,
Теперь будем перебирать высоты лестниц: Окончательно, изменяя от до , получим ответ.
Важно: в процессе построения нашей матрицы необходимо учитывать , так как в противном случае будут «теряться» некоторые виды лестниц (при «отщеплении»), но разумеется, что такая лестница не удовлетворяет условиям задачи, поэтому в ответе будет число .
Следующая задача решается с использованием одномерного массива.
Итак, что мы имеем. Первый энт знает 2 слова. Каждый энт обучает всем словам, которые знает сам, двух энтов: молодого и старого. В свою очередь, молодого обучили еще стольким же словам, сколько он уже знает, а старого обучили только одному слову. Необходимо узнать, сколько энтов знает в точности слов (необходимо вывести число этих энтов по модулю ).
Решение довольно простое. Создадим массив , в котором на -ом месте будем хранить количество энтов (по модулю ), которые знают слов. Все начинается с первого энта, который знает два слова, поэтому . А дальше все просто:
Осталось разобраться с вычислением по модулю. Для того, чтобы не хранить огромные числа, будем сразу запоминать все значения по модулю.
Используемые ресурсы:
Недавно решал задачи с архива Timus Online Judge и наткнулся на раздел под названием задачи динамического программирования. Задачи такого типа вызывают у меня особый интерес, потому что зачастую такой подход обеспечивает быстроту и элегантность решения. Что же такое — динамическое программирование?
Динамическое программирование — это подход к решению задач, при котором происходит разбиение на подзадачи, которые «проще» в сравнении с исходной. Слово «динамический» близко по значению к «индуктивный»: предполагается, что известен ответ для какого-то значения , и хочется найти ответ для . В математике это называется индуктивным переходом, и составляет основную идею динамического программирования.
Простые примеры
Наиболее яркой и показательной задачей является задача вычисления -ого числа последовательности Фибоначчи. Известно, что последовательность обладает такими свойствами:
Отсюда сразу вытекает рекуррентная формула:
int Fibonacci(int n) {
if(n == 1 || n == 2) return 1;
return Fibonacci(n-1) + Fibonacci(n-2);
}Если рекурсия ищет число «с конца», то следущий метод последовательно вычисляет все числа, расположенные между и :
int dpFibonacci(int n) {
int prev1 = 1;
int prev2 = 1;
int curr = 0;
for(int j = 2; j < n; j++) {
curr = prev1 + prev2;
prev1 = prev2;
prev2 = curr;
}
return curr;
}Понятно, что при достаточно больших этот алгоритм работает намного быстрее: он не вычисляет промежуточные значения по нескольку раз. Рассмотрим чуть более сложный пример.
Пример 1. Вы шагаете по платной лестнице. Чтобы наступить на -ую ступеньку, необходимо заплатить монет. Вы можете перешагивать на следующую ступень или перепрыгивать через одну. Задача: пройти ступенек и потратить как можно меньше монет.
Понятно, что перешагивая через каждую ступень, мы минимизурем количество «платежей», но можем нарваться на очень дорогую ступень, которую хотелось бы избежать. Создадим массив значений , в котором на -ом месте будет (минимальное) число монет, которые необходимо потратить, чтобы добраться до -ой ступеньки. Сразу ясно, что . А дальше будем брать минимум из двух предыдущих ступенек и добавлять стоимость самой ступеньки:
Немного изменим условия задачи: предположим, что на каких-то ступеньках вы можете получать монеты (это будет означать, что ). Что необходимо изменить в алгоритме, чтобы он давал правильный результат?
Решение
Нужно изменить только «начало» нашей динамики. Если первая лестница не приносит нам монет, то желательно перепрыгнуть через нее, однако, если , то лучше наступить и собрать свои монетки. Итак, .
Рассмотрим другой пример, в котором используется «двумерная» динамика.
Пример 2. В лабиринте имеется комнат, в каждой из которых находится золото (в клетке лежит золота). Задача — определить, какое максимальное количество золота можно собрать при оптимальном маршруте из точки в точку , если идти можно либо вниз, либо направо.
Итак, мы хотим узнать оптимальный маршрут в клетку . Сюда мы можем попасть из двух клеток — и . С учетом того, что оптимальные маршруты для этих двух клеток известны (они хранятся в какой-то таблице ), то ответ для клетки получается следующим образом:
Эта еще одна классическая задача динамического программирования, модификации которой довольно часто встречаются в задачах спортивного программирования. Более подробно аналогичная задача объясняется здесь.
Более сложные задачи
При желании динамический подход можно прикрутить куда вздумается. Рассмотрим задачу с архива Timus Online Judge.Математическая формулировка задачи такая: требуется найти минимальное количество слагаемых, необходимых для разложения заданного числа на полные квадраты.
Как и раньше, предположим, что нам известны ответы для всех чисел , которые хранятся в каком-нибудь массиве , и нам бы хотелось найти .
Возьмем это число и проанализируем, какие могут быть ситуации:
- является полным квадратом. В этом случае .
- Возможно, предыдущее число было полным квадратом. Тогда .
Вообще, вариант прибавления единицы к предыдущему кажется не таким уж плохим.
Поступим следующим образом: будем искать разложение такое, что Так как — полный квадрат, то , и то есть мы нашли разбиение, которое просто-напросто лучше, чем , и ответ в этом случае будет
Пример кода на Java, реализующий данный алгоритм:
for(int k = 1; k <= n; k++) {
int best = d[k - 1] + 1; // принимаем этот вариант за наилучший
int q = 1;
while(k - q*q >= 0) { // k = q*q + s
if(k - q*q == 0) { // k - полный квадрат
best = 1;
break;
} else if(d[k - q*q] < best) best = d[k - q*q] + 1;
q++;
}
d[k] = best;
}
Рассмотрим следующую задачу. Цель — построить лестницу из кубиков по правилам:
- лестница имеет минимум две ступени;
- лестница не может иметь две одинаковые ступени;
- ступени лестницы идут в порядке возрастания (то есть следующая больше, чем предыдущая).
На этот раз будем строить двумерную динамику. Создадим табицу , в которой на позиции будет лежать количество лестниц, состоящих из кубиков, высота которых не превосходит . Если получится, то ответом к нашей задаче будет сумма
Итак, будем решать задачу по нахождению количества лестниц, составленных из кубиков, которые имеют высоту . На картинке показаны лестницы, которые попадут в :

Поскольку нам известны все лестницы, которые состоят из меньшего количества кубиков, то «отщепим» от лестницы правый столбик. В результате получится лестница c кубиками. Пример для :
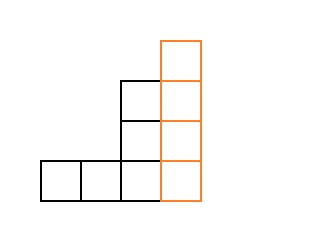
Но для таких лестниц результат уже известен, поэтому переберем все такие лестницы циклом по и сложим все результаты. Таким образом,
Теперь будем перебирать высоты лестниц: Окончательно, изменяя от до , получим ответ.
Важно: в процессе построения нашей матрицы необходимо учитывать , так как в противном случае будут «теряться» некоторые виды лестниц (при «отщеплении»), но разумеется, что такая лестница не удовлетворяет условиям задачи, поэтому в ответе будет число .
Пример кода на Java, реализующий данный алгоритм:
dp = new long[n + 1][n+1];
d[1][1] = 1;
d[2][1] = 0;
d[2][2] = 1;
for(int i = 3; i < n + 1; i++) {
for(int j = 2; j <i; j++) {
long cnt = 0;
for(int k = 1; k < j; k++) {
cnt += d[i - j][k];
}
d[i][j] = cnt;
}
d[i][i] = 1; // добавляем фиктивную лестницу
}
long answer = 0L;
for(int i = 0; i <= n; i++) {
answer += d[n][i];
}
answer--; // вспоминаем про фиктивную лестницу
Следующая задача решается с использованием одномерного массива.
Итак, что мы имеем. Первый энт знает 2 слова. Каждый энт обучает всем словам, которые знает сам, двух энтов: молодого и старого. В свою очередь, молодого обучили еще стольким же словам, сколько он уже знает, а старого обучили только одному слову. Необходимо узнать, сколько энтов знает в точности слов (необходимо вывести число этих энтов по модулю ).
Решение довольно простое. Создадим массив , в котором на -ом месте будем хранить количество энтов (по модулю ), которые знают слов. Все начинается с первого энта, который знает два слова, поэтому . А дальше все просто:
- Все энты, которые знают нечетное количество слов, являются старыми и могли научиться только от предыдущих. Поэтому для нечетных
- Что касается энтов, которые знают четное количество слов — так это все те, кто получил столько же слов от эльфов (молодые) те, кто научился от предыдущих (старые); то есть для четного имеем .
Осталось разобраться с вычислением по модулю. Для того, чтобы не хранить огромные числа, будем сразу запоминать все значения по модулю.
Пример кода на Java, реализующий данный алгоритм:
int[] d = new int[K + 1];
if(K >= 2) d[2] = 1;
if(P != 1) {
for(int i = 3; i <= K; i++) {
if(i % 2 != 0) {
d[i] = d[i - 1];
}
else {
d[i] = ((d[i/2] % P) + d[i - 1] % P) % P;
}
}
} else d[K] = 0;
Используемые ресурсы:
- Timus Online Judge;
- Немного о динамическом программировании;
- Свойства сравнения по модулю.


Izaron
По 1-й задаче — N-ое число Фибоначчи (с условиями — например не само число, которое ни в какие ворота не влезет, а его остаток от деления на MOD=10^9+7) можно еще нескучно находить за O(log(N)) времени, то есть почти бесплатно, даже если N = 10^9 или 10^18 =)
Матрица преобразования размером 2x2 с одним нулем и тремя единицами меняет (a, b) на (b, a + b), то есть на следующую пару Фибоначчи.
Чтобы X раз применить эту матрицу к (a, b) = (0, 1), можно не перемножать по очереди, а сразу найти X^(N-2) бинарным возведением в степень, и применить! После каждого умножения надо только ко всем элементам применить %= MOD.