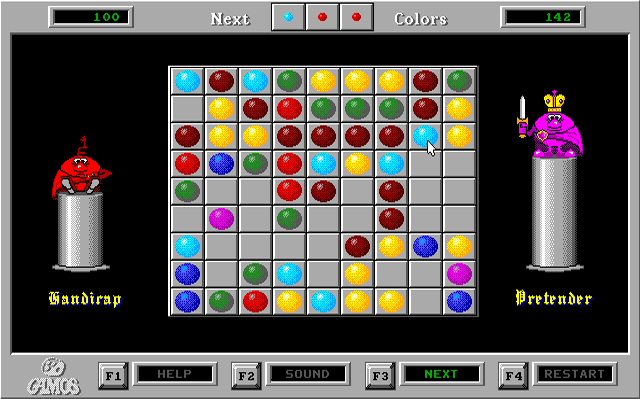
Каждый, кто играл в эту игру, знает: если сейчас попытаться вытащить голубой шарик, на который показывает курсор, чтобы поставить вместо него бордовый, то один из приходящих новых трёх шариков скорее всего «заткнёт» это место. Если попытаться ещё раз вытащить — заткнёт снова. На протяжении всех долгих лет существования этого эффекта между моими коллегами периодически возникали споры, случайно ли это получилось, или нарочно сделана такая «подлянка», чтобы было труднее играть.
По условиям игры считается, что шарики должны выпадать в случайные поля. Но по какой-то причине, если в заваленной части доски имеется свободное поле, оно заполняется в первую очередь.
В этой статье вы сможете вернуться на 20 лет назад и увидеть, как примерно проходил тогда процесс реверс-инжиниринга. Мы рассмотрим 16-битный ассемблерный код, который выбирает место для шариков. Здесь не будет современных 32- и 64-битных инструкций, обрастающих специальными наборами команд, не будет вызовов всяких там dll, потоков и прочих ухищрений. Только простой код. Мне кажется, его поймут даже те, кто ни разу не видел ассемблера. Желающие смогут исправить алгоритм, чтобы он работал «честно».
Начнём с теории. Самый простой напрашивающийся алгоритм такой: выбрать случайное место на доске, а если оно занято, повторить. И так пока не попадём на свободное место. 20 лет назад я думал, что именно такой алгоритм выбрал автор игры и именно поэтому игра такая «нечестная». Я рассуждал так: какова вероятность, что в такой ситуации следующий шарик выпадет в единственное свободное поле в верхней части доски?

Вероятность попадания в верхнюю и в нижнюю половины одинакова, но нижняя почти свободна, а в верхней — всего одно свободное поле. Поэтому если случайное число будет выпадать в нижнюю часть доски, алгоритм сразу завершится, а если в верхнюю — он будет повторяться до тех пор, пока не попадёт в то самое единственное свободное поле. Вот поэтому и получается, что такие свободные поля сразу «затыкаются», и вроде бы всё сходится с реальным поведением игры.
Но человек, знакомый с теорией вероятности, сразу скажет, что это неправильно. Это как вероятность встретить на улице динозавра. Или встретишь, или нет. Вероятность попадания шарика в любую клетку одинакова, независимо от того, сколько и какие клетки заняты. Если за последние 10 ходов ни разу не выпал красный шарик, то я понимаю, что на 11-й ход, скорее всего, он всё-таки выпадет, хотя на самом деле вероятность его выпадения сейчас точно такая же, как 10 ходов назад. Если тут есть еще кто-нибудь, кто не видел "бога тетриса", обязательно посмотрите.
Неужели дело всего лишь в невероятном стечении обстоятельств или в погрешностях генератора псевдослучайных чисел? Есть одно предположение, но не будем забегать вперёд. Пора наконец посмотреть, как всё происходит изнутри.
Возьмем например, английскую floppy-версию игры, хотя вы можете взять любую другую. Для запуска понадобится эмулятор, например dosbox. Для изучения и исправления кода используем Hiew. Его старую DOS-версию автор предлагает скачать на своём сайте бесплатно.
С чего же начать? Как найти то место в программе, где выбирается случайное число? Доска у нас 9х9 клеток. Попробуем поискать 16-битные числа 9 или 81. Девяток находится много, а вот 81 — всего одно. (81 = 51h)

Вот как раз и 9-ки рядом с ним, видимо мы напали на след. Попробуем наобум поменять 51 на 30 и посмотрим, что получится. Запускаем игру, а она сразу закидывает всё поле шариками и зависает. Вот это неожиданно. Неужели это 81 не имеет отношения к размеру поля? Посмотрим, что это за ячейка [343E], куда его записали.

Ну вот же, чуть ниже по коду значение этой ячейки сравнивают с «4C». Хммм. 76? Это еще что такое? Не помню, на какое время этот вопрос поставил меня в тупик, но неожиданно (как и всё в этом процессе) до меня дошло: это число свободных клеток. В самом начале игры появляется 5 шариков. Сначала поле пустое, свободных клеток 81. Потом выкидывают шарики, пока это число не станет 76. Значит это и есть участок кода, где выполняется начальная инициализация доски. Одна из подпрограмм между этими операциями как раз должна выбирать позицию для шарика. Переход по «не равно», помеченный как (8) у нас образует маленький цикл, в котором всего 2 вызова. Посмотрим первый из них.

После стандартных операций со стеком, как видим, берётся число 50h (80), и передаётся как аргумент для вызова какой-то процедуры. Результат она, очевидно, возвращает в регистре AX, который сохраняем в переменной [bp][-2]. Потом берём это число, делим его на 9 (div cx), увеличиваем на 1 (inc ax), меняем местами частное и остаток, и частное сохраняем в ячейке [39E4]. Потом делаем всё то же самое, только сохраняем уже остаток этого же деления в ячейке [39E6].
Ну да, похоже это оно. Подпрограмма — это наверняка случайное число. На выходе мы имеем случайный номер поля. Потом делим его на 9, получаем две координаты, X и Y. На нормальном языке это могло бы выглядеть так:
cell = random(80);
x = cell / 9 + 1;
y = cell % 9 + 1;
Идём дальше:

Берём ранее вычисленные X и Y. Одно из них сдвигаем влево (shl) на 1 бит (умножаем на 2), запоминаем в CX. Другое умножаем на 12 (18), складываем с CX и используем как индекс массива по адресу [3490]. Что это может быть? Ну конечно, содержимое игрового поля, как 2-мерный массив из 16-битных чисел. Поэтому X умножается на 2, а Y на 18. То есть имеем уже:
cell = random(80); // случ.число от 0 до 79
x = cell / 9 + 1;
y = cell % 9 + 1;
if (field[x,y]!=0) ...
И следующий, последний участок, который нам понадобится:

Содержимое клетки сравниваем с нулём. Если это так (видимо клетка свободна?), переходим вперёд на 1E5A. Если нет — увеличиваем номер клетки (который у нас имеет сплошную нумерацию от 0 до 80). Сравниваем его с 51 (81), если меньше — опять же переходим на 1E5A. Если больше — записываем туда ноль, то есть переходим к началу доски. На этом месте все условные ветки у нас сходятся, и что же мы делаем? Повторяется точь-в-точь код с предыдущей картинки для выборки содержимого игрового поля и ещё раз сравнивается с нулём. Если не равно, то переходим назад, на адрес 1E15, а это как раз не самое начало, где выбирается случайное число, а место, где мы из него вычисляем отдельные координаты:
cell = random(80); // случ.число от 0 до 79
next:x = cell / 9 + 1;
y = cell % 9 + 1;
if (field[x,y]!=0)
{
cell++;
if(cell==81) cell=0;
}
if (field[x,y]!=0) goto next;
Вот такой получается алгоритм. Выбираем случайную клетку, а потом, если она занята, просто сдвигаемся по полю слева направо и сверху вниз и по кругу, пока не найдём пустую клетку. Вот и найдена причина «нечестности». Конечно же, при таком алгоритме, вероятность выбора клеток будет очень разная, и зависеть от расположения уже имеющихся на доске шариков.
Проверим, что эта часть кода действительно работает в игре так, как мы предполагаем. Поменяем в начале 50 на 28. Теперь по идее новые шарики должны выпадать только в верхнюю половину доски. Запускаем, и ничего не меняется. Шарики появляются по всей доске.
Оказалось, в программе две почти одинаковых подпрограммы, одна из которых выкидывает 5 шариков случайного цвета в начале игры, а другая — по 3 шарика в ходе игры, но цвета их уже известны (потому что их надо показывать заранее). Copy/paste rules! Ну хорошо, меняем эту вторую подпрограмму, и убеждаемся, что она работает.
Теперь, чтобы алгоритм «честно» ставил шарики на случайные поля, достаточно изменить самый последний переход чуть выше, чтобы он шёл на повторный выбор случайного числа.
2. Переходим в режим дизассемблера (Enter, Enter)
3. Ищем начало процедуры (F7, набираем байты B8 50 00)
4. Смещаемся вниз до нужного перехода (на 1D51)
5. Изменяем адрес перехода (F3, F2, меняем 1CF4 на 1CE8)
6. Выходим из редактирования и сохраняем изменения (Esc, F9)
7. Выходим из hiew
Проверить результат можно даже визуально в игре. Если просто переставлять все шарики в верхнюю часть доски, то постепенно станет заметно, как новые шарики заполняют в первую очередь свободные поля сверху вниз. Особенно это заметно, когда почти вся доска заполнена. После данной модификации такой эффект пропадает, и шарики начинают появляться действительно в случайных местах.
Осталось добавить, что на самом деле должно быть cell = random(81), а не 80. Из-за этой ошибки шарики никогда не выпадают в самую правую нижнюю клетку. Разве что если все клетки левее неё заняты, тогда он попадёт туда за счёт этого «неправильного» алгоритма.
Ах да, и ещё одно. Правильно было бы конечно выбрать случайное число от 1 до числа свободных клеток, и ставить шарик сразу на нужное место, точно зная, что оно свободно, а не повторять цикл, пока он сам не попадёт куда надо. Ведь если останется всего одна последняя клетка, кто знает, сколько раз придётся повторяться? Сколько времени понадобится 16-битному процессору, чтобы выполнить столько циклов? А по теории вероятности, может случиться так, что он вообще никогда туда не попадёт. Но мы ведь знаем, что все эти теории — ерунда, и рано или поздно, а скорее всего циклов через 80, шарик обязательно попадёт в эту единственную клетку.
Комментарии (33)

boeing777
06.07.2015 23:08+1Помню, еще в школе столкнулся с подобной проблемой, когда пытался написать карточного «Дурака»: ломал голову, как же получить случайную карту именно из оставшейся колоды, а не из всей. Правда, уже тогда решение в лоб, то есть пинать рандом до тех пор, пока не выпадет неиспользованная карта, я считал неприемлемым. В итоге было решено использовать множество (писал на дельфи): после использования карта удалялась из множества, а аргумент функции random был равен числу элементов множества. Если бы писал на Си, использовал бы std::vector. Таким образом, мы получаем равновероятный исход (насколько это позволяет random) всего за один вызов, но приходится тратить время на reallocate массива. Думаю, что разработчики Lines нашли компромисс между ресурсами и случайностью, и не было цели сделать подлянку.
На счет последней ячейки небольшая поправка: Вы указали, что шарик попадет туда, только если все ячейки левее будут заняты. Точнее так: если random вернет число 79 (т.е. предпоследняя ячейка), и она окажется занятой, то как раз будет рассмотрена последняя. В принципе это может произойти хоть в начале партии.
ID_Daemon Автор
06.07.2015 23:18Да, я не очень точно выразился. Имелось в виду, что если все клетки от случайно выбранного места до правого нижнего угла будут заняты.

gaelpa
07.07.2015 16:09Странно, я бы скопировал реальный мир и перетасовал бы множество «колоды» в начале игры.

boeing777
07.07.2015 16:19+1Вы будете смеяться, но у меня была паранойя: я не хотел, чтобы кто-то мог прочитать содержимое массива с помощью средств типа artmoney. Но Ваше предложение, безусловно, оптимальнее по скорости.
bigfatbrowncat
08.07.2015 21:46… а если вместо
std::vectorзадействоватьstd::list, то реаллоцировать массив и не придется…
boeing777
08.07.2015 23:05С одной стороны, да. Но в алгоритме необходим доступ к элементу по номеру (оператор []), что является нетипичной операцией для std::list.
bigfatbrowncat
11.07.2015 14:53Поиск элемента по номеру (вернее, пролистывание k элементов по цепочке) — операция несопоставимо более быстрая, нежели
1. Выделить память под n+1
2. Скопировать k-1 и еще n-k элементов
Учитывая, что удалять элемент придется при каждом доступе, этот вариант наверняка быстрее
khim
11.07.2015 16:29Поиск элемента по номеру (вернее, пролистывание
Это с какого-такого перепугу?kэлементов по цепочке) — операция несопоставимо более быстрая
Вспоминаем числа, которые должен знать каждый и замечаем, что чтение из памяти занимает100 ns(грубо), а чтение мегабайта —250,000 ns(тоже грубо), то есть фактически вам всё равно — читать из памяти один байт или байт 300-400. Сколько там у нас данных хранится для одной карты? Один байт? Да пусть даже и десять, всё равноstd::listпроиграет.
1. Выделить память под n+1
Это зачем такой ужас-то?
2. Скопировать k-1 и еще n-k элементов
eraseвstd::listпамять не реаллоцирует и копирует только «хвостовые элементы». В среднем — тоже половину, только для реализации на базеstd::listа «плохие» варианты — когда карта ближе к концу, а для для реализации на базеstd::vectorа — когда ближе к началу.
Учитывая, что удалять элемент придется при каждом доступе, этот вариант наверняка быстрее.
s/быстрее/медленнее/
При удалении карты из массива память не высвобождается, нужно всего-навсего сдвинуть данные о не более, чем о 51й карте. По сравнению с этим высвобождение памяти, которое неизбежно последует за удалением элемента изstd::listа — это просто «умри всё живое»: там с неизбежностью придётся оперировать гигантскими структурами, что будет весьма медленно. Если же у нас странная колода с миллионом карт, то там, конечно, время аллокации/деаллокации станет незаметным, но проблемы со скоростью доступа к памяти никуда не денутся.
Вообще есть хорошее правило: видишь в кодеstd::list— требуй бенчмарков. В 90% случаев это обозначает, что человек не понимает что делает и на самом деле тут нужен либоstd::vector, либоstd::unordered_set, либо, редко,std::set. Задачи, для которыхstd::listоптимален встречаются примерно также часто как солнечные затмения. Они легко придумываются, но редко встречаются на практике.bigfatbrowncat
13.07.2015 11:34чтение из памяти занимает 100 ns (грубо), а чтение мегабайта — 250,000 ns (тоже грубо), то есть фактически вам всё равно — читать из памяти один байт или байт 300-400
Раз уж вы начинаете разговор про оптимизацию, то учтите, пожалуйста, что так как изначальный список будет выделяться, скорее всего, за один прием, а размер кеша процессора намного длиннее, то скорее всего весь список целиком провалится в кеш. Хотя я, конечно, в этом не силен.
Это зачем такой ужас-то? erase в std::list
Не в list, а в vector, который предлагал предыдущий оратор. Я как раз и утверждаю, что удалить элемент из середины вектора много дольше, чем искать по листу.
При удалении карты из массива память не высвобождается, нужно всего-навсего сдвинуть данные о не более, чем о 51й карте. По сравнению с этим высвобождение памяти, которое неизбежно последует за удалением элемента из std::listа — это просто «умри всё живое»
Тут, пожалуй, соглашусь… хотя подзреваю, что освобождение 20 байтов из страницы, принадлежащей приложению, — это операция чуть более сложная, чемnop. Скорее всего она сведется к выкидыванию указателя из таблицы аллокации — и всё. Хотя опять же, утверждать ничего не буду — в подобных случаях предпочитаю обычно не теоретизировать, а измерять. А в конкретном случае вообще спорить не о чем — потери в любом случае ерундовые. Зря я вообще эту дискуссию начал…
khim
13.07.2015 16:18Раз уж вы начинаете разговор про оптимизацию, то учтите, пожалуйста, что так как изначальный список будет выделяться, скорее всего, за один прием, а размер кеша процессора намного длиннее, то скорее всего весь список целиком провалится в кеш.
Только в том случае если ваша программа ничем, кроме тасования карт не занимается. Да и в этом случае вариант с вектором будет быстрее, просто выигрыш будет не ~10-15 раз, а где-то 1.5-2 раза. Не любят современные системы рандомного доступа от слова «совсем». Только кеш первого уровня их нормально обслуживает, но там мизер — от 16KiB до 64KiB даже на самых новейших процессорах. Оттуда и код и данные «вылетают» очень быстро.
Не в list, а в vector, который предлагал предыдущий оратор. Я как раз и утверждаю, что удалить элемент из середины вектора много дольше, чем искать по листу.
Это я опечатался. Конечно речь идёт оeraseвstd::vectorе. Это он аллокациями не занимается и перемещает только «хвост» массива, как я описал.eraseвstd::listе ничего никуда не двигает, понятно, но платит за это слишком большую цену.
Тут, пожалуй, соглашусь… хотя подзреваю, что освобождение 20 байтов из страницы, принадлежащей приложению, — это операция чуть более сложная, чем
И да и нет. Вам в любом случае нужно простись где-то по 3-5 указателям в среднем (иногда больше в зависимости от того как аллокатор сделан), что, понятно, копейки, но обращение к массиву объёмом в ~50 байт — всё равно стоит много дешевле.nop.
Просто этот пример очень близок оказался к оптимизации, которую мы в нашем JIT'е недавно делали. Там тоже шла обработка списков инструкций и изначально использовалсяstd::listсо всеми его накладными расходами. Потому что иногда инструкции нужно вставлять в середину списка и удалять оттуда. Но оказалось, чтоstd::vectorпотому что просто меньше памяти расходует, а то, что вставление/удаление элементов стоит «дорого» оказалось неважно. И это — типичный случай. Проблема в том, что в случае, когда работа устроена как «пройтись поstd::listы, подёргать пару элементов», тоstd::vector, как правило, выигрывает: пройтись по нему быстрее, а что «подёргать пару элеменов» — это уже не так важно! Выигрышstd::listдаёт тогда, когда вы имеете огромный список с которым работаете локально — то есть не просматриваете весь список (или его существенную часть), а обрабатываете как-нибудь хитро близко расположенные элементы. Это, вообще говоря, редко случается.
Причём это одно из вещей, про которые у людей неправильное представление. Совсем неправильное. Дело в том, что «когда компьютеры были большими» обращение в память было не таким дорогим. И списки действительно имели смысл. Они и сейчас имеют смысл где-нибудь в микроконтроллерах, где память встроена в CPU. А вот на PC «disk is the new tape, and RAM is the new disk», так что многие вещи оказываются устроены совсем по другому… Но учат-то в ВУЗах студентов люди, которые хорошо помнять «старые времена» и плохо знают современную архитектуру! Приходится переучивать…

khim
09.07.2015 04:32Вот только не надо нам
std::listа. Не то, что он никогда не может быть нужен, но в 9 случаях из 10 его использование — ошибка проектирования системы.
michael_vostrikov
07.07.2015 08:27+2Ведь если останется всего одна последняя клетка, кто знает, сколько раз придётся повторяться? Сколько времени понадобится 16-битному процессору, чтобы выполнить столько циклов?
Не совсем по теме статьи, но реально встречался с подобной ошибкой в продакшене. В системе использовалась довольно старая и сильно допиленная версия osTicket. Там есть возможность генерировать дополнительный случайный номер для заявки.
Выглядит это так (class.ticket.php):
function genExtRandID() { global $cfg; // We can allow collissions...extId and email must be unique ...so same id with diff emails is ok.. // But for clarity...we are going to make sure it is unique. $id=Misc::randNumber(EXT_TICKET_ID_LEN); if(db_num_rows(db_query('SELECT ticket_id FROM '.TICKET_TABLE.' WHERE ticketID='.db_input($id)))) return Ticket::genExtRandID(); return $id; }
EXT_TICKET_ID_LEN по умолчанию равно 6.
В итоге, когда количество заявок превысило примерно полмиллиона, система начала случайным образом падать при создании заявки. Потому что предел рекурсии 100 вызовов. Долго не могли понять, в чем дело, ошибка-то не воспроизводится.
f0rk
07.07.2015 16:08Много раз подобный код видел, и не могу понять, что мешает людям auto increment поле использовать в качестве extId? Даже если поле сильно секретное, то добавлять к нему случайную строку фиксированного размера, и никаких странных проверок делать не надо. Этот пример еще ничего, иногда бывает такое месиво из каких-то случайных чисел от которых вычисляется md5 что-то добавляется а потом все равно ищется в базе… В основном в php коде, кстати.

SKolotienko
07.07.2015 20:01Хороший пример плохого применения рекурсии вместо циклов.

khim
08.07.2015 15:55У кого? У разработчиков PHP? Даже приличные компиляторы C тут хвостовую рекурсию сотворят, а во многих языках — это основной способ реализации циклов.

rednaxi
09.07.2015 06:14Предел рекурсии 100 вызовов это не ограничение пхп, это расширение suhosin добавляет. Отключается в настройках и спокойно живете дальше.
michael_vostrikov
10.07.2015 07:26Да, перепутал немного, 100 вызовов это было на моей машине, это ограничение XDebug. А на сервере падала по превышению лимита памяти либо по таймауту выполнения.

dtestyk
07.07.2015 15:31Когда решал подобную задачу просто последовательно проходил по всем элементам, пересчитывая вероятность для каждого: первый элемент выбираем с вероятностью m/n, второй — (m-1)/(n-1), если выбрали и m/(n-1), если нет. То есть для получения вероятности выбора текущего элемента делим число оставшихся для выбора элементов на число оставшихся.
m — число элементов, которые нужно выбрать
n — общее число элементов
vlivyur
07.07.2015 17:11+1Я б генерил случайное число до 81. А потом циклически проходил бы столько пустых клеток.

grechnik
07.07.2015 17:26Если так, то первая пустая клетка будет выпадать всегда более вероятно, чем последняя. Например, при постановке второго шарика числа 0 и 80 приведут к первой пустой клетке, что сделает её в два раза более вероятной, чем любую другую (к которой приведёт только одно число).
vlivyur
07.07.2015 17:34Кажется да, чем ближе к началу, тем более вероятно. Тогда продолжаем от последнего шарика, а не с начала.

SKolotienko
07.07.2015 20:03+1Корректнее — генерить случаное число до <количество пустых клеток> и потом проходить столько пустых клеток.


bigfatbrowncat
Вот вы пошутили, а кто-нибудь возьмет да поверит…
sim-dev
Мой сын (школьник, перешел в 10-й класс) учился на курсах «программистов» и в качестве выпускного экзамена их группа делала «сетевой морской бой». Так вот, сын мой решил сделать вариант игры с компьютером (инициативно) и как раз по процитированному алгоритму. В результате когда на игровом поле остается буквально пара свободных клеток (остальные или простреляны, или заняты, или недопустимы по правилам) компьютер тратит иногда до пары минут на «случайный» выбор клетки, куда надо стрелять.
Так что теория теорией, а практика показывает, что «рано или поздно» на самом деле может быть «очень поздно».
Чтобы было понятнее: писал он на C#, между ходами компьютера делал задержки по 500 мс (иначе при удачных ходах играть было неинтересно — за доли секунды убивалось по 2-3 корабля). Вот эти самые 0,5 секунды и давали большую задержку при выборе одной из двух пустых клеток…
frol
Хмм, из вашего последнего предложения следует, что пауза была поставлена сразу после получения случайного числа, что достаточно наивно. Если бы пауза была поставлена уже после проверки на «нестреляность», то не должно было быть всё так печально. Пара минут — 120 секунд с задержками по 0.5 секунды — это всего лишь 240 «холостых выстрелов».
khim
Именно. А 240 пустых выстрелов у нас случаются с вероятностью 8%, что не так и мало. Вот, скажем, 10'000 выстрелов уже могут потребоваться в одном случае из 1043. Конечно при абсолютно случайном ГСЧ, но в любом случае: если бы задержка была вставлена после проверки допустимости, то никто и никогда бы этих задержек не заметил. Даже если бы Lines запускали на старом, древнем, IBM PC с процессором на 4.77MHz.
sim-dev
Наивно? Ну а что вы хотите от первой попытки сделать свою программу? Конечно наивно.
SVlad
То есть, задержка не после завершения выстрела, а после попытки выстрелить, но до проверок?
Тогда 2 минуты — 240 попыток для угадывания 1 из 100.