В этой статье рассматриваются сходства и различия двух подходов к решению алгоритмических задач: динамического программирования (dynamic programing) и принципа «разделяй и властвуй» (divide and conquer). Сравнение будем производить на примере, соответственно, двух алгоритмов: бинарного поиска (как быстро найти число в отсортированном массиве) и расстояния Левенштейна (как преобразовать одну строку в другую с минимальным количеством операций).

Хочу сразу заметить, что данное сравнение и объяснение не претендует на исключительную правильность. И возможно даже некоторые преподаватели в университетах захотели бы меня отчислить :) Эта статья является всего-лишь моей персональной попыткой разложить себе же все по полочками и понять что такое динамическое программирование и каким образом в нем участвует принцип «divide and conquer».

Итак, приступим…

Проблема

Когда я начал изучать алгоритмы мне было сложно понять основную идею динамического программирования (далее DP, от Dynamic Programming) и чем оно отличается от подхода «разделяй и властвуй» (далее DC, от divide-and-conquer). Когда дело доходит до сравнения этих двух парадигм обычно многие успешно используют функцию Фибоначчи для иллюстрации. И это отличная иллюстрация. Но мне кажется, что когда мы используем одну и ту же задачу для иллюстрации DP и DC, то мы теряем одну важную деталь, которая может помочь нам уловить различие между двумя подходами быстрее. И эта деталь состоит в том, что эти две техники наилучшим образом проявляются при решении разного типа задач.

Я все еще в процессе изучения DP и DC и не могу сказать, что я полностью разобрался с этими концепциями. Но я все же надеюсь, что эта статья прольет дополнительный свет и поможет сделать очередной шаг в изучении таких значимых подходов, как dynamic programming and divide-and-conquer.

Сходство DP и DC

То, как я вижу эти две концепции сейчас, могу заключить, что DP является расширенной версией DC.

Я бы не считал их чем-то совершенно различным. Потому что обе эти концепции рекурсивно разбивают проблему на две или более под-проблемы одного и того-де типа до тех пор, пока эти под-проблемы не станут достаточно легкими, чтобы решить их «в лоб», непосредственно. Далее все решения под-проблем объединяются вместе для того, чтобы в итоге дать ответ на оригинальную, изначальную проблему.

Итак, почему же тогда мы все еще имеем два разных подхода (DP и DC) и почему я назвал динамическое программирование расширением. Это потому, что динамическое программирование может быть применено к задачами, которые обладают определенными характеристиками и ограничениями. И только в этом случае DP расширяет DC посредством двух техник: мемоизации (memoization) и табуляции (tabulation).

Давайте немного углубимся в детали…

Ограничения и характеристики необходимые для динамического программирования

Как мы только что с вами выяснили, есть две ключевых характеристики, которыми должна обладать задача/проблема для того, чтобы мы могли попытаться решить ее с помощью динамического программирования:

1. Оптимальная под-структура?—?должно быть возможным составить оптимальное решение задачи из оптимального решения ее под-задач.
2. Пересекающиеся под-проблемы?— проблема должна быть разбиваемой на под-проблемы, которые в свою очередь многократно используются заново. Другими словами, рекурсивный подход к решению проблемы предполагал бы многократное (не однократное) решение одной и той же под-проблемы, вместо того, чтобы производить в каждом рекурсивном цикле все новые и уникальные под-проблемы.

Как только мы сможем найти эти две характеристики в рассматриваемой нами задаче, мы можем сказать, что она может быть решена с использованием динамического программирования.

Динамическое программирование, как расширение принципа «разделяй и властвуй»

DP расширяет DC с помощью двух техник (мемоизация и табулация), целью которых является сохранение решений под-проблем для их дальнейшего многократного использования. Таким образом решения под-проблем кешируются, что приводит к значительному улучшению производительности алгоритма. Например, временная сложность (time complexity) «наивной» рекурсивной имплементации функции Фибоначчи — O(2n). В то время, как решение, основанное на динамическом программировании, выполняется всего-лишь за время О(n).

Мемоизация (заполнения кеша сверху-вниз) является техникой кеширования, которая использует заново ранее вычисленные решения под-задач. Функция Фибоначчи с использованием техники мемоизации выглядела бы так:

memFib(n) {
    if (mem[n] is undefined)
        if (n < 2) result = n
        else result = memFib(n-2) + memFib(n-1)
        mem[n] = result
    return mem[n]
}

Табуляция (заполнение кеша снизу-вверх) является схожей техникой, но которая в первую очередь сфокусирована на заполнении кеша, а не на поиске решения под-проблемы. Вычисление значений, которые необходимо поместить в кеш легче всего в данном случае выполнять итеративно, а не рекурсивно. Функция Фибоначчи с использованием техники табуляции выглядела бы так:

tabFib(n) {
    mem[0] = 0
    mem[1] = 1
    for i = 2...n
        mem[i] = mem[i-2] + mem[i-1]
    return mem[n]
}

Более детально о сравнении мемоизации и табуляции вы можете прочитать здесь.

Основная мысль, которую необходимо уловить в этих примерах, заключается в том, что поскольку у нашей DC проблемы есть пересекающиеся под-проблемы, то мы можем использовать кеширование решений под-проблем с помощью одной из двух техник кеширования: мемоизации и табуляции.

Итак, в чем же в конце концов разница между DP и DC

Мы ознакомились с ограничениями и предпосылками использования динамического программирования, а так же с техниками кеширования используемыми в DP подходе. Давайте попытаемся суммировать и изобразить изложенные выше мысли в следующей иллюстрации:



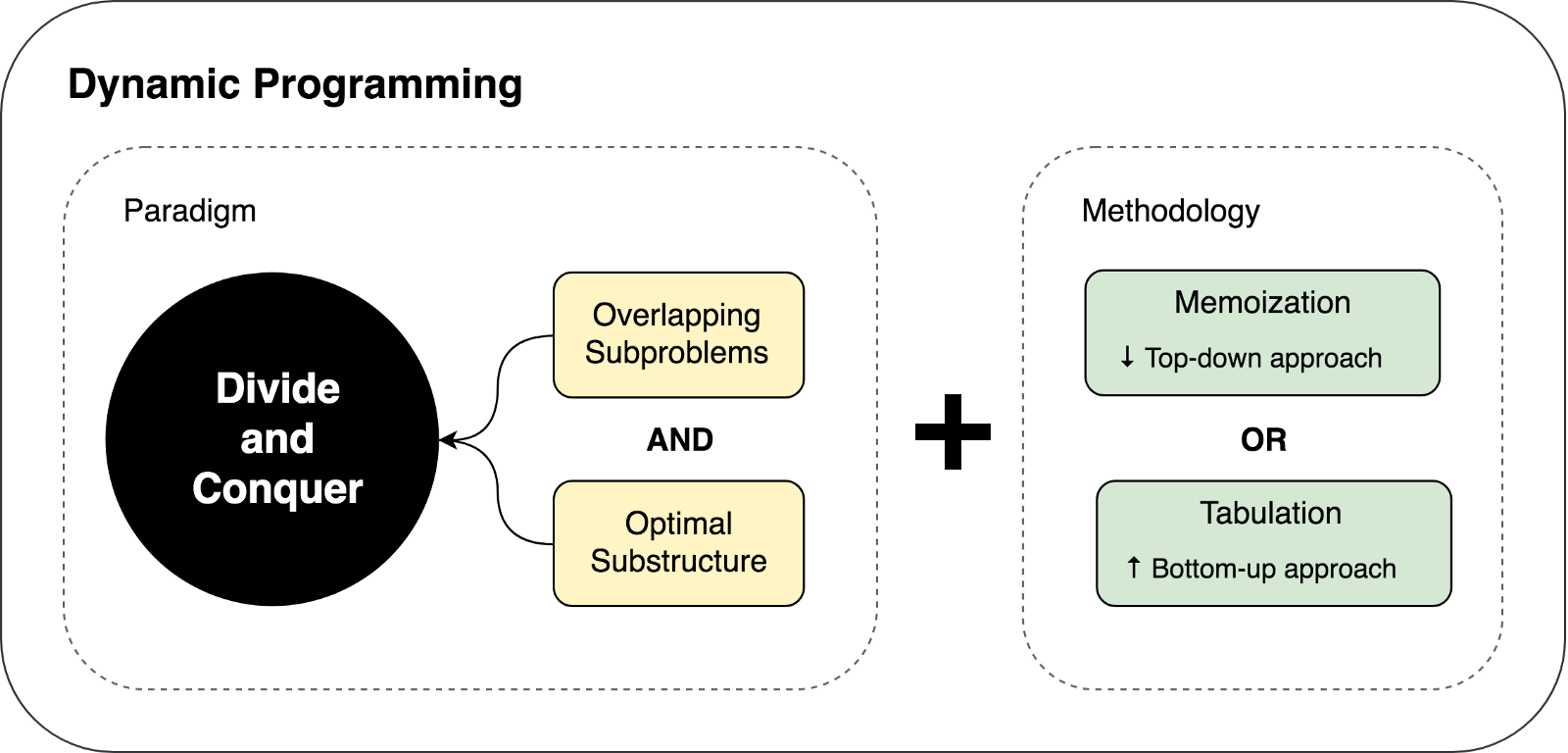
Давайте попытаемся решить пару задач с использованием DP и DC, чтобы продемонстрировать оба этих подхода в действии.

Пример принципа «разделяй и властвуй»: Бинарный поиск

Алгоритм бинарного поиска является поисковым алгоритмом, который находит позицию запрашиваемого элемента в отсортированном массиве. В бинарном поиске мы сравниваем значение искомой переменной со значением элемента в середине массива. Если они не равны, то половина массива, в которой искомый элемент не может находиться исключается из дальнейшего поиска. Поиск продолжается в той половине массива, в которой может находиться искомая переменная до тех пор, пока она не будет найдена. Если же очередная половина массива не содержит элементов, поиск считается законченными и мы делаем вывод, что массив не содержит искомого значения.

Пример

На иллюстрации ниже — пример бинарного поиска числа 4 в массиве.



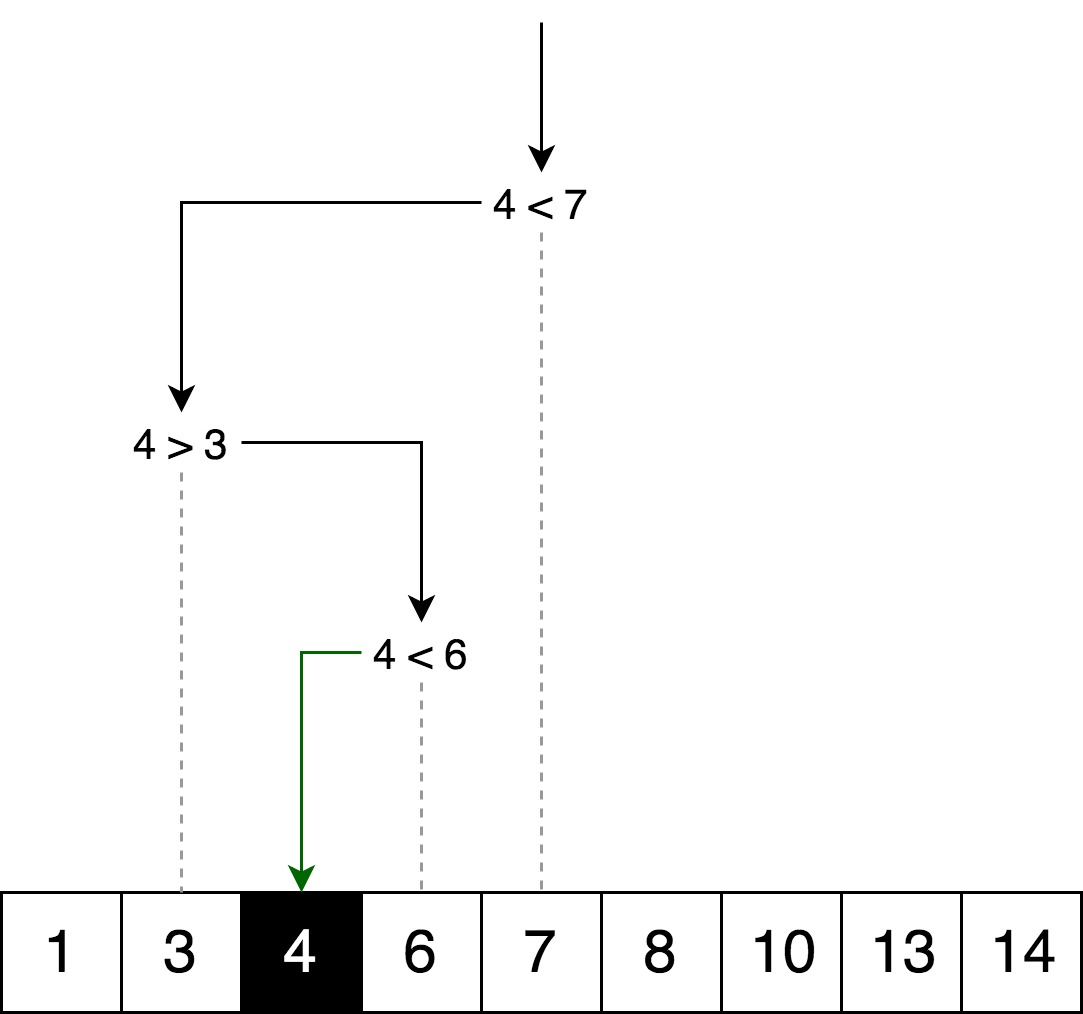
Давайте изобразим ту же логику поиска но в форме «дерева решений» (decision tree).



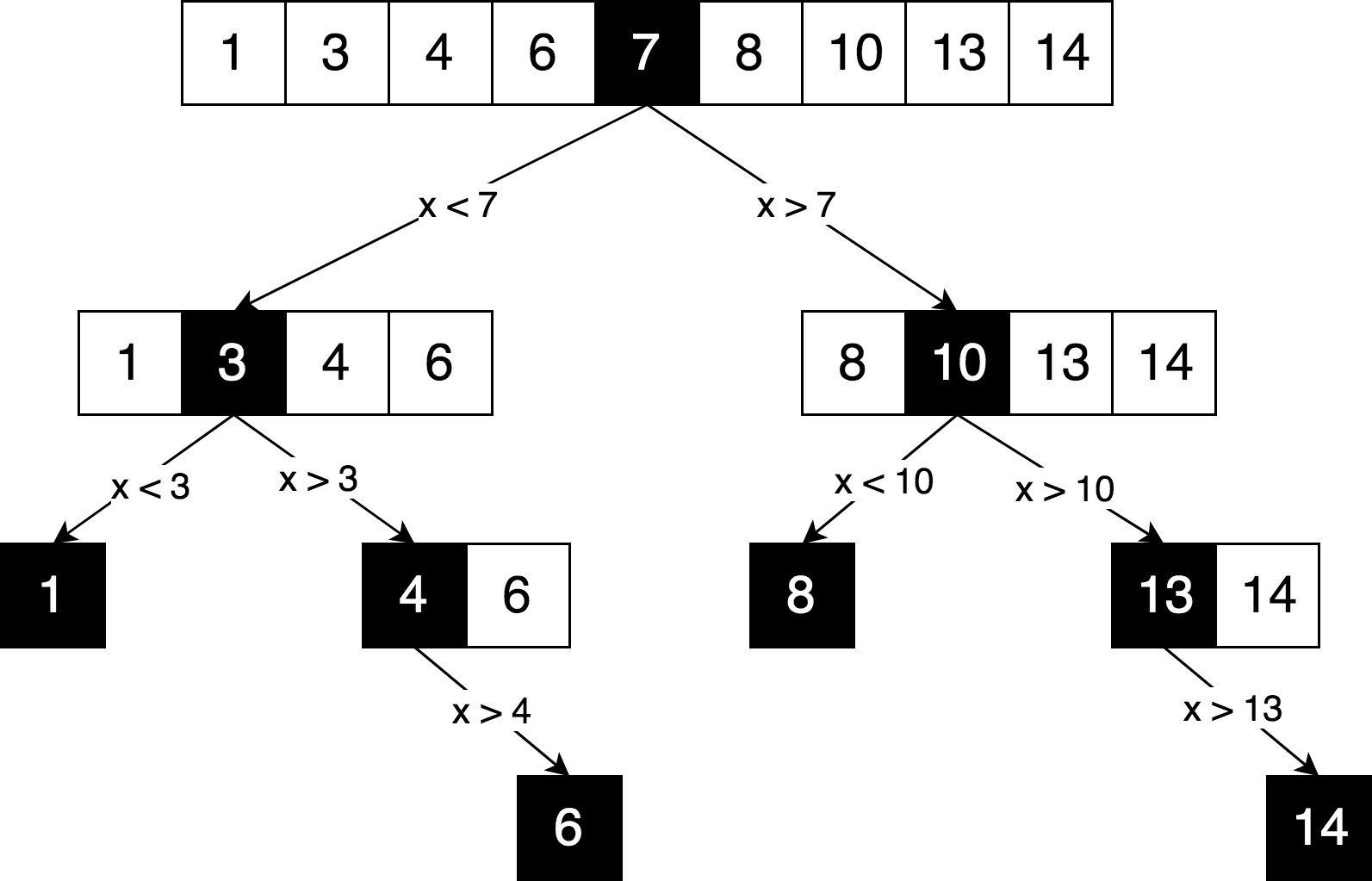
Вы можете увидеть в этой схеме четкий принцип «разделяй и властвуй», используемый для решения этой проблемы. Мы итеративно разбиваем наш оригинальный массив на под-массивы и пытаемся найти искомый элемент уже в них.

Можем ли мы решить эту задачи с использованием динамического программирования? Нет. По той причине, что данная задача не содержит пересекающихся под-проблем. Каждый раз, когда мы разбиваем массив на части, обе части являются полностью независимыми и не пересекающимися. А согласно предпосылкам и ограничениям динамического программирования, которые мы обсуждали выше, под-проблемы должны каким-то образом пересекаться, они должны быть повторяющимися.

Обычно, всякий раз, когда дерево решений выглядит именно как дерево (а не как граф), это скорее всего означает отсутствие пересекающихся под-проблем,

Имплементация алгоритма

Здесь вы можете найти полный исходный код алгоритма бинарного поиска с тестами и объяснениями.

function binarySearch(sortedArray, seekElement) {
  let startIndex = 0;
  let endIndex = sortedArray.length - 1;
  while (startIndex <= endIndex) {
    const middleIndex = startIndex + Math.floor((endIndex - startIndex) / 2);
    // If we've found the element just return its position.
    if (sortedArray[middleIndex] === seekElement)) {
      return middleIndex;
    }
    // Decide which half to choose: left or right one.
    if (sortedArray[middleIndex] < seekElement)) {
      // Go to the right half of the array.
      startIndex = middleIndex + 1;
    } else {
      // Go to the left half of the array.
      endIndex = middleIndex - 1;
    }
  }
  return -1;
}

Пример динамического программирования: Дистанция редактирования

Обычно, когда дело доходит до объяснения динамического программирования, в качестве примера используется функция Фибоначчи. Но в нашем случае, давайте возьмем немного более сложный пример. Чем больше примеров, тем легче разобраться с концепцией.

Дистанция редактирования (или расстояние Левенштейна) между двумя строками это минимальное количество операций вставки одного символа, удаления одного символа и замены одного символа на другой, необходимых для превращения одной строки в другую.

Пример

Например, дистанция редактирования между словами «kitten» and «sitting» равна 3, поскольку необходимо произвести три операции редактирования (две замены и одну вставку), чтобы преобразовать одну строку в другую. И невозможно найти более быстрый вариант преобразования с меньшим количеством операций:

1. kitten > sitten (замена «k» на «s»)
2. sitten > sittin (замена «e» на «i»)
3. sittin > sitting (вставка «g» вконец).

Применение алгоритма

Алгоритм имеет широкую область применения, например, для проверки орфографии, систем корректировки оптического распознавания, неточный поиск строки и пр.

Математическое определение проблемы

Математически расстояние Левенштайна между двумя строками a, b (с длинами |a| и |b| соответственно) определяется функция function lev(|a|, |b|), где: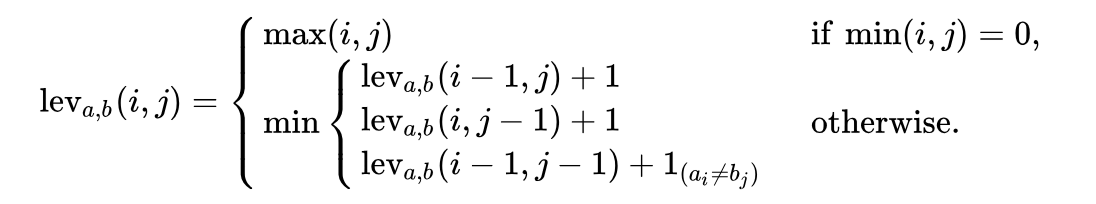



Обратите внимание, первая строка в функции min соответствует операции удаления, вторая строка соответствует операции вставки и третья строка соответствует операции замены (в случае, если буквы не равны).

Объяснение

Давайте попробуем разобраться, о чем нам говорит эта формула. Возьмем простой пример поиска минимальной дистанции редактирования между строками ME и MY. Интуитивно вы уже знаете, что минимальная дистанция редактирования равна одной (1) операции замены (заменить «E» на «Y»). Но давайте формализуем наше решение и превратим его в алгоритмическую форму, для того, чтобы иметь возможность решать более сложные версии этой задачи, такой как трансформация слова Saturday в Sunday.

Для того, чтобы применить формулу к трансформации ME>MY мы сначала должны узнать минимальную дистанцию редактирования между ME>M, M>MY и M>M. Далее мы должны выбрать из трех дистанций минимальную и добавить к ней одну операцию (+1) трансформации E>Y.

Итак, мы уже можем увидеть рекурсивную природу этого решения: минимальная дистанция редактирования ME>MY вычисляется на основании трех предыдущих возможных трансформаций. Таким образом мы уже можем сказать, что это алгоритм «разделяй и властвуй».

Для дальнейшего объяснения алгоритма давайте поместим две наших строки в матрицу:



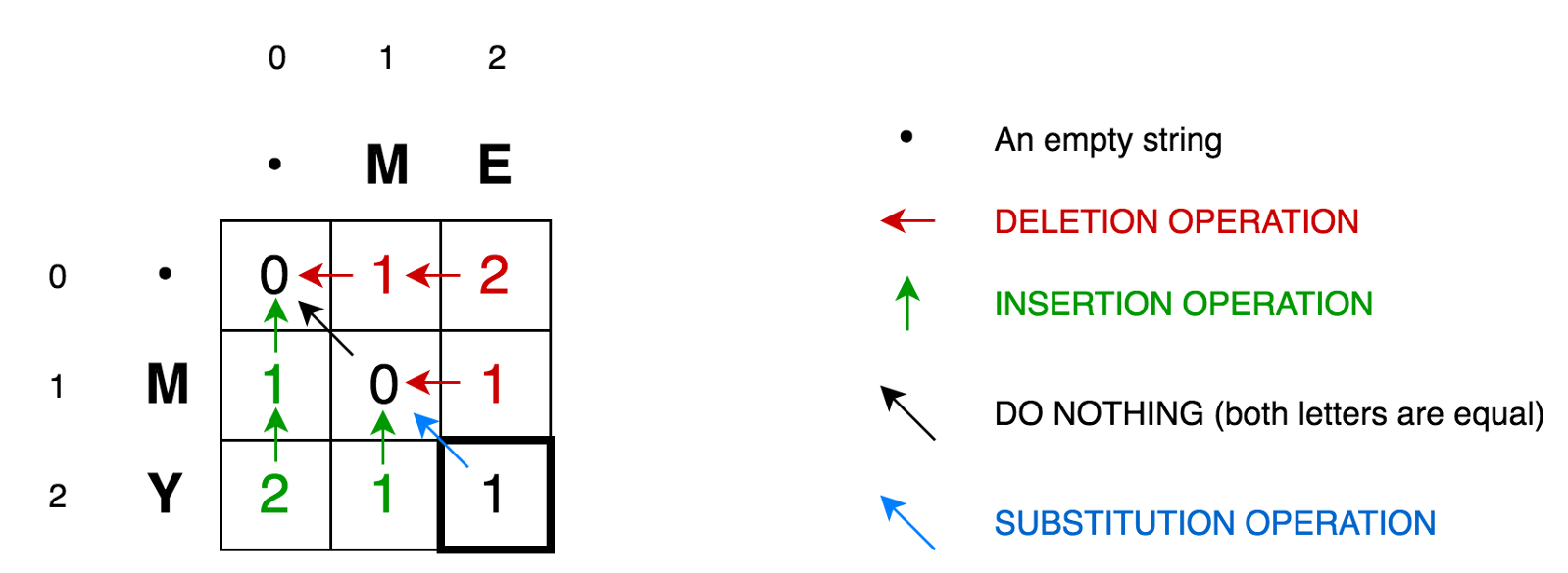
Ячейка (0,1) содержит красное число 1. Это означает, то нам необходимо выполнить 1 операцию для того, чтобы преобразовать M в пустую строку — удалить M. Поэтому мы обозначили это число красным цветом.

Ячейка (0,2) содержит красное число 2. Это означает, что нам надо выполнить 2 операции для того, чтобы трансформировать строку ME в пустую строку — удалить E, удалить M.

Ячейка (1,0) содержит зеленое число 1. Это означает, что нам необходима 1 операция, чтобы трансформировать пустую строку в M — вставить M. Операцию вставки мы отметили зеленым цветом.

Ячейка (2,0) содержит зеленое число 2. Это означает, что нам необходимо выполнить 2 операции для того, чтобы преобразовать пустую строку в строку MY — вставить Y, вставить M.

Ячейка (1,1) содержит число 0. Это означает, что нам не надо делать ни одно операции, для того, чтобы преобразовать строку M в M.

Ячейка (1,2) содержит красное число 1. Это означает, что нам необходимо выполнить 1 операцию, чтобы трансформировать строку ME в М — удалить E.

И так далее…

Это выглядит не сложно для маленьких матриц, таких как наша (всего 3х3). Но как мы можем рассчитать значения всех ячеек для больших матриц (как например для матрицы 9х7 при трансформации Saturday>Sunday)?

Хорошая новость в том, что, согласно формуле, все, что нам необходимо для расчета значения любой ячейки с координатами (i,j) — это всего-лишь значения 3-х соседних ячеек (i-1,j), (i-1,j-1), и (i,j-1). Все, что нам необходимо сделать это найти минимальное значение трех соседних ячеек и добавить к этому значению единицу (+1) в случае, если у нас разные буквы в i-м ряду и j-й колонке.

Итак, повторюсь, вы можете четко увидеть рекурсивную природу данной задачи.



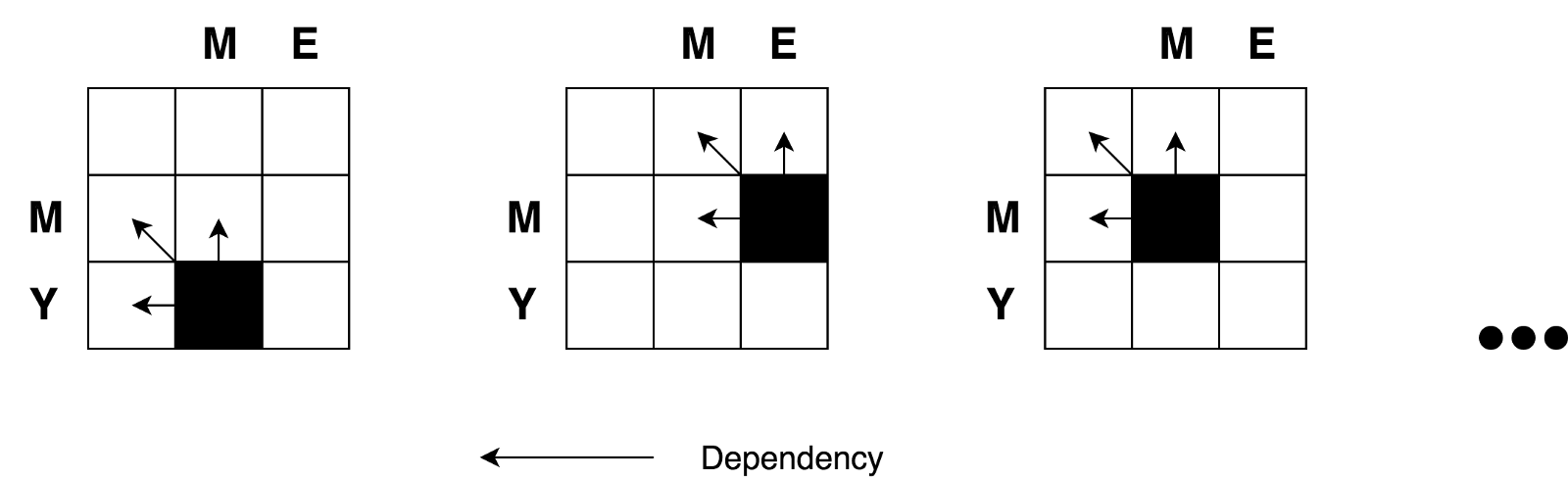
Мы так же увидели, что имеем дело с задачей типа «разделяй и властвуй». Но, можем ли мы применить динамическое программирование для решения этой задачи? Удовлетворяет ли данная задача упомянутым выше условиям "пересекающихся проблем" и "оптимальных под-структур"? Да. Давайте построим дерево принятий решений.



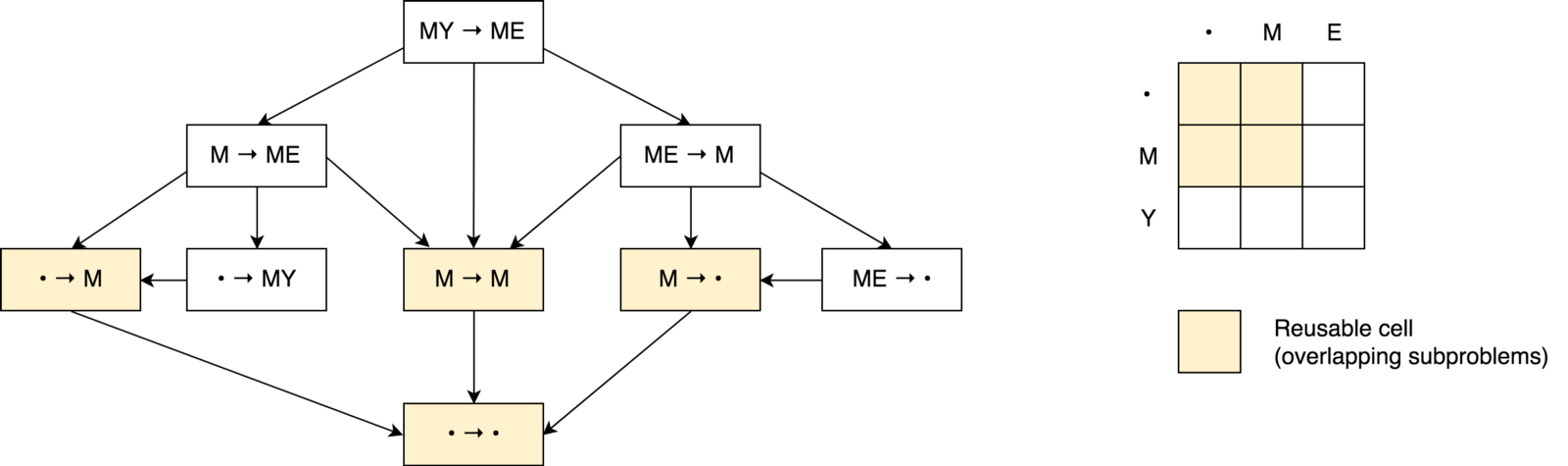
Во-первых вы можете заметить, что наше дерево решений выглядит скорее не как дерево, а как граф решений. Вы так же можете заметить несколько пересекающихся под-задач. Так же видно, что невозможно уменьшить количество операций и сделать его меньшим, чем количество операций с тех трех соседних ячейках (под-проблемах).

Так же вы можете заметить, что значение в каждой ячейке вычисляется на основании предыдущих значений. Таким образом в данном случае применяется техника табуляции (заполнение кеша в направлении снизу-вверх). Вы увидите это в примере кода ниже.

Применяя все эти принципы, мы можем решать более сложные задачи, например задачу трансформации Saturday>Sunday:



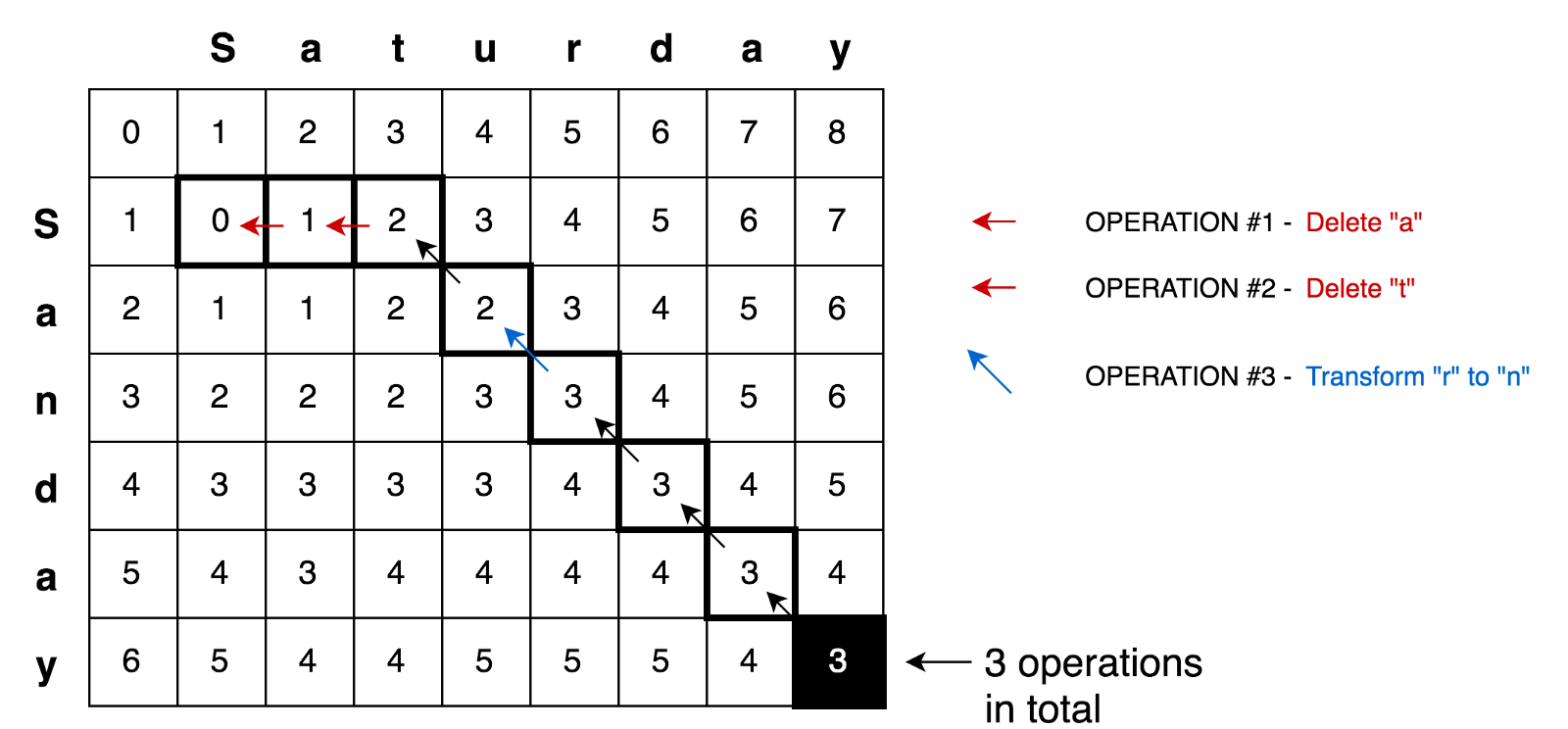
Пример кода

Здесь вы можете найти полное решение поиска минимальной дистанции редактирования с тестами и объяснениями:

function levenshteinDistance(a, b) {
  const distanceMatrix = Array(b.length + 1)
    .fill(null)
    .map(
      () => Array(a.length + 1).fill(null)
    );
  for (let i = 0; i <= a.length; i += 1) {
    distanceMatrix[0][i] = i;
  }
  for (let j = 0; j <= b.length; j += 1) {
    distanceMatrix[j][0] = j;
  }
  for (let j = 1; j <= b.length; j += 1) {
    for (let i = 1; i <= a.length; i += 1) {
      const indicator = a[i - 1] === b[j - 1] ? 0 : 1;
      
      distanceMatrix[j][i] = Math.min(
        distanceMatrix[j][i - 1] + 1, // deletion
        distanceMatrix[j - 1][i] + 1, // insertion
        distanceMatrix[j - 1][i - 1] + indicator, // substitution
      );
    }
  }
  return distanceMatrix[b.length][a.length];
}

Выводы

В этой статье мы сравнили два алгоритмических подхода («динамическое программирование» и «разделяй и властвуй») к решению задач. Мы обнаружили, что динамическое программирование использует принцип «разделяй и властвуй» и можем быть применимо к решению задач в случае, если задача содержит пересекающиеся под-проблемы и оптимальную под-структуру (как в случае с расстоянием Левенштейна). Динамическое программирование далее использует техники мемоизации и табуляции для сохранения под-решений для дальнейшего их повторного использования.

Я надеюсь эта статья скорее прояснила, а не усложнила ситуацию для тех из вас, кто пытался разобраться с такими важными концепциями как динамическое программирование и «разделяй и властвуй» :)

Вы можете найти больше алгоритмических примеров, использующих динамическое программирование, с тестами и объяснениями в репозитории JavaScript Algorithms and Data Structures.

Успешного кодинга!