Одной из важнейших задач в сфере data science является не только построение модели, способной делать качественные предсказания, но и умение интерпретировать такие предсказания.
Если мы не просто знаем, что клиент склонен купить товар, но так же понимаем, что влияет на его покупку, мы сможем в будущем выстраивать стратегию компанию, направленную на повышение эффективности продаж.
Или модель предсказала, что пациент скоро заболеет. Точность таких предсказаний не бывает очень высокой, т.к. много скрытых от модели факторов, но объяснение причин, почему модель сделала такое предсказание, может помочь доктору обратить внимание на новые симптомы. Таким образом, можно расширить границы применения модели, если её точность сама по себе не слишком высока.
В этом посте я хочу рассказать о технике SHAP, которая позволяет заглянуть под капот самых разных моделей.
Если с линейными моделями всё более менее понятно, чем больше абсолютное значение коэффициента при предикторе, тем данный предиктор важнее, то объяснить важность фичей того же градиентного бустинга заметно сложнее.

В стеке sklearn, в пакетах xgboost, lightGBM были встроенные методы оценки важности фичей (feature importance) для «деревянных моделей»:
Основная проблема во всех этих подходах, что непонятно, как именно данная фича влияет на предсказание модели. Например, мы узнали, что уровень дохода важен для оценки платежеспособности клиента банка для выплаты кредита. Но как именно? Насколько сильно более высокий доход смещает предсказания модели?
Мы, конечно, можем сделать несколько предсказаний, меняя уровень дохода. Но что делать с другими фичами? Ведь мы попадаем в ситуацию, что надо получить понимание влияние дохода независимо от других фичей, при их некотором среднем значении.
Есть этакий среднестатистический клиент банка «в вакууме». Как будут меняться предсказания модели в зависимости от изменения дохода?
Тут-то на помощь и приходит библиотека SHAP.
В библиотеке SHAP для оценки важности фичей рассчитываются значения Шэпли (по имени американского математика и названа библиотека).
Для оценки важности фичи происходит оценка предсказаний модели с и без данной фичи.

Значения Шэпли идут из теории игр.
Рассмотрим сценарий: группа людей играет в карты. Как распределить призовой фонд между ними в соответствие с их вкладом?
Делается ряд допущений:
Мы представляем фичи модели в качестве игроков, а призовой фонд — как итоговое предсказание модели.
Формула для расчета значения Шэпли для i-той фичи:
Здесь:
— это предсказание модели с i-той фичей,
— это предсказание модели без i-той фичи,
— количество фичей,
— произвольный набор фичей без i-той фичи
Значение Шэпли для i-той фичи рассчитывается для каждого сэмпла данных (например, для каждого клиента в выборке) на всех возможных комбинациях фичей (включая отсутствие всех фичей), затем полученные значения суммируются по модулю и получается итоговая важность i-той фичи.
Данные вычисления чрезвычайно затратны, поэтому под капотом используются различные алгоритмы оптимизации вычислений, подробнее можно посмотреть по ссылке выше на гитхабе.
Возьмём ванильный пример из документации xgboost.
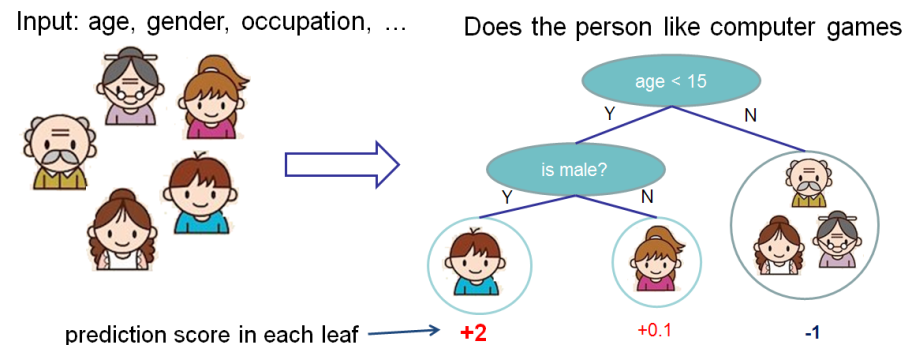
Мы хотим оценить важность фичей для предсказания, нравятся ли человеку компьютерные игры.
В этом примере для простоты у нас есть две фичи: age (возраст) и gender (пол). Gender (пол) принимает значения 0 и 1.
Возьмём Bobby (маленький мальчик в самом левом узле дерева) и посчитаем значение Шэпли для фичи age (возраст).
У нас есть два набора фичей S:
— нет фичей,
— есть только фича пол.
Разные модели по-разному работают с ситуациями, когда для сэмпла данных нет фичей, то есть для всех фичей значения равны NULL.
Будет считать в данному случае, что модель усредняет предсказания по веткам дерева, то есть предсказание без фичей будет .
Если же мы добавим знание возраста, то предсказание модели будет .
В итоге значение Шэпли для случая отсутствия фичей:
Для Bobby для предсказание без фичи возраст, только с фичей пол, равно . Если же мы знаем возраст, то предсказание — это самое левое дерево, то есть 2.
В итоге значение Шэпли для этого случая:
Итогое значение Шэпли для фичи age (возраст):
Библиотека SHAP обладает богатым функционалом визуализации, который помогает легко и просто объяснить модель как для бизнеса, так и для самого аналитика, чтобы оценить адекватность модели.
На одном из проектов я анализировал отток сотрудников из компании. В качестве модели использовался xgboost.
Код в python:
Получившийся график важности фичей:
Как его читать:
Из графика можно сделать интересные выводы и проверить их адекватность:
Можно сразу сформировать портрет уходящего сотрудника: eму не повышали зарплату, он достаточно молод, холост, долгое время на одной позиции, не было повышений грейда, не было высоких годовых оценок, он стал мало общаться с коллегами.
Просто и удобно!
Можно объяснить предсказание для конкретного сотрудника:

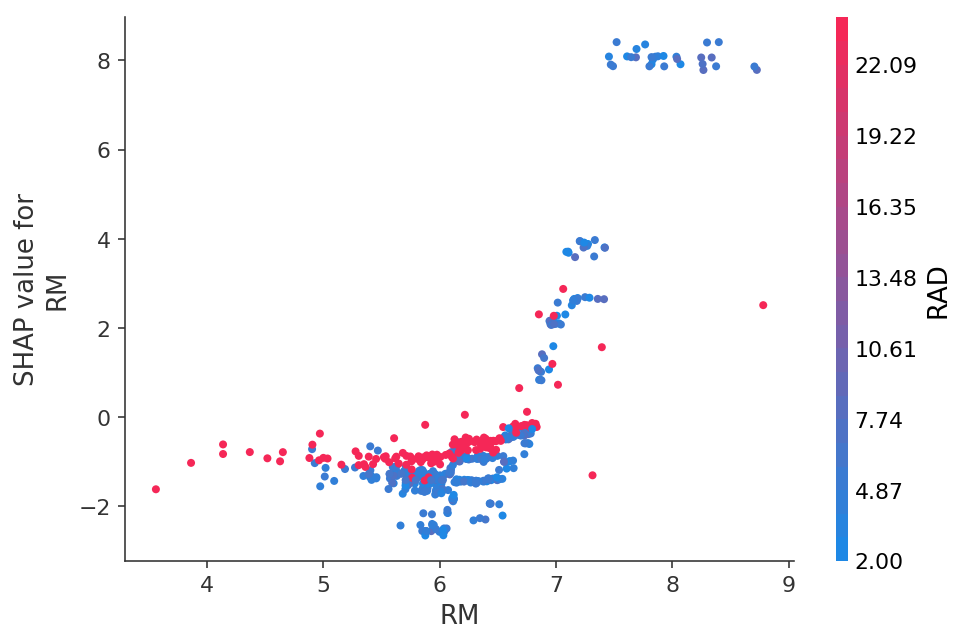
Или посмотреть зависимость предсказаний от конкретной фичи в виде 2D графика:
Можно визуализировать даже предсказания нейронных сетей на картинках:

Я сам узнал о SHAP значениях около полугода назад и это полностью заменило другие методы оценки важности фичей.
Главные преимущества:
Если мы не просто знаем, что клиент склонен купить товар, но так же понимаем, что влияет на его покупку, мы сможем в будущем выстраивать стратегию компанию, направленную на повышение эффективности продаж.
Или модель предсказала, что пациент скоро заболеет. Точность таких предсказаний не бывает очень высокой, т.к. много скрытых от модели факторов, но объяснение причин, почему модель сделала такое предсказание, может помочь доктору обратить внимание на новые симптомы. Таким образом, можно расширить границы применения модели, если её точность сама по себе не слишком высока.
В этом посте я хочу рассказать о технике SHAP, которая позволяет заглянуть под капот самых разных моделей.
Если с линейными моделями всё более менее понятно, чем больше абсолютное значение коэффициента при предикторе, тем данный предиктор важнее, то объяснить важность фичей того же градиентного бустинга заметно сложнее.
Почему возникла необходимости в такой библиотеке

В стеке sklearn, в пакетах xgboost, lightGBM были встроенные методы оценки важности фичей (feature importance) для «деревянных моделей»:
- Gain
Эта мера показывает относительный вклад каждой фичи в модель. для расчета мы идем по каждому дереву, смотрим в каждом узле дерева какая фича приводит к разбиению узла и насколько снижаетcя неопределенность модели согласно метрике (Gini impurity, information gain).
Для каждой фичи суммируется её вклад по всем деревьям.
- Cover
Показывает количество наблюдений для каждой фичи. Например, у вас 4 фичи, 3 дерева. Предположим, фича 1 в узлах дерева содержит 10, 5 и 2 наблюдения в деревьях 1, 2 и 3 соответственно Тогда для данной фичи важность будет равна 17 (10 + 5 + 2).
- Frequency
Показывает, как часто данная фича встречается в узлах дерева, то есть считается суммарное количество разбиений дерева на узлы для каждой фичи в каждом дереве.
Основная проблема во всех этих подходах, что непонятно, как именно данная фича влияет на предсказание модели. Например, мы узнали, что уровень дохода важен для оценки платежеспособности клиента банка для выплаты кредита. Но как именно? Насколько сильно более высокий доход смещает предсказания модели?
Мы, конечно, можем сделать несколько предсказаний, меняя уровень дохода. Но что делать с другими фичами? Ведь мы попадаем в ситуацию, что надо получить понимание влияние дохода независимо от других фичей, при их некотором среднем значении.
Есть этакий среднестатистический клиент банка «в вакууме». Как будут меняться предсказания модели в зависимости от изменения дохода?
Тут-то на помощь и приходит библиотека SHAP.
Рассчитываем важность фичей с помощью SHAP
В библиотеке SHAP для оценки важности фичей рассчитываются значения Шэпли (по имени американского математика и названа библиотека).
Для оценки важности фичи происходит оценка предсказаний модели с и без данной фичи.
Немного предистории

Значения Шэпли идут из теории игр.
Рассмотрим сценарий: группа людей играет в карты. Как распределить призовой фонд между ними в соответствие с их вкладом?
Делается ряд допущений:
- Сумма вознаграждения каждого игрока равна общей сумме призового фонда
- Если два игрока сделали равный вклад в игру, они получают равную награду
- Если игрок не внес никакого вклада, он не получает вознаграждения
- Если игрок провел две игры, то его суммарное вознаграждение состоит из сумма вознаграждений за каждую из игр
Мы представляем фичи модели в качестве игроков, а призовой фонд — как итоговое предсказание модели.
Рассмотрим пример
Формула для расчета значения Шэпли для i-той фичи:
Здесь:
— это предсказание модели с i-той фичей,
— это предсказание модели без i-той фичи,
— количество фичей,
— произвольный набор фичей без i-той фичи
Значение Шэпли для i-той фичи рассчитывается для каждого сэмпла данных (например, для каждого клиента в выборке) на всех возможных комбинациях фичей (включая отсутствие всех фичей), затем полученные значения суммируются по модулю и получается итоговая важность i-той фичи.
Данные вычисления чрезвычайно затратны, поэтому под капотом используются различные алгоритмы оптимизации вычислений, подробнее можно посмотреть по ссылке выше на гитхабе.
Возьмём ванильный пример из документации xgboost.

Мы хотим оценить важность фичей для предсказания, нравятся ли человеку компьютерные игры.
В этом примере для простоты у нас есть две фичи: age (возраст) и gender (пол). Gender (пол) принимает значения 0 и 1.
Возьмём Bobby (маленький мальчик в самом левом узле дерева) и посчитаем значение Шэпли для фичи age (возраст).
У нас есть два набора фичей S:
— нет фичей,
— есть только фича пол.
Ситуация, когда нет значений фичей
Разные модели по-разному работают с ситуациями, когда для сэмпла данных нет фичей, то есть для всех фичей значения равны NULL.
Будет считать в данному случае, что модель усредняет предсказания по веткам дерева, то есть предсказание без фичей будет .
Если же мы добавим знание возраста, то предсказание модели будет .
В итоге значение Шэпли для случая отсутствия фичей:
Ситуация, когда знаем пол
Для Bobby для предсказание без фичи возраст, только с фичей пол, равно . Если же мы знаем возраст, то предсказание — это самое левое дерево, то есть 2.
В итоге значение Шэпли для этого случая:
Суммируем
Итогое значение Шэпли для фичи age (возраст):
Реальный пример из бизнеса
Библиотека SHAP обладает богатым функционалом визуализации, который помогает легко и просто объяснить модель как для бизнеса, так и для самого аналитика, чтобы оценить адекватность модели.
На одном из проектов я анализировал отток сотрудников из компании. В качестве модели использовался xgboost.
Код в python:
import shap
shap_test = shap.TreeExplainer(best_model).shap_values(df)
shap.summary_plot(shap_test, df,
max_display=25, auto_size_plot=True)
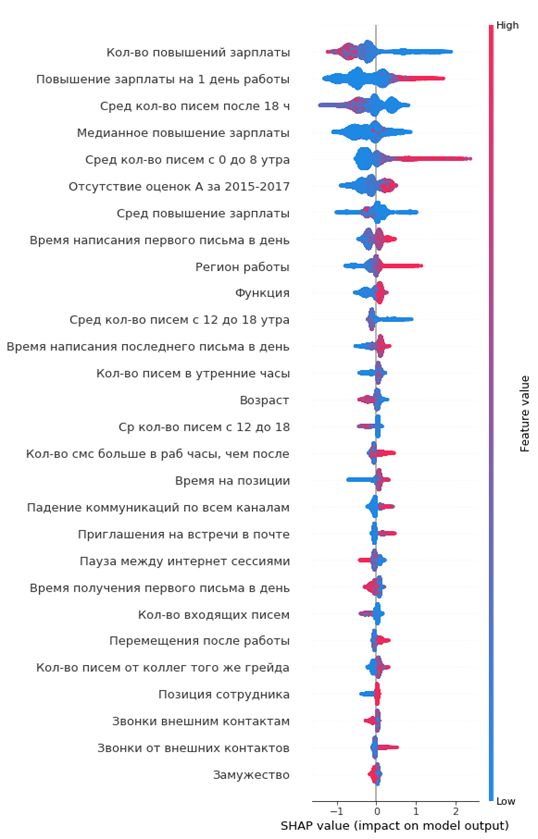
Получившийся график важности фичей:

Как его читать:
- значения слева от центральной вертикальной линии — это negative класс (0), справа — positive (1)
- чем толще линия на графике, тем больше таких точек наблюдения
- чем краснее точки на графике, тем выше значения фичи в ней
Из графика можно сделать интересные выводы и проверить их адекватность:
- чем меньше сотруднику повышают зарплату, тем выше вероятность его ухода
- есть регионы офисов, где отток выше
- чем моложе сотрудник, тем выше вероятность его ухода
- ...
Можно сразу сформировать портрет уходящего сотрудника: eму не повышали зарплату, он достаточно молод, холост, долгое время на одной позиции, не было повышений грейда, не было высоких годовых оценок, он стал мало общаться с коллегами.
Просто и удобно!
Можно объяснить предсказание для конкретного сотрудника:

Или посмотреть зависимость предсказаний от конкретной фичи в виде 2D графика:

Можно визуализировать даже предсказания нейронных сетей на картинках:

Заключение
Я сам узнал о SHAP значениях около полугода назад и это полностью заменило другие методы оценки важности фичей.
Главные преимущества:
- удобные визуализация и интерпретация
- честный расчет важности фичей
- возможность оценить фичи для конкретной подвыборки данных (например, чем отличаются наши покупатели от других клиентов в выборке), делается простым фильтром датасета в pandas и его анализом в shap, буквально пара строчек кода

