Резервуарная выборка (eng. «reservoir sampling») — это простой и эффективный алгоритм случайной выборки некоторого количества элементов из имеющегося вектора большого и/или неизвестного заранее размера. Я не нашел об этом алгоритме ни одной статьи на Хабре и поэтому решил написать её сам.
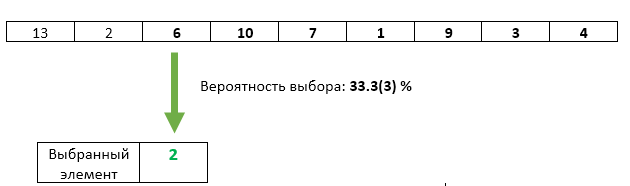
Итак, о чём же идёт речь. Выбрать один случайный элемент из вектора — это элементарная задача:
Задача «вернуть K случайных элементов из вектора размером N» уже хитрее. Здесь уже можно ошибиться — например, взять K первых элементов (это нарушит требование случайности) или взять каждый из элементов с вероятностью K/N (это нарушит требование взять ровно K элементов). Кроме того, можно реализовать и формально корректное, но крайне неэффективное решение «перемешать случайно все элементы и взять K первых». И всё становится ещё интереснее, если добавить условие того, что N — число очень большое (нам не хватит памяти сохранить все N элементов) и/или не известно заранее. Для примера представим себе, что у нас есть какой-то внешний сервис, присылающий нам элементы по одному. Мы не знаем сколько их придёт всего и не можем сохранить их все, но хотим в любой момент времени иметь набор из ровно K случайно выбранных элементов из уже полученных.
Алгоритм резервуарной выборки позволяет решить эту задачу за O(N) шагов и O(K) памяти. При этом не требуется знать N заранее, а условие случайности выборки ровно K элементов будет чётко соблюдено.
Пусть K=1, т.е. нам нужно выбрать всего один элемент из всех пришедших — но так, чтобы у каждого из пришедших элементов была одинаковая вероятность быть выбранным. Алгоритм напрашивается сам собой:
Шаг 1: Выделяем память на ровно один элемент. Сохраняем в неё первый пришедший элемент.

Пока всё ок — нам пришел всего один элемент, с вероятностью в 100% (на данный момент) он должен являться выбранным — так и есть.
Шаг 2: Второй пришедший элемент с вероятностью 1/2 перезаписываем в качестве выбранного.

Здесь тоже всё хорошо: нам пока пришло только два элемента. Первый остался выбранным с вероятностью 1/2, второй перезаписал его с вероятностью 1/2.
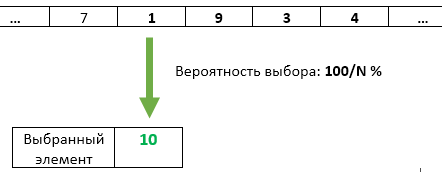
Шаг 3: Третий пришедший элемент с вероятностью 1/3 перезаписываем в качестве выбранного.
С третьим элементом всё хорошо — его шанс быть выбранным равен ровно 1/3. Но не нарушили ли мы каким-либо образом равенство шансов предыдущих элементов? Нет. Вероятность того, что на этом шаге выбранный элемент не будет перезаписан равна 1 — 1/3 = 2/3. А поскольку на шаге 2 мы гарантировали равенство шансов каждого из элементов быть выбранным, то после шага 3 каждый из них может оказаться выбранным с шансом 2/3 * 1/2 = 1/3. Ровно такой же шанс, как и у третьего элемента.
Шаг N: С вероятностью 1/N элемент номер N перезаписываем в качестве выбранного. У каждого из предыдущих пришедших элементов остаётся тот же шанс 1/N остаться выбранным.
Но это была упрощённая задача, при K=1.
Шаг 1: Выделяем память на K элементов. Записываем в неё первые K пришедших элементов.

Единственный способ взять K элементов из K пришедших элементов — это взять их все :)
Шаг N: (для каждого N > K): генерируем случайное число X от 1 до N. Если X > K то отбрасываем данный элемент и переходим к следующему. Если X <= K, то перезаписываем элемент под номером X. Поскольку значение X будет равномерно случайно на диапазоне от 1 до N, то при условии X <= K оно будет равномерно случайно и на диапазоне от 1 до K. Таким образом мы обеспечиваем равномерность выбора перезаписываемых элементов.

Как можно заметить — каждый следующий пришедший элемент имеет всё меньшую и меньшую вероятность быть выбранным. Она, тем ни менее, всегда будет равна ровно K/N (как и для каждого из предыдущих пришедших элементов).
Плюс этого алгоритма в том, что мы можем в любой момент времени остановиться, показать пользователю текущий вектор K — и это будет вектор честно выбранных случайных элементов из пришедшей последовательности элементов. Возможно, пользователя это устроит, а возможно, он захочет продолжить обработку входящих значений — мы можем это сделать в любой момент. При этом, как упоминалось в начале, мы никогда не используем больше, чем О(K) памяти.
Ах да, совсем забыл, в стандартную библиотеку С++17 наконец вошла функция std::sample, делающая ровно то, что описано выше. Стандарт не обязывает её использовать именно резервуарную выборку, но обязывает работать за O(N) шагов — ну и вряд ли разработчики её реализации в стандартной библиотеке выберут какой-то алгоритм, использующий более, чем О(K) памяти (а меньше тоже не получится — результат же нужно где-то хранить).
Итак, о чём же идёт речь. Выбрать один случайный элемент из вектора — это элементарная задача:
// C++
std::random_device rd;
std::mt19937 gen(rd());
std::uniform_int_distribution<> dis(0, vect.size() — 1);
auto result = vect[dis(gen)];
Задача «вернуть K случайных элементов из вектора размером N» уже хитрее. Здесь уже можно ошибиться — например, взять K первых элементов (это нарушит требование случайности) или взять каждый из элементов с вероятностью K/N (это нарушит требование взять ровно K элементов). Кроме того, можно реализовать и формально корректное, но крайне неэффективное решение «перемешать случайно все элементы и взять K первых». И всё становится ещё интереснее, если добавить условие того, что N — число очень большое (нам не хватит памяти сохранить все N элементов) и/или не известно заранее. Для примера представим себе, что у нас есть какой-то внешний сервис, присылающий нам элементы по одному. Мы не знаем сколько их придёт всего и не можем сохранить их все, но хотим в любой момент времени иметь набор из ровно K случайно выбранных элементов из уже полученных.
Алгоритм резервуарной выборки позволяет решить эту задачу за O(N) шагов и O(K) памяти. При этом не требуется знать N заранее, а условие случайности выборки ровно K элементов будет чётко соблюдено.
Начнём с упрощённой задачи
Пусть K=1, т.е. нам нужно выбрать всего один элемент из всех пришедших — но так, чтобы у каждого из пришедших элементов была одинаковая вероятность быть выбранным. Алгоритм напрашивается сам собой:
Шаг 1: Выделяем память на ровно один элемент. Сохраняем в неё первый пришедший элемент.

Пока всё ок — нам пришел всего один элемент, с вероятностью в 100% (на данный момент) он должен являться выбранным — так и есть.
Шаг 2: Второй пришедший элемент с вероятностью 1/2 перезаписываем в качестве выбранного.

Здесь тоже всё хорошо: нам пока пришло только два элемента. Первый остался выбранным с вероятностью 1/2, второй перезаписал его с вероятностью 1/2.
Шаг 3: Третий пришедший элемент с вероятностью 1/3 перезаписываем в качестве выбранного.

С третьим элементом всё хорошо — его шанс быть выбранным равен ровно 1/3. Но не нарушили ли мы каким-либо образом равенство шансов предыдущих элементов? Нет. Вероятность того, что на этом шаге выбранный элемент не будет перезаписан равна 1 — 1/3 = 2/3. А поскольку на шаге 2 мы гарантировали равенство шансов каждого из элементов быть выбранным, то после шага 3 каждый из них может оказаться выбранным с шансом 2/3 * 1/2 = 1/3. Ровно такой же шанс, как и у третьего элемента.
Шаг N: С вероятностью 1/N элемент номер N перезаписываем в качестве выбранного. У каждого из предыдущих пришедших элементов остаётся тот же шанс 1/N остаться выбранным.

Но это была упрощённая задача, при K=1.
Как изменится алгоритм при K>1 ?
Шаг 1: Выделяем память на K элементов. Записываем в неё первые K пришедших элементов.

Единственный способ взять K элементов из K пришедших элементов — это взять их все :)
Шаг N: (для каждого N > K): генерируем случайное число X от 1 до N. Если X > K то отбрасываем данный элемент и переходим к следующему. Если X <= K, то перезаписываем элемент под номером X. Поскольку значение X будет равномерно случайно на диапазоне от 1 до N, то при условии X <= K оно будет равномерно случайно и на диапазоне от 1 до K. Таким образом мы обеспечиваем равномерность выбора перезаписываемых элементов.

Как можно заметить — каждый следующий пришедший элемент имеет всё меньшую и меньшую вероятность быть выбранным. Она, тем ни менее, всегда будет равна ровно K/N (как и для каждого из предыдущих пришедших элементов).
Плюс этого алгоритма в том, что мы можем в любой момент времени остановиться, показать пользователю текущий вектор K — и это будет вектор честно выбранных случайных элементов из пришедшей последовательности элементов. Возможно, пользователя это устроит, а возможно, он захочет продолжить обработку входящих значений — мы можем это сделать в любой момент. При этом, как упоминалось в начале, мы никогда не используем больше, чем О(K) памяти.
Ах да, совсем забыл, в стандартную библиотеку С++17 наконец вошла функция std::sample, делающая ровно то, что описано выше. Стандарт не обязывает её использовать именно резервуарную выборку, но обязывает работать за O(N) шагов — ну и вряд ли разработчики её реализации в стандартной библиотеке выберут какой-то алгоритм, использующий более, чем О(K) памяти (а меньше тоже не получится — результат же нужно где-то хранить).
Материалы по теме
- Доклад разработчика из Facebook о том, как резервуарная выборка была использована в их движке поиска по внутренней кодовой базе (с 34-ой минуты).
- Статья в Википедии
- std::sample на Cppreference
Комментарии (20)

vibornoff
30.11.2018 16:20Итак, о чём же идёт речь. Выбрать один случайный элемент из вектора — это элементарная задача:
И это, разумеется, не совсем правда.
auto result = vect[rand() % vect.size()]; // С++
Не будем рассматривать тривиальный случай, когдаRAND_MAX < vect.size().
Так вот, правдой оно будет тогда и только тогда, когдаvect.size() % RAND_MAX == 0.
Для всех остальных случаев значения из диапазона[0 ... vect.size() % RAND_MAX)будут возвращаться немножечко чаще.
Например, в векторе у нас 2 элемента, а RAND_MAX равен 3. Тогда первый элемент вектора будет возвращатся вдвое чаще второго.
tangro Автор
30.11.2018 16:43Всё так! Спасибо!
Как на счёт вот такого кода:
std::random_device rd;
std::mt19937 gen(rd());
std::uniform_int_distribution<> dis(0, vect.size() — 1);
auto result = vect[dis(gen)];
Это будет работать лучше, верно?

AngReload
01.12.2018 08:26-1Считается ли такой вариант как K шагов и 2K дополнительной памяти?
JavaScriptfunction rnd_int_less(n) { return Math.floor(Math.random() * n); } function reservoir_sampling(k, n_arr) { let n = n_arr.length; let k_arr = []; let j_arr = []; // shuffle for (let i = 0; i < k; i++) { const j = i + rnd_int_less(n - i); j_arr.push(j); const a = n_arr[i]; const b = n_arr[j]; k_arr[i] = b; n_arr[i] = b; n_arr[j] = a; } // unshuffle for (let i = k - 1; i >= 0; i--) { const j = j_arr[i]; const a = n_arr[i]; const b = n_arr[j]; n_arr[i] = b; n_arr[j] = a; } return k_arr; }


Akon32
Я правильно понимаю, что если у нас (например) при K=3 последовательность
1,2,3,1,2,3,1,2,3,..., то из-за размещения элементов по правилу N%K мы не имеем шанса получить в выходной выборке больше одной единицы (а также больше одной двойки и одной тройки)?Как это согласуется с утверждением:
..? Мне кажется, выбор элементов будет частично неслучаен (коллизии элементов на расстоянии K друг от друга), что проявится в некоторых случаях (как в моём примере).
rafuck
В примере, похоже, ошибка и 10 (четвертый элемент посл-ти) должна заменить не 13 (первый элемент в резервуаре), а двойку (второй элемент). Метод вычисления индекса на замену (N%K) предполагает, что индексация резервуара начинается с нуля. Но, тем не менее, похоже вы правы, в вашем примере после первых трех шагов получается выборка [1,2,3], а после четвертого шага либо [1,2,3] (новый элемент не попал в выборку), либо [1,1,3] — новый элемент попал в выборку. Вариант [1,2,1], видимо, невозможен.
mayorovp
На самом деле алгоритм требует случайного равномерного выбора заменяемого элемента.
tangro Автор
Это так. И этот вопрос интересно обсуждается вот в этом видео начиная с момента 41:07. Автор говорит убедительно, но есть один хитрый момент: он утверждает, что random() % N даёт равномерное распределение от 0 до N, а значит нам достаточно его одного и для решения, брать ли элемент и для определения его позиции.
Начать нужно с того, что вообще чёрт его знает, что такое random() — в стандарте С++ есть только rand(), а значит random() — это какой-то их собственный фейсбучный велосипед и не известно, как он работает. Без этого знания было бы действительно надёжнее сгенерировать второе случайное число.
С другой стороны, пример на R в Википедии тоже обходится одним random'oм — но это принципиально другая функция, генерирующая случайное число по равномерному распределению между двумя заданными. Тут действительно, достаточно его одного и для решения брать ли число (J < K) и для использование его в качестве индекса (распределение между 1 и K будет настолько же равномерным, как и между 1 и N).
mayorovp
Одного случайного числа и правда достаточно (до тех пор пока N << RAND_MAX), это и без видео понятно.
Вот только правильный алгоритм выглядит так:
А у вас — вот такой алгоритм получился:
Откуда тут взялось число N%K?
tangro Автор
Вопрос с N << RAND_MAX решился исправлением кода в первом примере на более корректный — давайте будем считать, что мы генерируем числа в диапазоне от 1 до N именно так :)
На счёт N%K — я хотел упростить, но, видимо, сам себя запутал. Имелось в виду значение X%K, что для рассматриваемого случая X < K вырождается в просто Х.
Сейчас поправлю, спасибо.
Akon32
Да, теперь похоже на правду.
arabesc
Например, при RAND_MAX == 2 и N == 2 вероятность выпадения 0 составит 2/3, а для 1 будет 1/3.
p.s. вижу, дальше в комментариях об этом уже написали
tangro Автор
Алгоритм ничего не знает о значении элементов. Для него та единица, которая в этой последовательности первая и та, которая четвёртая — это два разных элемента, равны они или не равны — роли не играет. И всё, что он гарантирует, что и первая единица, и четвёртая имеют равные шансы попасть в результирующую выборку на любом шаге алгоритма. При этом никто не даёт никаких гарантий их туда одновременного попадания.
Akon32
Но они не могут попасть в выборку одновременно.
Более наглядный пример: последовательность
1,2,3,4,5,6,7,8,9, K=3.Невозможно получить выборку, в которой содержатся одновременно элементы 1 и 4 (это конкретный пример, один из многих).
Т.е., в общем виде, при условии наличия в выборке элемента с номером i вероятность наличия в выборке других элементов с номером (i % K) равна 0. Такие элементы, с равными по модулю K индексами, друг друга вытесняют из выборки, но при этом они не вытесняют остальные элементы.
HappyLynx
И все же, под взятием K случайных элементов из множества X обычно подразумевается, что если мы возьмем множество всех подмножеств мощности K множества X, то функция вероятности того, что какое-либо из данных подмножеств будет результатом выборки, должна иметь равномерное распределение.
И Akon32 вполне обоснованно показывает, что описанный алгоритм не обеспечивает данной равномерности, т.к. на модельном множестве некоторые из подмножеств элементов (вне зависимости от их значения) мощности K имеют нулевую вероятность оказаться результатом работы алгоритма. Например (при нумерации с 0 и K = 2), вероятность одновременного попадания в результат элементов с номерами 0 и 2 равна нулю.
Цитата из ветки выше:
> Автор говорит убедительно, но есть один хитрый момент: он утверждает, что random() % N даёт равномерное распределение от 0 до N, а значит нам достаточно его одного и для решения, брать ли элемент и для определения его позиции.
Автор очень лихо оставляет незамеченным тот факт, что вид распределения абсолютно ничего не говорит о взаимной независимости случайных величин. А они у него получаются зависимыми, более того, f1(x) = f2(x).
tangro Автор
Akon32 был прав и статья была исправлена, чтобы отразить этот момент.