Привет, Хабр! Представляю вашему вниманию перевод статьи «Everything you need to know about Scatter Plots for Data Visualisation» автора George Seif.
Если вы занимаетесь анализом и визуализацией данных, то скорее Вам придется столкнуться с точечными диаграммами. Несмотря на свою простоту, точечные диаграммы являются мощным инструментом для визуализации данных. Манипулируя цветами, размерами и формами можно обеспечить гибкость и репрезентативность точечных диаграмм.
В этой статье вы узнаете практически все, что вам необходимо знать о визуализации данных используя точечные диаграммы. Мы постараемся разобрать все необходимые параметры в их использовании в коде python. Также вы можете найти несколько практических уловок.
Даже самое примитивное использование точечной диаграммы уже дает сносный обзор наших данных. На рисунке 1 мы уже можем видеть островки объединённых данных и быстро выделить выбросы.
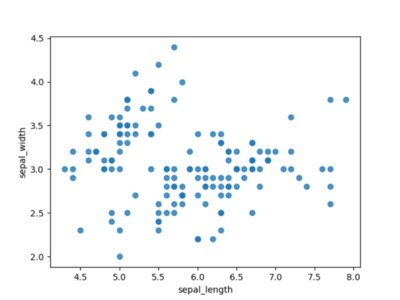
Рисунок 1
Уместно проведенные регрессионные линий визуально упрощает задачу выявления точек, близких к середине. На рисунке 2 мы провели линейный график. Довольно легко увидеть, что в данном случае линейная функция не репрезентативен, так как многие точки находятся довольно далеко от линии.

Рисунок 2
Рисунок 3 использует полином порядка 4 и выглядит гораздо более многообещающе. Похоже, что для моделирования этого набора данных нам определенно понадобится полином порядка 4.
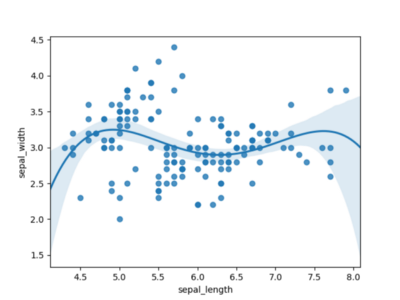
Рисунок 3
Цвет и форму можно использовать для визуализации различных категорий в вашем наборе данных. Цвет и форма визуально очень понятны. Когда вы смотрите на график, где группы точек имеют разные цвета наших фигур, сразу становится очевидным, что точки принадлежат разным группам.
На рисунке 4 показаны классы, сгруппированные по цвету. На рисунке 5 показаны классы, разделенные по цвету и форме. В обоих случаях намного легче увидеть группировку. Теперь мы знаем, что будет легко отделить класс setosa, и на что мы должны сосредоточить внимание. Также ясно, что один линейный график не сможет разделить зеленую и оранжевую точки. Поэтому нам нужно добавить что-то для отображения больше измерений.
Выбор между цветом и формой становится вопросом предпочтения. Лично я нахожу цвет немного более четким и интуитивно понятным, но выбор остается всегда за Вами.
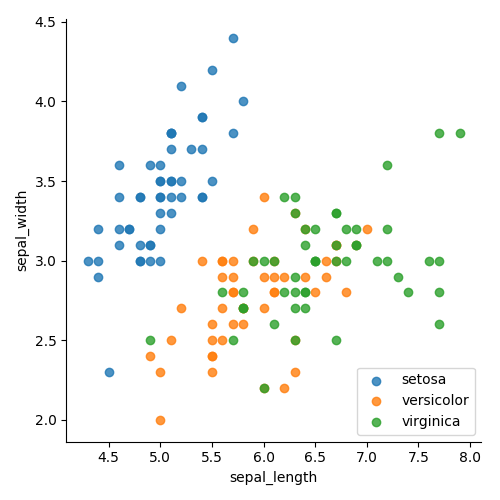
Рисунок 4

Рисунок 5
Пример графика с маргинальными гистограммами показан на рисунке 6. Маргинальные гистограммы наложены сверху и сбоку, представляют собой распределение точек для объектов вдоль абсциссы и ординате. Это небольшое дополнение отлично подходит для более точного определения распределения точек и выбросов.
Например, на рисунке 6 мы очевидно видим высокую концентрацию точек около разметки 3,0. И благодаря этой гистограмме можно определить уровень концентрации. В правом боку видно, что вокруг разметки 3,0 есть как минимум втрое больше точек, чем для любого другого дискретного диапазона. Также с помощью правой боковой гистограммы можно с очевидностью распознать, что очевидные выбросы находятся выше отметки 3,75. По верхней диаграмме видно, что распределение точек по оси Х является более равномерным, за исключением выбросов в крайнем правом углу.
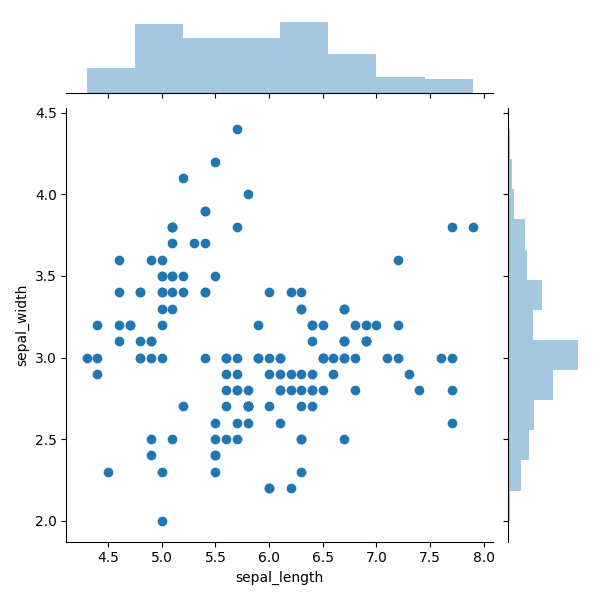
Рисунок 6
С помощью пузырьковых диаграмм нам необходимо использовать несколько переменных для кодирования информации. Новым параметром, свойственный для этого вида визуализацией, является размер. На рисунке 7 мы показываем количество съеденного картофеля фри разрезе роста и веса съевших людей. Обратите внимание, что точечная диаграмма — это всего лишь инструмент двухмерной визуализации, но при использовании пузырьковых диаграмм мы умело можем отображать информацию с тремя измерениями.
Здесь мы используем цвет, положение и размер, где положение пузырьков определяет рост и вес человека, цвет определяет пол, а размер определяется количеством съеденной картошки фри. Пузырьковая диаграмма с легкостью позволяет нам удобно объединить все атрибуты в один график, чтобы мы могли видеть информацию большого размера в двухмерном виде.

Рисунок 7
Если вы занимаетесь анализом и визуализацией данных, то скорее Вам придется столкнуться с точечными диаграммами. Несмотря на свою простоту, точечные диаграммы являются мощным инструментом для визуализации данных. Манипулируя цветами, размерами и формами можно обеспечить гибкость и репрезентативность точечных диаграмм.
В этой статье вы узнаете практически все, что вам необходимо знать о визуализации данных используя точечные диаграммы. Мы постараемся разобрать все необходимые параметры в их использовании в коде python. Также вы можете найти несколько практических уловок.
Построение регрессии
Даже самое примитивное использование точечной диаграммы уже дает сносный обзор наших данных. На рисунке 1 мы уже можем видеть островки объединённых данных и быстро выделить выбросы.

Рисунок 1
Уместно проведенные регрессионные линий визуально упрощает задачу выявления точек, близких к середине. На рисунке 2 мы провели линейный график. Довольно легко увидеть, что в данном случае линейная функция не репрезентативен, так как многие точки находятся довольно далеко от линии.

Рисунок 2
Рисунок 3 использует полином порядка 4 и выглядит гораздо более многообещающе. Похоже, что для моделирования этого набора данных нам определенно понадобится полином порядка 4.

Рисунок 3
import seaborn as sns
import matplotlib.pyplot as plt
df = sns.load_dataset('iris')
# A regular scatter plot
sns.regplot(x=df["sepal_length"], y=df["sepal_width"], fit_reg=False)
plt.show()
# A scatter plot with a linear regression fit:
sns.regplot(x=df["sepal_length"], y=df["sepal_width"], fit_reg=True)
plt.show()
# A scatter plot with a polynomial regression fit:
sns.regplot(x=df["sepal_length"], y=df["sepal_width"], fit_reg=True, order=4)
plt.show()Цвет и форма точек
Цвет и форму можно использовать для визуализации различных категорий в вашем наборе данных. Цвет и форма визуально очень понятны. Когда вы смотрите на график, где группы точек имеют разные цвета наших фигур, сразу становится очевидным, что точки принадлежат разным группам.
На рисунке 4 показаны классы, сгруппированные по цвету. На рисунке 5 показаны классы, разделенные по цвету и форме. В обоих случаях намного легче увидеть группировку. Теперь мы знаем, что будет легко отделить класс setosa, и на что мы должны сосредоточить внимание. Также ясно, что один линейный график не сможет разделить зеленую и оранжевую точки. Поэтому нам нужно добавить что-то для отображения больше измерений.
Выбор между цветом и формой становится вопросом предпочтения. Лично я нахожу цвет немного более четким и интуитивно понятным, но выбор остается всегда за Вами.

Рисунок 4

Рисунок 5
import seaborn as sns
import matplotlib.pyplot as plt
df = sns.load_dataset('iris')
# Use the 'hue' argument to provide a factor variable
sns.lmplot( x="sepal_length", y="sepal_width", data=df, fit_reg=False, hue='species', legend=False)
plt.legend(loc='lower right')
plt.show()
sns.lmplot( x="sepal_length", y="sepal_width", data=df, fit_reg=False, hue='species', legend=False, markers=["o", "P", "D"])
plt.legend(loc='lower right')
plt.show()Маргинальная гистограмма
Пример графика с маргинальными гистограммами показан на рисунке 6. Маргинальные гистограммы наложены сверху и сбоку, представляют собой распределение точек для объектов вдоль абсциссы и ординате. Это небольшое дополнение отлично подходит для более точного определения распределения точек и выбросов.
Например, на рисунке 6 мы очевидно видим высокую концентрацию точек около разметки 3,0. И благодаря этой гистограмме можно определить уровень концентрации. В правом боку видно, что вокруг разметки 3,0 есть как минимум втрое больше точек, чем для любого другого дискретного диапазона. Также с помощью правой боковой гистограммы можно с очевидностью распознать, что очевидные выбросы находятся выше отметки 3,75. По верхней диаграмме видно, что распределение точек по оси Х является более равномерным, за исключением выбросов в крайнем правом углу.

Рисунок 6
import seaborn as sns
import matplotlib.pyplot as plt
df = sns.load_dataset('iris')
sns.jointplot(x=df["sepal_length"], y=df["sepal_width"], kind='scatter')
plt.show()Пузырьковые диаграммы
С помощью пузырьковых диаграмм нам необходимо использовать несколько переменных для кодирования информации. Новым параметром, свойственный для этого вида визуализацией, является размер. На рисунке 7 мы показываем количество съеденного картофеля фри разрезе роста и веса съевших людей. Обратите внимание, что точечная диаграмма — это всего лишь инструмент двухмерной визуализации, но при использовании пузырьковых диаграмм мы умело можем отображать информацию с тремя измерениями.
Здесь мы используем цвет, положение и размер, где положение пузырьков определяет рост и вес человека, цвет определяет пол, а размер определяется количеством съеденной картошки фри. Пузырьковая диаграмма с легкостью позволяет нам удобно объединить все атрибуты в один график, чтобы мы могли видеть информацию большого размера в двухмерном виде.

Рисунок 7
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
x = np.array([100, 105, 110, 124, 136, 155, 166, 177, 182, 196, 208, 230, 260, 294, 312])
y = np.array([54, 56, 60, 60, 60, 72, 62, 64, 66, 80, 82, 72, 67, 84, 74])
z = (x*y) / 60
for index, val in enumerate(z):
if index < 10:
color = 'g'
else:
color = 'r'
plt.scatter(x[index], y[index], s=z[index]*5, alpha=0.5, c=color)
red_patch = mpatches.Patch(color='red', label='Male')
green_patch = mpatches.Patch(color='green', label='Female')
plt.legend(handles=[green_patch, red_patch])
plt.title("French fries eaten vs height and weight")
plt.xlabel("Weight (pounds)")
plt.ylabel("Height (inches)")
plt.show()

boogiebomzh
Человеку довольно сложно определить разницу в площади пузырьков, поскольку она изменяется нелинейно. Поэтому значения желательно указывать еще и цифрами на пузырьках.