
Весна в самом разгаре, последний снег практически везде растаял и воцарилось долгожданное тепло. Теплолюбивые люди наконец-то начинают снимать с себя вязаные свитера, шарфы и шапки, а моржи уже вовсю разгуливают в шортах и майках. Тем временем в одной из лабораторий университета Вены царит собачий холод и ученые тому чрезвычайно рады, ибо по-другому исследовать квантовые эффекты наночастиц крайне сложно. Если без литературных оборотов, то сегодня мы познакомимся с практическим испытанием нового метода охлаждения левитирующей наночастицы посредством ловушки из оптического резонатора. Зачем и как ученые заморозили наночастицу практически до абсолютного нуля, насколько действенен их метод и что он может привнести в изучение квантовых эффектов? Ответы на эти и другие вопросы мы найдем в докладе исследовательской группы. Поехали.
Основа эксперимента
Лазерное улавливание частиц и их охлаждение является одним из весьма популярных инструментов в атомной физике, как говорят сами ученые, и с ними сложно не согласиться. Если опустить все супер-пупер сложные формулировки от которых волосы встанут дыбом даже там, где их вроде и нет, то весь процесс можно описать следующим образом: двигательное охлаждение атома или молекулы возможно за счет полного отказа от поглощения доплеровски-смещенных лазерных фотонов и последующего самопроизвольного излучения. Но этот процесс зависит от внутренней структуры охлаждаемой частицы. Избежать этой зависимости можно посредством объединения движения частицы и поля оптического резонатора, что в результате даст новую схему охлаждения.
Большой интерес в исследовательских кругах получил метод резонаторного охлаждения посредством когерентного рассеяния поля оптической ловушки. В такой ситуации управляемый диполь производит рассеяние, которое когерентно с полем возбуждения. Рассеяние фотонов в изначально пустом оптическом резонаторе и предоставляет новый метод охлаждения. Если применить правильную лазерную расстройку поля возбуждения от резонатора, то можно резонансно усилить процесс рассеяния, что в свою очередь ликвидирует энергию от движения частиц. Именно удаление этой энергии и есть охлаждение.
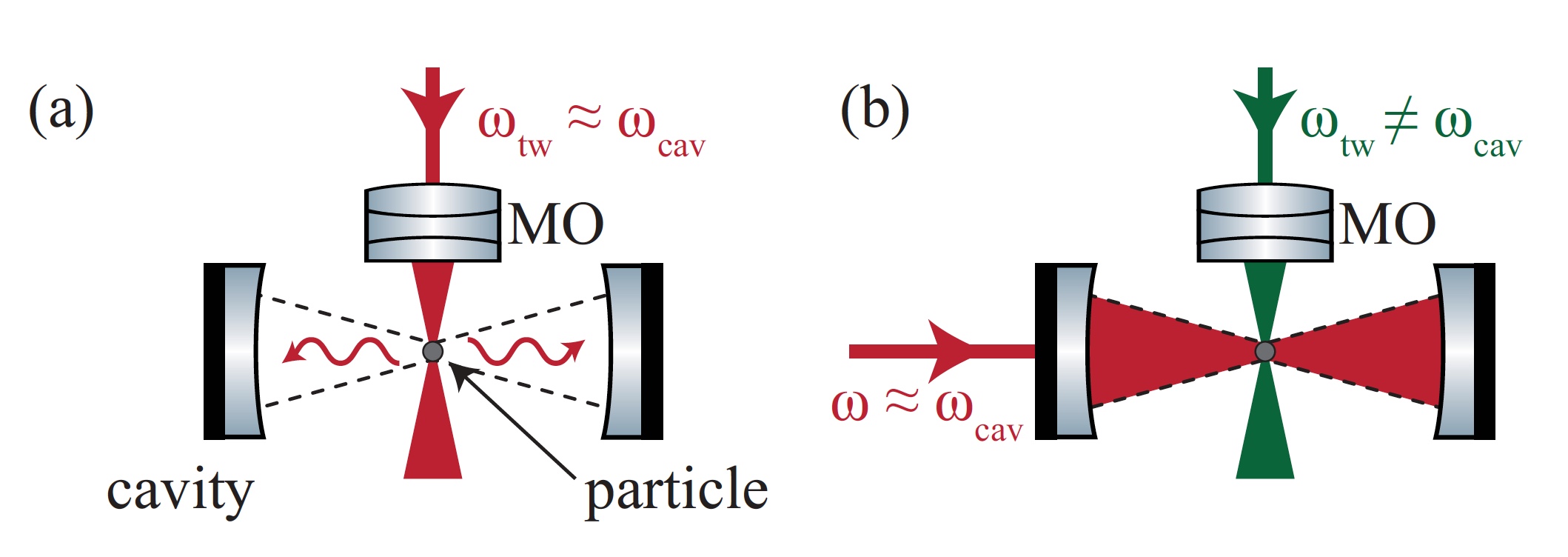
Изображение№1: два варианта резонаторного охлаждения левитирующей частицы.
На изображении 1а показано, что резонаторное охлаждение посредством когерентного рассеяния от оптических ловушек (иногда «пинцетов») основано на дипольном излучении, испускаемого в пустой оптический резонатор.
Изображение 1b — в стандартной дисперсионной оптомеханике внешний лазер управляет как резонатором так и рассеянием. Оптимальное охлаждение возможно при наибольшем градиенте интенсивности моды резонатора.
В своей работе ученые продемонстрировали практическую реализацию резонаторного охлаждения левитирующей наночастицы посредством когерентного рассеяния. При этом ученым удалось провести данный процесс в трех направлениях теплового движения, тогда как ранее подобные эксперименты успешно проводились только в одном направлении и только с атомами в качестве испытуемых.
Теоретическая база
Кто любит красивые формулы, напоминающие бабушкино кружево, сейчас мы парочку таких рассмотрим.
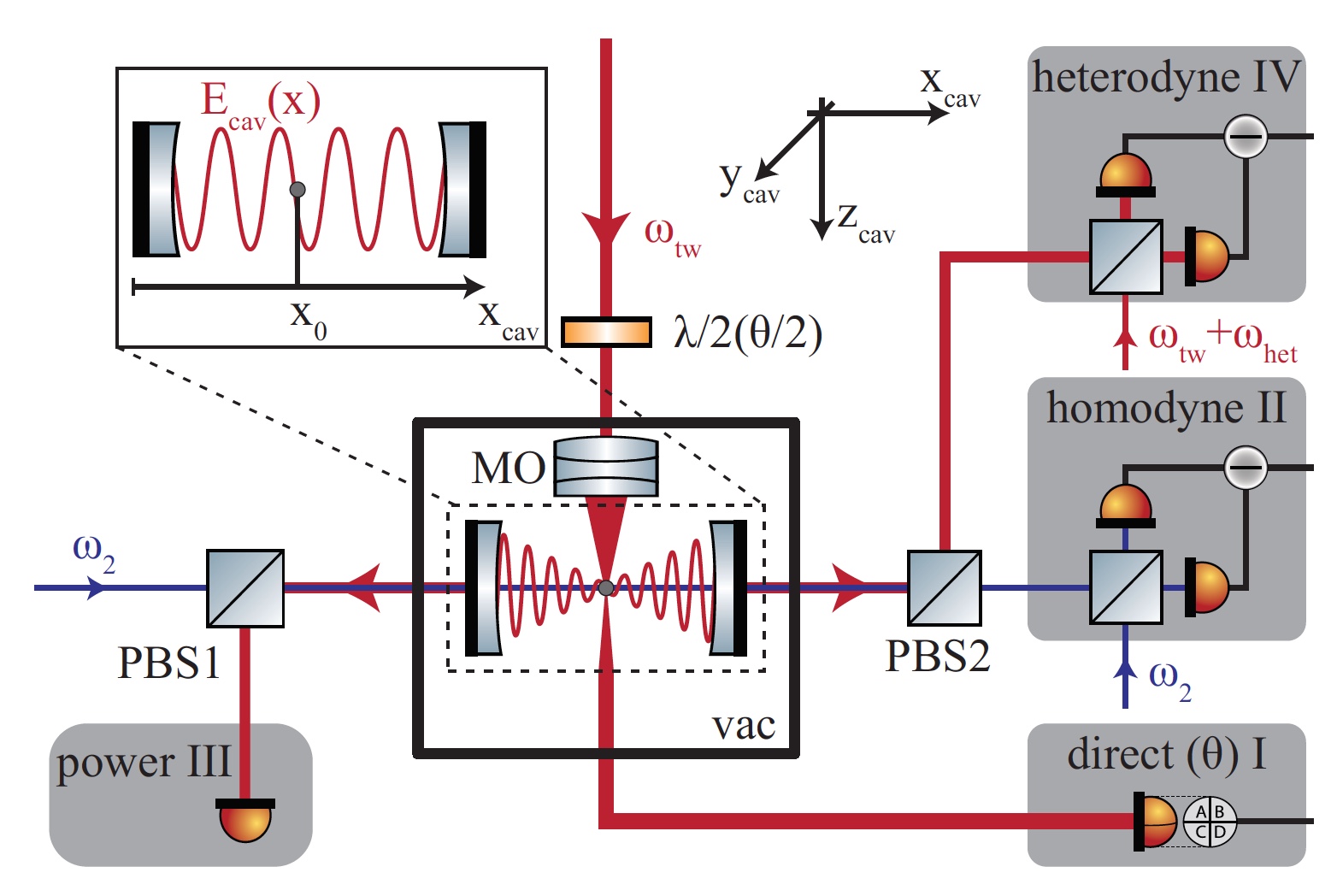
Изображение №2: схема резонаторного охлаждения посредством когерентного рассеяния.
Оптическая ловушка формируется за счет лазера с частотой ?t?, который сфокусирован объективом микроскопа (ОМ) внутрь вакуумной камеры (vac). Наночастица левитирует в центре резонатора Фабри—Перо. Слабый блокирующий луч выводится из улавливающего лазера и резонаторно управляет оптическим резонатором на частоте ?2, позволяя стабильно зафиксировать ?t? и ?2 относительно частоты оптического резонатора. PBS на изображении выше это поляризационный разделитель лучей, а ?het — частота гетеродинной демодуляции.
А теперь рассмотрим наночастицу, пойманную лазерным пинцетом с горловинами пучка (Wx;y, самая узкая часть лазерного луча) внутри пустого оптического резонатора при модовом объеме Vcav (горловина пучка w0) и в положении x0 вдоль оси резонатора (изображение №2).
В таком случае взаимодействие между индуцированным диполем и внутренним (локальным) электрическим полем можно описать в виде следующего гамильтониана:
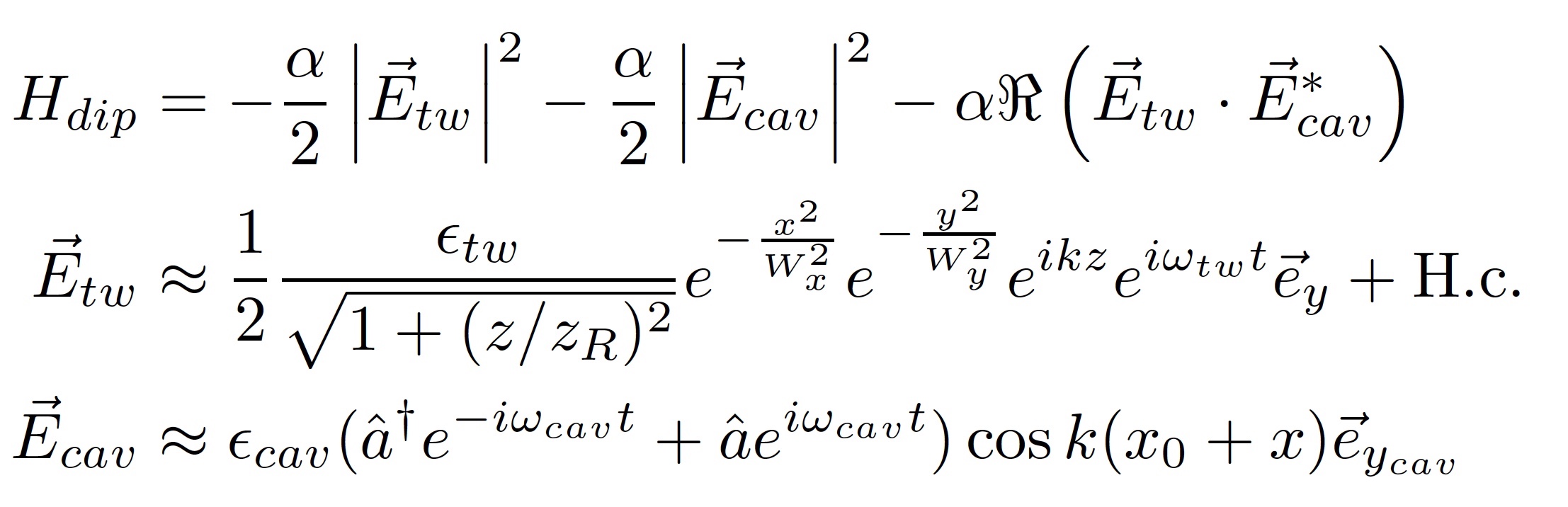
Обозначения:
Etw и Ecav — электрические поля моды пинцета и резонатора;
?tw — частота пинцета;
?cav — частота резонатора;
? — поляризуемость частиц;
a† и a- операторы поля резонатора;
?0 — электрическая постоянная;
с — скорость света;
k — волновое число;
zR — Рэлеевская длина.
Когда частота пинцета приближается к резонансу оптического резонатора, плотность моды резонатора может изменить спектр излучения диполя, что приводит к резонаторно усиленному когерентному рассеянию.
Подобное рассеяние имеет несколько отличительных черт. Во-первых, ввиду направленности рассеянного дипольного излучения сила взаимодействия очень зависит от поляризации улавливающего лазера. Во-вторых, данное взаимодействие будет усиливаться параллельно напряженности поля как оптической ловушки так и резонатора. В-третьих, взаимодействие в электрическом поле резонатора линейно.
Практическая реализация
Как мы видим по схеме на изображении №2, объектив микроскопа и резонатор Фабри—Перо расположены внутри вакуумной камеры. Объектив фокусирует 1064 нм лазер на горловину Wx 0.67 мкм и Wy 0.77 мкм, формируя оптический пинцет (ловушку), который захватывает кварцевую наносферу диаметром 71.5 нм. Ловушка эллиптическая в поперечной плоскости с невырожденными механическими частотами (?x, ?y, ?z)/2? = (190, 170, 38) кГц. Сам объектив закреплен на трехосевом нанопозиционере с шагом в 8 нм. Для контроля над расстройкой между частотами лазера и резонатора, часть света смещается по частоте ?2=?cav-FSR-? и слабо накачивает оптический резонатор. Это обеспечивает фиксирующий сигнал, который позволяет лазерному источнику для оптического пинцета следовать за свободно дрейфующей полостью Фабри-Перо.
В экспериментальной установке имеется 4 канала обнаружения/детектирования (I-IV). Непосредственно обнаружение движения частицы во всех трех направлениях (I), получаемое при рассеянии оптического пинцета. Гомодинное обнаружение пропускания фиксирующего лазера в резонаторе (II), что позволяет получить оптомеханическое обнаружение положения вдоль оси резонатора. Это необходимо для выравнивания частицы относительно поля резонатора без необходимости опираться на когерентно рассеянный свет. Также измерялась и мощность когерентно рассеянных фотонов в оптическом резонаторе (III), параллельно отслеживая утечку поля из левого зеркала резонатора. Четвертым (IV) детектированием является обнаружение излучения из правого зеркала резонатора за счет спектрально разрешенной характеристики фотонов.
Когерентное рассеяние сильно зависит от поляризации оптического пинцета. Ученые проанализировали три варианта рассеяния при следующих линейных углах поляризации: ? = 0, ? = ?/4 и ? = ?/2.
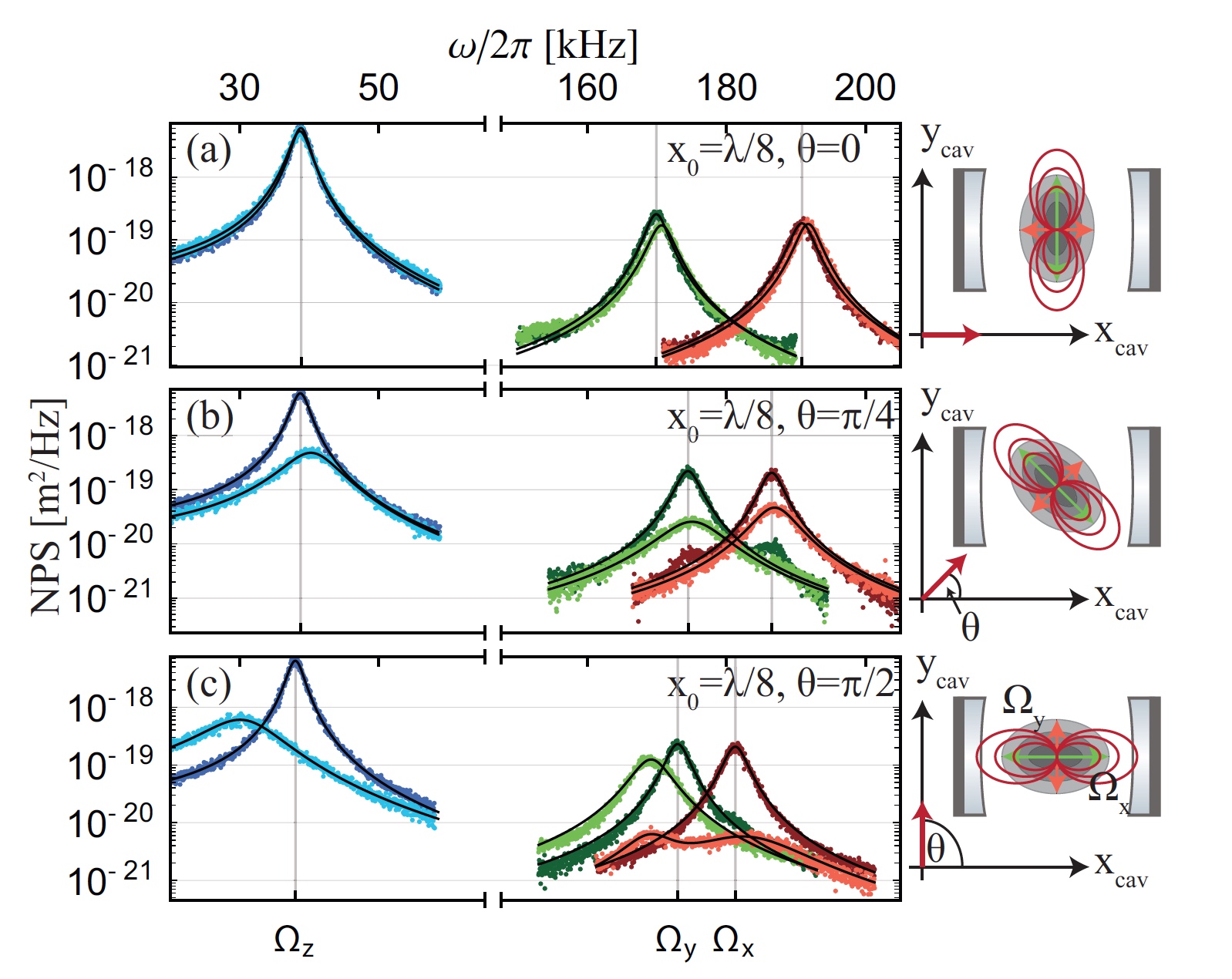
Изображение №3
Сначала поляризация улавливающего лазера была установлена вдоль оси резонатора (т.е. ? = 0), минимизируя рассеяния в моде пустого резонатора (3а). Для идеального выравнивания поляризаций необходимо достичь полного подавления этого рассеяния. Ученым удалось достичь 100-кратного подавления, ограниченного выравниванием между осями пинцета и резонатора. В результате было получено когерентное рассеяние, которое дало незначительное резонаторное охлаждение по осям y и z.
При изменении поляризации на ? = ?/4 ученые наблюдали трехмерное (по всем осям теплового движения) охлаждение посредством когерентного рассеяния (3b). Этот эффект теряется при переходе на поляризацию ? = ?/2. В таком случае наблюдалось неплохое, но все же слабое, охлаждение по осям x и z (3с). Ось y не показывала подобных результатов, что объясняется немного эллиптической формой поляризации ловушки.
Для более детального ознакомления с теорией и практикой данного эксперимента настоятельно рекомендую заглянуть в доклад исследовательской группы.
Эпилог
Суммируя вышесказанное, можно подвести итоги. Наночастица в оптическом пинцете является, так сказать, рассеивателем света во все направления. Если же эту частицу поместить внутри оптического резонатора, то часть этого света может храниться между его зеркалами. Таким образом, фотоны будут рассеиваться внутрь резонатора. Если использовать свет, чья фотонная энергия будет меньше необходимой, то наночастица отдаст часть кинетической энергии, чтобы фотоны могли рассеяться внутри резонатора. А уменьшение кинетической энергии внутри частицы приводит к ее охлаждению.
Одни из авторов сего исследования, Владан Вулетич, уже проводил подобные опыты, но тогда хороших результатов удалось достичь только с использованием атомов и только по одной оси теплового движения.
Данный метод, по словам исследователей, позволит значительно детальнее изучить квантовые свойства тех или иных наночастиц, тем самым расширив наши знания и общее понимание квантового мира и его порой странных и запутанных законов.
Благодарю за внимание, оставайтесь любопытствующими и хорошей всем рабочей недели, ребята.
Спасибо, что остаётесь с нами. Вам нравятся наши статьи? Хотите видеть больше интересных материалов? Поддержите нас оформив заказ или порекомендовав знакомым, 30% скидка для пользователей Хабра на уникальный аналог entry-level серверов, который был придуман нами для Вас: Вся правда о VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps от $20 или как правильно делить сервер? (доступны варианты с RAID1 и RAID10, до 24 ядер и до 40GB DDR4).
VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps до лета бесплатно при оплате на срок от полугода, заказать можно тут.
Dell R730xd в 2 раза дешевле? Только у нас 2 х Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 ТВ от $249 в Нидерландах и США! Читайте о том Как построить инфраструктуру корп. класса c применением серверов Dell R730xd Е5-2650 v4 стоимостью 9000 евро за копейки?


Victor_koly
Упомянутые в формуле «операторы поля резонатора» — это совсем не «операторы рождения» и «операторы уничтожения» для фотонов этого поля?
И, как я понял из формулы №2, гауссов пучок имеет эллиптическое сечение, а не круглое. И ранее упомянуто:
И что-то я совсем забыл, Фабри-Перо — это по определению 2 прямоугольных одинаковых по форме и ориентации зеркала, то есть точно не эллиптические?
mitiaj-b
Интерферометр Фабри-Перо это плоскопаралельные зеркала. А какая у них форма контура дело десятое
Victor_koly
Но тут конкретная мода в форме «эллиптическоя гауссианы»:
exp{-(x/wx)^2-(y/wy)^2}.
Хотя это не соответствует обычным круглым или прямоугольным зеркалам. В них оставался бы член
exp{-(x^2+y^2)/w^2},
умноженный на функцию этих координат.
Например, для плоских зеркал (знаю именно для одинаковых как по форме, так и по ориентации) эта функция умножалась бы на
Hm(21/2x/w)Hn(21/2y/w)
И возможность зеркал поддерживать такие моды с высоким индексом была бы ограничена их размером по соответствующей координате.
Shkaff
Почему прямоугольные-то? В экспериментах круглые обычно, сферические или эллиптические по кривизне.
Victor_koly
Не знаю. Почему-то я думал, что для одних случаев нужны прямоугольные по сечению зеркала, а для других — круглые.
По кривизне — плоские или сферические (конфокальный, полусферический и т.д., с условием, ЕМНИП, ABCD = 0 для матрицы полного прохода резонатора — «туда»+«назад). Или ABCD = 1 для вырожденного резонатора? Точно, 1 должно быть.
Эллиптический можно взять как аналог сферического, или может расположить плоское зеркало в дальнем фокусе.
А ещё я как-то придумал идею, что в определенных случаях радиус зеркала (то есть не радиус кривизны, а радиус „цилиндра“, в который вписаны зеркала) должен быть не больше
r = (lambda*R)1/2, где R — радиус кривизны.
Условно говоря, для 1 метра и 1 мкм это выходит 1 мм, а для 100 метров и 1 мкм — 10 мм.
Следствие — настоящий резонатор Фабри-Перо нужно „полировать“ так, чтобы не вышло „бугорка“ с малым радиусом кривизны. Но может хватит такой „бугорок радиусом кривизны 100 метров“ полировать только в радиусе этих самых 10 мм от оси.
Shkaff
Ну в целом да, если у вас какая-то Эрмитова мода высокого порядка, например, может быть удобнее квадратное зеркало. Только особо никто же не использует высшие моды.
Ну это всегда так, конечно. Любая неровность будет рассеивать свет в моды высоких порядков или вообще из резонатора.
Не очень понял точно про «циллиндр».
Victor_koly
Это я считаю, что правильно нашел когда-то соотношение того, при каком условие будет мало мод высоких порядков. Или вообще совсем других мод, например таких, которые возникают в полностью закрытом металлическими стенками микроволновом резонаторе. В таких резонаторах почти не шарю, но в той книге вводилось утверждение, что если в оптическом резонаторе сделать кроме 2 «оснований» резонатора ещё лишние отражающие стенки — выйдет очень много мод оптического диапазона (длина волны много меньше радиуса зеркала r) и с селективностью выйдут проблемы.
Радиус цилиндра — это такой условный цилиндр бесконечной высоты, в который можно вписать оба зеркала.
В принципе, в упомянутый мною цилиндр «малого» радиуса могут быть вписаны и прямоугольные зеркала.
И ещё по поводу полировки и качества отражения зеркал. Кажется в той же весьма старой книге было написано, что понятие «край зеркала как величины отражающей способности» должно быть резким, чуть ли не падать до нуля на диапазоне (R, R + lambda/2). Хотя кажется был и другой вариант — модель с зеркалами, у которых отражающая способность падает по гауссиане. Но, формально говоря, у таких зеркал наступает такой радиус R, что между упомянутыми мною точками
r1 = R, r2 = R + lambda/2 отражающая способность упадет в e раз.
Про высшие моды. Вроде как неустойчивый резонатор может использовать вывод излучения через край зеркала, где зеркала имеют центры сферической поверхности с центром на внешней стороне оси резонатора.
Victor_koly
Ещё придумал предельный случай моего резонатора. Полусфера радиусом lambda (я в курсе, что нормальный микрорезонатор имеет толщину нечетное число полуволн, когда нужно в его центре иметь максимум амплитуды), её покрытие — 15-20 слоев lambda/4.
Только в случае оптических длин волн мы туда не сможем завести свет, а на радиодиапазон из серебра можно изготовить и подвести напряжение нужной частоты.