Доброго времени суток.
Последние несколько лет я посвятил исследованию и созданию различных алгоритмов пространственной обработки сигналов в адаптивных антенных решётках, и продолжаю заниматься этим в рамках своей работы в настоящее время. Здесь я хотел бы поделиться теми знаниями и фишками, которые открыл для себя. Надеюсь, что это будет полезно для людей начинающих изучать эту область обработки сигналов или же просто интересующихся.
Антенная решётка – это набор антенных элементов, некоторым образом размещённых в пространстве. Упрощённо структуру адаптивной антенной решётки, которую мы будем рассматривать, можно представить в следующем виде:
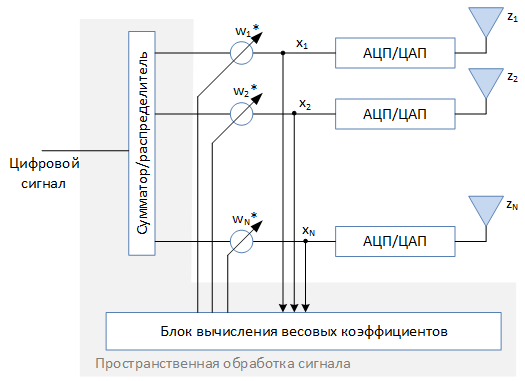
Адаптивные антенные решётки не редко называют «умными» антеннами (Smart antenna). «Умной» антенную решётку делает блок пространственной обработки сигнала и алгоритмы, реализованные в нём. Эти алгоритмы анализируют принимаемый сигнал и формируют набор весовых коэффициентов , которые определяют амплитуду и начальную фазу сигнала для каждого из элементов. Заданное амплитудно-фазовое распределение определяет диаграмму направленности всей решётки в целом. Возможность синтезировать диаграмму направленности необходимой формы и изменять её в процессе обработки сигнала — одна из главных особенностей адаптивных антенных решёток, позволяющая решать широкий спектр задач. Но обо всём по порядку.
Диаграмма направленности характеризует мощность сигнала, излучаемую в некотором направлении. Для простоты положим элементы решётки изотропными, т.е. для каждого из них мощность излучаемого сигнала не зависит от направления. Усиление или ослабление мощности, излучаемой решёткой в некотором направлении, получается вследствие интерференции ЭМВ, излученных различными элементами антенной решётки. Устойчивая интерференционная картина для ЭМВ возможна только при условии их когерентности, т.е. разность фаз сигналов не должна меняться со временем. В идеальном случае каждый из элементов антенной решётки должен излучать гармонический сигнал на одной и той же несущей частоте . Однако на практике приходится работать с узкополосными сигналами, имеющими спектр конечной ширины .
Пусть все элементы АР излучают один и тот же сигнал с комплексной амплитудой . Тогда на удаленном приёмнике принятый от n-ного элемента сигнал можно представить в аналитическом виде: где – задержка в распространении сигнала от антенного элемента до точки приёма.
Такой сигнал является «квазигармоническим», и для выполнения условия когерентности необходимо, чтобы максимальная задержка в распространении ЭМВ между любыми двумя элементами была много меньше характерного времени изменения огибающей сигнала , т.е. . Таким образом, условие на когерентность узкополосного сигнала можно записать следующим образом:
где — максимальное расстояние между элементами АР, а — скорость света.
При приёме сигнала когерентное суммирование производится в цифровом виде в блоке пространственной обработки. В этом случае комплексное значение цифрового сигнала на выходе этого блока определяется выражением:Последнее выражение удобнее представить в виде скалярного произведения N-мерных комплексных векторов в матричной форме:где w и x — векторы-столбцы, а — операция эрмитового сопряжения.
Векторное представление сигналов является одним из базовых при работе с антенными решётками, т.к. часто позволяет избежать громоздких математических выкладок. Кроме того, отождествление принятого в некоторый момент времени сигнала с вектором часто позволяет абстрагироваться от реальной физической системы и понять, что же именно происходит с точки зрения геометрии.
Чтобы рассчитать диаграмму направленности антенной решётки необходимо мысленно и последовательно «запустить» на неё набор плоских волн со всех возможных направлений. В этом случае значения элементов вектора x можно представить в следующем виде:где k – волновой вектор, и – азимутальный угол и угол места, характеризующие направление прихода плоской волны, – координата антенного элемента, – элемент фазирующего вектора s плоской волны с волновым вектором k (в англоязычной литературе фазирующий вектор называют steerage vector). Зависимость квадрата амплитуды величины y от и определяет диаграмму направленности антенной решётки на приём при заданном векторе весовых коэффициентов w.
Исследовать общие свойства диаграммы направленности антенных решёток удобно на линейной эквидистантной антенной решётке в горизонтально плоскости (т.е. ДН зависит только от азимутального угла ). Удобно с двух точек зрения: аналитических выкладок и визуального представления.
Рассчитаем ДН для единичного весового вектора (), следуя описанному выше подходу.
В итоге получим:
Полученная диаграмма направленности антенной решётки – периодическая функция от синуса угла. Это значит, что при определённых значениях соотношения d/? она имеет дифракционные (дополнительные) максимумы.
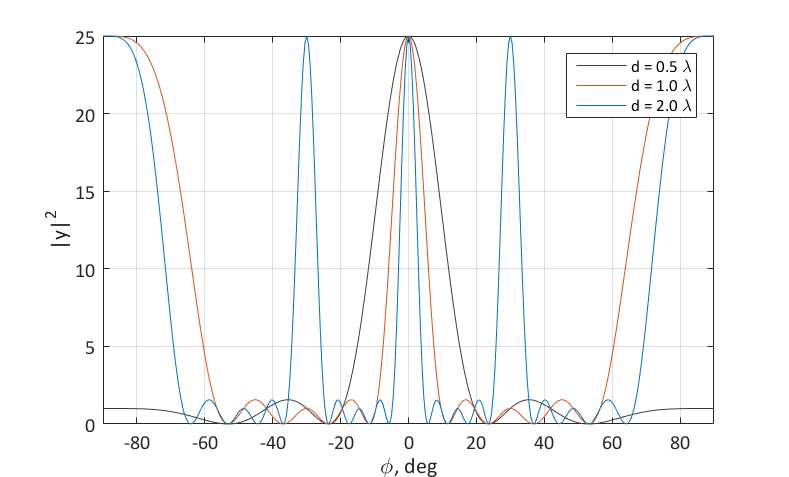 Ненормированная диаграмма направленности антенной решётки для N = 5
Ненормированная диаграмма направленности антенной решётки для N = 5
 Нормированная диаграмма направленности антенной решётки для N = 5 в полярной системе координат
Нормированная диаграмма направленности антенной решётки для N = 5 в полярной системе координат
Положение «дифракционников» можно посмотреть напрямую из формулы для ДН. Однако мы попробуем понять, откуда они берутся физически и геометрически (в N-мерном пространстве).
Элементы фазирующего вектора s представляют собой комплексные экспоненты , значения которых определяются величиной обобщённого угла . Если существуют два обобщённых угла, соответствующих различным направлениям прихода плоской волны, для которых выполняется , то это значит две вещи:
Связанные подобным образом направления прихода волны являются с точки зрения антенной решётки эквивалентными и не различимы между собой.
Как определить область углов, в которой всегда лежит только один главный максимум ДН? Сделаем это в окрестностях нулевого азимута из следующих соображений: величина набега фаз между двумя соседними элементами должна лежать в интервале от до .
Разрешая данное неравенство получим условие на область однозначности в окрестности нуля:
Видно, что размер области однозначности по углу зависит от соотношения d/?. Если d = 0.5?, то каждое направление прихода сигнала «индивидуально», а область однозначности охватывает полный диапазон углов. Если же d = 2.0?, то направления 0, ±30, ±90 – эквивалентны. На диаграмме направленности появляются дифракционные лепестки.
Обычно, дифракционные лепестки стремятся подавить с помощью направленных антенных элементов. В этом случае полная диаграмма направленности антенной решётки является произведением ДН одного элемента и решётки изотропных элементов. Параметры ДН одного элемента обычно выбирают исходя из условия на область однозначности антенной решётки.
Широко известна инженерная формула для оценки ширины главного лепестка антенной системы: , где D – характерный размер антенны. Формула используется для различного вида антенн, в том числе зеркальных. Покажем, что она справедлива и для антенных решёток.
Определим ширину главного лепестка первыми нулями ДН в окрестности главного максимума. Числитель выражения для обращается в ноль при . Первые нули соответствуют m = ±1. Полагая получаем .
Обычно ширину ДН направленности АР определяют по уровню половинной мощности (-3 дБ). В этом случае используют выражение:
Шириной главного лепестка можно управлять, задавая различные значения амплитуд для весовых коэффициентов антенной решётки. Рассмотрим три распределения:
На рисунке показаны получившиеся нормированные диаграммы направленности в логарифмическом масштабе: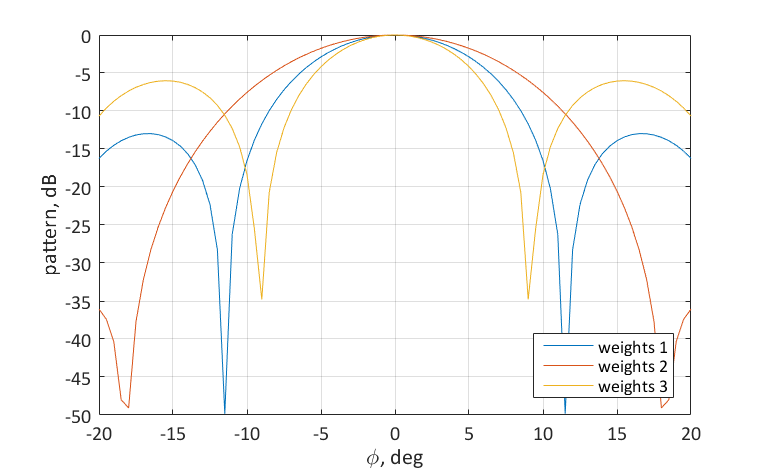
Из рисунка можно проследить следующие тенденции: спадающее к краям решётки распределение амплитуд весовых коэффициентов приводит к уширению главного лепестка ДН, но уменьшению уровня боковых лепестков. Увеличивающиеся к краям антенной решётки значения амплитуд, напротив, приводят к сужению главного лепестка и увеличению уровня боковиков. Здесь удобно рассмотреть предельные случаи:
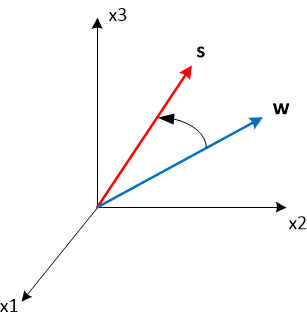
Итак, мы посмотрели, как можно регулировать ширину главного лепестка ДН АР. Теперь посмотрим, как порулить направлением. Вспомним векторное выражение для принятного сигнала. Пусть мы хотим, что бы максимум диаграммы направленности смотрел в некотором направлении . Это значит, что с этого направления должна приниматься максимальная мощность. Данному направлению соответствует фазирующий вектор в N-мерном векторном пространстве, а принимаемая мощность определяется как квадрат скалярного произведения этого фазирующего вектора на вектор весовых коэффициентов w. Скалярное произведение двух векторов максимально, когда они коллинеарны, т.е. , где ? – некоторый нормирующий множитель. Таким образом, если мы выберем весовой вектор равным фазирующему для требуемого направления, то повернём максимум диаграммы направленности.
Рассмотрим в качестве примера следующие весовые коэффициенты:
В итоге получим диаграмму направленности с главным максимумом в направлении 10°.
Теперь применим те же самые весовые коэффициенты, но не для приёма сигнала, а для передачи. Здесь стоит учесть, что при передаче сигнала направление волнового вектора меняется на противоположное. Это значит, что элементы фазирующего вектора для приёма и передачи отличаются знаком в показателе экспоненты, т.е. связаны между собой комплексным сопряжением. В итоге получим максимум диаграммы направленности на передачу в направлении -10°, что не совпадает с максимумом ДН на приём при тех же весовых коэффициентах.Что бы исправить ситуацию, необходимо применить комплексное сопряжение также и к весовым коэффициентам.
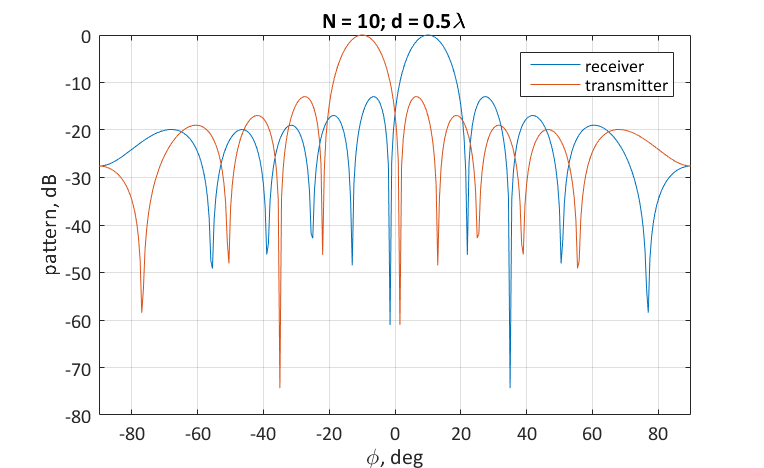
Описанную особенность формирования ДН на приём и передачу следует всегда иметь в виду при работе с антенными решётками.
Поставим задачку сформировать два главных максимума диаграммы направленности в направлении: -5° и 10°. Для этого выберем в качестве весового вектора взвешенную сумму фазирующих векторов для соответствующих направлений.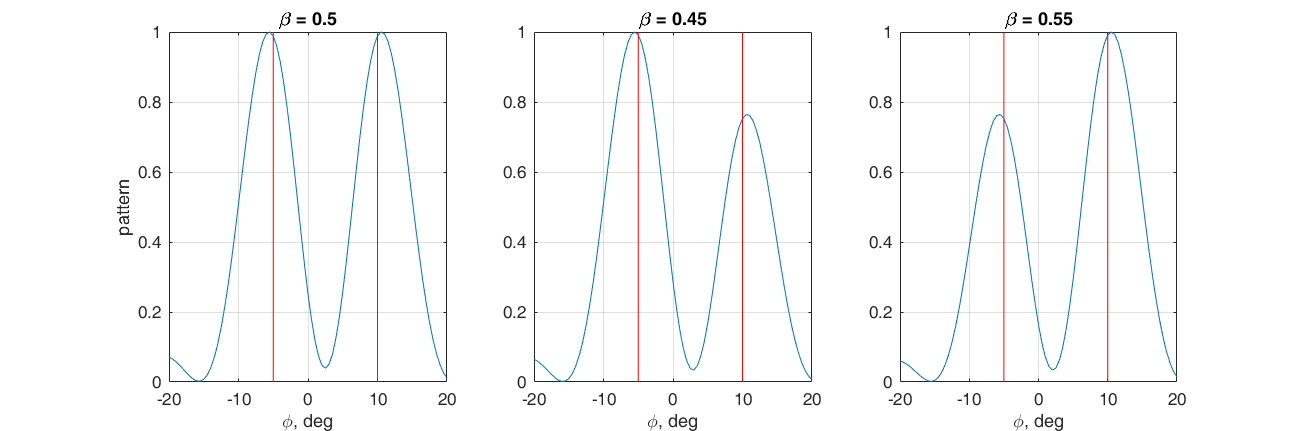 Регулируя коэффициент ? можно регулировать соотношение между главными лепестками. Здесь опять удобно посмотреть на происходящее в векторном пространстве. Если ? больше 0.5, то вектор весовых коэффициентов лежит ближе к s(10°), иначе к s(-5°). Чем ближе весовой вектор к одному из фазоров, тем больше соответствующее скалярное произведение, а следовательно и величина соответствующего максимума ДН.
Регулируя коэффициент ? можно регулировать соотношение между главными лепестками. Здесь опять удобно посмотреть на происходящее в векторном пространстве. Если ? больше 0.5, то вектор весовых коэффициентов лежит ближе к s(10°), иначе к s(-5°). Чем ближе весовой вектор к одному из фазоров, тем больше соответствующее скалярное произведение, а следовательно и величина соответствующего максимума ДН.
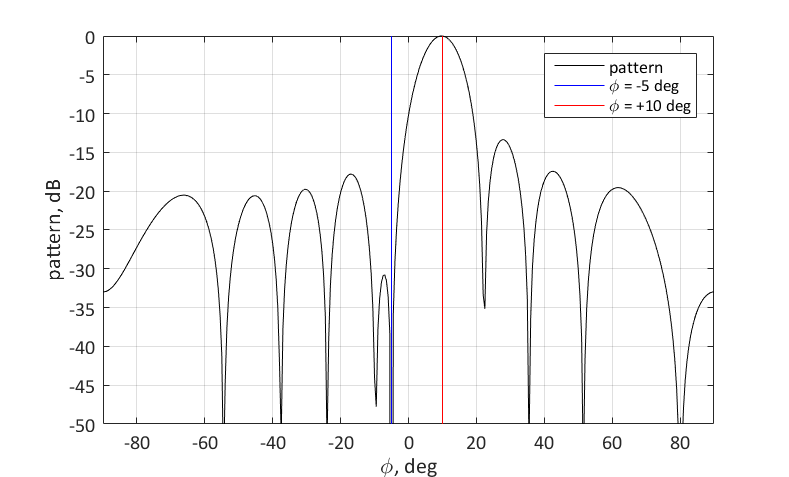
Однако стоит учесть, что оба главных лепестка имеют конечную ширину, и если мы захотим настроиться на два близких направления, то эти лепестки сольются в один, ориентированный на некоторое среднее направление.
Теперь попробуем настроить максимум диаграммы направленности на направление и одновременно подавить сигнал, приходящей с направления . Для этого необходимо выставить ноль ДН для соответствующего угла. Сделать это можно следующим образом:
где , а .
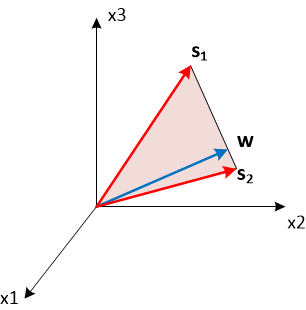
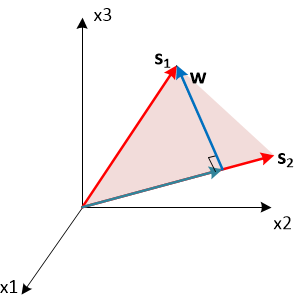
Геометрический смысл выбора весового вектора следующий. Мы хотим, что бы этот вектор w имел максимальную проекцию на и при этом был ортогонален вектору . Вектор можно представить в виде двух слагаемых: вектора коллинеарного и вектор ортогонального . Чтобы удовлетворить постановке задачи, необходимо выбрать вторую компоненту в качестве вектора весовых коэффициентов w. Рассчитать коллинеарную компоненту можно спроектировав вектор на нормированный вектор с помощью скалярного произведения.Соответственно, вычитая из исходного фазирующего вектора его коллинеарную компоненту, получим искомый весовой вектор.
Спасибо за внимание
Последние несколько лет я посвятил исследованию и созданию различных алгоритмов пространственной обработки сигналов в адаптивных антенных решётках, и продолжаю заниматься этим в рамках своей работы в настоящее время. Здесь я хотел бы поделиться теми знаниями и фишками, которые открыл для себя. Надеюсь, что это будет полезно для людей начинающих изучать эту область обработки сигналов или же просто интересующихся.
Что такое адаптивная антенная решётка?
Антенная решётка – это набор антенных элементов, некоторым образом размещённых в пространстве. Упрощённо структуру адаптивной антенной решётки, которую мы будем рассматривать, можно представить в следующем виде:

Адаптивные антенные решётки не редко называют «умными» антеннами (Smart antenna). «Умной» антенную решётку делает блок пространственной обработки сигнала и алгоритмы, реализованные в нём. Эти алгоритмы анализируют принимаемый сигнал и формируют набор весовых коэффициентов , которые определяют амплитуду и начальную фазу сигнала для каждого из элементов. Заданное амплитудно-фазовое распределение определяет диаграмму направленности всей решётки в целом. Возможность синтезировать диаграмму направленности необходимой формы и изменять её в процессе обработки сигнала — одна из главных особенностей адаптивных антенных решёток, позволяющая решать широкий спектр задач. Но обо всём по порядку.
Как формируется диаграмма направленности?
Диаграмма направленности характеризует мощность сигнала, излучаемую в некотором направлении. Для простоты положим элементы решётки изотропными, т.е. для каждого из них мощность излучаемого сигнала не зависит от направления. Усиление или ослабление мощности, излучаемой решёткой в некотором направлении, получается вследствие интерференции ЭМВ, излученных различными элементами антенной решётки. Устойчивая интерференционная картина для ЭМВ возможна только при условии их когерентности, т.е. разность фаз сигналов не должна меняться со временем. В идеальном случае каждый из элементов антенной решётки должен излучать гармонический сигнал на одной и той же несущей частоте . Однако на практике приходится работать с узкополосными сигналами, имеющими спектр конечной ширины .
Пусть все элементы АР излучают один и тот же сигнал с комплексной амплитудой . Тогда на удаленном приёмнике принятый от n-ного элемента сигнал можно представить в аналитическом виде: где – задержка в распространении сигнала от антенного элемента до точки приёма.
Такой сигнал является «квазигармоническим», и для выполнения условия когерентности необходимо, чтобы максимальная задержка в распространении ЭМВ между любыми двумя элементами была много меньше характерного времени изменения огибающей сигнала , т.е. . Таким образом, условие на когерентность узкополосного сигнала можно записать следующим образом:
где — максимальное расстояние между элементами АР, а — скорость света.
При приёме сигнала когерентное суммирование производится в цифровом виде в блоке пространственной обработки. В этом случае комплексное значение цифрового сигнала на выходе этого блока определяется выражением:Последнее выражение удобнее представить в виде скалярного произведения N-мерных комплексных векторов в матричной форме:где w и x — векторы-столбцы, а — операция эрмитового сопряжения.
Векторное представление сигналов является одним из базовых при работе с антенными решётками, т.к. часто позволяет избежать громоздких математических выкладок. Кроме того, отождествление принятого в некоторый момент времени сигнала с вектором часто позволяет абстрагироваться от реальной физической системы и понять, что же именно происходит с точки зрения геометрии.
Чтобы рассчитать диаграмму направленности антенной решётки необходимо мысленно и последовательно «запустить» на неё набор плоских волн со всех возможных направлений. В этом случае значения элементов вектора x можно представить в следующем виде:где k – волновой вектор, и – азимутальный угол и угол места, характеризующие направление прихода плоской волны, – координата антенного элемента, – элемент фазирующего вектора s плоской волны с волновым вектором k (в англоязычной литературе фазирующий вектор называют steerage vector). Зависимость квадрата амплитуды величины y от и определяет диаграмму направленности антенной решётки на приём при заданном векторе весовых коэффициентов w.
Особенности диаграммы направленности антенной решётки
Исследовать общие свойства диаграммы направленности антенных решёток удобно на линейной эквидистантной антенной решётке в горизонтально плоскости (т.е. ДН зависит только от азимутального угла ). Удобно с двух точек зрения: аналитических выкладок и визуального представления.
Рассчитаем ДН для единичного весового вектора (), следуя описанному выше подходу.
Математика тут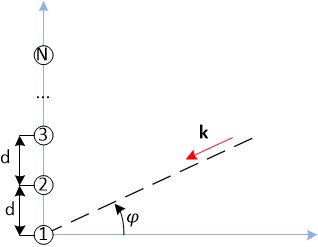
Проекция волнового вектора на вертикальную ось:
Вертикальная координата антенного элемента с индексом n:
Здесь d – период антенной решётки (расстояние между соседними элементами), ? — длина волны. Все иные элементы вектора r равны нулю.
Принимаемый антенной решёткой сигнал записывается в следующем виде:Применим формулу для суммы геометрической прогрессии и представление тригонометрических функций через комплексные экспоненты :

Проекция волнового вектора на вертикальную ось:
Вертикальная координата антенного элемента с индексом n:
Здесь d – период антенной решётки (расстояние между соседними элементами), ? — длина волны. Все иные элементы вектора r равны нулю.
Принимаемый антенной решёткой сигнал записывается в следующем виде:Применим формулу для суммы геометрической прогрессии и представление тригонометрических функций через комплексные экспоненты :
В итоге получим:
Периодичность диаграммы направленности
Полученная диаграмма направленности антенной решётки – периодическая функция от синуса угла. Это значит, что при определённых значениях соотношения d/? она имеет дифракционные (дополнительные) максимумы.


Положение «дифракционников» можно посмотреть напрямую из формулы для ДН. Однако мы попробуем понять, откуда они берутся физически и геометрически (в N-мерном пространстве).
Элементы фазирующего вектора s представляют собой комплексные экспоненты , значения которых определяются величиной обобщённого угла . Если существуют два обобщённых угла, соответствующих различным направлениям прихода плоской волны, для которых выполняется , то это значит две вещи:
- Физически: плоские волновые фронты, приходящие с этих направлений, индуцируют на элементах антенной решётки идентичные амплитудно-фазовые распределения электромагнитных колебаний.
- Геометрически: фазирующие вектора для этих двух направлений совпадают.
Связанные подобным образом направления прихода волны являются с точки зрения антенной решётки эквивалентными и не различимы между собой.
Как определить область углов, в которой всегда лежит только один главный максимум ДН? Сделаем это в окрестностях нулевого азимута из следующих соображений: величина набега фаз между двумя соседними элементами должна лежать в интервале от до .
Разрешая данное неравенство получим условие на область однозначности в окрестности нуля:
Видно, что размер области однозначности по углу зависит от соотношения d/?. Если d = 0.5?, то каждое направление прихода сигнала «индивидуально», а область однозначности охватывает полный диапазон углов. Если же d = 2.0?, то направления 0, ±30, ±90 – эквивалентны. На диаграмме направленности появляются дифракционные лепестки.
Обычно, дифракционные лепестки стремятся подавить с помощью направленных антенных элементов. В этом случае полная диаграмма направленности антенной решётки является произведением ДН одного элемента и решётки изотропных элементов. Параметры ДН одного элемента обычно выбирают исходя из условия на область однозначности антенной решётки.
Ширина главного лепестка
Широко известна инженерная формула для оценки ширины главного лепестка антенной системы: , где D – характерный размер антенны. Формула используется для различного вида антенн, в том числе зеркальных. Покажем, что она справедлива и для антенных решёток.
Определим ширину главного лепестка первыми нулями ДН в окрестности главного максимума. Числитель выражения для обращается в ноль при . Первые нули соответствуют m = ±1. Полагая получаем .
Обычно ширину ДН направленности АР определяют по уровню половинной мощности (-3 дБ). В этом случае используют выражение:
Пример

Шириной главного лепестка можно управлять, задавая различные значения амплитуд для весовых коэффициентов антенной решётки. Рассмотрим три распределения:
- Равномерное распределение амплитуды (weights 1): .
- Спадающее к краям решётки значения амплитуды (weights 2):
- Увеличивающиеся к краям решётки значения амплитуды(weights 3):
На рисунке показаны получившиеся нормированные диаграммы направленности в логарифмическом масштабе:

Из рисунка можно проследить следующие тенденции: спадающее к краям решётки распределение амплитуд весовых коэффициентов приводит к уширению главного лепестка ДН, но уменьшению уровня боковых лепестков. Увеличивающиеся к краям антенной решётки значения амплитуд, напротив, приводят к сужению главного лепестка и увеличению уровня боковиков. Здесь удобно рассмотреть предельные случаи:
- Амплитуды весовых коэффициентов всех элементов, кроме крайних, равны нулю. Веса для крайних элементов равны единице. В этом случае решётка становится эквивалентна двухэлементной АР с периодом D = (N-1)d. Не трудно прикинуть по представленной выше формуле ширину главного лепестка. При этом боковики превратятся в дифракционные максимумы и выровнятся по уровню с главным максимумом.
- Вес центрального элемента равен единице, а всех остальных – нулю. В этом случае мы получили по сути одну антенну с изотропной диаграммой направленности.
Направление главного максимума
Итак, мы посмотрели, как можно регулировать ширину главного лепестка ДН АР. Теперь посмотрим, как порулить направлением. Вспомним векторное выражение для принятного сигнала. Пусть мы хотим, что бы максимум диаграммы направленности смотрел в некотором направлении . Это значит, что с этого направления должна приниматься максимальная мощность. Данному направлению соответствует фазирующий вектор в N-мерном векторном пространстве, а принимаемая мощность определяется как квадрат скалярного произведения этого фазирующего вектора на вектор весовых коэффициентов w. Скалярное произведение двух векторов максимально, когда они коллинеарны, т.е. , где ? – некоторый нормирующий множитель. Таким образом, если мы выберем весовой вектор равным фазирующему для требуемого направления, то повернём максимум диаграммы направленности.

Рассмотрим в качестве примера следующие весовые коэффициенты:
В итоге получим диаграмму направленности с главным максимумом в направлении 10°.
Теперь применим те же самые весовые коэффициенты, но не для приёма сигнала, а для передачи. Здесь стоит учесть, что при передаче сигнала направление волнового вектора меняется на противоположное. Это значит, что элементы фазирующего вектора для приёма и передачи отличаются знаком в показателе экспоненты, т.е. связаны между собой комплексным сопряжением. В итоге получим максимум диаграммы направленности на передачу в направлении -10°, что не совпадает с максимумом ДН на приём при тех же весовых коэффициентах.Что бы исправить ситуацию, необходимо применить комплексное сопряжение также и к весовым коэффициентам.

Описанную особенность формирования ДН на приём и передачу следует всегда иметь в виду при работе с антенными решётками.
Поиграем с диаграммой направленности
Несколько максимумов
Поставим задачку сформировать два главных максимума диаграммы направленности в направлении: -5° и 10°. Для этого выберем в качестве весового вектора взвешенную сумму фазирующих векторов для соответствующих направлений.
 Регулируя коэффициент ? можно регулировать соотношение между главными лепестками. Здесь опять удобно посмотреть на происходящее в векторном пространстве. Если ? больше 0.5, то вектор весовых коэффициентов лежит ближе к s(10°), иначе к s(-5°). Чем ближе весовой вектор к одному из фазоров, тем больше соответствующее скалярное произведение, а следовательно и величина соответствующего максимума ДН.
Регулируя коэффициент ? можно регулировать соотношение между главными лепестками. Здесь опять удобно посмотреть на происходящее в векторном пространстве. Если ? больше 0.5, то вектор весовых коэффициентов лежит ближе к s(10°), иначе к s(-5°). Чем ближе весовой вектор к одному из фазоров, тем больше соответствующее скалярное произведение, а следовательно и величина соответствующего максимума ДН.
Однако стоит учесть, что оба главных лепестка имеют конечную ширину, и если мы захотим настроиться на два близких направления, то эти лепестки сольются в один, ориентированный на некоторое среднее направление.
Один максимум и ноль
Теперь попробуем настроить максимум диаграммы направленности на направление и одновременно подавить сигнал, приходящей с направления . Для этого необходимо выставить ноль ДН для соответствующего угла. Сделать это можно следующим образом:
где , а .

Геометрический смысл выбора весового вектора следующий. Мы хотим, что бы этот вектор w имел максимальную проекцию на и при этом был ортогонален вектору . Вектор можно представить в виде двух слагаемых: вектора коллинеарного и вектор ортогонального . Чтобы удовлетворить постановке задачи, необходимо выбрать вторую компоненту в качестве вектора весовых коэффициентов w. Рассчитать коллинеарную компоненту можно спроектировав вектор на нормированный вектор с помощью скалярного произведения.Соответственно, вычитая из исходного фазирующего вектора его коллинеарную компоненту, получим искомый весовой вектор.

Некоторые дополнительные замечания
- Везде выше я опустил вопрос нормировки весового вектора, т.е. его длины. Так вот, нормировка весового вектора не влияет на характеристики диаграммы направленности антенной решётки: направление главного максима, ширину главного лепестка и т.п. Можно также показать, что эта нормировка не влияет и на ОСШ на выходе блока пространственной обработки. В связи с этим при рассмотрении алгоритмов пространственной обработки сигнала обычно принимаю единичную нормировку весового вектора, т.е.
- Возможности по формированию ДН антенной решётки определяются количеством элементов N. Чем больше элементов, тем шире возможности. Тем больше степеней свободы при осуществлении пространственной весовой обработки, больше вариантов как «покрутить» весовым вектором в N-мерном пространстве.
- При осуществлении приёма ДН антенной решётки физически не существует, а все это существует лишь в «воображении» вычислительного блока, осуществляющего обработку сигнала. Это значит, что в один и тот же момент времени можно синтезировать несколько ДН и вести независимо обработку сигналов приходящих с различных направлений. В случае с передачей все несколько сложнее, однако также существует возможность синтезировать несколько ДН для передачи различных потоков данных. Такая технология в системах связи получила название MIMO.
- С помощью представленного matlab кода можно самостоятельно поиграться с ДН
Код% antenna array settings N = 10; % number of elements d = 0.5; % period of antenna array wLength = 1; % wavelength mode = 'receiver'; % receiver or transmitter % weights of antenna array w = ones(N,1); % w = 0.5 + 0.3*cos(2*pi*((0:N-1)-0.5*(N-1))/N).'; % w = 0.5 - 0.3*cos(2*pi*((0:N-1)-0.5*(N-1))/N).'; % w = exp(2i*pi*d/wLength*sin(10/180*pi)*(0:N-1)).'; % b = 0.5; w = b*exp(2i*pi*d/wLength*sin(+10/180*pi)*(0:N-1)).' + (1-b)*exp(2i*pi*d/wLength*sin(-5/180*pi)*(0:N-1)).'; % b = 0.5; w = b*exp(2i*pi*d/wLength*sin(+3/180*pi)*(0:N-1)).' + (1-b)*exp(2i*pi*d/wLength*sin(-3/180*pi)*(0:N-1)).'; % s1 = exp(2i*pi*d/wLength*sin(10/180*pi)*(0:N-1)).'; % s2 = exp(2i*pi*d/wLength*sin(-5/180*pi)*(0:N-1)).'; % w = s1 - (1/N)*s2*s2'*s1; % w = s1; % normalize weights w = w./sqrt(sum(abs(w).^2)); % set of angle values to calculate pattern angGrid_deg = (-90:0.5:90); % convert degree to radian angGrid = angGrid_deg * pi / 180; % calculate set of steerage vectors for angle grid switch (mode) case 'receiver' s = exp(2i*pi*d/wLength*bsxfun(@times,(0:N-1)',sin(angGrid))); case 'transmitter' s = exp(-2i*pi*d/wLength*bsxfun(@times,(0:N-1)',sin(angGrid))); end % calculate pattern y = (abs(w'*s)).^2; %linear scale plot(angGrid_deg,y/max(y)); grid on; xlim([-90 90]); % log scale % plot(angGrid_deg,10*log10(y/max(y))); % grid on; % xlim([-90 90]);
Какие задачи можно решать с помощью адаптивной антенной решётки?
Оптимальный приём неизвестного сигнала
Если направление приход сигнала неизвестно (а если канал связи многолучевой, направлений вообще несколько), то проанализировав принимаемый антенной решёткой сигнал, можно сформировать оптимальный весовой вектор w так, что ОСШ на выходе блока пространственной обработки будет максимальным.
Оптимальный приём сигнала на фоне помех
Здесь задача ставится следующим образом: пространственные параметры ожидаемого полезного сигнала известны, однако во внешней среде существуют источники помех. Необходимо максимизировать ОСШП на выходе АР, максимально понизив влияние помех на приём сигнала.
Оптимальная переда сигнала пользователю
Данная задача решается в системах мобильной связи (4G, 5G), а также в Wi-Fi. Смысл прост: c помощью специальных пилотных сигналов в канале обратной связи пользователя производится оценка пространственных характеристик канала связи, и на её основе выбирается оптимальный для передачи вектор весовых коэффициентов.
Пространственное мультиплексирование потоков данных
Адаптивные антенные решётки позволяют вести передачу данных нескольким пользователям в одно и то же время на одной и той же частоте, сформировав для каждого из них индивидуальную ДН. Данная технология называется MU-MIMO и в настоящее время активно внедряется (а где-то уже) в системы связи. Возможность пространственного мультиплексирования предусмотрена, например, в стандарте мобильной связи 4G LTE, Wi-Fi стандарте IEEE802.11ay, стандартах мобильной связи 5G.
Виртуальные антенные массивы для радаров
Цифровые антенные решётки позволяют с помощью нескольких передащих антенных элементов сформировать для обработки сигнала виртуальную антенную решётку существенно больших размеров. Виртуальная решётка имеет все характеристики реальной, однако для своей реализации требует меньших аппаратных затрат.
Оценка параметров источников излучения
Адаптивные антенные решётки позволяют решать задачу оценки числа, мощности, угловых координат источников радиоизлучения, устанавливать статистическую связь между сигналами различных источников. Главным достоинством адаптивных антенных решёток в этом вопросе является способность к сверхразрешению близкорасположенных источников излучения. Источников, угловое расстояние между которыми меньше ширины главного лепестка диаграммы направленности антенной решётки (предел разрешения Релея). Главным образом это становится возможным за счёт векторного представления сигнала, известной сигнальной модели, а также аппарата линейной математики.
Спасибо за внимание


Astroscope
У меня дилетантский вопрос. Как практически осуществляется фазирование в, скажем, дециметровом диапазоне?
Psychosynthesis
Вопрос именно про фазирование или про адаптивность?
Если вас строго фазирование интересует, то, как вариант, например, длинной волновода до каждого элемента решётки.
Astroscope
Про адаптивность. Чисто практический вопрос, как (в смысле насколько сложно) сделать небольшой стек и управлять диаграммой направленности электрически, а не традиционно поворачивая антенну механическим поворотным устройством? Когда в стеке буквально несколько излучателей (собственно, от двух), то задачу решают в лоб, коммутируя линии с каким-то приемлемым шагом, чтобы изменением их длины изменять фазу на каждом элементе. Этот методе едва ли практически возможен в стеке уже с тремя-четырьмя рядами в трех-четырех этажах — одновременно увеличивается и количество коммутируемых линий, и потребная точность изменения их длины, поскольку с ростом числа элементов сужается достижимая диаграмма направленности. Про радары сантиметровых диапазонов вообще молчу.
Psychosynthesis
Когда излучателей много, используют электрические фазовращатели.
Но, опять же, что касается чисто практических вопросов — от механического сканирования отказываются очень редко, разве что в больших стационарных РЛС.
Из всех бортовых РЛС с ФАР, которые мне довелось видеть всего пара не имели механического привода. Банально потому, что при разумных габаритах электрическим сканированием достаточную ширину обзора не получить.
DryominG
Существуют различные техники фазирования (ака фазовращатели):
1) Линии задержки на распределённых элементах (отрезки фидерной линии, волновода, микрополосковой линии);
2) Сосредоточенные реактивные элементы (НЧ/ВЧ фильтры на конденсаторах/катушках);
3) Квадратурные ответвители с реактивной управляемой нагрузкой (варакторы, например);
4) И др.
В дециметровом диапазоне длина волны очень велика, поэтому линии задержки и квадратурные ответвители непрактичны.
Psychosynthesis
Во всём согласен, кроме п.2
На реактивных элементах обычно заметные потери, поэтому именно «на практике» такие конструкции встречаются достаточно редко. Разве что у радиолюбителей, в виде каких-нибудь балунов, но там это чаще несколько задач решает, например согласование.
Astroscope
Пожалуйста ткните носом в какие-то практические конструкции в районе дециметрового диапазона. Я не издеваюсь, а прошу о помощи. :)
a_zin
DryominG
Самое интересное, конечно же, это конструкция ответвителя и элементов L6-L7. Есть подробности об этих элеменьах схемы?
a_zin
evmt
Не уверен насчет применения в наши дни ФАР дециметрового диапазона волн, разве что малоэлементные какие-то. Обычно это все таки устройства СВЧ или КВЧ.
В цифровых антенных решетках сигналы синтезируются в цифровом виде уже с необходимыми сдвигами фаз и амплитудными весовыми коэффициентами для каждого элемента. В аналоговых ФАР используются управляемые фазовращатели, либо полупроводниковые (обычно на pin-диодах), либо ферритовые.
Astroscope
Я радиолюбитель. Мне интересно узнать, как это устроено на практике и, если подъемно, попробовать повторить. Например, мне интересна антенна для связи с LEO спутниками. Для этого уже достаточно «усиления» порядка, скажем, 6dBd. Больше — весьма лучше, но увеличиваются требования к точности наведения антенны на движущийся спутник. Заманчиво положить на крышу стек и вращать диаграмму электрически, вместо вращать механическим поворотным устройством традиционную антенну. Естественно, речь не о сотнях или тысячах элементов в решетке радара, а о девяти-шестнадцати в лучшем случае.
DryominG
Существуют готовые фазовращатели, можно это превратить в минипроект, но выйдет в копеечку:
https://www.minicircuits.com/WebStore/PhaseShifters.html
Но для начала нужно определить целесообразность решения с электронным сканированием: определить необходимые углы сканирования, диаграмму направленности единичной антенны, рассчитать Array Factor и решить готовы ли Вы мириться с затуханием усиления решётки антенн на максимальных углах сканирования. Думаю механическое сканирование будет намного дешевле в реализации и не менее интересно.
zbot
несколько излучателей на каждый из которых приходит сигнал сдвинутый по фазе, для этого ставим управляемые линии задержки для каждого излучателя.
ZEvS_Poisk
Ну, например, установкой квадратурного модулятора в тракте каждого антенного элемента. С помощью КМ, можно вращать фазу на все 360 градусов, а еще и амплитудой управлять. Это если передатчик, а если антенная система работает на прием, то тоже самое ставится в систему первого преобразования, между смесителями и гетеродином, потом первые ПЧ объединяются.
Автору, большое спасибо, очень интересная статья!
rroyter
Вам надо в SpaceX, там как раз сейчас разрабатывают компактные фазированные решётки для StarLink'а.
shalm
Лучше пусть здесь продолжает, плавно переходя к железу, потому что вопрос, как это сделать дома может стать вполне актуальным довольно скоро
Psychosynthesis
Вообще здоровская статья, ощущение, словно я только что побывал на какой-то из пар своего пятого курса, которую когда-то проспал и пришлось теперь изучать подробнее =)
nuearth
Статья отличная. Тоже ощутил себя на паре какого-нибудь УГФС!


Чтобы статья зашла, думаю нужно её несколько раз неспешно прочесть и осмыслить.
Не знаю, можно ли как-то проще объяснять такие трудные штуки?
Технология адаптивных антенных решеток это явно технология будущего.
Думаю, автор видел практическую реализацию от дочки Facebook — terragraph.
Устройства связи для городской застройки на 802.11ad и 802.11ay с антенными массивами 2x288 элементов!
В их технических данных можно увидеть значение 35дБ усиления!
Это вам не 3дБ выигрыша от ClientLink и подобных технологий.
Вот ссылка на fccid.io чтобы глянуть что же там внутри.
У меня есть вопрос к автору статьи.
На каких частотах адекватно возможно создание антенных решеток, чтобы они:
1. умещались в корпус мобильного устройства?
2. умещались в корпус стандартной точки доступа, размером, скажем, 15x15 см?
В 11ax точках доступа до 8 приёмо-передачтиков, но в мобильных устройствах такого не ожидается. Вот на 60ГГц уже наверняка можно больше элементов размещать…
DryominG
Позволю себе ответить/добавить.
1) Зависит от технологии. 60 ГГц (V-band) это граничный диапазон для технологии PCB. Т.е. геометрические размеры микрополосковых линий, переходов между слоями плат, СВЧ элементов уже упираются в границу возможностей тенологии PCB. Из собственного опыта, двуполяризационная антенная решётка 2x2 из дипольных излучающих элементов упёрлась в дозволенные технологические возможности.
Использование же литографии избавит от таких проблем, но это уже упирается в совсем иной ценовой диапазон. 60 ГГц это 5 мм длины волны, а с учётом диэлектрической проницаемости PCB, размер одной ячейки АФАР выходит примерно 1 мм.
2) Однополяризационная АФАР на 60 ГГц на плате 15х15 см вместит достаточно элементов, чтобы запутаться в разводке запитывающей сети, т.е. 140х140 элементов можно разместить. Задачу обычно ставят на основе (1) частоты, (2) количества элементов для требуемых параметров формируемого луча.
DegZ Автор
Мне очень помогли векторные аналогии, ими я и постарался оперировать при повествовании.
Характерный размер решётки D = Nd, где обычно период d порядка длины волны ? (0.5 — 1.5). Располагать элементы ближе не имеет смысла по двум причинам:
1. Габариты и взаимное ЭМ влияние.
2. Получается маленькая апертура (широкий луч) и высокая пространственная корреляция сигнала в элементах (если говорить о борьбе с замираниями).
Итого получаем, для 2.4 ГГц (? = 12.5 см) две антенны вдоль одной размерности, для 60ГГц (? = 5 мм) — около 40-60 штук. Если позволяют габариты антенных элементов, то число антенн можно удвоить за счёт добавления элементов с ортогональной поляризацией.
DryominG
Позвольте поправить Вас. На практике антенны на 60 ГГц, да и на 2.4 ГГц, не делают навесными в воздухе, т.е. без подложки. Это вносит изменения в эффективную длинну антенн, уменьшая её. Тот же FR4 имеет относительную диэлектрическую проницаемость, которая уменьшает антенну примерно в 2 раза, увеличивая количество излучающих элементов вдвое, соответственно.
DegZ Автор
Спасибо за интересную информацию.
Уменьшаются габариты отдельного элемента, т.к. они завязаны на длину волны в диэлектрике. Таким образом, геометрически на единицу площади может поместиться больше элементов. При этом на характеристики решётки в целом влияет расстояние между элементами в единицах длины волны в свободном пространстве, а на него свойства подложки влиять не должны. Я не прав?
DryominG
Правы! По причине формирования луча именно в дальней зоне в расчёт идёт длина волны в свободном пространстве. Наличие физического ограничения в виде необходимости каким-либо образом распечатать\зафиксировать излучающие элементы на диэлектрической подложке: (1) уменьшает геометрию излучающего элемента, (2) позволяет уменьшить расстояние между излучающими элементами меньше половины длины волны в свободном пространстве, что избавляет от боковых лепестков, но и (3) вносит потери, (4) создаёт предпосылки для формирования бегущих волн в подложке (ака потери и взаимное влияние), (5) увеличивает взаимное влияние в ближней зоне.
cuwHuk
Я бы сказал, что MIMO это частный случай технологии разнесённого приёма/передачи.
DegZ Автор
В контексте цитаты подразумевалось SU-MIMO и MU-MIMO. В общем случае системы из нескольких антенн могут быть использованы не только для ведения направленной передачи, но, например, для изменения статистики замираний.
Thetree
Спасибо. Очень доступно. А как поведет себя ДН если решетка неравномерная и неэквидистантная? Например если решетка состоит из 5 элементов с расстояниями между парами соседних антенн определенными как 3,5,2,7 длинн волн. Не всегда есть возможность поставить антенны равномерно или упорядочено. Например если требуется снизить ширину ДН, а количество каналов/антенн сильно ограничено. Интуитивно вроде как должно работать. Что если соблюдать когеррентность только в пределах 360 градусов фазы несущего сигнала?
DegZ Автор
Чтобы получить ответ на этот вопрос проще всего численно рассчитать ДН, подставив в общую формулу для фазирующего вектора желаемые координаты элементов. Если же мы хотим примерно прикинуть вид ДН, то тут можно попробовать «разделить слона на бифштексы». Иными словами, выделить подсистемы, поведение которых нам понятно, а потом оценить их взаимное влияние друг на друга.
«Новая» решётка имеет область однозначности ±19.5 градусов и ширину главного максимума 3.4 градуса. Если главный максимум на нуле, то первые дифракционники будут лежать примерно на ±39 градусов (здесь есть ошибка из-за нелинейности sin на больших углах).
Теперь посмотрим, что из себя представляет «новый» элемент. Это пара антенн на расстоянии 0.5?. Ширина главного лепестка такого «нового элемента» около 50-60 градусов (можно прикинуть через ?/D).
В итоге получаем как миннимум три максимума диаграммы направленности различной высоты с шириной около 3.4 градуса. Разница высот дифракционников по сравнению с главным максимумом более 3 дБ, т.к. дифракционники выходят за границы главного лепестка направленного элемента). Это все верно, если весовые коэффициенты единичные. Теперь можно подвигать двумя вещами: направленностью решётки и направленностью её элемента. Поворачивая ДН антенного элемента (фазируя спарки) можно «переключать» дифракционники, т.е. манипулировать их высотой. Внутри главного лепестка направленного элемента положение главного луча можно подвигать задавая различные набеги фаз между «спарками».
nuearth
Я попробую задать вопрос, про частный случай, может он будет близок к теме, хотя может и весьма тривиален.
Сейчас в современных доступных топовых Wi-Fi точках доступа MIMO 4x4:3
Расстояние между двухдиапазонными антенными разниться от вендора к вендору.
Даже если брать схему 2x2:2 то расстояние также разнится.
Что я замерял было от 1,32 лямбда до 3,56 лямбда на частоте 5260 МГц.
Вопросы:
1. По каким критериям выбирается это расстояние?
2. Можно ли говорить про «оптимальное» расстояние или всё зависит от задачи?
DegZ Автор
Всё зависит от задачи.
В случае MIMO 2x2 расстояние между элементами не играет существенной роли, т.к. предполагается разнесение потоков данных по поляризации ЭМВ, а не по лучу в пространстве. Обычно антенны точки доступа находятся под углом 90 градусов друг к другу.
Если говорить про разнесённый приём/передачу на одной поляризации в многолучевом канале, то тут важным фактором является пространственная корреляция между антеннами. Грубо — если в одной антенне сигнал пропал (неудачно сложились лучи), то во второй антенне он должен остаться. В этом случае расстояние между элементами следует выбирать больше, чем радиус пространственной корреляции. Значение этой величины зависит от условий функционирования системы. По некоторым прикидкам для пользователя системы мобильной связи это значение меньше длины волны, а для базовой станции — несколько длин волн.
В случае радаров или однолучевого канала все значительно проще. Условие на расстояние между элементами определяется из двух соображений:
1. Область предполагаемого положения цели должна находиться в области однозначности АР.
2. Дифракционники, если они есть, должны давиться ДН элементов.
Идеальный случай — 0.5?. Но здесь ограничения на размеры элементов и волноводных трактов. Минимальное расстояние, что я встречал было 0.55?, хотя это не совсем честно. В решётке было 2 строки узконаправленных по углу места элементов с периодом 1.1?, сдвинутые друг относительно друга на 0.55?. В проекции на горизонтальную плоскость получалась линейная эквидистантная решётка с указанным периодом.
Thetree
Спасибо за пример и за матлаб код. Потестировал его с разными абсолютно неэквидистантными наборами сенсоров. Общее впечатление таково, что есть какой-то многомерный ресурс и когда мы вытягиваем из него один параметер (например сужаем главный лепесток ДН), то на другие параметры типа сектор однозначности, уровень боковых и т.п. ресурса уже не хватает. Тогда надо увеличивать ресурс, т.е. добавлять антенны и что-то уже может получиться.
Позвольте спросить о роли поляризации. Как а понимаю, в условиях многолучевого распортранения могут появиться сильные кросс-поляризационные компоненты которые могут сильно подпортить поляризационное разделение каналов. Какова эффективность поляризационного разделения? Что вы наблюдали на практике? Можно-ли сказать например что с вероятностью 90% вредный кросс компонент не превысит скажем 30% от основной поляризации?
DegZ Автор
При многолучевом распространении поляризация сигнала «вертится» довольно сильно, особенно когда лучей много. Тут все завязано на свойства отражающих поверхностей и пути сигнала.
Я бы так не сказал. Разделение каналов они не подпортят, просто оно будет выполнено несколько иначе, чем одна антенна передаёт один поток данных, а вторая — другой.
tvant
1. Я не совсем понял упрощённую структурную схему антенной решётки (с подписью пространственная обработка сигнала). Неужели автор оцифровывает непосредственно тонкую структуру сигнала сразу с антенны? Без усиления-фильтрации, детектирования и выделения огибающих (амплитудных, фазовых и пр.)? Если это так, то какой АЦП использует автор (скорость дискретизации и разрядность) и каким практическим диапазоном радиоволн оперирует автор в реальных разработках? Я понимаю, что в теории для алгоритмической обработки границ нет, но автор говорит о практике.
2. На всех диаграммах направленности/чувствительности нормированных и нет, что в линейных, что в полярных координатах есть фишка. На 90 и 270 градусов лепесток чего-то (нет указания на величину, предположительно, амплитуда сигнала) шире главного/основного. Как автор этот феномен отсекает на практике? Иначе, вообще, работать с такой антенной невозможно, боковая или тыльная ЭМ засветка небольшой мощности задушит любой полезный сигнал с основного лепестка.
DegZ Автор
Добрый день.
Здесь Вы правы. Дифракционные лепестки в большинстве случаев это зло, и с ним нужно бороться.1. Вы правы. На рисунке отсутствует RF-часть. Сделано это преднамеренно, дабы не усложнять схему. Между антенной и АЦП/ЦАП безусловно должны присутствовать усилитель и полосовой фильтр. Если говорить про КВ диапазон, то можно цифровать сигнал без манипуляций с несущей частотой. Для более высоких диапазонов (например, 2.5 ГГц или 60 ГГц) подразумевается аналоговое преобразование несущей частоты перед оцифровкой сигнала.
2. Большая ширина лепестков на больших углах связана с нелинейностью преобразования обобщённого угла в реальный посредством sin(x). Представленные диаграммы построены для решёток с изотропными ДН. На практике используют направленные или слабо направленные элементы. Таким образом сигнал с крайних направлений «фильтруется» именно элементами АР.
tvant
1. Исключение RF-части из структурной схемы вводит начинающих в заблуждение, т.к. на высоких частотах (будем считать что выше 1 ГГц) управление фазой сигнала на передаче и адаптация фазы на приёме происходит в RF-части пусть и под внешним управлением. Думаю, автору нужно написать ещё статью про основы RF-преобразований и механизмы управления этими процессами. Тогда получится полный обзор про адаптивные решётки: сначала теория лежащая в основе, затем способы реализации теоретического задела.
2. Направленные элементы решётки превратят всю конструкцию в строго направленную антенну, любая адаптация по фазе только снизит излучаемую мощность по основному лепестку и мало что даст по отклонённому направлению. Весь кайф решётки именно в равномерной диаграмме направленности элементов по оси всей конструкции. Самый простой подходящий для решётки антенный элемент — это диполь (или любая его разновидность) с восьмёркой в диаграмме направленности (если в 3D то это: тор или тороид), при этом обратный лепесток глушат непроницаемым для выбранного диапазона экраном. Если это плоская система диполей, то визуально ДН можно представить как половинки теннисных шариков (слегка сдавленных по бокам) на шахматной доске. Если свернуть систему диполей в кольцо, то получим автомобильную покрышку обклеенную полушариками. Из этой визуализации понятен и принцип борьбы с боковухой на нужной частоте: используем экранирование по критичным направлениям (пассивные антенные элементы, рефлекторы и прочие RF заморочки).
helg1978
Спасибо, отличная статья!
Я когда-то занимался подобным — управлял массивом антенн, задача была сформировать минимумы в диаграмме для 2-3 источников помех (глушилок) что б по основному лепестку связь продолжала работать.
nuearth
Ко всем хорошо понимающим в теме вопрос: подскажите название годного учебника (или нескольких) на тему антенн. Можно на английском.
DryominG
Это конечно же Константин Баланис (Antenna Theory. C. Balanis).
Более теоретическая книга, если что-то нужно будет понять глубже, — это Роберт Коллин (Field theory of guided waves. R. Collin). Давид Позар же тоже более практическая книга, очень рекомендую (Microwave Engineering. D. Pozar).
Mogwaika
А какие есть подходы если полоса широкая?
И если для звука, нужно разбивать на узкие полосы и делать отдельные излучатели?
DryominG
Что Вы подразумеваете под полосой?