Завершив создание веб-архитектуры для нашего нового веб-комикса Meow the Infinite, я решил, что самое время написать несколько давно назревших технических статей. Данная статья будет посвящена фильтру, разработанному мной несколько лет назад. Он никогда не обсуждался в области сжатия видео, хотя мне кажется, что это стоит сделать.

В 2011 году я разработал “half-pel filter”. Это особый вид фильтра, который берёт входящее изображение и максимально убедительно отображает, как бы выглядело изображение при сдвиге ровно на полпикселя.

Вероятно, вы задаётесь вопросом, зачем вообще может понадобиться такой фильтр. На самом деле, они достаточно часто встречаются в современных видеокодеках. Видеокодеки используют подобные фильтры, чтобы брать фрагменты предыдущих кадров и использовать их в последующих кадрах. Более старые кодеки перемещали данные кадра только по целому пикселю за раз, однако новые кодеки пошли дальше и для лучшей передачи мелких движений позволяют выполнять сдвиг на половину или даже на четверть пикселя.

При анализе поведения алгоритмов компенсации движения в традиционных halfpel-фильтрах, Джефф Робертс выяснил, что при многократном применении к последовательным кадрам они быстро деградируют, заставляя другие части видеокомпрессора использовать для исправления артефактов больше данных, чем необходимо. Если отключить эти исправления и взглянуть на «сырые» результаты halfpel-фильтра, то такое исходное изображение:


превращается вот в такое:


всего спустя одну секунду видео. Как и должно, оно сдвинуто в сторону, потому что каждый кадр сдвигал изображение на полпикселя. Но результат выглядит не как перемещённая версия исходного изображения, он серьёзно искажён.

В течение «одной секунды видео» фильтр на самом деле применяется множество раз — 60, если видео воспроизводится с частотой 60 кадров в секунду. Но в идеале нам нужны фильтры, стойкие к подобным искажениям. Если бы у нас они были, то видео с плавной прокруткой не кодировались бы с таким количеством исправлений артефактов, благодаря чему стали бы меньше, или лучше качеством, или и то, и другое.

Если вы знакомы с областью сжатия видео, то можете задаться вопросом, зачем нам вообще применять halfpel-фильтр больше одного раза. В конце концов, если применить halfpel-фильтр дважды, то мы уже переместимся на один целый пиксель, так почему бы просто не использовать данные из двух кадров назад и просто не взять их?

Ответ не так прост. Во-первых, чем больше данных нам нужно для кодирования получения данных, тем меньшее сжатие мы получим. Поэтому если мы начнём кодировать без необходимости слишком много данных типа «из какого кадра брать данные», то видео будет сжиматься не очень хорошо.

Но это не самое важное. Основная проблема заключается в том, что если нам нужно брать информацию из предыдущих кадров, то придётся их хранить. Для сохранения двух предыдущих кадров вместо одного нужно, как можно догадаться, в два раза больше памяти. Для современных ЦП это не особая проблема, у них много памяти и такая мелочь их не волнует. Но это проблема для вас, если вы хотите создать быстрый, портируемый, широко применяемый формат видео, который должен работать в устройствах с малым количеством памяти (мобильных телефонах, встроенной электронике и т.д.).

Нам очень не хочется хранить несколько кадров с целью компенсации движения только для того, чтобы не применять halfpel-фильтр. Поэтому мне поручили выяснить, что же конкретно здесь происходит, и разобраться, смогу ли я создать фильтр, не имеющий таких проблем.

До этого я никогда не работал с фильтрами и понятия не имел, как обычно они разрабатываются. Как ни странно, это оказалось мне на пользу, потому что мне пришлось взглянуть на эту проблему без предубеждений.

Основы

Я быстро понял, что самые популярные halfpel-фильтры имеют схожую структуру: для получения каждого пикселя в выходном изображении берутся от 2 до 8 пикселей входящего изображения, которые сэмплируются и смешиваются с определёнными коэффициентами. Разные фильтры отличаются только количеством сэмплируемых исходных пикселей (часто на жаргоне разработчиков фильтров они называются tap) и коэффициентами смешивания пикселей. Эти коэффициенты часто называются «ядром фильтра» (filter kernel) и это всё, что необходимо для полного описания фильтра.

Если вам знаком любой вид сэмплирования или ресэмплирования изображений (например, масштабирование изображений), то это должно быть вам понятно. По сути, фильтры выполняют ту же задачу. Так как сжатие видео — это обширная область, в которой ведутся различные исследования, то очевидно, что существует множество других способов компенсации движения, кроме простой фильтрации. Но распространённые кодеки обычно используют процедуры компенсации движения с halfpel-фильтрами, которые по сути идентичны фильтрам масштабирования изображений: они просто берут исходные пиксели, умножают их на некие веса, складывают их и получают выходные пиксели.

Необходимость «резкости»

Итак, нам нужно сдвинуть изображение на полпикселя. Если вы программист графики, но не особо знакомы с фильтрацией, то можете подумать: «тоже мне проблема, просто используем билинейный фильтр». Это стандартный процесс в работе с графикой, когда нам нужно вычислить промежуточные значения между двумя входящими элементами данных, как происходит здесь.

Билинейный фильтр для движения ровно на полпикселя можно легко описать следующим ядром фильтра:

// NOTE(casey): Simple bilinear filter
BilinearKernel[] = {1.0/2.0, 1.0/2.0};

Это сработает, но не без проблем. Если ваша цель — высококачественные изображения, а в случае сжатия видео цель именно такая, то билинейный фильтр — не лучшее решение, потому что он добавляет в результат больше размытости, чем нужно. Её не так много, но больше, чем создают другие фильтры.

Чтобы показать это наглядно, вот приближенное изображение глаза моржа из исходного изображения после однократного применения самых распространённых фильтров:


Слева — оригинал, справа — билинейная фильтрация. Между ними самые широко применяемые halfpel-фильтры видеокодеков. Если присмотреться, то можно увидеть, что почти все изображения выглядят похоже, кроме билинейного, которое немного больше размыто. Хотя размытия не так много, если ваша основная цель — качество изображения, то этого достаточно, чтобы предпочесть билинейному фильтру другой фильтр.

Так как же другие фильтры «сохраняют» резкость и избегают размытия? Давайте вспомним, как выглядит ядро билинейного размытия:

BilinearKernel[] = {1.0/2.0, 1.0/2.0};

Оно очень простое. Чтобы сдвинуть изображение на половину пикселя, мы берём пиксель и смешиваем его на 50% с его соседом. Вот и всё. Можно представить, как это «размывает» изображение, потому что в тех местах, где яркий белый пиксель соседствует с тёмным чёрным, эти два пикселя при билинейной фильтрации усредняются, создавая серый пиксель, «смягчающий» границу. Это происходит с каждым пикселем, поэтому буквально каждый участок, где есть отчётливая разница в цвете или яркости. сглаживается.

Именно поэтому в качественных кодеках для компенсации движения не применяется билинейная фильтрация (хоть она может и использоваться в других случаях). Вместо неё применяются фильтры, сохраняющие резкость, например, такие:

// NOTE(casey): Half-pel filters for the industry-standard h.264 and HEVC video codecs
h264Kernel[] = {1.0/32.0, -5.0/32.0, 20.0/32.0, 20.0/32.0, -5.0/32.0, 1.0/32.0};
HEVCKernel[] = {-1.0/64.0, 4.0/64.0, -11.0/64.0, 40.0/64.0, 40/64.0, -11.0/64.0, 4.0/64.0, -1.0/64.0};

Как видите, там, где билинейная фильтрация учитывала только два пикселя, эти фильтры учитывают шесть (h.264) или даже восемь (HEVC) пикселей. Кроме того, они не просто вычисляют обычные взвешенные средние значения этих пикселей, а используют для некоторых пикселей отрицательные веса, чтобы вычитать эти пиксели из других значений.

Зачем они это делают?

Понять это на самом деле нетрудно: используя и положительные, и отрицательные значения, а также рассматривая более широкое «окно», фильтр способен учитывать разность между соседними пикселями и моделировать резкость двух ближайших пикселей относительно их более дальних соседей. Это позволяет сохранять резкость изображения-результата в тех местах, где пиксели значительно отличаются от своих соседей, в то же время по-прежнему используется усреднение для создания правдоподобных значений «полупиксельных» сдвигов, которые обязательно должны отражать сочетание пикселей из входящего изображения.

Нестабильная фильтрация

Итак, проблема решена? Да, возможно, но если вам достаточно только выполнить одно полупиксельное смещение. Однако эти фильтры «резкости» (и здесь я использую этот термин намеренно) на самом деле выполняют нечто опасное, по сути своей аналогичное тому, что делает билинейная фильтрация. Они просто лучше умеют это скрывать.

Там, где билинейная фильтрация снижает резкость изображения, эти стандартные фильтры повышают её, как операция «sharpen» в какой-нибудь графической программе. Величина повышения резкости очень мала, поэтому если выполнить фильтр только один раз, мы этого не заметим. Но если фильтрация выполняется несколько раз то это может стать очень заметным.

И, к сожалению, поскольку это повышение резкости процедурное и зависит от разности между пикселями, она создаёт петлю обратной связи, которая будет продолжать повышать резкость одной и той же границы снова и снова, пока не разрушит изображение. Можно показать это на конкретных примерах.

Сверху — оригинальное изображение, снизу — с билинейной фильтрацией, выполнявшейся в течение 60 кадров:



Как и можно было ожидать, размывание просто продолжает снижать резкость изображения, пока оно не становится довольно смазанным. Теперь вверху будет оригинал, а внизу — halfpel-фильтр кодека h.264, выполнявшийся в течение 60 кадров:



Видите весь этот мусор? Фильтр сделал то же самое, что и эффект «размытия» билинейной фильтрации, но наоборот — он «повысил резкость изображения» настолько, что все части, где были детали, превратились в сильно искажённые светлые/тёмные паттерны.

Ведёт ли себя лучше кодек HEVC, использующий 8 пикселей? Ну, он определённо справляется лучше, чем h.264:


но если мы увеличим время с 60 кадров (1 секунда) до 120 кадров (2 секунды), то всё равно увидим, что возникает обратная связь и изображение разрушается:


Ради тех, кому нравится обработка сигналов, я добавлю для справки ещё и windowed-sinc-фильтр (который называется фильтром Ланцоша (Lanczos filter)):

// NOTE(casey): Traditional 6-tap Lanczos filter
LanczosKernel[] = {0.02446, -0.13587, 0.61141, 0.61141, -0.13587, 0.02446};

Я не буду объяснять в этой статье, почему кого-то может заинтересовать «windowed sinc», но достаточно сказать, что этот фильтр популярен по теоретическим причинам, поэтому посмотрите, как он выглядит при обработке 60 кадров (1 секунда):


и при обработке 120 кадров (2 секунды):


Лучше, чем h.264, и примерно так же, как HEVC.

Стабильная фильтрация

Как мы можем добиться лучших результатов, чем h.264, HEVC и windowed sinc? И насколько лучше они могут быть?

Подобные вопросы я ожидал бы увидеть в литературе по сжатию видео и они должны быть хорошо известны специалистам по сжатию, но, на самом деле (по крайней мере, на 2011 год) я не нашёл никого, кто хотя бы заявил, что это проблема. Поэтому мне пришлось придумывать решение в одиночку.

К счастью, формулировка задачи очень проста: создать такой фильтр, который можно применить как можно больше раз, чтобы изображение при этом выглядело приблизительно так же, как в начале.

Я называю это определение «стабильной фильтрацией», потому что, по моему мнению, оно может считаться свойством фильтра. Фильтр «стабилен», если он не попадает в свою петлю обратной связи, то есть его можно применять многократно без создания артефактов. Фильтр «нестабилен», если он создаёт артефакты, которые усиливаются при многократном применении и со временем разрушают изображение.

Повторюсь, я не понимаю, почему эта тема не рассматривается в литературе по видеокодекам или обработке изображений. Возможно, в ней используется другая терминология, но я её не встречал. Понятие «обратной связи» хорошо устоялось в области работы со звуком. но не является важной проблемой в обработке изображений. Возможно потому, что обычно фильтры должны применяться только один раз?

Если бы я был специалистом в этой области, то у меня скорее всего имелось мнение по этому поводу, и возможно я бы даже знал те закоулки специализированной литературы, где уже существуют решения этой проблемы, известные немногим. Но, как я уже сказал в начале статьи, раньше мне никогда не доводилось заниматься созданием фильтров, поэтому я искал только в широко известных статьях (хотя стоит заметить, что есть как минимум один человек, хорошо известный в литературе, который тоже ничего подобного не слышал).

Итак, с утра мне сказали, что нам нужен этот фильтр, и весь день я пытался его создать. Мой подход был простым: я создал программу, выполнявшую фильтр сотни раз и в конце выдававшую изображение, чтобы я мог увидеть результат длительных прогонов. Затем я экспериментировал с разными коэффициентами фильтра и наблюдал за результатами. Это в буквальном смысле был направленный процесс проб и ошибок.

Примерно час спустя я подобрал наилучшие коэффициенты фильтра, подходящие для этой задачи (но у них был один изъян, о котором я расскажу во второй части статьи):

MyKernel[] = {1.0/32.0, -4.0/32.0, 19.0/32.0, 19.0/32.0, -4.0/32.0, 1.0/32.0};

Это ядро находится на грани между повышением резкости и размытием. Поскольку повышение резкости всегда приводит к обратной связи, создающей яркие и очевидные артефакты, это ядро фильтра предпочитает небольшое размытие, чтобы изображение просто выглядело немного более «тусклым».

Вот как оно выглядит после 60 кадров. Для справки я показал все фильтры в таком порядке: оригинальное изображение (без фильтрации), мой фильтр, билинейный, Lanczos, h.264, HEVC:







Как видите, мой фильтр даёт немного более размытые результаты, чем фильтры повышения резкости, но не имеет неприемлемых артефактов резкости спустя 60 кадров. Однако, вы, возможно предпочтёте артефактам размытия артефакты повышения резкости, поэтому можете выбирать между самым лучшим фильтром повышения резкости (Lanczos) и моим. Однако если мы повысим количество до 120 кадров, то мой фильтр оказывается вне конкуренции:







После 300 кадров все фильтры, за исключением моего, становятся похожими на плохую шутку:







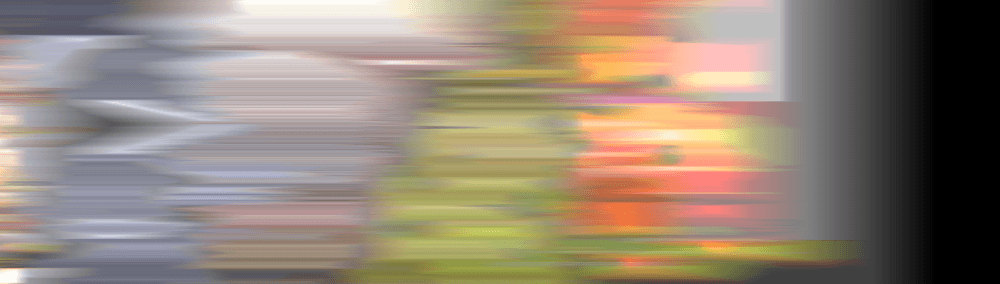
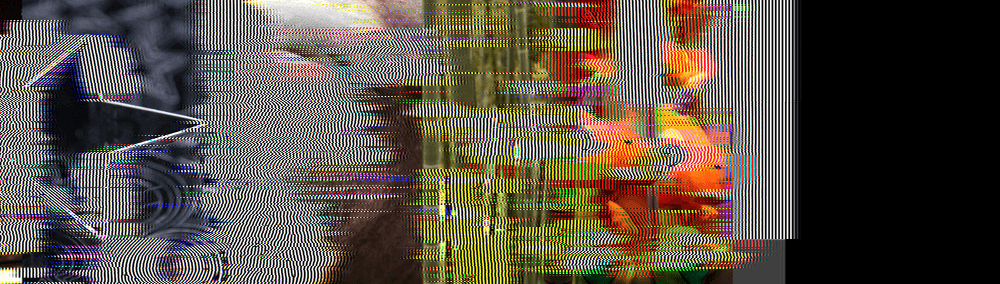
Спустя 600 кадров шутка становится ещё более жестокой:







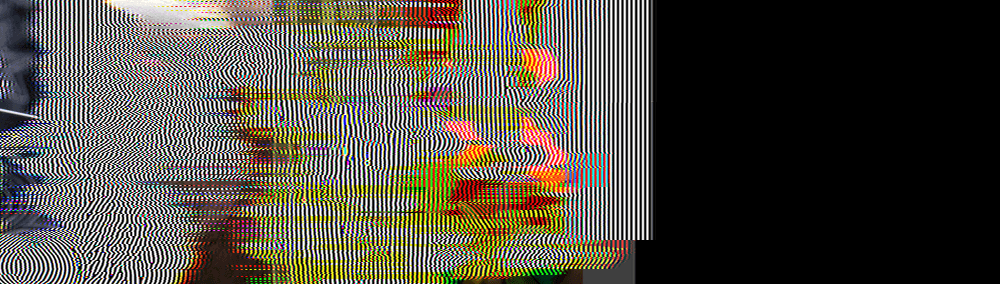
Можно даже и не говорить, что происходит через 900 кадров:

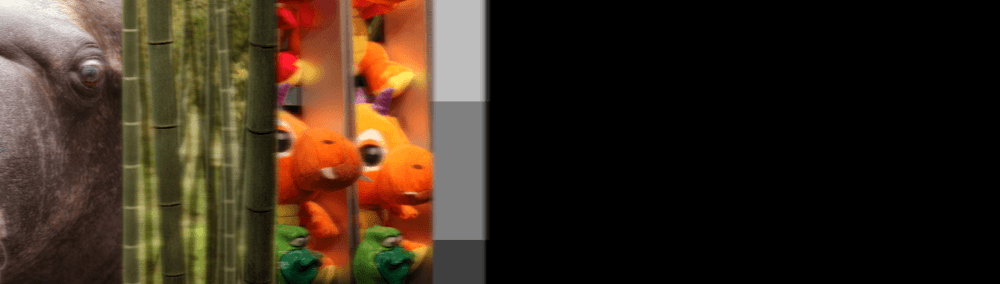
Насколько он стабилен?

На этом этапе естественно будет задаться вопросом: мой фильтр на самом деле стабилен, или это просто очень медленное размытие, гораздо медленнее, чем у билинейной фильтрации? Возможно, после тысяч повторений мой фильтр постепенно размоет изображение?

Как ни удивительно, но ответ, похоже, отрицательный. Хотя в течение примерно сотни первых наложений добавляется немного размытия, похоже на то, что фильтр сходится к стабильному представлению изображения, которое затем никогда не деградирует. Вот ещё одно увеличенное изображение глаза моржа:


Слева направо: оригинальное изображение, мой фильтр, применённый 60 раз, 120 раз, 300 раз, 600 и 900 раз. Как видите, размытие сходится к стабильному состоянию, которое больше не деградирует даже после сотен наложений фильтра. Для контраста сравним это с windowed sync при том же количестве сэмплов (tap), и увидим, насколько плохо (и быстро!) артефакты образуют обратную связь и создают бесполезный результат:


Мой фильтр кажется очень стабильным, и по сравнению со всеми увиденными мной фильтрами создаёт наилучшие результаты после многократного применения. Похоже, он имеет некое свойство «асимптотичности», при котором данные быстро сходятся к (ограниченно) сглаженному изображению, а затем это сглаженное изображение сохраняется, и не выполняет неограниченную деградацию к полному мусору.

Я даже пробовал накладывать фильтр миллион раз, и похоже, что после первых нескольких сотен наложений он дальше не деградирует. Без более качественного математического анализа (а я пока не нашёл математического решения, способного доказать это совершенно точно, но я точно знаю, что оно где-то есть), я не могу сказать с уверенностью, что где-то спустя миллиарды или триллионы наложений что-нибудь не сломается. В пределах разумного тестирования мне не удалось обнаружить дальнейшей деградации.

Является ли он наилучшим стабильным Halfpel-фильтром для шести tap-ов?

На этом этапе логично будет задать вопрос: действительно ли это лучшее, что можно найти? Интуиция подсказывает нам, что нет, потому что совершенно не имея никаких знаний о разработке фильтров и почти не заглядывая в литературу, я подобрал этот фильтр всего за час. По крайней мере, можно предположить, что после такого краткого исследования я бы не нашёл окончательно-наилучший-всепобеждающий-великолепный фильтр.

Верно ли это предположение? И если верно, то каким будет окончательный наилучший фильтр? Подробнее я расскажу об этом во второй части статьи.