Добрый день. Эту статью я написал специально для студентов курса «Алгоритмы для разработчиков» в OTUS и сегодня хочу поделиться ею со всеми читателями нашего блога.

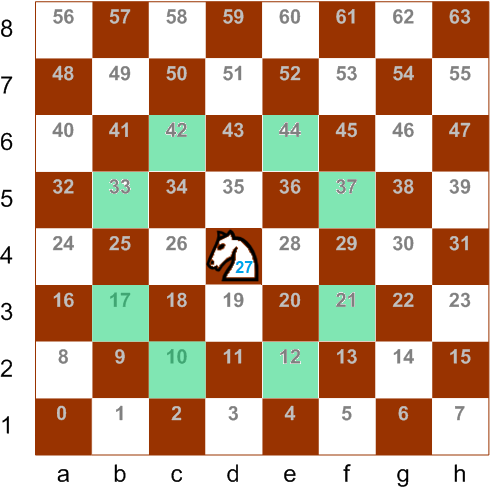
Шахматный конь стоит на шахматной доске и задумчиво смотрит в шахматную даль.
Сколько разных ходов он может сделать?



Хвала изобретателю шахмат, на доске 64 клетки.
Хвала архитектору компьютеров — у типа ulong тоже 64 бита.
Это же надо было случиться такому совпадению!
Напрашивается гениальная идея — хранить всю доску в одном целом числе! Для этого решения существует даже специальный термин — Bitboard — битовая доска.

Так как же быстро найти количество ходов шахматного коня, используя эту идею?

Дано: knightNr — номер клетки доски, где стоит конь (от 0 до 63).
Надо: movesCount — количество полей, куда он может пойти (от 2 до 8).

Алгоритм.

1.Конвертировать номер клетки коня в ulong-значение битовой доски
knightNr -> knightBits

2.Установить биты для всех возможных ходов коня
knightBits -> movesBits

3.Подсчитать количество единичных битов
movesBits -> movesCount



Первый шаг выполняется очень просто, нужно нулевой бит сдвинуть влево на указанное количество позиций.

	ulong knightBits = 1 << knightNr;

Второй шаг немножко сложнее. Конь может пойти в 8 разных сторон. Мы будем считать эти смещения не «по горизонтали/вертикали», а по битовым позициям. То есть, считаем, на сколько позиций нужно сместить стартовый бит для каждого хода. Потом всё «складываем» операцией логического «или».

Начнём перечислять ходы от левой стороны доски к правой:

  movesBits = knightBits <<  6 | knightBits >> 10 // на b5 и b3
            | knightBits << 15 | knightBits >> 17 // на c6 и c2
            | knightBits << 17 | knightBits >> 15 // на e6 и e2
            | knightBits << 10 | knightBits >>  6 // на f5 и f3; 

Правда, классно!?

К сожалению, по краям доски есть «чёрные дыры». Например, по этому алгоритму из клетки a4 (бит #24) можно попасть на клетку g2 (бит #14 = 24 — 10), этот прыжок является телепортацией сферического шахматного коня в вакууме на доске сквозь чёрную дыру крайние вертикали…

Чтобы исключить квантовый скачок коня через край доски, необходимо «отключать» крайние полосы после перемещения. Например, для ходов +6 и -10 (влево на две клетки) необходимо аннулировать полученные значения на вертикалях g и h, так как на этих вертикалях нельзя оказаться после перемещения «влево» на два хода.

Для этого нам понадобится 4 константы битовых сеток, в которых все биты установлены в 1, кроме указанных вертикалей. А именно:

        ulong nA  = 0xFeFeFeFeFeFeFeFe;
        ulong nAB = 0xFcFcFcFcFcFcFcFc;
        ulong  nH = 0x7f7f7f7f7f7f7f7f;
        ulong nGH = 0x3f3f3f3f3f3f3f3f;

Сверху и снизу шахматной доски тоже есть «чёрные дыры», которые полностью поглощают коня, поэтому отдельно их проверять не нужно.

Теперь алгоритм генерации допустимых ходов коня выглядит так:

   movesBits = nGH & (knightBits <<  6 | knightBits >> 10)
             |  nH & (knightBits << 15 | knightBits >> 17)
             | nA  & (knightBits << 17 | knightBits >> 15)
             | nAB & (knightBits << 10 | knightBits >>  6);

Это работает очень (!) быстро.

Несколько тиков — и у нас битовая карта всех возможных похождений коня. Самое удивительное, что этот алгоритм отлично работает, даже если на доске расположено несколько коней. Он за один раз генерирует все возможные ходы для всех коней! Правда, здорово!?

Осталось подсчитать количество бит

Самый простой способ — сдвигать число на 1 бит вправо и считать единички. Сложность — 64 операции. Память — 64 бита.

Самый быстрый способ — создать кэш/массив на 65536 элементов, в котором записано количество битов для каждого индекса от 0 до 65535. И сложить 4 элемента из этого массива, которые соответствуют очередным 16-битовым сегментам числа.
Сложность — 4 операции. Память — 64 килобайта.

Но мы рассмотрим самый хитрый способ, сложность которого равна количеству единичных битов в числе. Поскольку ходов не так много, то этот подход для нас будет самым оптимальным.

Для начала заметим, что вычитая единицу из числа, мы превращаем все «правые» нули в единицы, а самую крайнюю единицу в нуль:

1001010100010000 - 1 =
1001010100001111

Далее применим операцию логического «и» для этих чисел:

1001010100010000 &
1001010100001111 =
1001010100000000

Как видите, таким хитрым способом мы сбросили в нуль самую правую единицу. Повторяем эту операцию, пока не получим в результате нуль. Сколько итераций, столько и единичных битов. Правда, здорово!?

Вот как записывается этот алгоритм полностью:

        int movesCount = 0;
        while (movesBits != 0)
        {
            movesBits &= (movesBits - 1);
            movesCount ++;
        }

Задача решена!

У этой задачи есть другое, очень простое, чисто логическое решение: определить удалённость коня от края шахматной доски (в углу 2 хода, возле края от 3 до 6 ходов, в центре 8 ходов). Но если бы мы решали задачу «в лоб» таким образом, то не узнали бы про битовую доску, про вертикальные битовые маски, про алгоритм быстрого подсчёта единичных битов и про чёрные дыры для сферических коней в вакууме…

Теперь мы про это всё знаем. Жизнь шахматного программиста стала более богатой и осмысленной, ура!

Самостоятельное задание: сделайте то же самое для Шахматного короля.