Один из самых необычных алгоритмов сортировки массива  - это HeapSort, в основе которого лежит алгоритм сортировки выбором, используется структура данных «куча» для быстрого нахождения максимального элемента, а также способ хранения двоичного дерева в линейном массиве. Разберёмся со всем по порядку.

Сортировка выбором

За основу работы синхрофазотрона алгоритма сортировки выбором положен принцип нахождения максимального элемента в неотсортированной части массива и переноса его в отсортированную. 

Для нахождения максимального элемента в неотсортированной части массива необходимо пересмотреть все элементы из этой части, на это потребуется К операций сравнения и не более К операций присваивания для запоминания номера максимального элемента. Здесь К - размер левой части массива. 

Для переноса элемента в отсортированную часть достаточно обменять найденный максимальный элемент с последним элементом неотсортированной части, после чего он станет первым элементом отсортированной части, размер которой увеличится на 1. 

После каждой итерации размер неотсортированной части уменьшается, поэтому всего необходимо сделать N итераций. Посчитаем, сколько всего действий необходимо выполнить для сортировки массива:

(2*N  + 1) + (2*(N - 1) + 1) + …
+ (2*K + 1) + … + 2*1 + 1 =
= 2(N*N - N)/2 + N = N*N

То есть, сложность алгоритма сортировки выбором - O(N²).

Пирамидальная сортировка

Попробуем ускорить время работы алгоритмы сортировки.

Больше всего времени уходит на поиск максимального элемента в неотсортированной части. Можно ли как-нибудь ускорить этот процесс? Да, можно, если использовать структуру данных «куча» или «пирамида». Это древовидная структура данных, в которой каждый дочерний элемент меньше родительского. На вершине кучи всегда находится максимальный элемент, поэтому его можно выбрать максимально быстро - всего за 1 операцию.

Идея замечательная, но для её воплощения нужно решить ряд технических вопросов:

1. создать древовидную структуру

2. сформировать кучу из неотсортированных элементов

3. уменьшить размер кучи после переноса максимума в отсортированную часть

Создание древовидной структуры для кучи

Поскольку мы можем сравнивать только два числа друг с другом, то лучше всего для кучи создать полное двоичное дерево. Для его хранения не обязательно создавать отдельную структуру со ссылками на дочерние элементы, благодаря тому, что двоичное дерево полностью заполнено и нам не потребуется изменение его структуры, то исходный массив вполне подойдёт для этой цели. Нужно только определить формулы для перехода к родительскому и к дочерним элементам.

P = (x - 1) / 2
L = 2x + 1
R = 2x + 2

Формирование кучи из неотсортированных элементов

Единственное правило кучи: дочерние элементы меньше родительских. 

Давайте опишем рекурсивный алгоритм 

void heapify(int root, int size) 

который превращает в кучу заданное поддерево, при условии, что дочерние поддеревья уже являются корректными кучками. Для этого в заданном поддереве нужно изменить порядок расположения элементов - корневого и двух дочерних.

Откуда начать формирование кучи?

У листьев дерева нет дочерних элементов, поэтому, они сразу удовлетворяют правилам и являются маленькими «кучками» из одного элемента. Поэтому мы можем пропустить все листовые элементы и начать формирование кучи с первого внутреннего узла -- им является родитель последнего листа.

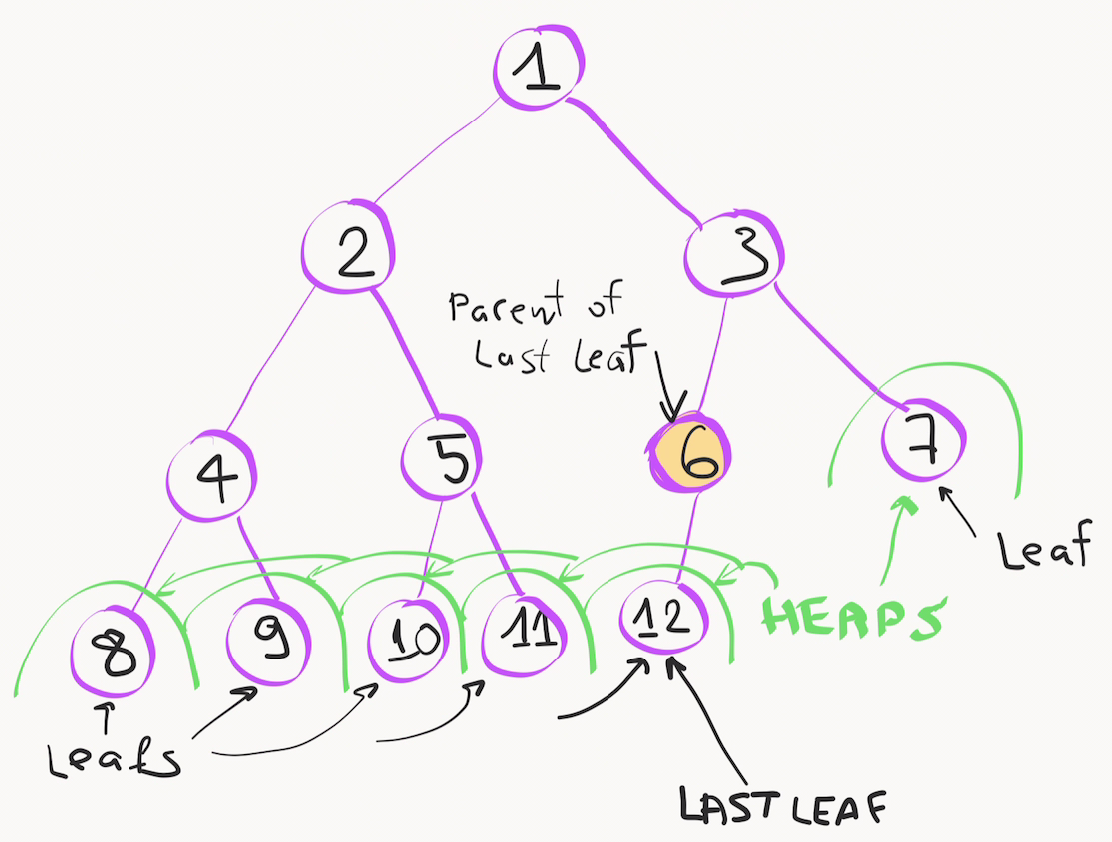
Если значение внутреннего узла больше его дочерних элементов - всё в порядке, можно переходить к предыдущему элементу, пока не дойдём до корня.

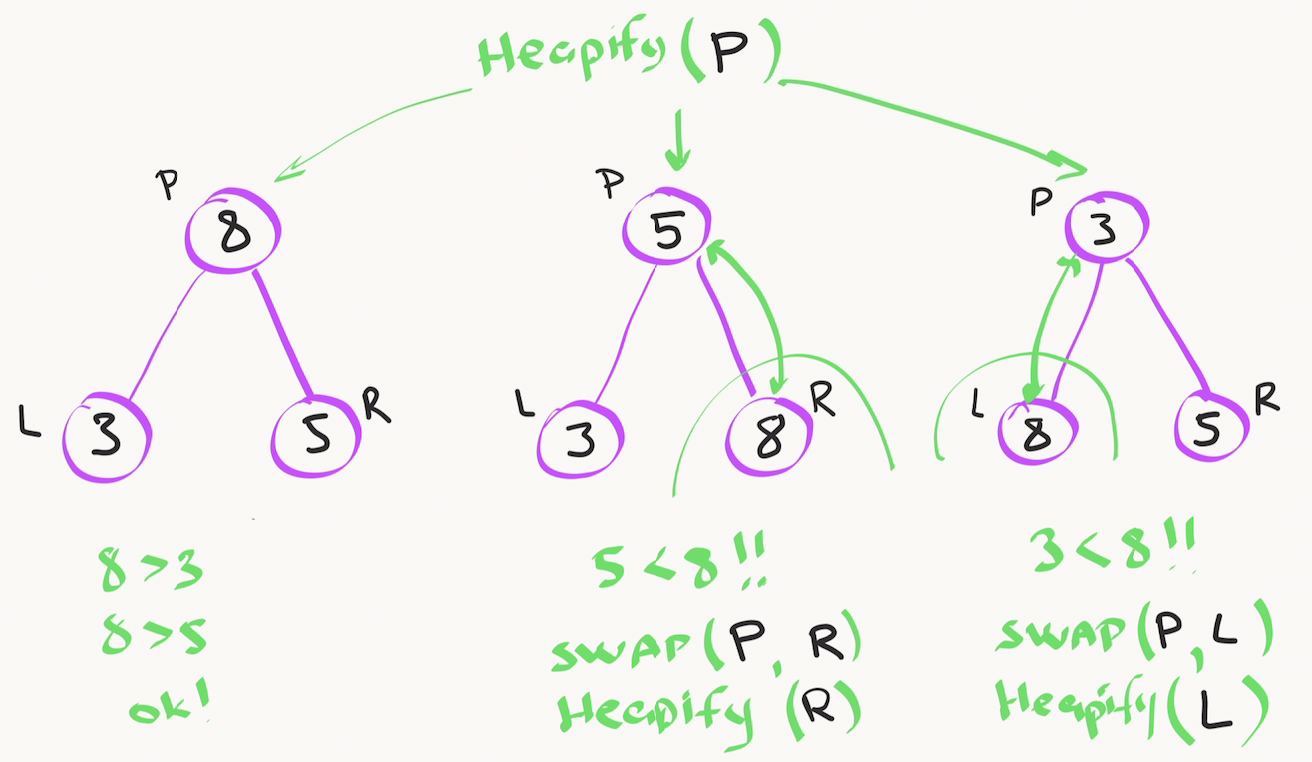
В противном случае нужно обменять значение внутреннего узла с тем дочерним элементом, в котором находится локальный максимум. После операции обмена мы должны рекурсивно запустить наш алгоритм heapify для изменённого дочернего узла, так как новое значение стало меньше, из-за чего у наших внуков может оказаться значение больше, чем у сына, это надо проверять и исправлять.

Будем продолжать вызывать функцию heapify() для всех элементов вплоть до корневого. Таким образом мы итеративно превратим неотсортированную часть массива в правильную кучу. 

Сколько операций необходимо на этот процесс? Давайте рассмотрим на конкретном примере. Допустим, у нас 31 элемент в массиве. В нижней строчке 16 листов и мы их все пропускаем, получается 0*16 операций. Во второй строчке снизу у нас 8 элементов, и в каждом нужно будет выполнить одно действие, получается 1*8 операций. На третей строчке снизу - 4 элемента, в каждой строчке будет не более 2 действий, так как глубина везде 2, получается 2*4 операций. На следующей строке - 3*2, на верхней - 4*1. Сложим всё вместе:

0*16 + 1*8 + 2*4 + 3*2 + 4*1 = 34 операций.

В самом деле, на каждом новом уровне в два раза меньше элементов, а максимальная глубина увеличивается только на 1, то есть амортизированная сложность формирования кучи - O(N).

Класс HeapSort с алгоритмом сортировки

Перенос максимума в отсортированную часть и уменьшение кучи

Самое простое и быстрое действие. Максимальный элемент всегда находится на вершине кучи. Его нужно обменять с последним листом кучи, который сразу переходит в отсортированную часть массива. Размер кучи после этого уменьшится на 1, а на вершине кучи окажется один из самых меньших значений массива, поскольку там оказался листовой элемент.

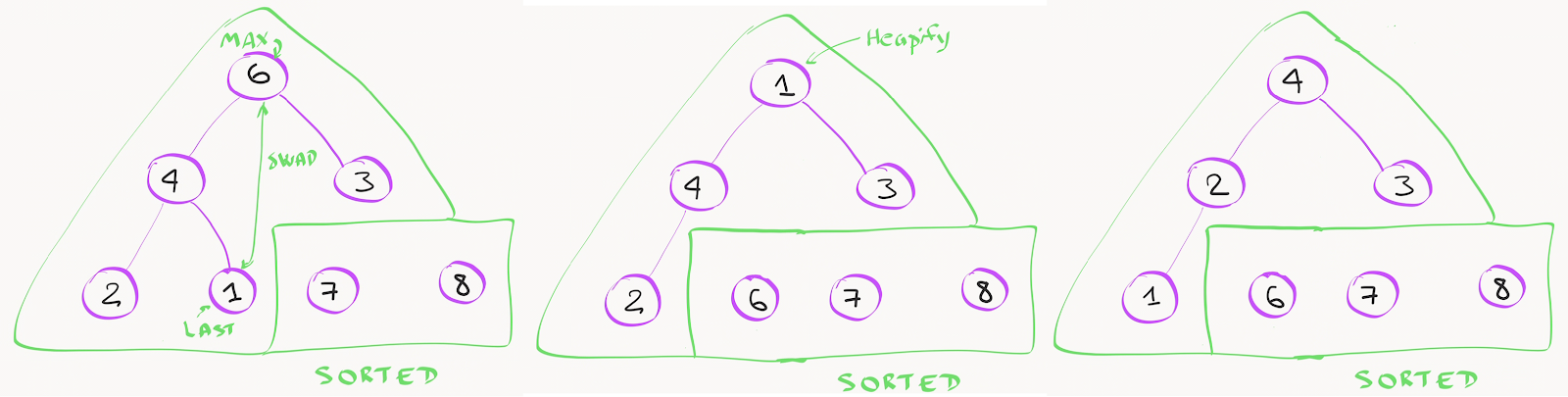
Теперь нам нужно «перепирамидить» кучу -- вызвать алгоритм проверки для вершины, в процессе которого будут выполняться рекурсивные вызовы проверки для дочерних элементов, пока это будет необходимо. В худшем случае на это потребуется log 2 K операций, где K - текущий размер пирамиды.

После N итераций пирамида исчезнет, все элементы окажутся в отсортированной части, сортировка завершена!

Сложность сортировки не превышает O(N log 2 N).

В этой статье мы познакомились с одним из самых интересных алгоритмов сортировки - Пирамидальная сортировка - в которой используется структура данных «куча» для быстрого нахождения максимального элемента, а также способ хранения двоичного дерева в линейном массиве.

Статья была подготовлена в рамках набора на курс "Алгоритмы и структуры данных". 20 апреля я проведу бесплатный демо-урок на котором мы сначала реализуем алгоритм сортировки выбором, а потом превратим массив в пирамиду (кучу) и ускорим время поиска максимального элемента в неотсортированной части массива с линейного до логарифмического. В итоге у нас получится алгоритм Пирамидальной сортировки. Мы наглядно продемонстрируем работу алгоритма на визуальных примерах с конкретными числами. Участие в демо-уроке абсолютно бесплатное.

Регистрация доступна по ссылке.