Похоже, что плитки Вана также способны исполнять машины Тьюринга, и следовательно, они Тьюринг-полны, а значит, могут выполнять любую программу.
Это удивительное и непонятное заявление, поэтому в данном посте я немного исследую этот вопрос.
Вкратце о плитках Вана
Плитки Вана — это прямоугольные тайлы, у которых каждая из граней может соответствовать только другим конкретным граням, но для любой конкретной грани есть несколько возможных тайлов, которые могут соответствовать этой грани. Под соответствием граней я подразумеваю, что они соединяются бесшовно, не создавая никаких визуальных артефактов и признаков наличия шва между тайлами.
Это полезное для графики свойство, потому что оно позволяет создавать бесшовную тайловую графику, но конфигурация расположения тайлов при этом может быть полностью рандомизирована при условии, что все грани совместимы друг с другом. В результате получается тайловая графика, которая совсем не похожа на повторяющуюся, потому что визуальные паттерны становятся гораздо менее заметными, чем у традиционной тайловой графики.
Графические примеры, более подробную информацию и ссылки на Shadertoy можно найти здесь: Wang Tiling.
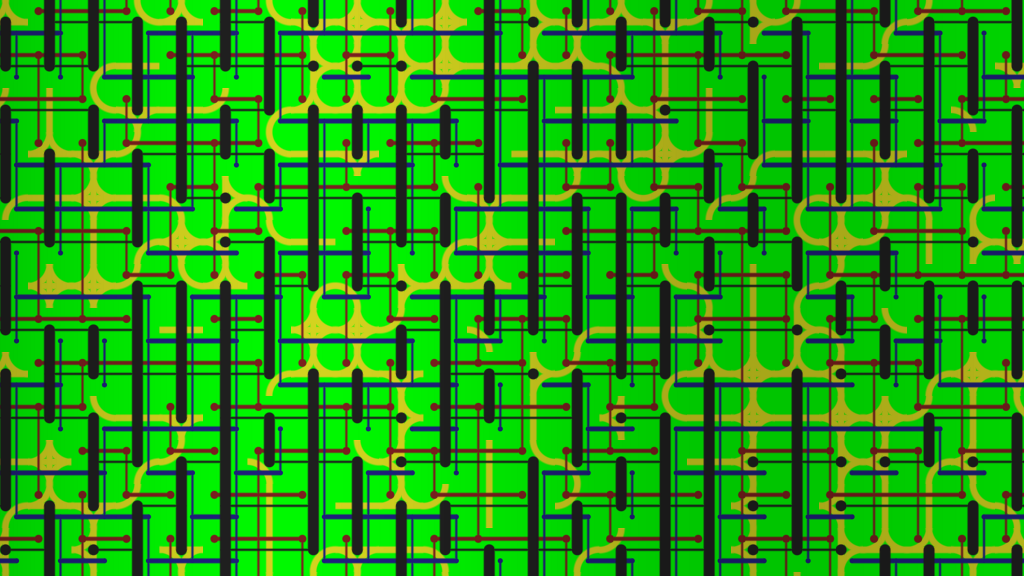
Вот созданный мной пример. Моя графика — это «арт программиста», но надеюсь, идея понятна. Рисунок составлен из 16 тайлов, и для каждой грани есть два различных типа граней.
Вкратце о машинах Тьюринга
Машины Тьюринга были изобретены в 1936 году Аланом Тьюрингом как обобщённая вычислительная машина, для которой доказано, что она может выполнять любой алгоритм.
Машина Тьюринга составлена из нескольких основных компонентов: ленты памяти, головки для чтения-записи и машины состояний.
Лента памяти имеет бесконечную длину, то есть имеет бесконечный объём накопителя, и в начале инициализируется одними нулями.
Головка чтения/записи начинает с определённой позиции ленты и может считывать/записывать значения, а также перемещаться по ленте влево и вправо.
Машина состояний управляет головкой чтения-записи.
Машина состояний знает, в каком состоянии она находится, и имеет правила относительно того что делать в каждом состоянии, когда она считывает значение с ленты.
Например, в состоянии A, если с ленты считан 0, то правило может заключаться в записи 1 в текущую позицию ленты, перемещении головки чтения-записи вправо, или в переходе к состоянию B. Состояние B может иметь совершенно иную логику и может или выполнять переход обратно к состоянию A, или оставаться в состоянии B, или перемещаться в совершенно другое состояние.
При помощи такой простой логики перехода между состояниями можно выполнить любой компьютерный алгоритм.
В машине Тьюринга также может быть «заключительное состояние» (Halt State), означающее, что программа завершила выполнение и ответ был вычислен.
Глядя на некоторые программы. можно легко увидеть. что со временем они завершаться или будут находиться в бесконечном цикле и никогда не остановятся. Некоторые программы находятся между ними, они сложны и в них не так легко определить, остановятся ли они когда-нибудь. Тьюринг доказал, что не существует общего решения, позволяющего определить, остановится ли машина Тьюринга (она же компьютерная программа), и это называется проблемой остановки. В общем случае единственный способ узнать, остановится ли программа — подождать. То есть по сути в общем случае ответами на этот вопрос являются или «да», или «пока ещё нет», однако в случае многих конкретных программ можно увидеть, что после запуска со временем они завершатся.
Вычисления на плитках Вана
Оказывается, плитки Вана могут симулировать машину Тьюрнга, то есть они «Тьюринг-полные», а значит, способны выполнять любой компьютерный алгоритм.
Чтобы реализовать это, нам понадобится столбец плиток Вана, обозначающий состояние машины Тьюринга в определённый момент времени, начиная со времени 0 в самом левом столбце. Мы будем помещать тайлы в столбец справа с учётом всех правил граней, а затем создавать столбец справа от него, и так далее, пока программа не завершится (или будем делать это вечно, если она не завершится). Если выбрать правильный набор плиток, то проверки на соответствие правилам граней в процессе расположения плиток будет достаточно для выполнения машины Тьюринга.
Давайте рассмотрим простой пример, в котором имеются следующие правила логики машины состояний:
- Когда машина находится в состоянии A, то в случае считывания 0 мы записываем 1, перемещаем головку чтения-записи вниз и переходим в состояние B.
- Когда машина находится в состоянии A, то в случае считывания 1 программа останавливается (переходит в заключительное состояние).
- Когда машина находится в состоянии B, то в случае считывания 0 мы записываем 1, перемещаем головку чтения-записи вверх и переходим в состояние A.
- Когда машина находится в состоянии B, то в случае считывания 1 программа останавливается (переходит в заключительное состояние)
Накопитель на ленточной памяти
В первую очередь нам нужно постоянное хранилище памяти для ленты. Для этого нам понадобятся две следующих плитки:
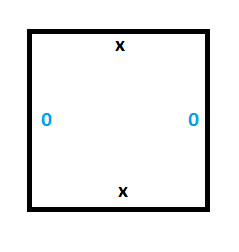
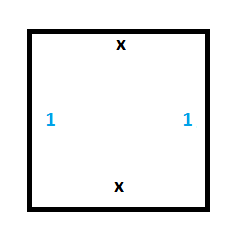
Чтобы проверить их работу, мы можем подготовить сегмент ленты с какими-то значениями (создать столбец плиток Вана) и убедиться, что единственные подходящие плитки Вана, располагаемые рядом с начальным столбцом — это плитки, переносящие значения 0 и 1 вперёд во времени, не изменяя их.
На показанной ниже схеме мы инициализируем ленту значением 0101 в самом левом столбце (time 0). Располагая только плитки с совместимыми гранями, мы видим, что значения в памяти сохраняются вечно. Мы реализовали накопитель памяти!

Мы начнём демонстрировать наш пример с памяти, инициализированной одними 0, а рисунок выше просто показывает постоянство памяти.
Машина состояний головки чтения-записи
Головка чтения-записи машины Тьюринга представлена как часть информации граней. Таким образом, кроме грани, хранящей 0 или 1, если в ней находится головка чтения-записи, то она также хранит состояние машины состояний.
В нашем примере используется два состояния (не включая заключительное состояние): A и B. Если считывается 1, то в любом из состояний (A или B) программа завершается.
Чтобы обработать это, нам нужны следующие плитки:
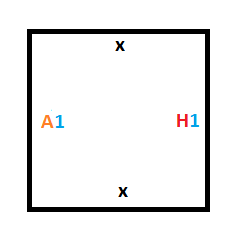
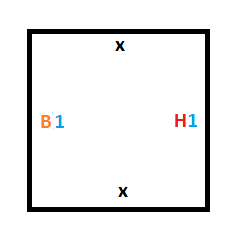
Теперь, когда у нас есть правила перехода в заключительное состояние, (правила 2 и 4), нам нужно понять, как реализовать правила, управляющие переключением из одного состояния в другое (правила 1 и 3).
Перемещение головки чтения-записи
Правило 1 гласит, что если мы находимся в состоянии A и считываем 0, то должны записать 1, переместить головку чтения-записи вниз и перейти в состояние B.
Нам нужно, чтобы эта плитка вызывала чтение 0 в состоянии A, чтобы записывать 1 в качестве вывода, и приказывать плитке ниже переходить в состояние B.
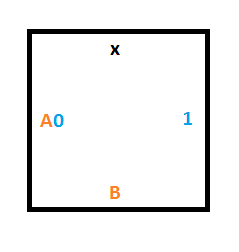
Плитка ниже текущей может иметь значение 0 или 1; не зная конкретного значения, мы должны сохранить его, но принять головку чтения-записи и находиться в состоянии B. Для этого нам необходимы две плитки — одна для 0 на ленте в этой позиции, другая для 1 на ленте.
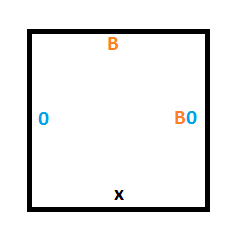
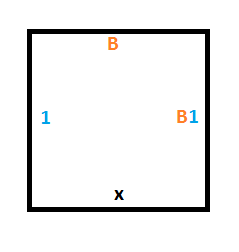
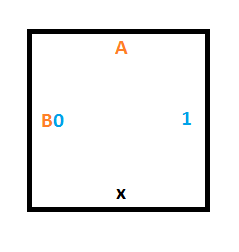
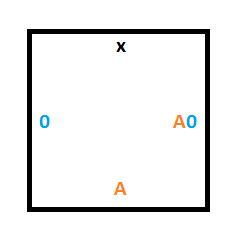
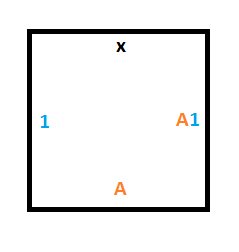
Правило 3 гласит, что если мы находимся в состоянии B и считываем 0, то должны записать 1, переместить головку чтения-записи вверх и перейти в состояние A.
Для этого нам нужна конструкция, похожая на конструкцию для правила 1, но перемещаемся мы не вниз, а вверх. Нужный результат дадут следующие три плитки:
Начальные плитки столбцов
Мы будем воспринимать границы области симуляции так, как будто они имеют грани «x».
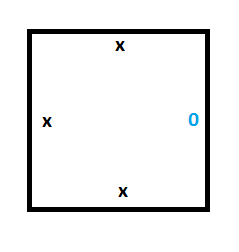
Это значит, что для создания начального столбца (машины Тьюринга во время 0) нам понадобится две специальные плитки. Одна плитка нужна для хранения на ленте значения 0, которым инициализируется лента, а другая плитка — для хранения позиции головки чтения-записи в состоянии A, являющемся нашим начальным состоянием.
Вот эти две плитки:
Готовый набор плиток
Вот полный набор из 12 плиток, который мы будем использовать:

Полная симуляция
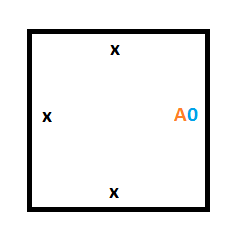
Вот исходная конструкция нашей машины Тьюринга во время 0. Заметьте, что это одно из возможных начальных состояний, но это то состояние, которое мы выбрали. Мы не оставляем случайности выбирать, с чего начинает головка чтения-записи, да и её наличие тоже. Если мы будем следовать только правилам граней, то можем получить 4 или 0 головок чтения-записи, или любое число между ними.

Отсюда для создания второго столбца мы начинаем сверху и движемся вниз, выбирая плитку, соответствующую ограничениям грани, которой он касается. На этом первом шаге головка считывает 0, записывает 1, перемещается вниз и переходит в состояние B.
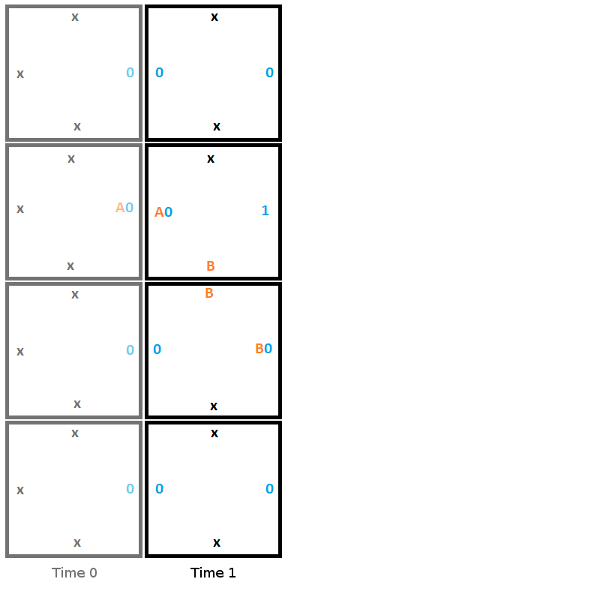
Вот второй шаг, где головка считывает 0, записывает 1, перемещается вверх и переходит в состояние A.
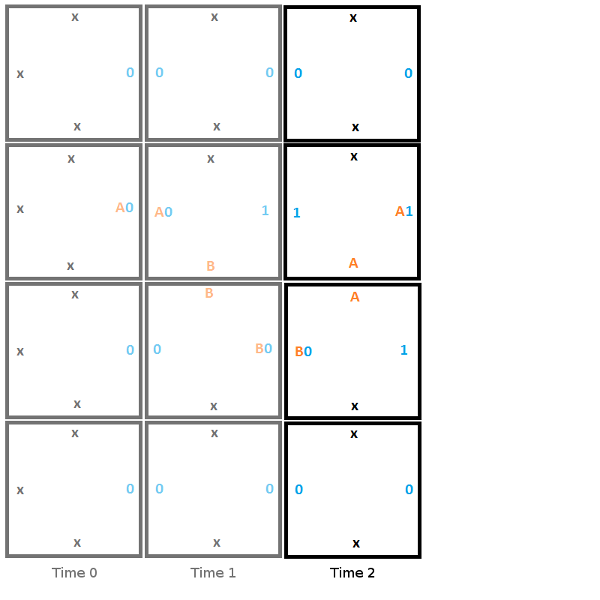
Вот последний шаг, на котором головка считывает 1 и переходит в заключительное состояние, обозначающее, что программа завершена.
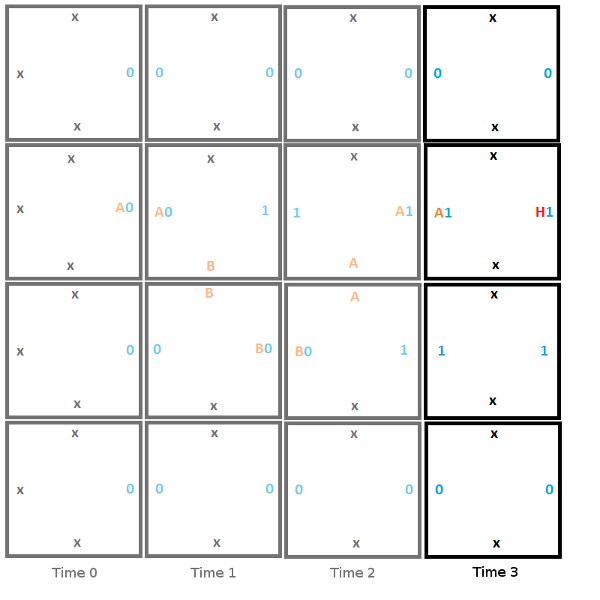
Программа завершилась и выдала нам выходное значение 0110, или 6. Эти выходные значения не особо значимы, но другие программы могут выдавать значимые выходные данные. Например, мы можем заставить машину Тьюринга сложить два числа, и выходными данными будет сумма этих двух чисел.
Важная деталь
Здесь нужно упомянуть важную деталь, которую мы не рассматривали выше, и о которой не говорится в большинстве объяснений машин Тьюринга на плитках Вана.
При размещении второй плитки для времени 2 единственным ограничением от граней является то, что плитка должна иметь x сверху и 1 слева. По сути, из-за этого ситуация становится неоднозначной, потому что неясно, какую из двух показанных ниже плиток нужно выбрать.


Тогда как нам выбрать правильную?
Ответ заключается в том, что мы просто делаем предположение и выбираем одну из них. Если в таком случае выбрана неверная плитка, то когда мы переходим к следующей плитке, будем искать плитку, у которой x сверху и B0 слева. Такой плитки не существует, поэтому поставить плитку мы не можем. Когда такое происходит, нам нужно вернуться к последней плитке и попробовать один из других возможных вариантов.
То есть, к сожалению, при симуляции машин Тьюринга с помощью плиток Вана в буквальном смысле присутствует процесс проб и ошибок, но, по крайней мере, он вполне поддаётся управлению. Он действительно немного усложняет вычисления в пиксельном шейдере (или в других устройствах с высокой параллелизацией), но затраты оказываются ненамного больше.
Вывод и ссылки
По некоторым представленным ниже ссылкам обсуждаются плитки Вана и машины Тьюринга, но обсуждения, похоже, не строго придерживаются машин Тьюринга. Например, вы можете заметить, что в некоторых примерах данным разрешают возвращаться «назад во времени» — когда программа завершается, ответ находится на ленте во время 0 машины Тьюринга, несмотря на то, что этих данных на самом деле не было там во время 0. Это показывает, что плитки Вана могут выполнять вычисления сами по себе, а не только симулируя машины Тьюринга, но я не знаю точно, как будет называться такая техника.
Кроме того, если вам интересно знать, что полезного в вычислениях при помощи плиток Вана, то лично я не смогу представить случаев их практического применения. Однако, учёные, похоже, обнаружили, что ДНК может действовать примерно так же, как плитки Вана в том смысле, что соединения выполняются только между совместимыми гранями. Благодаря этому сейчас ведутся исследования вычислений на основе ДНК, основанные на процессе вычислений при помощи плиток Вана. Довольно интересная тема!
Вот реализация вычисления простых чисел при помощи плиток Вана в Shadertoy в пиксельном шейдере WebGL:
Shadertoy: WangTiles: PrimeGenerator
Вот ещё несколько отличных видео про машины Тьюринга и проблему остановки:
Turing Machines Explained – Computerphile
Turing & The Halting Problem – Computerphile
А вот ещё несколько ссылок:
Computing With Tiles
Википедия: плитки Вана
Wang Tiles and Turing Machines
Wang Tiles – 1
Вот несколько научных статей:
Computing With Tiles
Computability of Tilings


GlukKazan
Ковры Вана