Привет, Хабр! Привожу тут перевод оригинальной статьи «PRESENT: An Ultra-Lightweight Block Cipher» за авторством Robert B. Weide Богданова, Лендера, Паара, Пошмана, Робшава, Сеурина и Виккелсоя.

После внедрения AES потребность в новых алгоритмах блочного шифрования резко упала, поскольку в большинстве случаев AES является отличным решением. Однако, несмотря на простоту реализации, AES не подходит для сверх ограниченных окружений, типа RFID меток и считывателей. В данной статье будет описан сверх-легкий блочный шифрующий алгоритм PRESENT. Во время разработки этого алгоритма во внимание были приняты как эффективность воплощения в железо, так и надежность шифровки. В итоге результат системных требований сравним с сегодняшними ведущими компактными потоковыми шифрами.
Основной курс в IT текущего столетия — развитие малых вычислительных устройств, причем применяемых не только потребительских товарах, но и формирующих неотъемлемую — и незаметную — часть окружения — инфраструктуру связи. Уже выявлено, что подобные внедрения создают целый спектр весьма конкретных угроз безопасности. В то же время, подручные криптографические решения, даже довольно примитивные, зачастую не подходят для использования в сильно ограниченных по ресурсам окружениях.
В этой статье мы предлагаем новый, оптимизированный по железу блочный алгоритм шифровки, разработанный с условиями максимально возможных ограничений по размерам и энергопотреблению. В то же время, мы попытались избежать компрометации данных. Для достижения этого мы воспользовались опытом DES и дополнили свойствами Serpent, как показавшего восхитительную производительность в железе.
Пожалуй, здесь стоит пояснить, почему мы вообще решили разрабатывать новый блочный шифр, ведь общепризнанный факт заключается в том, что поточные шифры, потенциально, более компактны. Действительно, в начале мы приложили усилия по пониманию устройства компактных поточных шифров в процессе работы над проектом eSTREAM, а так же нескольких других многообещающих предположений, кажущихся быстродейственными. Но мы заметили несколько причин, по которым выбрали все-таки блочный шифр. Во-первых, блочное шифрование универсально и примитивно, а при использовании его в режиме шифрования, т.е. используя уже зашифрованные блоки для шифровки следующих, мы получаем потоковое шифрование. Во-вторых, и, пожалуй, в-главных, тонкости принципов работы блочных шифров кажутся лучше исследованными, нежели чем принципы работы поточных шифрующих алгоритмов. К примеру, в то время как есть обширная теория на базе использования регистров сдвига с линейной обратной связью, не так просто объединить эти блоки так, чтобы получить безопасное предложение. Мы предполагаем, что аккуратно спроектированный блочный шифр может быть более безопасен, нежели чем свежесозданный поточный шифр. Таким образом, получаем, что блочный шифр, требующий столько же ресурсов железа, сколько и компактный поточный шифр, может быть весьма интересен.
Важно отметить, что создавая новый блочный шифрующий алгоритм, особенно с выделяющейся производительностью, мы не просто гонимся за инновациями. Напротив, разработка и реализация шифра идут рука об руку, выявляя некоторые фундаментальные пределы и присущие ограничения. Например, заданный уровень безопасности накладывает ограничения на минимальную длину ключа и блока. Даже обработка 64-битного состояния 80-битным ключом ограничивает минимальный размер устройства. Также можно заметить, что воплощение в «железо» — в особенности же компактность аппаратной реализации — способствует повторяемости. Даже малые изменения могут негативно сказаться на объеме устройства. Однако, криптоаналитики так же ценят повторяемость и ищут математические структуры, которые легко размножаются во многих раундах. Так как много простых повторяющихся структур можно использовать, не подрывая безопасность системы?
Итак, в данной статье будет описан компактный блочный шифр PRESENT. После короткого ревью существующей литературы, всю остальную статью мы оформили в стандартном виде. Шифр описан в секции 3, в секции 4 описаны проектные решения. В 5 секции мы рассмотрим безопасность, тогда как секция 6 будет содержать в себе детальный анализ производительности. Завершается же данный труд нашими выводами.
В то время, как объем работ, посвященных дешевой криптографии непрерывно растет, количество статей посвященных сверх-легким шифрам на удивление мало. Переводя фокус на устройство протокола, мы перестанем ссылаться на работы по дешевым протоколам связи и идентификации. Одна из наиболее обширных работ по компактной реализации в настоящий момент связана с проектом eSTREAM. В рамках одной из частей этого проекта были предложены новые поточные шифры, приспособленные к эффективному воплощению в «железе». По ходу данной работы намечаются многообещающие кандидаты. Пока соотношения примерны, но из брошюр по внедрению следует, что для компактных шифров проекта eSTREAM потребуется порядка 1300-2600 GE (Gate equivalents).
Среди блочных шифров, один из широко известных, а именно DES был создан с учетом эффективности по оборудованию. Помятуя о весьма ограниченном состоянии полупроводников в начале 1970-х, не удивительно, что DES обладает весьма конкурентноспособными свойствами в реализации. Во время разработки, на DES исполнение было затрачено 3000GE, а после сериализации это число опустилось до 2300GE. Однако длина ключа DES ограничивает его полезность во многих приложениях и приводит к тому, что на его основе разрабатываются специализированные модификации, например, с повышенной криптостойкостью или удлиненным ключом.
Касательно современных блочных шифров, в этой статье приводится тщательный анализ дешевого в исполнении AES. Однако, на его реализацию требуется порядка 3600 GE, что является непрямым следствием проектировки штфра под 8- и 32-битные процессоры. Системные требования <a href=" TEA не известны, однако по прикидкам требуют около 2100 GE. Есть и еще 4 решения, заточенных под дешевое оборудование: mCRYPTON (имеет точное исполнение в 2949 GE), HIGHT (около 3000 GE), SEA (порядка 2280 GE) и CGEN (так же около 2280 GE), несмотря на то, что последний и не был задуман как блочный шифр.
PRESENT — частный случай SP-сети и состоит из 31 раунда. Длина блока составляет 64 бита, а ключи поддерживаются в 2 вариантах, 80- и 128-битные. Такого уровня защиты должно вполне хватать для низкозащищенных приложений, обычно используемых для развертывания на основе тегов, а кроме того, что важнее, PRESENT во многом совпадает своими конструтивными особенностями с поточными шифрами проекта eSTREAM, заточенными на эффективную реализацию в железе, что позволяет нам адекватно сравнивать их.
Требования по безопасности и эксплуатационные свойства 128-битных версий предоставлены в приложении к оригинальной статье.
Каждый из 31 раундов состоит из операции XOR, чтобы ввести ключ Ki для 1 ? i ? 32, где K32 используется для «отбеливания» ключа, линейной побитовой перестановки и нелинейного слоя замещения (или, попросту говоря, увеличения стойкости шифрования). Нелинейный слой использует раздельные 4-битные S-блоки, которые применяются параллельно 16 раз на каждом раунде. Шифр, описанный псевдо-кодом представлен на рисунке:

Теперь каждая стадия определяется по очереди. Обоснования конструкции приведены в 4 разделе, а биты всюду нумеруются с нуля, начиная с правого в блоке или слове.
Добавление раундового ключа (addRoundKey). Задан раундовый ключ Ki = ki63… ki0, где 1 ? i ? 32, а так же текущее состояние b63… b0. Добавление раундового ключа к текущему состоянию происходит по модулю 2 (bj = bj ? kij, где 0 ? j ? 63).
Слой S-блоков (sBoxlayer). Используемые в PRESENT S-блоки отображают 4-битные блоки в 4-битные блоки. Действие этого блока в шестнадцатеричной системе счисления приведено в следующей таблице:

Для слоя S-блоков текущее состояние b63… b0 представляет из себя 16 4-битных слов w15… w0, где wi = b4*i+3 || b4*i+2 || b4*i+1 || b4*i для 0 ? i ? 15. Выход рамки S[wi] выдает обновленные значения состояний очевидным образом.
Слой перестановки (pLayer). Побитовая перестановка, используемая в PRESENT задается следующей таблицей (бит i состояния смещается на позицию P(i)):
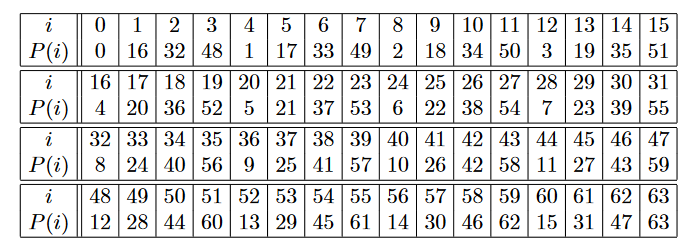
Преобразование ключа (The key schedule). PRESENT может использовать 80- и 128-битные ключи, однако сосредоточимся на 80-битной версии. Предоставляемый пользователем ключ хранится в регистре ключей K, представленный в виде k79k78… k0. На i-ом раунде 64-битный раундовый ключ Ki = k63k62… k0, состоящий из 64 левых битов текущего содержимого регистра K. Таким образом, на i-ом раунде имеем:
Ki = k63k62… k0 = k79k78… k16.
После распаковки раундового ключа Ki регистр ключа K = k79k78… k0 обновляется следующим образом:
1. [k79k78… k1k0] = [k18k17… k20k19]
2. [k79k78k77k76] = S[k79k78k77k76]
3. [k19k18k17k16k15] = [k19k18k17k16k15] ? round_counter
Следовательно, регистр ключа сдвигается на 61 позицию влево, 4 крайних левых бита, прошедших через S-блок и round_counter значение i складывается по модулю 2 с битами k19k18k17k16k15 из K с наименьшим значащим битом из round_counter справа.

Преобразование ключа для 128-битного алгоритма можно найти в приложении к оригинальной статье.
Помимо безопасности и эффективной реализации, основное достижение PRESENT — его простота. по этому не удивительно, что похожие проекты были приняты в других обстоятельствах, и даже были использованы как учебное пособие для студентов. В данной секции мы обоснуем решения, принятые нами при проектировке PRESENT. Однако, в первую очередь, опишем ожидаемые прикладные требования.
При проектировке блочного шифра, применимого в жестко ограниченных окружениях, важно понять, что мы не создаем блочный шифр, который, непременно, будет применим во многих ситуациях — для этого существует AES. Наоборот, мы нацелены на весьма специфичное применение, для которого AES не подходит. Вышесказанное предопределяет нам следующие характеристики.
Исходя из таких соображений, мы решили создать PRESENT как 64-битный блочный шифр с 80-битным ключом. Шифровка и дешифровка, в данном случае, имеют примерно схожие физические требования. Имея возможность поддерживать как шифрацию, так и дешифрацию, PRESENT будет компактнее, чем поддерживающий лишь шифрацию AES. А в случае encryption-only исполнения, наш шифр окажется и вовсе сверх-легким. Шифрующие суб-ключи будут вычисляться на ходу.
В литературе есть множество примеров атак компромисса между временем, датой и памятью, или атак с использованием парадокса дней рождения при шифровке больших объемов данных. Однако, данные атаки зависят только от параметров шифра и не используют внутреннюю структуру. Наша цель состоит в том, чтобы эти атаки были лучшим, что могут применить против нас. Атаки стороннего канала и атаки с непосредственным взломом чипа угрожают PRESENT в той же мере, как и прочим криптографическим примитивам. Однако для вероятных применений, умеренные требования безопасности делают выгоду, получаемую злоумышленником на практике, весьма ограниченной. В оценке рисков, подобные угрозы не воспринимаются как существенный фактор.
При выборе слоя смешивания ключа, наше внимание к аппаратной эффективности требует наличия линейного слоя, который может быть реализован с минимальным количеством управляющих элементов (например, транзисторов). это приводит к побитовой перестановке. Уделяя внимание простоте, мы выбрали регулярную битовую перестановку, что помогает провести прозрачный анализ безопасности(см. 5 раздел).
В PRESENT мы используем раздельные S-блоки, переводящие 4 бита в 4 бита (F42>F42). Это прямое следствие нашего стремления к аппаратной эффективности, при этом реализация такого S-блока обычно намного компактнее, чем у 8-битного S-блока. Поскольку мы используем битовую перестановку для линейного диффузионного слоя, AES-подобные диффузионные технологии не являются вариантом для нашего шифра. Поэтому мы помещаем некоторые дополнительные условия на S-блоки, чтобы уменьшить так называемый «лавинный эффект». Точнее, S-блоки для PRESENT удовлетворяют следующим условиям, где мы обозначим коэффициент Фурье S через
SWb(a) = ?(-1)<b, S(x)>+<a,x>, x?F42
1. Для любого фиксированного ненулевого входного смещения ?I ? F42 и любого фиксированного ненулевого входного смещения ?O ? F42 внутри S-блока требуем
#{x ? F42|S(x) + S(x+?I) = ?O} ? 4.
2. Для любой фиксированной ненулевой входной разнице ?I ? F42 и любой фиксированной ненулевой выходной разнице ?O ? F42, такой что wt(?I) = wt(?O) = 1, имеем
{x ? F42|S(x) + S(x+?I) = ?O} = ?
3. Для всех ненулевых a ? F42 и всех ненулевых b ? F4 выполняется что |SWb(a)| ? 8
4. Для всех ненулевых a ? F42 и всех ненулевых b ? F4, таких что wt(a) = wt(b) = 1 выполняется SWb(a) = ± 4
Как станет ясно из секции 5, эти условия гарантируют, что PRESENT устойчив к дифференциальным и линейным атакам. Используя классификацию всех 4-битных S-блоков, удовлетворяющих вышеприведенным условиям, мы выбрали S-блок, который особенно хорошо подходит для эффективной аппаратной реализации.
А теперь мы представим результаты анализа безопасности PRESENT.
Дифференциальный и линейный криптоанализ являются одними из самых мощных методов, доступных криптоаналитику. Чтобы измерить сопротивление PRESENT дифференциальному и линейному криптоанализу, мы задаем нижнюю границу числа так называемых активных S-блоков, участвующих в дифференциальной (или линейной) характеристике.
Случай дифференциального криптоанализа охвачен следующей теоремой.
Теорема 1. Любая пятиконтурная дифференциальная характеристика PRESENT имеет минимум 10 активных S-блоков.
Теорема 1 доказывается в 3 приложении оригинальной статьи, а мы продолжим наблюдения. Разделим 16 S-блоков в 4 группы:
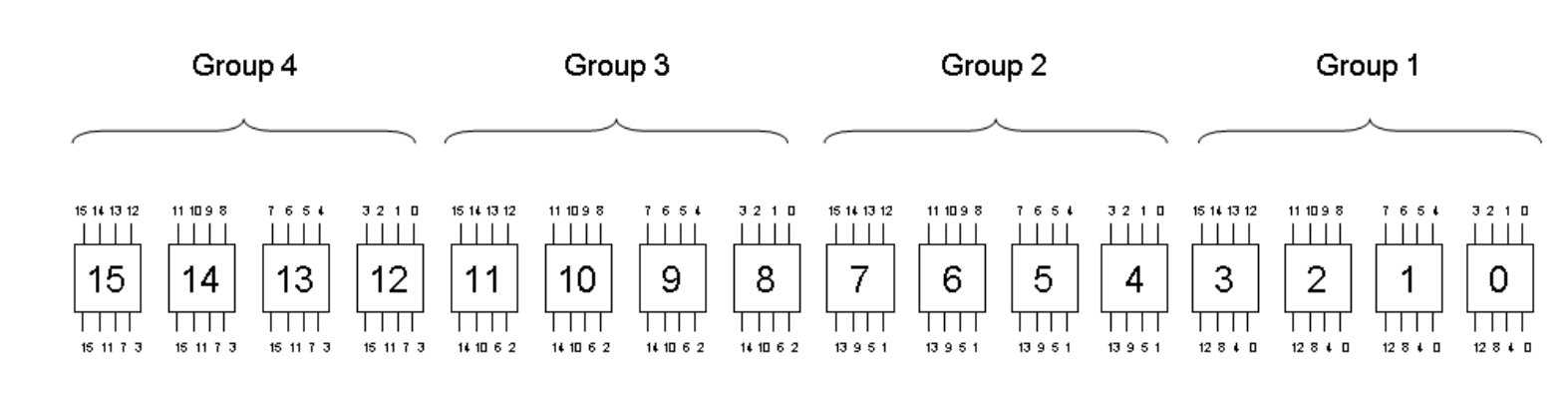
Числа на входе (сверху) обозначают номер S-блока на предыдущем шаге, а на выходе (снизу) — на последующем
Заметим, что:
Согласно теореме 1, любая дифференциальная характеристика за более чем 25 раундов PRESENT должна иметь не менее 5?10 = 50 активных S-блоков. Максимальная дифференциальная вероятность S-блока PRESENT равна 2-2, и поэтому вероятность единственной 25-раундовой дифференциальной характеристики ограничена 2-100. Продвинутые методы позволяют криптоаналитику удалить внешние раунды из шифра, чтобы использовать более короткую характеристику.Однако даже если мы позволим злоумышленнику удалить шесть раундов из шифра, что является беспрецедентной ситуацией, то данные, необходимые для использования оставшейся 25-раундовой дифференциальной характеристики, превысят доступное количество. Таким образом, границы безопасности более, чем надежные. Однако мы практически подтвердили, что граница числа активных S-блоков в Теореме 1 является жесткой.
Мы можем определить характеристики, которые включают в себя десять S-блоков в течение пяти раундов. Следующая двухраундовая итерационная характеристика включает в себя два S-блока за раунд и держится с вероятностью 2?25 за пять раундов.
Более сложные характеристики держатся с вероятностью 2-21 на протяжении 5 раундов.
Хотя вероятность этой второй характеристики очень близка к границе 2-20, она не является итерационной и имеет мало практической ценности. Вместо этого мы экспериментально подтвердили вероятность двухраундового итерационного дифференциала. В экспериментах с более чем 100 независимыми суб-ключами, использующими 223 выбранных пары открытого текста, наблюдаемая вероятность была предсказана. Это, по-видимому, предполагает, что для этой конкретной характеристики не существует сопутствующего значащего дифференциала. Однако определение степени любого дифференциального эффекта является сложной и трудоемкой задачей, даже несмотря на то, что наш предварительный анализ был обнадеживающим.
Случай линейного криптоанализа PRESENT рассматривается следующей теоремой, в которой мы анализируем наилучшее линейное приближение к четырем раундам PRESENT.
Теорема 2. Обозначим E4R — максимальное смещение линейного приближения четырех раундов использования PRESENT. Тогда E4R ? 2-7.
Доказательство теоремы содержится в в приложении 4 оригинальной статьи. Тогда для 28 раундов максимальное смещение составит
26 ? E4R7 = 26 ? (2-7)7 = 2-43
Поэтому в предположении, что криптоаналитику нужно только приблизительно 28 из 31 раунда в PRESENT, чтобы инициировать атаку восстановления ключа, линейный криптоанализ шифра потребует порядка 284 известных открытых текстов / шифротекстов. Такие требования к данным превышают доступный текст.
Структура PRESENT позволяет нам рассмотреть некоторые выделенные формы атак. Однако ни одна из них не привела к атаке, требующей меньше текста, чем нижняя граница требований к тексту для линейного криптоанализа. Среди выделенных атак мы рассматривали одну, использующую палиндромные различия, так как симметричные различия сохраняются с вероятностью один (т.е. всегда) над диффузионным слоем, и некоторые продвинутые варианты дифференциально-линейных атак. Хотя атаки казались многообещающими в течение нескольких раундов, они очень быстро потеряли свою практическую ценность и вряд ли будут полезны в криптоанализе PRESENT. Мы также установили, что усеченный дифференциальный криптоанализ, вероятно, будет иметь ограниченное значение, хотя следующие два раунда.
Усеченное расширение выполняется с вероятностью один.
Даже при использовании для уменьшения длины уже идентифицированных дифференциальных характеристик требования к данным остаются чрезмерными. Ранкированное расширение выполняется с вероятностью один.
Структурные атаки, такие как интегральный криптоанализ и анализ бутылочного горлышка, хорошо подходят для анализа AES-подобных шифров. Такие шифры имеют сильные словоподобные структуры, где слова обычно являются байтами.Однако конструкция представления почти исключительно побитовая, и хотя операция перестановки несколько регулярна, развитие и распространение словесных структур нарушаются побитовыми операциями, используемыми в шифре.
Алгебраические атаки имели больший успех, когда применялись к потоковым шифрам, чем к блочным. Тем не менее, простая структура PRESENT означает, что они заслуживают серьезного изучения. S-блок PRESENT описывается 21 квадратичным уравнением для восьми входных / выходных битовых переменных над полем G(2). Это неудивительно, поскольку хорошо известно, что любой четырехбитный S-блок может быть описан по крайней мере 21 таким уравнением. Затем весь шифр может быть описан квадратными уравнениями e=n?21 в переменных v=n?8, где n-число S-блоков в алгоритме шифрования и преобразования ключей.
Для PRESENT мы имеем n = (31?16) + 31 таким образом, вся система состоит из 11 067 квадратных уравнений в 4 216 переменных.Общая задача решения системы многомерных квадратных уравнений является NP-трудной. Однако системы, полученные для блочных шифров, очень редки, так как они состоят из n небольших систем, Соединенных простыми линейными слоями. Тем не менее, неясно, можно ли использовать этот факт в так называемой алгебраической атаке. Были предложены некоторые специализированные методы, такие как XL и XSL, хотя были обнаружены недостатки в обоих методах. Вместо этого единственные практические результаты по алгебраическому криптоанализу блочных шифров были получены путем применения алгоритмов Бухбергера и F4 в рамках Magma. Моделирование на маломасштабных версиях AES показало, что для всех, кроме самых маленьких SP-сетей, быстро возникают трудности как во времени, так и в сложности памяти. То же самое относится и к PRESENT.
Практическое подтверждение. Мы провели моделирование на мелкомасштабных версиях, используя алгоритм F4 в Magma. Когда есть один S-блок, то есть очень маленький блок размером в четыре бита, то Magma может решить полученную систему уравнений за много раундов. Однако при увеличении размера блока и добавлении S-блоков, наряду с соответствующим вариантом линейного диффузионного слоя, система уравнений вскоре становится слишком большой. Даже при рассмотрении системы, состоящей из семи S-блоков, т. е. имея размер блока 28 бит, мы не смогли в разумные сроки получить решение для прошедшего два раунда варианта сокращенного шифра. Наш анализ показывает, что алгебраические атаки вряд ли представляют угрозу для PRESENT.
Поскольку не существует никаких установленных руководящих принципов для разработки преобразований ключа, существует как большое разнообразие проектов, так и большое разнообразие атак, исходя из особенностей проекта. Наиболее эффективные атаки подпадают под общую рубрику атака на связанных ключах и сдвиговая атака, и обе основаны на построении идентифицируемых соотношений между различными наборами суб-ключей. Чтобы противостоять этой угрозе, мы используем раунд-зависимый счетчик, так что наборы суб-ключей не могут быть легко «сдвинуты», и мы используем нелинейную операцию для смешивания содержимого ключевого регистра K. В частности:
Мы считаем, что этих свойств достаточно, чтобы противостоять ключевым атакам на основе преобразования ключа.
Мы реализовали PRESENT-80 в VHDL и адаптировали его для стандартной библиотеки ячеек Virtual Silicon (VST) на основе UMC L180 0.18 ? 1P6M Logic. Мы использовали Mentor Graphics Modelsim SE PLUS 5.8 c для моделирования и Synopsys Design Compilerversion Y-2006.06 для синтеза и моделирования мощности потребления. Были использованы типичные для литейного производства значения (1,8 Вольта для напряжения сердечника и 25°C для температуры), а для моделирования мощности применена предложенная модель проволочной нагрузки. Обратите внимание, что подобное моделирование преназначено для конструкций около 10 000 GE, поэтому результаты мощности будут пессимистичными для значительно меньших конструкций. На рисунке

показан путь данных оптимизированного по пространству PRESENT-80 без возможности дешифровки (encryption-only), который выполняет один раунд за один такт, т. е. путь данных 64-разрядной ширины. Обратите внимание, что на этапе проектирования PRESENT мы используем один и тот же S-блок 16 раз вместо того, чтобы иметь 16 различных S-блоков, и это облегчает дальнейшую сериализацию проекта, т. е. с 4-битным каналом передачи данных. Наша реализация требует 32 тактовых цикла для шифрования 64-битного открытого текста с 80-битным ключом, занимает 1570 GE и имеет в модуляции энергопотребление 5 мкВт.

Пространственные требования PRESENT
Большую часть площади занимают триггеры для хранения ключа и состояния данных, за которыми следуют S-слой и отдел XOR'ирования ключа. Битовые перестановки простой проводки увеличат площадь только тогда, когда реализация дойдет до этапа place&route. Заметим, что основной целью нашей реализации был небольшой объем аппаратного обеспечения, однако мы также синтезировали оптимизированный по мощности процесс. Для дополнительных 53 GE мы достигаем энергопотребления всего 3,3 мкВт, а нынешний-128 будет занимать оценочную площадь 1886 GE. Помимо очень малого размера PRESENT имеет довольно высокую пропускную способность, дающую хорошую энергию на бит. Сравнение с другими шифрами приведено в таблице:

В этой статье мы описали новый блочный шифр PRESENT. Нашей целью был сверхлегкий шифр, который обеспечивает уровень безопасности, соизмеримый с размером 64-битного блока и 80-битным ключом. В итоге, PRESENT имеет требования к реализации, аналогичные многим компактным потоковым шифрам. Поэтому мы считаем, что он представляет как теоретический, так и практический интерес. Как и все новые предложения, мы не поощряем немедленное развертывание PRESENT, но настоятельно призываем к его анализу.
Работа, представленная в настоящем документе, была частично поддержана Европейской комиссией в рамках STREP UbiSec&Sens of the EU Framework Programme 6for Research and Development (www.ist-ubisecsens.org). Мнения и выводы, содержащиеся в настоящем документе, принадлежат авторам и не должны интерпретироваться как представляющие собой официальную политику или одобрение, выраженное или подтвержденное проектом UbiSec&Sens или Европейской комиссией.

Аннотация
После внедрения AES потребность в новых алгоритмах блочного шифрования резко упала, поскольку в большинстве случаев AES является отличным решением. Однако, несмотря на простоту реализации, AES не подходит для сверх ограниченных окружений, типа RFID меток и считывателей. В данной статье будет описан сверх-легкий блочный шифрующий алгоритм PRESENT. Во время разработки этого алгоритма во внимание были приняты как эффективность воплощения в железо, так и надежность шифровки. В итоге результат системных требований сравним с сегодняшними ведущими компактными потоковыми шифрами.
1. Введение
Основной курс в IT текущего столетия — развитие малых вычислительных устройств, причем применяемых не только потребительских товарах, но и формирующих неотъемлемую — и незаметную — часть окружения — инфраструктуру связи. Уже выявлено, что подобные внедрения создают целый спектр весьма конкретных угроз безопасности. В то же время, подручные криптографические решения, даже довольно примитивные, зачастую не подходят для использования в сильно ограниченных по ресурсам окружениях.
В этой статье мы предлагаем новый, оптимизированный по железу блочный алгоритм шифровки, разработанный с условиями максимально возможных ограничений по размерам и энергопотреблению. В то же время, мы попытались избежать компрометации данных. Для достижения этого мы воспользовались опытом DES и дополнили свойствами Serpent, как показавшего восхитительную производительность в железе.
Пожалуй, здесь стоит пояснить, почему мы вообще решили разрабатывать новый блочный шифр, ведь общепризнанный факт заключается в том, что поточные шифры, потенциально, более компактны. Действительно, в начале мы приложили усилия по пониманию устройства компактных поточных шифров в процессе работы над проектом eSTREAM, а так же нескольких других многообещающих предположений, кажущихся быстродейственными. Но мы заметили несколько причин, по которым выбрали все-таки блочный шифр. Во-первых, блочное шифрование универсально и примитивно, а при использовании его в режиме шифрования, т.е. используя уже зашифрованные блоки для шифровки следующих, мы получаем потоковое шифрование. Во-вторых, и, пожалуй, в-главных, тонкости принципов работы блочных шифров кажутся лучше исследованными, нежели чем принципы работы поточных шифрующих алгоритмов. К примеру, в то время как есть обширная теория на базе использования регистров сдвига с линейной обратной связью, не так просто объединить эти блоки так, чтобы получить безопасное предложение. Мы предполагаем, что аккуратно спроектированный блочный шифр может быть более безопасен, нежели чем свежесозданный поточный шифр. Таким образом, получаем, что блочный шифр, требующий столько же ресурсов железа, сколько и компактный поточный шифр, может быть весьма интересен.
Важно отметить, что создавая новый блочный шифрующий алгоритм, особенно с выделяющейся производительностью, мы не просто гонимся за инновациями. Напротив, разработка и реализация шифра идут рука об руку, выявляя некоторые фундаментальные пределы и присущие ограничения. Например, заданный уровень безопасности накладывает ограничения на минимальную длину ключа и блока. Даже обработка 64-битного состояния 80-битным ключом ограничивает минимальный размер устройства. Также можно заметить, что воплощение в «железо» — в особенности же компактность аппаратной реализации — способствует повторяемости. Даже малые изменения могут негативно сказаться на объеме устройства. Однако, криптоаналитики так же ценят повторяемость и ищут математические структуры, которые легко размножаются во многих раундах. Так как много простых повторяющихся структур можно использовать, не подрывая безопасность системы?
Итак, в данной статье будет описан компактный блочный шифр PRESENT. После короткого ревью существующей литературы, всю остальную статью мы оформили в стандартном виде. Шифр описан в секции 3, в секции 4 описаны проектные решения. В 5 секции мы рассмотрим безопасность, тогда как секция 6 будет содержать в себе детальный анализ производительности. Завершается же данный труд нашими выводами.
2. Существующие труды
В то время, как объем работ, посвященных дешевой криптографии непрерывно растет, количество статей посвященных сверх-легким шифрам на удивление мало. Переводя фокус на устройство протокола, мы перестанем ссылаться на работы по дешевым протоколам связи и идентификации. Одна из наиболее обширных работ по компактной реализации в настоящий момент связана с проектом eSTREAM. В рамках одной из частей этого проекта были предложены новые поточные шифры, приспособленные к эффективному воплощению в «железе». По ходу данной работы намечаются многообещающие кандидаты. Пока соотношения примерны, но из брошюр по внедрению следует, что для компактных шифров проекта eSTREAM потребуется порядка 1300-2600 GE (Gate equivalents).
Среди блочных шифров, один из широко известных, а именно DES был создан с учетом эффективности по оборудованию. Помятуя о весьма ограниченном состоянии полупроводников в начале 1970-х, не удивительно, что DES обладает весьма конкурентноспособными свойствами в реализации. Во время разработки, на DES исполнение было затрачено 3000GE, а после сериализации это число опустилось до 2300GE. Однако длина ключа DES ограничивает его полезность во многих приложениях и приводит к тому, что на его основе разрабатываются специализированные модификации, например, с повышенной криптостойкостью или удлиненным ключом.
Касательно современных блочных шифров, в этой статье приводится тщательный анализ дешевого в исполнении AES. Однако, на его реализацию требуется порядка 3600 GE, что является непрямым следствием проектировки штфра под 8- и 32-битные процессоры. Системные требования <a href=" TEA не известны, однако по прикидкам требуют около 2100 GE. Есть и еще 4 решения, заточенных под дешевое оборудование: mCRYPTON (имеет точное исполнение в 2949 GE), HIGHT (около 3000 GE), SEA (порядка 2280 GE) и CGEN (так же около 2280 GE), несмотря на то, что последний и не был задуман как блочный шифр.
3. Блочный шифр PRESENT
PRESENT — частный случай SP-сети и состоит из 31 раунда. Длина блока составляет 64 бита, а ключи поддерживаются в 2 вариантах, 80- и 128-битные. Такого уровня защиты должно вполне хватать для низкозащищенных приложений, обычно используемых для развертывания на основе тегов, а кроме того, что важнее, PRESENT во многом совпадает своими конструтивными особенностями с поточными шифрами проекта eSTREAM, заточенными на эффективную реализацию в железе, что позволяет нам адекватно сравнивать их.
Требования по безопасности и эксплуатационные свойства 128-битных версий предоставлены в приложении к оригинальной статье.
Каждый из 31 раундов состоит из операции XOR, чтобы ввести ключ Ki для 1 ? i ? 32, где K32 используется для «отбеливания» ключа, линейной побитовой перестановки и нелинейного слоя замещения (или, попросту говоря, увеличения стойкости шифрования). Нелинейный слой использует раздельные 4-битные S-блоки, которые применяются параллельно 16 раз на каждом раунде. Шифр, описанный псевдо-кодом представлен на рисунке:

Теперь каждая стадия определяется по очереди. Обоснования конструкции приведены в 4 разделе, а биты всюду нумеруются с нуля, начиная с правого в блоке или слове.
Добавление раундового ключа (addRoundKey). Задан раундовый ключ Ki = ki63… ki0, где 1 ? i ? 32, а так же текущее состояние b63… b0. Добавление раундового ключа к текущему состоянию происходит по модулю 2 (bj = bj ? kij, где 0 ? j ? 63).
Слой S-блоков (sBoxlayer). Используемые в PRESENT S-блоки отображают 4-битные блоки в 4-битные блоки. Действие этого блока в шестнадцатеричной системе счисления приведено в следующей таблице:

Для слоя S-блоков текущее состояние b63… b0 представляет из себя 16 4-битных слов w15… w0, где wi = b4*i+3 || b4*i+2 || b4*i+1 || b4*i для 0 ? i ? 15. Выход рамки S[wi] выдает обновленные значения состояний очевидным образом.
Слой перестановки (pLayer). Побитовая перестановка, используемая в PRESENT задается следующей таблицей (бит i состояния смещается на позицию P(i)):

Преобразование ключа (The key schedule). PRESENT может использовать 80- и 128-битные ключи, однако сосредоточимся на 80-битной версии. Предоставляемый пользователем ключ хранится в регистре ключей K, представленный в виде k79k78… k0. На i-ом раунде 64-битный раундовый ключ Ki = k63k62… k0, состоящий из 64 левых битов текущего содержимого регистра K. Таким образом, на i-ом раунде имеем:
Ki = k63k62… k0 = k79k78… k16.
После распаковки раундового ключа Ki регистр ключа K = k79k78… k0 обновляется следующим образом:
1. [k79k78… k1k0] = [k18k17… k20k19]
2. [k79k78k77k76] = S[k79k78k77k76]
3. [k19k18k17k16k15] = [k19k18k17k16k15] ? round_counter
Следовательно, регистр ключа сдвигается на 61 позицию влево, 4 крайних левых бита, прошедших через S-блок и round_counter значение i складывается по модулю 2 с битами k19k18k17k16k15 из K с наименьшим значащим битом из round_counter справа.

Преобразование ключа для 128-битного алгоритма можно найти в приложении к оригинальной статье.
4. Конструктивные особенности PRESENT
Помимо безопасности и эффективной реализации, основное достижение PRESENT — его простота. по этому не удивительно, что похожие проекты были приняты в других обстоятельствах, и даже были использованы как учебное пособие для студентов. В данной секции мы обоснуем решения, принятые нами при проектировке PRESENT. Однако, в первую очередь, опишем ожидаемые прикладные требования.
4.1. Цели и среда применения
При проектировке блочного шифра, применимого в жестко ограниченных окружениях, важно понять, что мы не создаем блочный шифр, который, непременно, будет применим во многих ситуациях — для этого существует AES. Наоборот, мы нацелены на весьма специфичное применение, для которого AES не подходит. Вышесказанное предопределяет нам следующие характеристики.
- Шифр будет реализован «в железе»
- Приложения будут требоваться лишь для регулировки уровня безопасности. Следовательно, 80-битный ключ будет здравым решением. Отметим, что такой же позиции придерживаются разработчики потоковых шифров проекта eSTREAM.
- Приложения не предполагают шифровки большого количества данных. Таким образом, реализация может быть оптимизирована для производительности или пространства без внесения слишком больших изменений.
- В некоторых применениях возможна ситуация, что ключ будет зафиксирован при производстве. В таком случае, не надо будет изменять ключ устройства (что может вылиться в атаки с манипуляцией ключом).
- Физический объем устройства будет первым приоритетом, после безопасности, что повлечет ограничения на пиковые и средние потребления энергии, и, следовательно, сдвинет быстродействие в область низкоприоритетных параметров.
- В устройствах, требующих наиболее эффективного использования физического пространства, блочный шифр зачастую сможет лишь шифровать данные (encryption-only mode). Таким образом, он сможет быть использован в запрос-ответ (challenge-response) протоколах авторизации, и, при соблюдении контроля состояния, может быть использован для шифровки и дешифровки переговоров с устройством, используя режим счетчика.
Исходя из таких соображений, мы решили создать PRESENT как 64-битный блочный шифр с 80-битным ключом. Шифровка и дешифровка, в данном случае, имеют примерно схожие физические требования. Имея возможность поддерживать как шифрацию, так и дешифрацию, PRESENT будет компактнее, чем поддерживающий лишь шифрацию AES. А в случае encryption-only исполнения, наш шифр окажется и вовсе сверх-легким. Шифрующие суб-ключи будут вычисляться на ходу.
В литературе есть множество примеров атак компромисса между временем, датой и памятью, или атак с использованием парадокса дней рождения при шифровке больших объемов данных. Однако, данные атаки зависят только от параметров шифра и не используют внутреннюю структуру. Наша цель состоит в том, чтобы эти атаки были лучшим, что могут применить против нас. Атаки стороннего канала и атаки с непосредственным взломом чипа угрожают PRESENT в той же мере, как и прочим криптографическим примитивам. Однако для вероятных применений, умеренные требования безопасности делают выгоду, получаемую злоумышленником на практике, весьма ограниченной. В оценке рисков, подобные угрозы не воспринимаются как существенный фактор.
4.2. Перестановочный слой
При выборе слоя смешивания ключа, наше внимание к аппаратной эффективности требует наличия линейного слоя, который может быть реализован с минимальным количеством управляющих элементов (например, транзисторов). это приводит к побитовой перестановке. Уделяя внимание простоте, мы выбрали регулярную битовую перестановку, что помогает провести прозрачный анализ безопасности(см. 5 раздел).
4.3. S-блоки.
В PRESENT мы используем раздельные S-блоки, переводящие 4 бита в 4 бита (F42>F42). Это прямое следствие нашего стремления к аппаратной эффективности, при этом реализация такого S-блока обычно намного компактнее, чем у 8-битного S-блока. Поскольку мы используем битовую перестановку для линейного диффузионного слоя, AES-подобные диффузионные технологии не являются вариантом для нашего шифра. Поэтому мы помещаем некоторые дополнительные условия на S-блоки, чтобы уменьшить так называемый «лавинный эффект». Точнее, S-блоки для PRESENT удовлетворяют следующим условиям, где мы обозначим коэффициент Фурье S через
SWb(a) = ?(-1)<b, S(x)>+<a,x>, x?F42
1. Для любого фиксированного ненулевого входного смещения ?I ? F42 и любого фиксированного ненулевого входного смещения ?O ? F42 внутри S-блока требуем
#{x ? F42|S(x) + S(x+?I) = ?O} ? 4.
2. Для любой фиксированной ненулевой входной разнице ?I ? F42 и любой фиксированной ненулевой выходной разнице ?O ? F42, такой что wt(?I) = wt(?O) = 1, имеем
{x ? F42|S(x) + S(x+?I) = ?O} = ?
3. Для всех ненулевых a ? F42 и всех ненулевых b ? F4 выполняется что |SWb(a)| ? 8
4. Для всех ненулевых a ? F42 и всех ненулевых b ? F4, таких что wt(a) = wt(b) = 1 выполняется SWb(a) = ± 4
Как станет ясно из секции 5, эти условия гарантируют, что PRESENT устойчив к дифференциальным и линейным атакам. Используя классификацию всех 4-битных S-блоков, удовлетворяющих вышеприведенным условиям, мы выбрали S-блок, который особенно хорошо подходит для эффективной аппаратной реализации.
5. Анализ безопасности
А теперь мы представим результаты анализа безопасности PRESENT.
Дифференциальный и линейный криптоанализ
Дифференциальный и линейный криптоанализ являются одними из самых мощных методов, доступных криптоаналитику. Чтобы измерить сопротивление PRESENT дифференциальному и линейному криптоанализу, мы задаем нижнюю границу числа так называемых активных S-блоков, участвующих в дифференциальной (или линейной) характеристике.
Дифференциальный криптоанализ
Случай дифференциального криптоанализа охвачен следующей теоремой.
Теорема 1. Любая пятиконтурная дифференциальная характеристика PRESENT имеет минимум 10 активных S-блоков.
Теорема 1 доказывается в 3 приложении оригинальной статьи, а мы продолжим наблюдения. Разделим 16 S-блоков в 4 группы:

Числа на входе (сверху) обозначают номер S-блока на предыдущем шаге, а на выходе (снизу) — на последующем
Заметим, что:
- Входные биты к S-блоку поступают от 4 различных S-блоков одной и той же группы.
- Входные биты на группы из четырех s-блоков приходят из 16 различных s-блоков.
- Четыре выходных бита из конкретного S-блока входят в четыре различных S-блока, каждый из которых принадлежит отдельной группе S-блоков в следующем раунде.
- Выходные биты s-блоков в разных группах идут в различные s-блоки.
Согласно теореме 1, любая дифференциальная характеристика за более чем 25 раундов PRESENT должна иметь не менее 5?10 = 50 активных S-блоков. Максимальная дифференциальная вероятность S-блока PRESENT равна 2-2, и поэтому вероятность единственной 25-раундовой дифференциальной характеристики ограничена 2-100. Продвинутые методы позволяют криптоаналитику удалить внешние раунды из шифра, чтобы использовать более короткую характеристику.Однако даже если мы позволим злоумышленнику удалить шесть раундов из шифра, что является беспрецедентной ситуацией, то данные, необходимые для использования оставшейся 25-раундовой дифференциальной характеристики, превысят доступное количество. Таким образом, границы безопасности более, чем надежные. Однако мы практически подтвердили, что граница числа активных S-блоков в Теореме 1 является жесткой.
Практическое подтверждение
Мы можем определить характеристики, которые включают в себя десять S-блоков в течение пяти раундов. Следующая двухраундовая итерационная характеристика включает в себя два S-блока за раунд и держится с вероятностью 2?25 за пять раундов.
Более сложные характеристики держатся с вероятностью 2-21 на протяжении 5 раундов.
Хотя вероятность этой второй характеристики очень близка к границе 2-20, она не является итерационной и имеет мало практической ценности. Вместо этого мы экспериментально подтвердили вероятность двухраундового итерационного дифференциала. В экспериментах с более чем 100 независимыми суб-ключами, использующими 223 выбранных пары открытого текста, наблюдаемая вероятность была предсказана. Это, по-видимому, предполагает, что для этой конкретной характеристики не существует сопутствующего значащего дифференциала. Однако определение степени любого дифференциального эффекта является сложной и трудоемкой задачей, даже несмотря на то, что наш предварительный анализ был обнадеживающим.
Линейный криптоанализ
Случай линейного криптоанализа PRESENT рассматривается следующей теоремой, в которой мы анализируем наилучшее линейное приближение к четырем раундам PRESENT.
Теорема 2. Обозначим E4R — максимальное смещение линейного приближения четырех раундов использования PRESENT. Тогда E4R ? 2-7.
Доказательство теоремы содержится в в приложении 4 оригинальной статьи. Тогда для 28 раундов максимальное смещение составит
26 ? E4R7 = 26 ? (2-7)7 = 2-43
Поэтому в предположении, что криптоаналитику нужно только приблизительно 28 из 31 раунда в PRESENT, чтобы инициировать атаку восстановления ключа, линейный криптоанализ шифра потребует порядка 284 известных открытых текстов / шифротекстов. Такие требования к данным превышают доступный текст.
Некоторые продвинутые дифференциальные / линейные атаки
Структура PRESENT позволяет нам рассмотреть некоторые выделенные формы атак. Однако ни одна из них не привела к атаке, требующей меньше текста, чем нижняя граница требований к тексту для линейного криптоанализа. Среди выделенных атак мы рассматривали одну, использующую палиндромные различия, так как симметричные различия сохраняются с вероятностью один (т.е. всегда) над диффузионным слоем, и некоторые продвинутые варианты дифференциально-линейных атак. Хотя атаки казались многообещающими в течение нескольких раундов, они очень быстро потеряли свою практическую ценность и вряд ли будут полезны в криптоанализе PRESENT. Мы также установили, что усеченный дифференциальный криптоанализ, вероятно, будет иметь ограниченное значение, хотя следующие два раунда.
Усеченное расширение выполняется с вероятностью один.
Даже при использовании для уменьшения длины уже идентифицированных дифференциальных характеристик требования к данным остаются чрезмерными. Ранкированное расширение выполняется с вероятностью один.
5.2. Структурные атаки
Структурные атаки, такие как интегральный криптоанализ и анализ бутылочного горлышка, хорошо подходят для анализа AES-подобных шифров. Такие шифры имеют сильные словоподобные структуры, где слова обычно являются байтами.Однако конструкция представления почти исключительно побитовая, и хотя операция перестановки несколько регулярна, развитие и распространение словесных структур нарушаются побитовыми операциями, используемыми в шифре.
5.3. Алгебраические атаки
Алгебраические атаки имели больший успех, когда применялись к потоковым шифрам, чем к блочным. Тем не менее, простая структура PRESENT означает, что они заслуживают серьезного изучения. S-блок PRESENT описывается 21 квадратичным уравнением для восьми входных / выходных битовых переменных над полем G(2). Это неудивительно, поскольку хорошо известно, что любой четырехбитный S-блок может быть описан по крайней мере 21 таким уравнением. Затем весь шифр может быть описан квадратными уравнениями e=n?21 в переменных v=n?8, где n-число S-блоков в алгоритме шифрования и преобразования ключей.
Для PRESENT мы имеем n = (31?16) + 31 таким образом, вся система состоит из 11 067 квадратных уравнений в 4 216 переменных.Общая задача решения системы многомерных квадратных уравнений является NP-трудной. Однако системы, полученные для блочных шифров, очень редки, так как они состоят из n небольших систем, Соединенных простыми линейными слоями. Тем не менее, неясно, можно ли использовать этот факт в так называемой алгебраической атаке. Были предложены некоторые специализированные методы, такие как XL и XSL, хотя были обнаружены недостатки в обоих методах. Вместо этого единственные практические результаты по алгебраическому криптоанализу блочных шифров были получены путем применения алгоритмов Бухбергера и F4 в рамках Magma. Моделирование на маломасштабных версиях AES показало, что для всех, кроме самых маленьких SP-сетей, быстро возникают трудности как во времени, так и в сложности памяти. То же самое относится и к PRESENT.
Практическое подтверждение. Мы провели моделирование на мелкомасштабных версиях, используя алгоритм F4 в Magma. Когда есть один S-блок, то есть очень маленький блок размером в четыре бита, то Magma может решить полученную систему уравнений за много раундов. Однако при увеличении размера блока и добавлении S-блоков, наряду с соответствующим вариантом линейного диффузионного слоя, система уравнений вскоре становится слишком большой. Даже при рассмотрении системы, состоящей из семи S-блоков, т. е. имея размер блока 28 бит, мы не смогли в разумные сроки получить решение для прошедшего два раунда варианта сокращенного шифра. Наш анализ показывает, что алгебраические атаки вряд ли представляют угрозу для PRESENT.
5.4. Атаки с преобразованием ключа
Поскольку не существует никаких установленных руководящих принципов для разработки преобразований ключа, существует как большое разнообразие проектов, так и большое разнообразие атак, исходя из особенностей проекта. Наиболее эффективные атаки подпадают под общую рубрику атака на связанных ключах и сдвиговая атака, и обе основаны на построении идентифицируемых соотношений между различными наборами суб-ключей. Чтобы противостоять этой угрозе, мы используем раунд-зависимый счетчик, так что наборы суб-ключей не могут быть легко «сдвинуты», и мы используем нелинейную операцию для смешивания содержимого ключевого регистра K. В частности:
- все биты в ключевом регистре являются нелинейной функцией 80-битного ключа, поставляемого пользователем к 21 раунду,
- что каждый бит в ключевом регистре после 21 раунда зависит по меньшей мере от четырех из предоставленных пользователем ключевых битов, и
- к тому времени, когда мы приходим к получению K32, шесть битов являются выражениями степени два из 80 предоставленных пользователем ключевых битов, 24 бита имеют степень три, в то время как оставшиеся биты являются функцией степени шесть или степени девять предоставленных Пользователем ключевых битов.
Мы считаем, что этих свойств достаточно, чтобы противостоять ключевым атакам на основе преобразования ключа.
6. Производительность «железа»
Мы реализовали PRESENT-80 в VHDL и адаптировали его для стандартной библиотеки ячеек Virtual Silicon (VST) на основе UMC L180 0.18 ? 1P6M Logic. Мы использовали Mentor Graphics Modelsim SE PLUS 5.8 c для моделирования и Synopsys Design Compilerversion Y-2006.06 для синтеза и моделирования мощности потребления. Были использованы типичные для литейного производства значения (1,8 Вольта для напряжения сердечника и 25°C для температуры), а для моделирования мощности применена предложенная модель проволочной нагрузки. Обратите внимание, что подобное моделирование преназначено для конструкций около 10 000 GE, поэтому результаты мощности будут пессимистичными для значительно меньших конструкций. На рисунке

показан путь данных оптимизированного по пространству PRESENT-80 без возможности дешифровки (encryption-only), который выполняет один раунд за один такт, т. е. путь данных 64-разрядной ширины. Обратите внимание, что на этапе проектирования PRESENT мы используем один и тот же S-блок 16 раз вместо того, чтобы иметь 16 различных S-блоков, и это облегчает дальнейшую сериализацию проекта, т. е. с 4-битным каналом передачи данных. Наша реализация требует 32 тактовых цикла для шифрования 64-битного открытого текста с 80-битным ключом, занимает 1570 GE и имеет в модуляции энергопотребление 5 мкВт.

Пространственные требования PRESENT
Большую часть площади занимают триггеры для хранения ключа и состояния данных, за которыми следуют S-слой и отдел XOR'ирования ключа. Битовые перестановки простой проводки увеличат площадь только тогда, когда реализация дойдет до этапа place&route. Заметим, что основной целью нашей реализации был небольшой объем аппаратного обеспечения, однако мы также синтезировали оптимизированный по мощности процесс. Для дополнительных 53 GE мы достигаем энергопотребления всего 3,3 мкВт, а нынешний-128 будет занимать оценочную площадь 1886 GE. Помимо очень малого размера PRESENT имеет довольно высокую пропускную способность, дающую хорошую энергию на бит. Сравнение с другими шифрами приведено в таблице:

7. Заключение
В этой статье мы описали новый блочный шифр PRESENT. Нашей целью был сверхлегкий шифр, который обеспечивает уровень безопасности, соизмеримый с размером 64-битного блока и 80-битным ключом. В итоге, PRESENT имеет требования к реализации, аналогичные многим компактным потоковым шифрам. Поэтому мы считаем, что он представляет как теоретический, так и практический интерес. Как и все новые предложения, мы не поощряем немедленное развертывание PRESENT, но настоятельно призываем к его анализу.
Признание
Работа, представленная в настоящем документе, была частично поддержана Европейской комиссией в рамках STREP UbiSec&Sens of the EU Framework Programme 6for Research and Development (www.ist-ubisecsens.org). Мнения и выводы, содержащиеся в настоящем документе, принадлежат авторам и не должны интерпретироваться как представляющие собой официальную политику или одобрение, выраженное или подтвержденное проектом UbiSec&Sens или Европейской комиссией.


lemproix
"состоит из 31 круга" — раунда
Качество перевода хромает
Raccooner Автор
Готов выслушать конкретные косяки и постараться их исправить
P.S. круги уже исправил.