Доброго времени суток, друзья!
Представляю Вашему вниманию перевод статьи Martin Heinz «Implementing 2D Physics in JavaScript».
Создание реалистичной анимации физических процессов может казаться сложной задачей, но это не так. Используемые для этого алгоритмы могут быть очень простыми и при этом точно воспроизводить такие физические явления, как движение, ускорение и гравитация (притяжение).
Хотите узнать, как эти алгоритмы реализуются в JS?

Примеры можно посмотреть здесь.
Исходный код находится здесь.
Начнем с движения.
Для равномерного движения мы можем использовать следующий код:
Здесь x и y — это координаты объекта, vx и vy — скорость объекта по горизонтальной и вертикальной осям, соответственно, dt (time delta — дельта времени) — время между двумя отметками таймера, что в JS равняется двум вызовам requestAnimationFrame.
Например, если мы хотим переместить объект, находящийся в точке с координатами 150, 50, на юго-запад, мы можем сделать следующее (одна отметка таймера или один шаг):
Равномерное движение — это скучно, поэтому давайте придадим нашему объекту ускорение:
Здесь ax и ay — это ускорение по осям x и y, соответственно. Мы используем ускорение для изменения скорости (vx/vy). Теперь, если мы возьмем предыдущий пример и добавим ускорение по оси x (на запад), то получим следующее:
Мы научились перемещать отдельные объекты. Как насчет того, чтобы научиться перемещать их относительно друг друга? Это называется гравитацией или притяжением. Что нам нужно сделать для этого?
Вот что мы хотим получить:

Для начала вспомним несколько уравнений из старших классов.
Сила, приложенная к телу, рассчитывается по следующей формуле:
F = m * a… сила равна массе, умноженной на ускорение
a = F / m… из этого мы можем сделать вывод, что сила действует на объект с ускорением
Если мы применим это к двум взаимодействующим объектам, то получим следующее:
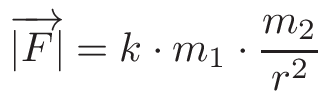
Выглядит сложно (по крайней мере, для меня), поэтому давайте разбираться. В данном уравнении |F| — это величина силы, которая одинакова для обоих объектов, но направлена в противоположные стороны. Объекты представлены массами m_1 и m_2. k — это гравитационная постоянная и r — расстояние между центрами масс объектов. Все еще непонятно? Вот иллюстрация:

Если мы хотим сделать что-то интересное, нам потребуется больше двух объектов.

На этом изображении мы видим два оранжевых объекта, притягивающих черный с силами F_1 и F_2, однако нас интересует равнодействующая сила F, которую мы можем вычислить следующим образом:
Отлично, у нас есть все необходимые расчеты. Как нам перевести это в код? Я не буду утомлять вас промежуточными этапами и сразу приведу готовый код с комментариями. Если вам понадобится больше информации, можете написать мне, я обязательно отвечу на все ваши вопросы.
Движущиеся тела иногда сталкиваются. От столкновения происходит либо выталкивание одних объектов другими, либо отскакивание одних объектов от других. Сначала поговорим о выталкивании:

Прежде всего, нам необходимо определить, что имело место столкновение:
Мы объявляем класс Collision, представляющий два столкнувшихся объекта. В функции checkCollision мы сначала вычисляем разницу между координатами x и y объектов, затем вычисляем их фактическое расстояние d. Если сумма радиусов объектов меньше, чем расстояние между ними, значит имело место столкновение этих объектов — возвращаем объект Collision.
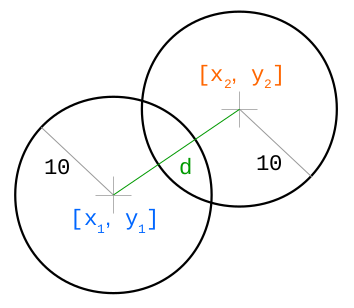
Далее нам нужно определить направление смещения и его величину (магнитуду):
n_x = d_x / d… это вектор
n_y = d_y / d
s = r_1 + r_2 — d… это «величина» столкновения (см. картинку ниже)
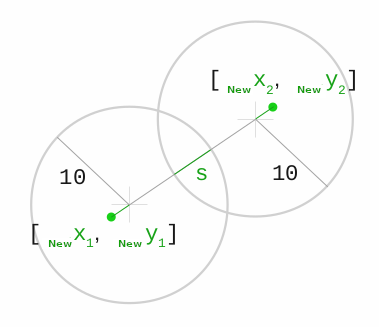
В JS это может выглядеть так:
Завершающая часть пазла — реализация отскакивания одного объекта от другого при столкновении. Я не буду приводить всех математических расчетов, поскольку это сделает статью очень длинной и скучной, ограничусь лишь тем, что упомяну о законе сохранения импульса и законе сохранения энергии, которые помогают прийти к следующей волшебной формуле:
k = -2 * ((o2.vx — o1.vx) * nx + (o2.vy — o1.vy) * ny) / (1/o1.m + 1/o2.m)… *Магия*
Как мы можем использовать волшебную k? Мы знаем, в каком направлении будут двигаться объекты, но не знаем на какое расстояние. Это и есть k. Вот как вычисляется вектор (z), показывающий, куда должны переместиться объекты:

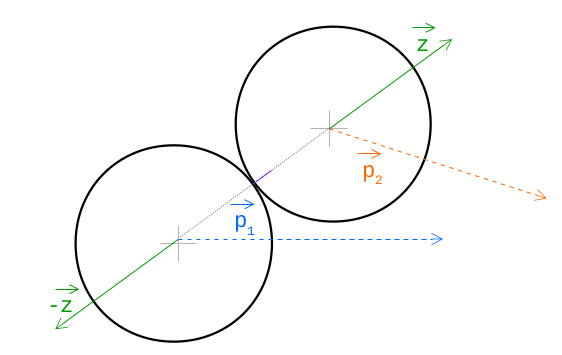
Код выглядит так:
В статье много уравнений, но большинство из них очень простые. Надеюсь, статья хоть немного помогла вам понять, как в JS реализуются физические явления и процессы.
Представляю Вашему вниманию перевод статьи Martin Heinz «Implementing 2D Physics in JavaScript».
Создание реалистичной анимации физических процессов может казаться сложной задачей, но это не так. Используемые для этого алгоритмы могут быть очень простыми и при этом точно воспроизводить такие физические явления, как движение, ускорение и гравитация (притяжение).
Хотите узнать, как эти алгоритмы реализуются в JS?

Примеры можно посмотреть здесь.
Исходный код находится здесь.
Равномерное движение и движение с ускорением
Начнем с движения.
Для равномерного движения мы можем использовать следующий код:
function move(dt) {
x += vx * dt
y += vy * dt
}
Здесь x и y — это координаты объекта, vx и vy — скорость объекта по горизонтальной и вертикальной осям, соответственно, dt (time delta — дельта времени) — время между двумя отметками таймера, что в JS равняется двум вызовам requestAnimationFrame.
Например, если мы хотим переместить объект, находящийся в точке с координатами 150, 50, на юго-запад, мы можем сделать следующее (одна отметка таймера или один шаг):
x = 150 += -1 * 0.1 - > 149.9
y = 50 += 1 * 0.1 - > 50.1
Равномерное движение — это скучно, поэтому давайте придадим нашему объекту ускорение:
function move(dt) {
vx += ax * dt
vy += ay * dt
x += vx * dt
y += vy * dt
}
Здесь ax и ay — это ускорение по осям x и y, соответственно. Мы используем ускорение для изменения скорости (vx/vy). Теперь, если мы возьмем предыдущий пример и добавим ускорение по оси x (на запад), то получим следующее:
vx = -1 += -1 * 0.1 - > -1.1 // vx += ax * dt
vy = 1 += 0 * 0.1 - > 1 // vy += ay * dt
x = 150 += -1.1 * 0.1 - > 149.89 // x += vx * dt; объект переместился дальше на -0.01
y = 50 += 1 * 0.1 - > 50.1 // y += vy * dt
Гравитация
Мы научились перемещать отдельные объекты. Как насчет того, чтобы научиться перемещать их относительно друг друга? Это называется гравитацией или притяжением. Что нам нужно сделать для этого?
Вот что мы хотим получить:

Для начала вспомним несколько уравнений из старших классов.
Сила, приложенная к телу, рассчитывается по следующей формуле:
F = m * a… сила равна массе, умноженной на ускорение
a = F / m… из этого мы можем сделать вывод, что сила действует на объект с ускорением
Если мы применим это к двум взаимодействующим объектам, то получим следующее:
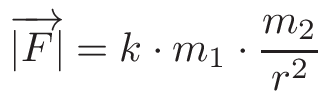
Выглядит сложно (по крайней мере, для меня), поэтому давайте разбираться. В данном уравнении |F| — это величина силы, которая одинакова для обоих объектов, но направлена в противоположные стороны. Объекты представлены массами m_1 и m_2. k — это гравитационная постоянная и r — расстояние между центрами масс объектов. Все еще непонятно? Вот иллюстрация:

Если мы хотим сделать что-то интересное, нам потребуется больше двух объектов.

На этом изображении мы видим два оранжевых объекта, притягивающих черный с силами F_1 и F_2, однако нас интересует равнодействующая сила F, которую мы можем вычислить следующим образом:
- сначала мы рассчитываем силы F_1 и F_2, используя предыдущую формулу:

- затем переводим все в векторы:
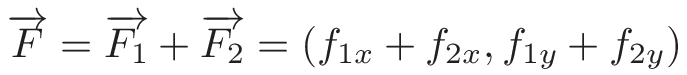
Отлично, у нас есть все необходимые расчеты. Как нам перевести это в код? Я не буду утомлять вас промежуточными этапами и сразу приведу готовый код с комментариями. Если вам понадобится больше информации, можете написать мне, я обязательно отвечу на все ваши вопросы.
function moveWithGravity(dt, o) { // o - массива объектов, с которыми мы работаем
for (let o1 of o) { // нулевой счетчик (сумматор) сил каждого объекта
o1.fx = 0
o1.fy = 0
}
for (let [i, o1] of o.entries()) { // для каждой пары объектов
for (let [j, o2] of o.entries()) {
if (i < j) { // чтобы не делать одного и того же для той же пары дважды
let dx = o2.x - o1.x // вычисляем расстояние между центрами объектов
let dy = o2.y - o1.y
let r = Math.sqrt(Math.pow(dx, 2) + Math.pow(dy, 2))
if (r < 1) { // чтобы избежать деления на 0
r = 1
}
// вычисляем равнодействующую для этой пары; k = 1000
let f = (1000 * o1.m * o2.m) / Math.pow(r, 2)
let fx = f * dx / r
let fy = f * dy / r
o1.fx += fx // сила первого объекта
o1.fy += fy
o2.fx -= fx // сила второго объекта в противоположной направлении
o2.fy -= fy
}
}
}
for (let o1 of o) { // для каждого объекта обновляем...
let ax = o1.fx / o1.m // ускорение
let ay = o1.fy / o1.m
o1.vx += ax * dt // скорость
o1.vy += ay * dt
o1.x += o1.vx * dt // позицию
o1.y += o1.vy * dt
}
}
Столкновение
Движущиеся тела иногда сталкиваются. От столкновения происходит либо выталкивание одних объектов другими, либо отскакивание одних объектов от других. Сначала поговорим о выталкивании:

Прежде всего, нам необходимо определить, что имело место столкновение:
class Collision {
constructor(o1, o2, dx, dy, d) {
this.o1 = o1
this.o2 = o2
this.dx = dx
this.dy = dy
this.d = d
}
}
function checkCollision(o1, o2) {
let dx = o2.x - o1.x
let dy = o2.y - o1.y
let d = Math.sqrt(Math.pow(dx, 2) + Math.pow(dy, 2))
if(d < o1.r + o2.r){
return {
collisionInfo: new Collision(o1, o2, dx, dy, d),
collided: true
}
}
return {
collisionInfo: null,
collided: false
}
}
Мы объявляем класс Collision, представляющий два столкнувшихся объекта. В функции checkCollision мы сначала вычисляем разницу между координатами x и y объектов, затем вычисляем их фактическое расстояние d. Если сумма радиусов объектов меньше, чем расстояние между ними, значит имело место столкновение этих объектов — возвращаем объект Collision.

Далее нам нужно определить направление смещения и его величину (магнитуду):
n_x = d_x / d… это вектор
n_y = d_y / d
s = r_1 + r_2 — d… это «величина» столкновения (см. картинку ниже)

В JS это может выглядеть так:
function resolveCollision(info){ // "info" - это объект Collision из предыдущего примера
let nx = info.dx / info.d // вычисляем векторы
let ny = info.dy / info.d
let s = info.o1.r + info.o2.r - info.d // вычисляем глубину проникновения
info.o1.x -= nx * s/2 // сдвигаем первый объект на половину величины столкновения
info.o1.y -= ny * s/2
info.o2.x += nx * s/2 // сдвигаем второй объект в противоположную сторону
info.o2.y += ny * s/2
}
Отскакивание
Завершающая часть пазла — реализация отскакивания одного объекта от другого при столкновении. Я не буду приводить всех математических расчетов, поскольку это сделает статью очень длинной и скучной, ограничусь лишь тем, что упомяну о законе сохранения импульса и законе сохранения энергии, которые помогают прийти к следующей волшебной формуле:
k = -2 * ((o2.vx — o1.vx) * nx + (o2.vy — o1.vy) * ny) / (1/o1.m + 1/o2.m)… *Магия*
Как мы можем использовать волшебную k? Мы знаем, в каком направлении будут двигаться объекты, но не знаем на какое расстояние. Это и есть k. Вот как вычисляется вектор (z), показывающий, куда должны переместиться объекты:


Код выглядит так:
function resolveCollisionWithBounce(info){
let nx = info.dx / info.dy
let ny = info.dy / info.d
let s = info.o1.r + info.o2.r - info.d
info.o1.x -= nx * s/2
info.o1.y -= ny * s/2
info.o2.x += nx * s/2
info.o2.y += ny * s/2
// магия...
let k = -2 ((info.o2.vx - info.o1.vx) * nx + (info.o2.vy - info.o1.vy) * ny) / (1/info.o1.m + 1/info.o2.m)
info.o1.vx -= k * nx / info.o1.m // то же самое, только добавили "k" и поменяли "s/2" на "m"
info.o1.vy -= k * ny / info.o1.m
info.o2.vx += k * nx / info.o2.m
info.o2.vy += k * ny / info.o2.m
}
Заключение
В статье много уравнений, но большинство из них очень простые. Надеюсь, статья хоть немного помогла вам понять, как в JS реализуются физические явления и процессы.


sshikov
Сила равна массе, умноженной на скорость…
Мда. А старина Ньютон и не знает
sshikov
О, оперативно…
Кстати, то что вы делаете — это фактически интегрирование уравнений движения. И его было бы намного лучше делать явно — т.е. путем явной записи уравнений как функций JS, и отдельной записи алгоритма численного интегрирования. А иначе любое изменение приводит к переписыванию всего и вся.
akryukov
Это перевод, вряд ли автор будет значительно переписывать код в рамках этой статьи
sshikov
Ну, автор может и не будет — но возможно кто-то прочитает.