Представьте, что вы хотите научиться живописи, а вам объясняют, как красиво и хорошо покрасить забор, вместо того чтобы показать картины Ван Гога, Пикассо или других великих художников, и даже не говорят вам о том, что они существуют. К сожалению, изучение математики в школах порой напоминает процесс наблюдения за тем, как сохнет и трескается краска на деревянной доске. В этой книге известный математик Эдуард Френкель открывает доселе скрытые стороны математики, позволяя нам увидеть в ней красоту и элегантность, свойственные только величайшим шедеврам. «Математика, — говорит он, — это портал в неизведанный мир, ключ к пониманию глубинных тайн Вселенной и нас самих». Великий математик приглашает всех нас в этот таинственный мир.

Глава 2. Суть симметрии

В умах большинства людей математика неразрывно связана с числами. Математики для них — это люди, которые целыми днями просиживают над расчетами и оперируют числами: большими числами, огромными числами, числами с необычными, экстравагантными названиями. Я тоже так думал — по крайней мере, до тех пор, пока Евгений Евгеньевич не познакомил меня с концепциями и идеями современной математики. Одна из них оказалась ключом к обнаружению кварков. Это была концепция симметрии.Что такое симметрия? На интуитивном уровне мы все это прекрасно знаем. Мы с первого взгляда распознаем симметрию в окружающих нас предметах, не требуя дополнительных пояснений. Если попросить человека привести пример симметричного объекта, то он вспомнит бабочку, снежинку или укажет на симметричность человеческого тела.

Однако на вопрос, что же он в действительности подразумевает, когда говорит, что предмет симметричен, большинство вразумительно ответить не может. Вот как объяснил мне это Евгений Евгеньевич.

— Взглянем на эти два стола — круглый и квадратный, — он указал на столы в своем кабинете.

— Какой из них более симметричный?

— Круглый, конечно. Разве это не очевидно?

— Но почему? Быть математиком означает не принимать ничего «очевидного» как должное, а пытаться обосновать каждое утверждение. Ты удивишься, но очень часто самый очевидный ответ оказывается неверным.

Заметив мое замешательство, Евгений Евгеньевич сжалился:

— Какое свойство круглого стола делает его более симметричным?

Я немного подумал, и меня озарило:

— Наверное, симметрия объекта заключается в том, что он сохраняет свою форму и позицию, даже если мы каким-то образом меняем его.

Евгений Евгеньевич кивнул.

— Так и есть. Давай рассмотрим возможные преобразования двух столов, при которых их формы и позиции будут сохраняться, — сказал он. — В случае круглого стола…

Я не дал ему закончить:

— Подойдет любое вращение вокруг центра. Мы получим тот же самый стол в той же самой позиции. Но если применить произвольное вращение к квадратному столу, то в большинстве случаев результат будет отличаться от исходной конфигурации. Сохранит форму и позицию стола только вращение на угол 90 градусов и кратные ему углы.

— Точно! Если ты на секунду выйдешь из моего кабинета, и я поверну круглый стол на любой угол, то по возвращении ты не заметишь разницы. Однако если я проделаю то же самое с квадратным столом, то отличие будет очевидно — если только я не поверну его на 90, 180 или 270 градусов.

Он продолжил:

— Такие преобразования называются симметриями. Теперь ты видишь, что у квадратного стола только четыре симметрии. У круглого стола их намного больше — в действительности бесконечно много. Именно поэтому мы говорим, что круглый стол более симметричный.

Это расставляло все по своим местам.

— Все это довольно очевидно, — продолжал Евгений Евгеньевич. — Не нужно быть математиком, чтобы заметить эти свойства.Настоящий же математик задаст такой вопрос: каковы все возможные симметрии конкретного объекта? Взглянем на квадратный стол. Его симметрии — это четыре вращения вокруг центра: на 90, 180, 270 и 360 градусов против часовой стрелки. Математик скажет, что множество симметрий квадратного стола включает четыре элемента, соответствующих углам в 90, 180, 270 и 360 градусов. Мы сопоставим их четырем вершинам стола — каждое вращение переводит выбранную вершину (отмеченную кружком на рис. 2.3) в одно из угловых положений.

Одно из этих положений особенное, не похожее на другие, — это вращение на 360 градусов. По сути, это то же самое, что вращение на 0 градусов, то есть полный оборот соответствует полному отсутствию вращения. И действительно, после такого вращения каждая точка стола оказывается в точности в том же положении, где она была до этого. Это особая симметрия, никак не влияющая на позицию объекта. Ее называют тождественной симметрией или просто тождеством.

Обратите внимание, что вращение на любой угол свыше 360 градусов эквивалентно вращению на угол между 0 и 360 градусами. Например, вращение на 450 градусов эквивалентно вращению на 90 градусов, так как 450 = 360 + 90. Вот почему мы рассматриваем только вращение на углы от 0 до 360 градусов.

Это позволяет нам сделать важнейшее наблюдение: если последовательно применить к столу два вращения из списка {90°, 180°, 270°, 360°}, то результат будет абсолютно таким же, как если бы мы применили другое вращение из того же самого списка. Другими словами, симметрии можно компоновать! Это также очевидно: любые две симметрии сохраняют позицию стола, следовательно, их композиция также сохранит ее. Таким образом, композиция симметрий также является симметрией. Например, если мы повернем стол на 90 градусов, а затем еще на 180 градусов, то в сумме получим вращение на 270 градусов. Давай посмотрим, что происходит со столом при применении этих симметрий. Когда мы поворачиваем его против часовой стрелки на 90 градусов, правая вершина стола (отмеченная кружком на рис. 2.3) перемещается в верхний угол картинки. Затем мы применяем вращение на 180 градусов, и верхняя вершина стола переходит в нижний угол. Окончательный результат таков, что правая вершина стола перемещается в нижний угол рисунка. Это результат был бы достигнут и при единичном вращении против часовой стрелки на 270 градусов.

Вот еще один пример:

Выполнив вращение на 90 градусов, а затем еще на 270 градусов, мы получаем суммарное вращение на 360 градусов. Однако результат вращения на 360 градусов абсолютно идентичен вращению на 0 градусов. Как мы уже говорили выше, это тождественная симметрия. Другими словами, второе вращение (на 270 градусов) отменяет результат первого вращения (на 90 градусов). Это действительно чрезвычайно важное свойство: любую симметрию можно обратить. Это означает, что для любой симметрии S существует другая симметрия S', такая, что их композиция образует тождественную симметрию. S' называют обратной симметрией для S, или инверсией. Итак, мы увидели, что вращение на 270 градусов является инверсией вращения на 90 градусов.4 Мы убедились, что простой набор симметрий квадратного стола — четыре вращения {90°, 180°, 270°, 360°} — на самом деле совсем не так прост. Он обладает сложной внутренней структурой: существуют определенные правила, которым подчиняются взаимодействия членов этого множества. Во-первых, мы можем скомпоновать или суммировать любые две симметрии. Во-вторых, существует особая симметрия — тождественная. В нашем примере это вращение на 0 градусов. Если мы суммируем ее с любой другой симметрией, то в результате получим ту же самую симметрию в неизменном виде. Например,

$\$\$display\$\$90°\; +\; 0°\; =\; 90°,\; 180°\; +\; 0°\; =\; 180°\; и\; т.\; д.\$\$display\$\$$

И, в-третьих, для любой симметрии S существует обратная (инверсная) симметрия S', такая, что в сумме симметрии S и S' дают нам тождество. А теперь — барабанная дробь! Множество вращений вместе с этими тремя правилами образуют пример того, что в математике называется группой.

Симметрии любого другого объекта также образуют группу. В общем случае группа включает намного больше элементов, чем рассматриваемые здесь четыре вращения, — их даже может быть бесконечно много.5 Давайте посмотрим теперь, как все это работает в случае круглого стола. Мы уже поднабрались опыта и поэтому понимаем, что множество симметрий круглого стола представляет собой набор абсолютно всех возможных вращений (причем не только на углы, кратные 90 градусам!), а визуализировать его мы можем как набор из всех точек окружности. Каждая точка на этой окружности соответствует углу ? в диапазоне от 0 до 360 градусов и представляет вращение круглого стола на данный угол в направлении против часовой стрелки. В частности, есть особая точка, соответствующая вращению на 0 градусов. Она обозначена черным кружком на рис. 2.4, как и другая точка, соответствующая вращению на 30 градусов.

Теперь посмотрим, применимы ли перечисленные выше три правила к множеству точек на окружности. Во-первых, композиция двух вращений — на ?1 и ?2 градусов — представляет собой вращение на ?1 + ?2 градусов. Если сумма ?1 + ?2 больше 360 градусов, то мы всего лишь вычитаем из нее «лишние» 360 градусов. В математике это называется сложением по модулю 360. Например, если ?1 = 195°, а ?2 = 250°, то сумма двух углов составляет 445 градусов. Вращение на 445 градусов эквивалентно вращению на 85 градусов. Таким образом, в группе вращений круглого стола верно следующее:

Во-вторых, на окружности есть особая точка, соответствующая вращению на 0 градусов. Это элемент тождественности данной группы. И наконец, инверсия вращения на ? градусов против часовой стрелки — это вращение против часовой стрелки на (360 – ?) градусов или, что то же самое, вращение на ? градусов по часовой стрелке (рис. 2.5).

Итак, мы описали группу вращений круглого стола. Мы будем называть ее группой окружности. В отличие от группы симметрий квадратного стола, в которую входит четыре элемента, в этой группе бесконечно много элементов, так как между отметками 0 и 360 градусов помещается бесконечное число углов.

Теперь под наше интуитивное понимание симметрии мы подвели твердое теоретическое основание — по сути, мы превратили симметрию в математическую концепцию.

Прежде всего, мы объявили, что симметрия объекта — это преобразование, сохраняющее сам объект и его свойства. Затем мы сделали решающий шаг: перенесли внимание с объекта как такового на множество всех его симметрий. В случае квадратного стола это множество из четырех элементов (вращения на углы, кратные 90 градусам), а множество симметрий круглого стола бесконечно велико (все точки окружности). Наконец, мы описали точные правила, которые всегда выполняются в этих наборах симметрий: две симметрии можно сложить и получить в результате третью симметрию; обязательно должен существовать тождественный элемент; для каждой симметрии существует обратная. (Композиция симметрий также удовлетворяет свойству ассоциативности, описанному в примечании 4.) Таким образом, мы пришли к математической концепции группы.

Группа симметрий — это абстрактный объект, совершенно не похожий на те реальные объекты, о которых шла речь в начале нашего разговора. В отличие от самого стола, невозможно потрогать или подержать в руках множество его симметрий. Однако мы можем вообразить его, нарисовать его элементы, изучить и обсудить это множество. Кроме того, у каждого элемента такого абстрактного множества есть точное и конкретное значение: он представляет одно из возможных преобразований реального объекта — его симметрию.

Математика — это наука, изучающая подобные абстрактные объекты и концепции.

Опыт показывает, что симметрия — это основополагающий, руководящий принцип законов природы. Например, снежинка принимает форму идеального шестиугольника, потому что, как выясняется, это состояние с минимальной энергией, в котором способны кристаллизоваться молекулы воды.

Набор симметрий снежинки составляют вращения на углы, кратные 60 градусам, то есть на 60, 120, 180, 240, 300 и 360 градусов (последнее эквивалентно повороту на 0 градусов). Помимо этого, мы можем «перевернуть» снежинку относительно каждой из шести осей, соответствующих этим углам. Все эти вращения и перевороты сохраняют форму и позицию снежники; следовательно, они являются ее симметриями.*

Если перевернуть бабочку, то она будет лежать перед нами кверху лапками. Поскольку с одной стороны у нее растут лапки, а с другой их нет, то переворот, строго говоря, не является симметрией бабочки. Когда мы говорим, что бабочка симметрична, мы имеем в виду ее идеализированную версию, у которой передняя и задняя стороны абсолютно идентичны (в отличие от брюшка и спинки настоящей бабочки). В таком идеализированном представлении переворот бабочки попросту меняет местами левое и правое крылышки и, следовательно, становится симметрией. (Также можно представить замену правого крылышка на левое и наоборот без переворота бабочки кверху лапками.)

Это вынуждает нас поднять важный вопрос: в природе существует множество объектов, обладающих приблизительной симметрией. Настоящий стол не идеально круглый или квадратный, живая бабочка выглядит по-разному при взгляде на нее сверху и снизу, левая и правая стороны человеческого тела также различаются. Однако даже в подобных ситуациях бывает полезно абстрагироваться от несовершенства реального мира и рассматривать идеализированные версии или модели объектов: идеально круглый стол или изображение бабочки, на котором спинка ничем не отличается от брюшка. Это дает нам возможность исследовать симметрии идеализированных объектов, а полученные на основе такого анализа результаты мы затем можем скорректировать с учетом отличий реальных объектов от их моделей.

Не следует думать, что мы не ценим асимметрию, — конечно же, ценим и часто находим в ней красоту. Однако суть математической теории симметрии лежит не в эстетической плоскости. Она заключается в том, чтобы сформулировать концепцию симметрии в самых общих и — неизбежно — самых абстрактных терминах, для того чтобы сделать ее одинаково применимой к объектам из самых разных областей знания, будь то геометрия, теория чисел, топология, физика, химия, биология и т. п. После того как такая теория разработана, мы можем начинать говорить о механизмах нарушения симметрии — рассматривать возникновение асимметрии. Например, элементарные частицы набирают массу вследствие нарушения так называемой калибровочной симметрии. Этому способствует бозон Хиггса — трудноуловимая частица, которую ученые недавно открыли в ходе экспериментов на большом адронном коллайдере под Женевой.6 Изучение подобных механизмов нарушения симметрии позволяет нам получать бесценную информацию о поведении фундаментальных строительных кирпичиков природы.

Обратите внимание на то, что переворот стола не относится к числу симметрий: стол при этом оказывается столешницей вниз, а ножками кверху — давайте не забывать, что у этого предмета мебели есть ножки. Если бы мы рассматривали просто квадрат или круг (без ножек), то перевороты были бы самыми настоящими симметриями, и мы могли бы включить их в соответствующие группы симметрий.

Мне хотелось бы отдельно подчеркнуть некоторые базовые качества абстрактной теории симметрии, так как они великолепно иллюстрируют значимость математики.

Первое качество — это универсальность. Группа окружности служит группой симметрий не только круглого стола, но и других круглых объектов, таких как стакан, бутылка, колонна и т. п. На самом деле, назвать объект круглым и сказать, что группа его симметрий представляет собой группу окружности, — одно и то же. Это чрезвычайно сильное заявление: мы понимаем, что способны описать важный атрибут объекта («круглый»), всего лишь указав на его группу симметрий («окружность»). Точно так же заявление о «квадратном» объекте означает, что группа симметрий данного объекта представляет собой описанную выше группу из четырех элементов. Другими словами, один и тот же математический объект (например, группа окружности) описывает множество разнообразных конкретных предметов, указывая на общие для всех них универсальные свойства (такие, как «округлость»).

Второе качество — объективность. Концепция группы нисколько не зависит от нашей ее интерпретации. Кто бы ни решился исследовать ее, для всех она будет означать одно и то же. Разумеется, чтобы понять эту концепцию, необходимо знать язык, используемый для ее описания, — язык математики. Но его может выучить каждый. Человеку, желающему усвоить смысл знаменитого утверждения Рене Декарта: «Je pense, doncje suis», необходимо знать французский язык (по крайней мере, понимать слова, из которых состоит фраза) — и это тоже доступно каждому. Однако в случае философского утверждения, даже если относительно его буквального перевода разногласий не возникнет, интерпретации могут быть самыми разными. Более того, одну и ту же интерпретацию кто-то будет считать истинной, а кто-то ложной. В противоположность этому смысл логически непротиворечивого математического утверждения не допускает двояких интерпретаций; точно так же его истинность всегда объективна. (В целом, истинность конкретного утверждения может зависеть от системы аксиом, в рамках которой оно рассматривается. Тем не менее даже в этом случае зависимость от аксиом также объективна.) Например, утверждение «группа симметрий круглого стола является окружностью» истинно для всех, всегда и везде. Другими словами, математические истины — необходимые истины. Мы подробнее поговорим об этом в главе 18.

Третье качество, тесно связанное с первыми двумя, — это долговечность. Теорема Пифагора, без сомнения, означала для древних греков то же самое, что и для нас сегодня, и нет никаких оснований опасаться, что ее смысл может измениться в будущем. Точно так же все истинные математические утверждения, о которых мы говорим в этой книге, останутся в силе навечно.

Факт наличия такого объективного и долговечного знания (к тому же принадлежащего в равной степени всем нам) — вовсе не чудо, как многие могут полагать. Считается, что математические концепции существуют в так называемом Платоническом мире — собственном пространстве, отдельном от физического и интеллектуального миров (мы подробнее поговорим об этом в последней главе книги). До сих пор так до конца и не понятно, что это в действительности такое и какие факторы подталкивают людей к тому, чтобы делать все новые и новые математические открытия. Очевидно лишь, что роль скрытой реальности в нашей жизни будет в дальнейшем лишь возрастать, особенно с учетом распространения новых компьютерных технологий и технологий трехмерной печати.

Четвертое качество — это применимость математических идей к реальному миру. Например, благодаря тому, что ученые взглянули на элементарные частицы и взаимодействия между ними с точки зрения концепции симметрии, в квантовой физике за последние пятьдесят лет произошел огромный скачок вперед. Частицы, такие как электроны или кварки, ничем, по сути, не отличаются от круглых столов или снежинок, чье поведение в огромной степени определяется их симметриями (какие-то симметрии точные, а какие-то приблизительные).

Превосходной иллюстрацией служит история с открытием кварков. Из книг, которыми поделился со мной Евгений Евгеньевич, я узнал, что в основе классификации адронов Гелл-Мана и Неэмана, о которой я упоминал в предыдущей главе, лежит группа симметрий. Хотя математики уже исследовали эту группу раньше, они даже не догадывались о существовании какой-либо связи между ней и субатомными частицами или чем-то подобным. Математическое название группы — SU(3). За буквами S и U скрывается выражение special unitary — «специальная унитарная». По своим свойствам эта группа напоминает группу симметрий сферы, которую мы в деталях обсудим в главе 10.

Слово «представление» имеет в математике особый смысл, отличный от того, к которому мы привыкли в повседневной жизни. Позвольте мне отвлечься на минутку и пояснить, что этот термин означает в текущем контексте. Наверное, проще всего это сделать на примере. Вспомните группу вращений круглого стола, которую мы обсуждали чуть выше, — группу окружности. Теперь представьте, что наш стол начал расти вширь и теперь простирается бесконечно во все стороны. Растянув его таким способом, мы получили абстрактный математический объект —плоскость. Каждое вращение стола вокруг центра порождает поворот этой плоскости вокруг той же самой точки. Таким образом, мы сформировали правило, связывающее одну из симметрий(вращений) плоскости с каждым элементом группы окружности. Другими словами, каждый элемент группы окружности может быть представлен той или иной симметрией плоскости. Вот почему математики называют этот процесс представлением группы окружности.

Мы знаем, что плоскость двумерная, ведь у нее две оси координат, а значит, каждая точка также обозначается двумя координатами.

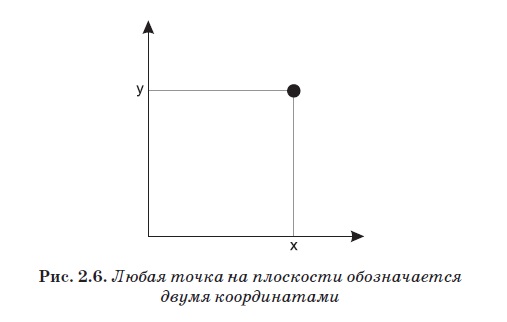
Следовательно, можно утверждать, что мы создали «двумерное представление» группы вращений. Это всего лишь означает, что каждый элемент группы вращений теперь воплощен в виде симметрии плоскости.

Существуют не только двумерные пространства — плоскости, но и пространства с большим числом измерений. Например, мыс вами живем в трехмерном пространстве. Это означает, что у него три оси координат, и для того чтобы указать позицию любой точки, нам нужно сообщить три ее координаты (x, y, z), как показано на рис. 2.7.

Невозможно вообразить четырехмерное пространство, но математика предоставляет нам универсальный язык, позволяющий рассуждать о пространствах любой размерности. На этом языке мы описываем точки четырехмерного пространства с помощью четверок чисел
(x, y, z, t) — аналогично точкам трехмерного пространства, которые представляются тройками (x, y, z). Точно также можно описать точку любого n-мерного пространства (где n — натуральное число), используя набор из n чисел. Если вы когда-либо пользовались программами для работы с электронными таблицами, то вам знакомы такие наборы: один набор — это одна строка таблицы, а каждое из n чисел в строке соответствует одному конкретному атрибуту данных. Таким образом, каждая строка таблицы описывает одну точку в n-мерном пространстве. (В главе 10 мы подробнее поговорим о пространствах различной размерности.)

Если каждому элементу группы можно согласованным образом сопоставить одну из симметрий n-мерного пространства, то можно сказать, что данная группа обладает «n-мерным представлением».

Оказывается, группа может обладать представлениями разной размерности. Вот почему элементарные частицы можно сгруппировать в семейства из восьми или десяти частиц: у группы SU(3) есть как 8-мерные, так и 10-мерные представления. Во-семь частиц в каждом октете из определенных Гелл-Маном и Неэманом (как тот, что изображен на рис. 1.4) взаимно однозначно соответствуют восьми осям координат 8-мерного пространства, являющегося представлением группы SU(3). Аналогично и с декуплетами частиц. (В то же время частицы невозможно объединить в семейства из, скажем, семи или одиннадцати штук —математики доказали, что у группы SU(3) нет 7- и 11-мерныхпредставлений.)

Поначалу это считалось всего лишь удобным способом группировки частиц, обладающих схожими свойствами. Однако Гелл-Ман пошел дальше: он объявил о существовании веских причин, обосновывающих такую схему классификации. В сущности, он объяснил, что данная схема потому так хорошо и работает, что адроны состоят из еще более мелких частиц — кварков. Одни типы адронов состоят из двух кварков, другие — из трех. Независимо от Гелл-Мана схожее предположение выдвинул физик Джордж Цвейг (предложивший для этих мелких частиц другое название — «тузы»).

Это было ошеломляющее заявление. Оно не только шло вразрез с бытовавшим в то время убеждением, будто протоны, нейтроны и другие адроны неделимы; подразумевалось также, что новые частицы должны обладать электрическими зарядами, по величине равными доле заряда электрона. Это предсказание взбудоражило все научное общество, ведь никому еще не удавалось обнаружить ничего подобного. Тем не менее существование кварков совсем скоро было подтверждено экспериментально, и в точном соответствии с прогнозами они действительно обладали дробными зарядами!

Что же натолкнуло Гелл-Мана и Цвейга на мысль о существовании кварков? Это была математическая теория представлений группы SU(3), и в частности тот факт, что у группы SU(3) есть два разных трехмерных представления (на самом деле, как раз поэтому в названии группы и присутствует цифра 3).

Гелл-Мани Цвейг предположили, что эти два представления должны описывать два семейства фундаментальных частиц: из трех кварков и трех антикварков. Кроме того, как оказалось, 8- и 10-мерные представления группы SU(3) также легко конструируются на основе трехмерных. И это дает нам точную «схему сборки» адронов из кварков — прямо как в конструкторе «Лего». Гелл-Ман назвал три этих кварка «верхним», «нижним» и «странным». Протон состоит из двух верхних кварков и одного нижнего, а нейтрон — из двух нижних кварков и одного верхнего (см. рис. 1.2 и 1.3). Обе эти частицы принадлежат октету, показанному на рис. 1.4. Другие частицы в данном октете включают в себя и странный кварк. Существуют также октеты частиц, каждая из которых представляет собой ту или иную композицию из одного кварка и одного антикварка.

Открытие кварков — превосходный пример того, о чем мы уже говорили во введении: математика действительно играет первостепенную роль в истории научных открытий. Существование этих частиц было предсказано не на основе эмпирических данных — ученые отталкивались исключительно от математических моделей симметрий. Это было чисто теоретическое предположение, сделанное в рамках сложной математической теории представлений группы SU(3). Для того чтобы овладеть этой теорией, физикам потребовались годы (и, к слову, многие поначалу противились ее внедрению), однако сегодня развитие физики элементарных частиц без нее попросту немыслимо. Теория представлений не только предоставила удобный способ классификации адронов, но также привела к открытию кварков — событию, навеки изменившему наше представление о физической реальности.

Только представьте себе: казалось бы, доступная лишь немногим математическая теория позволила нам добраться до самой сути того, как и из чего построен наш мир. Невозможно не
поддаваться очарованию волшебной гармонии этих крохотных фрагментов материи, не восхищаться умением математиков выявлять глубинные процессы, заставляющие крутиться шестеренки Вселенной!

Рассказывают, будто жена Альберта Эйнштейна, услышав, что для определения формы пространства — времени необходимо прибегнуть к помощи телескопа из обсерватории Маунт-Вилсон, обронила: «Надо же, а мой муж делает то же самое на обороте старого конверта». Физикам, конечно, необходимо изощренное дорогое оборудование, например большой адронный коллайдер в Женеве. Тем более поразителен тот факт, что ученые, такие как Эйнштейн и Гелл-Ман, вскрывали глубочайшие секреты окружающего мира с помощью того, что, на первый взгляд, кажется исключительно теоретическим и совершенно абстрактным математическим знанием.

Не важно, кто мы такие и во что верим, — все мы являемся хранителями этого знания. Оно объединяет нас и открывает новые, доселе неизведанные стороны нашей любви к Вселенной.

» Более подробно с книгой можно ознакомиться на сайте издательства
» Оглавление
» Отрывок

Для Хаброжителей скидка 25% по купону — Френкель

По факту оплаты бумажной версии книги на e-mail высылается электронная книга.