По состоянию на 9 марта 2020 мы имеем резкое снижение рынков США начиная с исторического максимума в 20-числах февраля 2020, которое на данный момент составило около -16%. Новости пестрят заголовками про надвигающуюся рецессию из-за коронавируса, Россия вышла из сделки Опек+, что ударило по ценам на нефть (-20% за день) и завтра, (10 марта 2020) ожидается снижение рынка ММВБ также на 20%, судя по котировкам наших акций на западных рынках.


Ждет ли нас глобальная рецессия? В этой статье мы попробуем разобраться как можно заранее увидеть сигналы начала рецессии средствами Python.

Для ответа на поставленный вопрос мы попробуем использовать доходности облигаций, акций и технический анализ. Мы будем использовать исторические данные с финансового рынка США, как первого по объему фондового рынка в мире. По сути, если в США начнется рецессия, она начнется во всем мире (как это произошло в 2008 году). Также, для нас удобно то, что для рынка США есть данные за десятилетия, что позволит провести анализ на значительном историческом промежутке.

Исторические данные мы будем брать из Yahoo Finance с помощью библиотеки yfinance , с сайта фед. резерва США с помощью библиотеки fredapi и с сайта Quandl с различной финансовой информацией через pandas_datareader. Обращаю внимание, что для Fed и Quandl нужно зарегистрироваться для получения ключа API (это бесплатно).

Все финансовые кризисы в США мы будем отмечать серыми областями непосредственно на графиках.


Получаем исторические данные по S&P500 с Yahoo, спреды доходностей облигаций с FRED и индекс накопленной доходности по облигациям с FRED:

GSPC_h = yfinance.download("^GSPC", start="1962-01-01", end="2020-03-09") #SNP500
T10YFF = fred.get_series('T10YFF', observation_start='1962-01-01', observation_end='2020-03-09') #10YB-FFR
T10Y2Y = fred.get_series('T10Y2Y', observation_start='1976-06-01', observation_end='2020-03-09') #10YB-2YB
# ICE BofA US Corp 10-15yr Total Return Index Value
BAMLCC7A01015YTRIV = fred.get_series('BAMLCC7A01015YTRIV', observation_start='1962-01-01', observation_end='2020-03-09')

Премия за риск

Премия за риск является показателем, отражающим дополнительную доходность, которую получит инвестор, приняв на себя повышенный риск.

Так работают финансовые рынки — чем выше доходность вложения, тем выше риск.

Для того, чтобы рассчитать премию за риск нужно вычесть из ожидаемой доходности рискового актива, безрисковую ставку доходности.

Для рынка США, безрисковой ставкой доходности является ставка фед.резерва США (аналог ключевой ставки у нас) — FED.

Премия за риск для акций и облигаций считается по разному.
Для облигаций: доходность облигации (Yield) минус FED.
Для акций: показатель Прибыль/Цена (E/P) минус FED,
где прибыль — это прибыль компании за год, цена — цена акции на момент расчета показателя.

Для расчета доходности акции мы берем не выплаченные дивиденды в качестве доходности, а прибыль, полученную компанией, потому что дивиденды это лишь часть полученной прибыли, которую компания выплачивает акционерам. Становясь владельцем компании через покупку ее акций, фактически, конечным доходом для нас будет именно прибыль, которая будет распределена среди акционеров в полном объеме в момент ликвидации компании.

Получаем E/P для S&P500 (SP500_EARNINGS_YIELD_MONTH), безрисковую ставку (FED Funds Rate) и доходность корпоративных облигаций широкого рынка (Baa Bonds Yield):

# E/P
symbol = 'MULTPL/SP500_EARNINGS_YIELD_MONTH'
SP500_EARNINGS_YIELD_MONTH = web.DataReader(symbol, 'quandl', '1962-01-01', '2020-03-09')
# FED Funds Rate
FEDFUNDS = fred.get_series('FEDFUNDS', observation_start='1962-01-01', observation_end='2020-03-09')
# Baa Bonds Yield
BAA = fred.get_series('BAA', observation_start='1962-01-01', observation_end='2020-03-09')

Посчитаем премию за риск как доходность минус безрисковая ставка:

# премия за риск для акций
risk_premium = pd.concat([SP500_EARNINGS_YIELD_MONTH, FEDFUNDS],axis=1).fillna(method='bfill')
risk_premium['premium'] = risk_premium['Value'] - risk_premium[0]

# пермия за риск для облигаций
risk_premium_b = pd.concat([BAA, FEDFUNDS],axis=1).fillna(method='bfill')
risk_premium_b.columns = ['BAA', 'FEDFUNDS']
risk_premium_b['premium_b'] = risk_premium_b['BAA'] - risk_premium_b['FEDFUNDS']

Посмотрим что получилось для акций и облигаций в отдельности

Для акций:




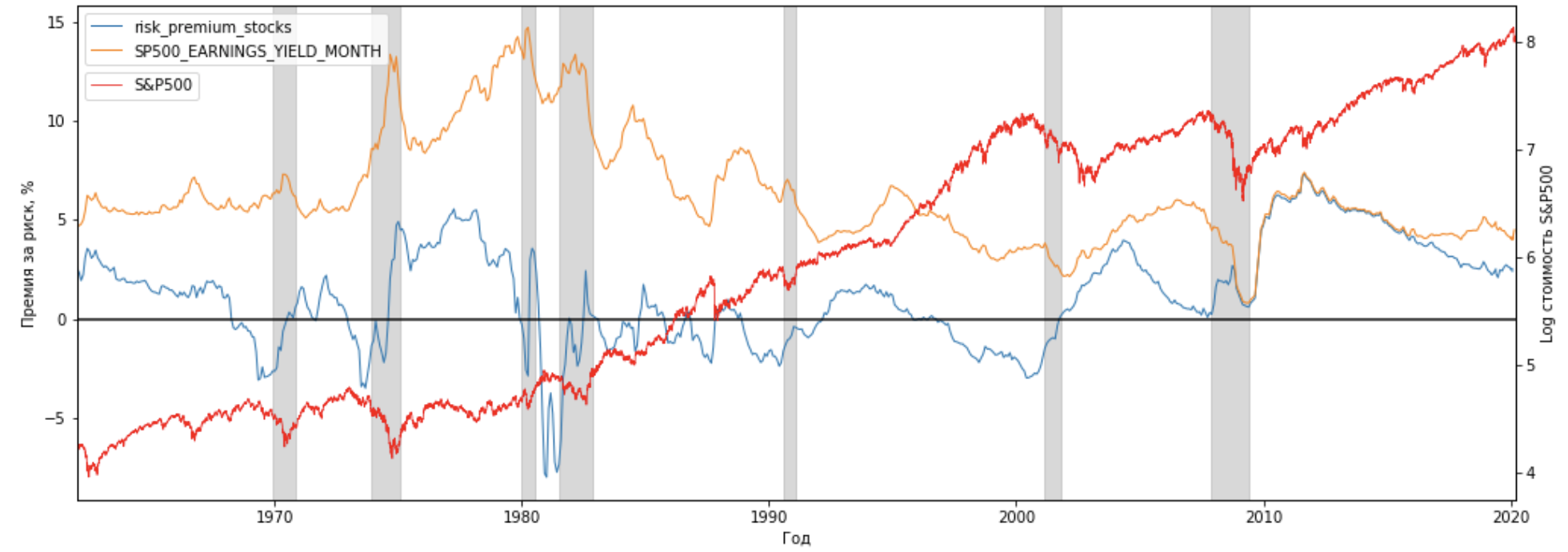
Для облигаций:




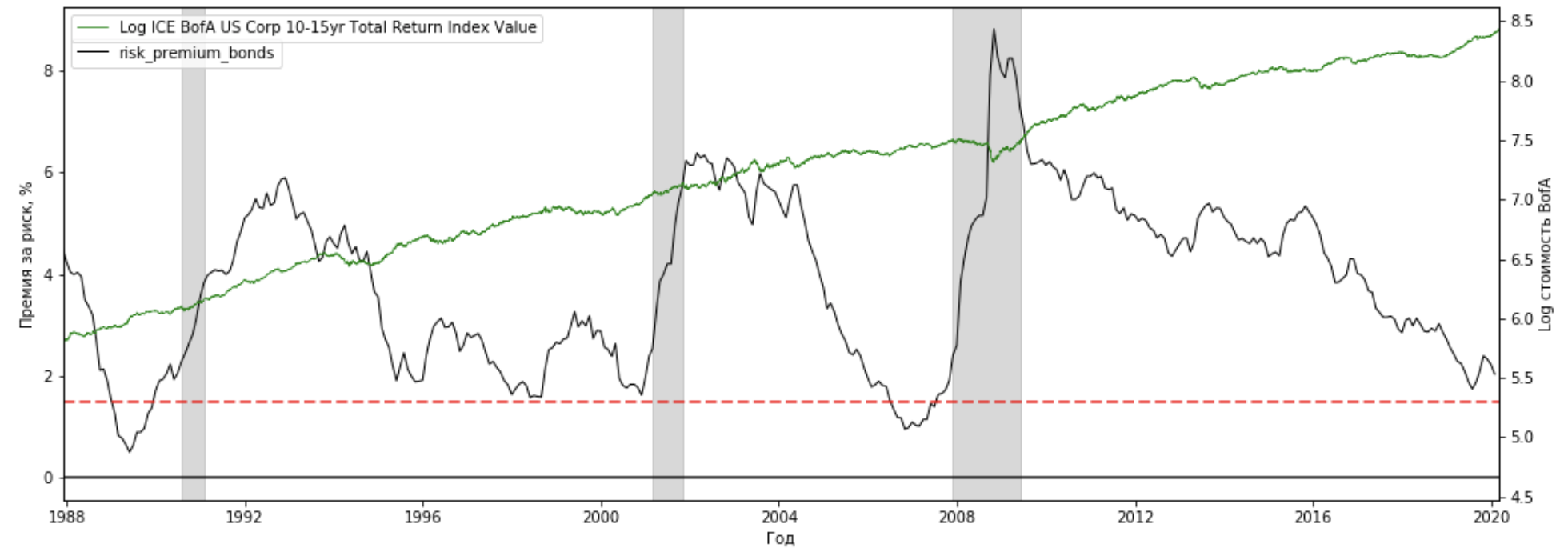
Как мы видим, предкризисные периоды это зоны с отрицательной премией за риск для акций и сниженной премией за риск для облигаций.

При этом для облигаций не всегда сниженная премия за риск это сигнал к началу кризиса на рынке облигаций (снижение индекса BofА произошло только в 2008 году), но вот сниженная премия на рынке акций почти всегда (кроме периода после кризиса в начале 1980-х, когда продолжительное время держалась отрицательная премия) приводит к снижению стоимости акций.

Что означает отрицательная премия за риск для акций?

Покупая акцию, мы получаем доходность ниже безрисковой ставки на рынке. При этом, принимая на себя в полной мере риски колебания цены акции и потенциальных убытков. Это не стандартная ситуация, инвесторы понимают, что премия за риск не может быть отрицательной, в следствии чего рынки приходят к осознанию того, что текущая стоимость акций слишком высока и начинаются распродажи. Падение усиливается после того, как инвесторы широкого круга (обычные люди, не институциональные инвесторы) начинают поддаваться панике, продавая свои портфели и усугубляя падение. Таким образом, реакция рынков быстрая и сильная.
Стоит заметить, что падение рынка не идет до предыдущего уровня премии за риск, а всегда происходит значительно сильнее, что увеличивает премию за риск значительно и вновь усиливает привлекательность ценных бумаг для инвесторов.

Причем, если посмотреть на премии за риск для акций и облигаций на одном графике, то мы увидим, что премия за риск для облигаций традиционно была выше, чем для акций, однако в последние 5 лет они синхронизировались и обе постепенно стремятся к нулю:




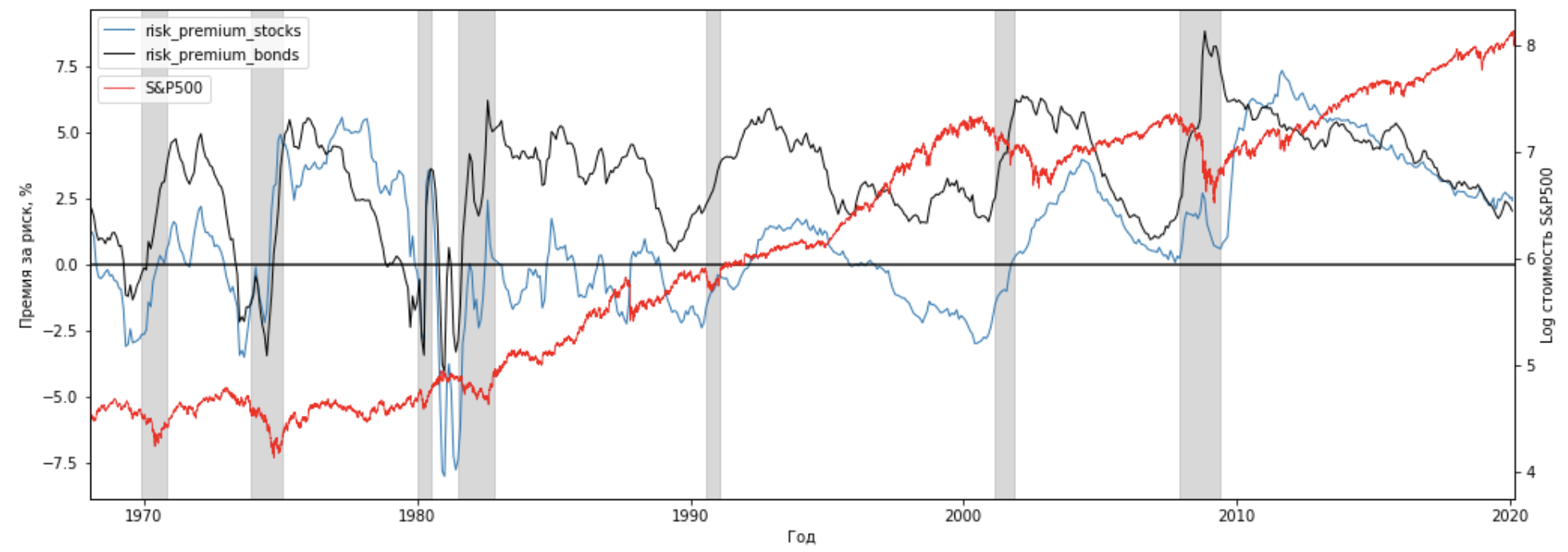
По состоянию на 9 марта 2020 года, не смотря на резкое и сильное падение фондового рынка США, доходности акций все еще далеки от отрицательной зоны, что дает обнадеживающий сигнал.

Спред между доходностями казначейских облигаций

Альтернативным индикатором предкризисной ситуации на рынке является разность между доходностями долгосрочных и краткосрочных казначейских облигаций.

Наименее зашумлённым и наиболее практически полезным является спред между доходностями 10 летних и 2 летних казначейских облигаций:




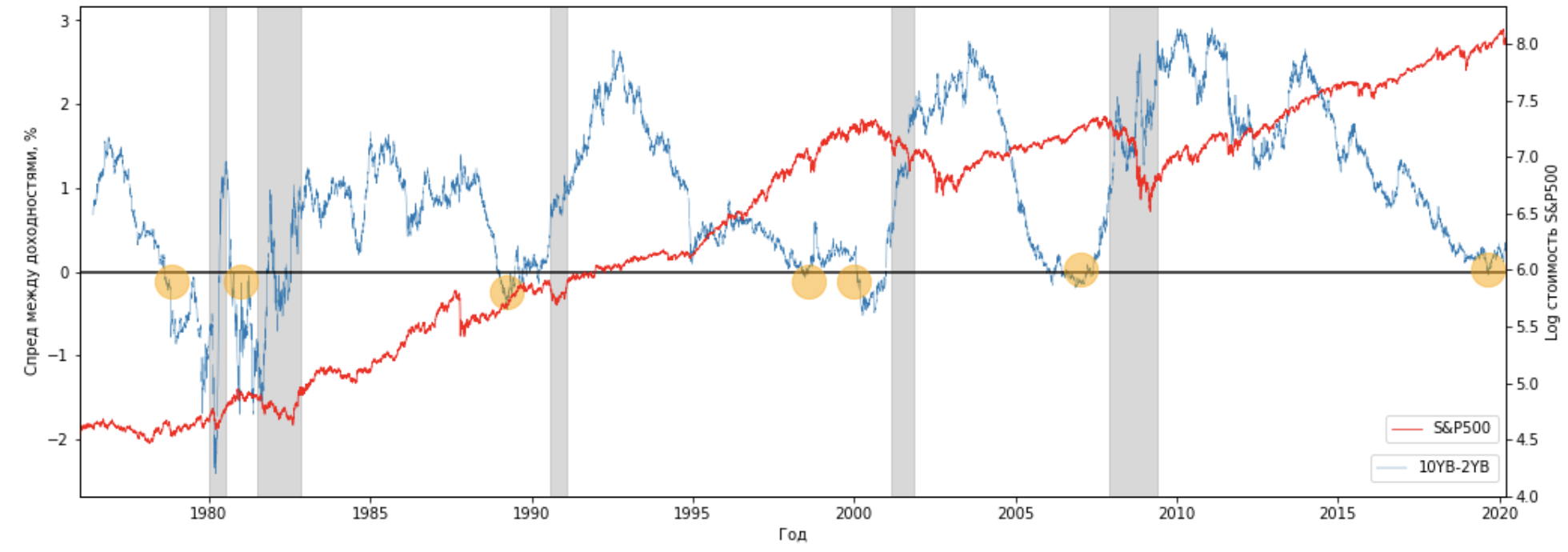
Данный индикатор является наиболее правдивым с исторической точки зрения и предсказал 7 последних финансовых кризисов.

Спред между доходностями облигаций в данном случае отражает настроение инвесторов — если они считают, что в скором времени состояние экономики ухудшится, они начинают перекладывать деньги из краткосрочных облигаций (со сроком погашения 2 года) в долгосрочные инструменты (со сроком погашения 10 лет) с фиксированной доходностью самого надежного эмитента — казначейство США.

Скупка долгосрочных облигаций сказывается на их доходности, так как покупка облигаций на значительные объемы денежных средств приводит к удорожанию стоимости облигации. Когда купон — фиксированная величина, удорожание тела облигации ведет к уменьшению ее доходности.
Для краткосрочных облигаций, которые в данном случае распродают, ситуация обратная — тело начинает дешеветь, в условиях фиксированного купона, соответственно, доходность начинает расти.

Однако FRED не дает информации дальше чем 1976 по данному спреду, поэтому, мы можем для иллюстративных целей взять доходность 10 летних казначейских облигаций минус ставка FED (вместо краткосрочных 2 летних облигаций), чтобы посмотреть, что происходило начиная с 1962 года и охватив еще 2 кризиса:




Не смотря на общую зашумленность данного спреда (сравните со спредом 10 year — 2 year), кризисы 73 и 69 годов также претворялись снижением спреда в отрицательную зону.

Что на текущий момент?
Дела не очень — индикатор уже показывал отрицательную зону в 2019 году.
Институциональные инвесторы ожидают, что в ближайшем будущем нас ожидают серьезные потрясения и из-за этого перекладываются в долгосрочные инструменты с фиксированной доходностью.

Сколько осталось до кризиса?
Как видно из графика спреда, инвертированная доходность предваряет кризисы на год-два.
Учитывая то, что инверсия произошла в конце 2019 года и рынки США уже начали свое падение из-за ожидания будущей рецессии из-за вируса COVID-19, кризис подступает прямо сейчас.

По состоянию на 9 марта 2020, доходность 10 летних облигаций казначейства США снизилась до 0.318% — самое низкое значение за всю историю наблюдений!
Кажется нас ждет что то большое и это уже началось.

текущее значение T10YFF: -0.17
текущее значение T10Y2Y: 0.25

Прошлые цены никак не дают предсказать кризис

Для примера беспомощности технического анализа в данном вопросе возьмем индикатор RSI.
RSI — relative strength index в теории показывает «перекупленность» и «перепроданность» рынка.
Перекупленность рынка — это и есть состояние, когда цены должны скорректировать вниз, то есть, кризис на фондовом рынке.

Ссылка на Вики с описанием индикатора

Мы можем посчитать этот индикатор с помощью Питона, для расчета возьмем период — 244 торговые сессии (1 календарный год):

SP500_returns = GSPC_h['Close'].pct_change()
delta = GSPC_h['Close'].diff()
window_length = 500

# Make the positive gains (up) and negative gains (down) Series
up, down = delta.copy(), delta.copy()
up[up < 0] = 0
down[down > 0] = 0

# Calculate the EWMA
roll_up1 = up.ewm(span=window_length).mean()
roll_down1 = down.abs().ewm(span=window_length).mean()

# Calculate the RSI based on EWMA
RS1 = roll_up1 / roll_down1
RSI1 = 100.0 - (100.0 / (1.0 + RS1))

Что мы видим на графике RSI?

Множество зон «перекупленности», что могло бы сигнализировать о слишком сильно выросшем рынке, которому пора скорректироваться вниз. Но он продолжал идти вверх (например длительный период с 1995 года индикатор показывает «перекупленность», но перед началом кризиса 2001 года он возвращается в свою обычную зону и не сигнализирует о «перекупленности», что, однако, заканчивается кризисом).

Иными словами, применение осцилляторов для предсказания кризиса — весьма спорное занятие.

Перед кризисами рынок растет плавно, не показывая высокой волатильности «вверх», в отличии от падений — они всегда резкие и стремительные. Это мы видим как раз около нижней границы осциллятора — ее пересечение практически всегда точно показывало, когда кризис пришел и «дно» падения близко. Сигнал на покупку?

Выводы

На данный момент ситуация выглядит настораживающее, есть прямые индикаторы, показывающие возможное наступление рецессии. Помимо рассмотренных, существует еще индекс промышленного производства (является опережающим для экономических (не финансовых!) кризисов). Можно было бы также углубиться в макроэкономическую статистику и добавить к анализу показатели платежного баланса, ВВП и тому подобные, однако, за нас это все уже сделали институциональные инвесторы — их реакция отражена в спреде доходностей долгосрочных и краткосрочных облигаций. Осталось расслабиться и наблюдать за шоу, если у Вас нет финансовых вложений. А если есть — подумать о возможном хеджировании своих позиций или выходе в кэш до лучших времен.