Число пи и случайность цифр после запятой

14 марта в день «3.14» число пи празднует свой день

Важность темы: исследование распределения цифр пи и цифр иррациональных чисел
открывает возможности исследования непрерывных данных в реальном времени,
когда поступающие данные учитываются без пауз на отдельный ввод массива данных

Пробел Просвещения России и СНГ и СССР:
не изучаем логарифм и интеграл в младших классах
и впоследствии считают простейшее якобы трудным

Вдобавок алгоритмы быстрых вычислений в школе не изучаются,
хотя алгоритмы понятны на многих языках программирования
без применения квантовых компьютеров





Понимая паттерны распределений человеческих и натуральных и машинных и фальшивых
реально применять результаты 4-х видов исследований:

1. Создание случайности
2. Преодоление случайности
3. Фальсификация случайности
4. Преодоление фальсификации случайности

Данная тема освещает общедоступный пирамидальный
спектрально интегральный биномиально логарифмический критерий

Используя 55000 цифр числа пи после запятой,
сначала в программе совместимой с Word заменой специальных символов
цифры переведены в столбик и далее в программе совместимой с Excel
цифры разделены на двоичные признаки: малые \ большие и чётные \ нечётные

Результаты: среднее у обоих двоичных распределений: около 0,5
и разделения на двоичные соответствуют вероятности теоретической

Применяется таблица:




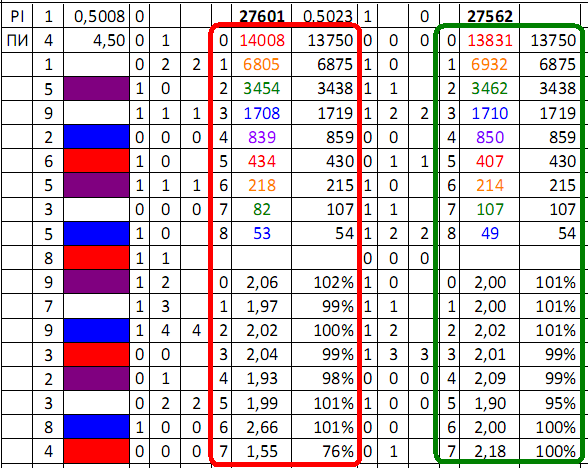
В таблице возможно программировать другие функции контроля
В таблице возможно создавать графики значений любых ячеек

Продолжение таблицы исследует случайные перестановки последовательности



Предварительные выводы: обнаруживается преобладание спектра повторяющихся признаков,
что свойственно для последовательностей природных, например, набрав вручную
3000 цифр, 1-й спектр повторяющихся признаков окажется превышающим теоретическое значение

Используя возможности таблицы для перестановки элементов последовательности и перетасовав,
спектры принимают значения теоретические как были бы синтезированы ГПСЧ и КСГПСЧ

Спектры подчиняются формуле Данилиных: N = LOG(1-c)/LOG(1-p) по принципу:
при С=P=0,5; N = 1 = log0,5/log0,5 = log(1-1/2)/log(1-1/2) = 1
при C=0,25; P=0,5; N = 2 = log0,75/log0,5 = log(1-1/4)/log(1-1/2) = 2 и т.д.


Программа распределения случайных на спектры
количества подряд одинаковых признаков
меньше \ больше и чётный \ нечётный

Практические распределения соответствуют теоретическим
значит случайная последовательность качественная
и возможно изучить паттерны различных последовательностей

Биномиальное Логарифмическое Интегральное Пирамидальное распределение
БЛИП распределение случайных чисел
Binomial Logarithmic Integral Pyramidal Distribution
BLIP distribution of Random numbers

'dablip.bas

RANDOMIZE TIMER
tb = TIMER: s = 0
OPEN "dablip.txt" FOR OUTPUT AS #2
n = VAL(MID$(TIME$, 7, 2))*10 ^ 5
DIM b(n), d(n), e(n), f(n)
DIM j(n), k(n), m(n), p(16), q(16)
LOCATE 1, 1: PRINT " THEORY Average BIG EVEN "

FOR i = 2 TO n-1
 b(i) = INT(RND*900)+100: s = s+b(i): m = s/i

 IF b(i) < m THEN d(i) = 0 ELSE d(i) = 1
 IF (b(i) MOD 2) = 0 THEN j(i) = 0 ELSE j(i) = 1

 IF d(i) = d(i-1) THEN e(i) = e(i-1)+1 ELSE e(i) = 0
 IF e(i) = 0 THEN f(i) = e(i-1) ELSE f(i) = 12
 IF f(i) > 12 THEN f(i) = 12

 IF j(i) = j(i-1) THEN k(i) = k(i-1)+1 ELSE k(i) = 0
 IF k(i) = 0 THEN m(i) = k(i-1) ELSE m(i) = 12
 IF m(i) > 12 THEN m(i) = 12

 p(f(i)) = p(f(i))+1: q(m(i)) = q(m(i))+1

 IF (i MOD 1000) = 0 THEN LOCATE 3, 1: PRINT i, " from ", n, INT(100*i/n); " %",
NEXT

LOCATE 3, 1: FOR t = 1 TO 12
 PRINT INT(n/(2^(t+1))), INT((p(t-1)+q(t-1))/2), p(t-1), q(t-1)
NEXT

te = TIMER
PRINT: PRINT te-tb; "second", INT(n/(te-tb)); " in second "
PRINT n, " elements ",

PRINT #2, te-tb; "second", INT(n/(te-tb)); " in second "
PRINT #2, n, " elements ",: PRINT #2,

PRINT #2,: PRINT #2, " THEORY Average BIG EVEN ": PRINT #2,
FOR t = 1 TO 12
 PRINT #2, INT(n/(2^(t+1))), INT((p(t-1)+q(t-1))/2), p(t-1), q(t-1)
NEXT

Особенность программы: индексы индексов p(f(i)) & q(m(i))

Думаю у случайных проблемы с чётностью:
слишком резко меняется чётность случайных

Результаты:

40 second 139'555 in second 
 5'600'000 elements 

 	THEORY	Average	BIG	EVEN

	1400000	1400610	1399595	1401625
	700000	700026	700122	699931
	350000	349716	349508	349925
	175000	174823	174892	174755
	87500	87424	87564	87285
	43750	43837	43931	43744
	21875	22028	21983	22074
	10937	10850	10865	10835
	5468	5481	5496	5466
	2734	2755	2732	2778
	1367	1388	1396	1380
	687	687	687	687

Для самостоятельного изучения:

1. Равномерность каждой из цифр числа пи
1. Методы примерного вычисления числа пи
1. Выучить 8 цифр числа пи после запятой
1. Найти формулы вычисления цифр числа пи
1. Вспомнить формулы длины окружности