28.03.2020 09:07
rahmaevao 11 4200 Источник

Coderik однажды отметил: "Фильтра Калмана много не бывает". Так же можно сказать и о теореме Байеса, ведь это с одной стороны так просто, но с другой стороны так сложно осмыслить его глубину.



На просторах YouTube есть замечательный канал Student Dave, однако последнее видео опубликовано шесть лет назад. На канале представлены обучающие видео, в которых автор рассказывает очень простым языком сложные вещи: теорему Байеса, фильтр Калмана и пр. Свой рассказ студент Дейв дополняет примером расчета в matlab.


Однажды мне очень помог его видео урок под названием “Итеративная байесовская оценка” (на канале ему соответствует плейлист “Iterative bayesian estimation: with MATLAB”). Я захотел, чтобы каждый мог познакомиться с объяснениями Дейва, но к сожалению проект не поддерживается. Сам Дейв не выходит на связь. Добавить перевод к видео нельзя, так как это должен инициировать сам автор. Обращение в youtube не дало результата, поэтому я решил описать материал в статье на русском языке и опубликовать там, где его больше всего оценят. Материал очень сильно переработан и дополнен, так как он прошёл через мое субъективное восприятие, поэтому выложить его как перевод было бы неуместно. Но саму соль объяснения я взял у Дейва. Его код я переписал на python, так как я сам в нем работаю и считаю хорошей заменой математическим пакетам.


Итак, если вы хотите глубже осмыслить тему теоремы Байеса, добро пожаловать.


Постановка задачи


Для того чтобы проиллюстрировать мощь теоремы Байеса для непрерывных случайных величин, Дейв предлагает рассмотреть задачу “байесовского ниндзя”. Суть задачи в следующем.



Есть ниндзя-математик, который очень не любит перепелов. Перепел прячется в кустах, а ниндзя сидит на дереве рядом. Ниндзя может одним решительным прыжком на перепела сразить его, но он не знает где точно находится перепел. При этом перепел и издает время от времени звук. По звуку ниндзя может определить местоположение перепела, но очень неточно. Теорема Байеса позволяет ниндзя по серии криков перепела определить местоположение перепела все точнее и точнее. И в какой-то момент количество криков позволит ниндзя нанести сокрушительный удар.


Спойлер

Если вы ознакомитесь с видео на канале, то узнаете, что ниндзя так и не удалось удачно спрыгнуть на перепела, но это уже другая история.


Одномерный случай


Ниндзя-математик видит кусты как ограниченную область по оси $ x $. Истинное положение перепелки $x = 3$ пока неизвестно. Вероятность в каждой точке области поиска одна и та же. Априорное распределение равномерное.



В процессе наблюдения (ниндзя славились своей выдержкой) были получены $ N = 100 $ замеров (гипотез) местонахождения.


К тому же ниндзя замерил дисперсию измерения положения перепелки по крику $\sigma_y^2=4$.
Благодаря теореме Байеса есть возможность из равномерного распределения получить нормальное, да и с дисперсией куда меньшей чем дисперсия измерения.


Теорема Байеса


$$display$$\begin{equation} f_{posterior}(x) = \frac{f_{prior}(x) \cdot f_{изм}(x)}{\int f_{prior}(x) \cdot f_{mes}(x) dx}, \end{equation}$$display$$


где $ f_{posterior}(x) $ — уточненное распределение;
$ f_{prior}(x) $ — распределение известное до опыта;
$ f_{mes}(x) $ — распределение модели измерения (правдоподобие $ L_x(sample) $).
Дисперсия распределения модели измерения известна ниндзя заранее. За математическое ожидание принимается точка пространства, а за случайную величину замер (вероятность гипотезы о том, что в этой точке пространства сидит перепелка при получении замера):


$$display$$\begin{equation} f_{mes}(x) =pdf(x=y, \mu=x, \sigma=\sigma) = \frac{1}{2 \pi \sigma} e^{- \frac{(y-x)^2}{2\sigma^2}}, \end{equation}$$display$$


где $pdf$ — функция плотности нормального распределения;
$\mu$ — математическое ожидание;
$\sigma$ — стандартное отклонение измерения;
$y$ — измеренная величина.
Данную формулу необходимо повторить для серии опытов ($N$), каждый раз подставляя вместо априорного распределение апостериорное, которое было получено при предыдущем опыте.


На анимации ниже видно как меняется распределение от оценки к оценке.



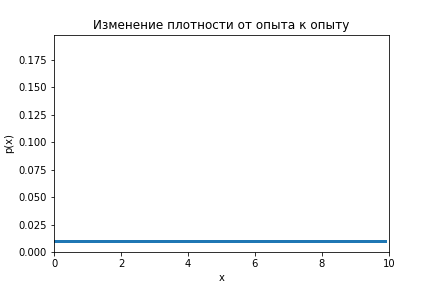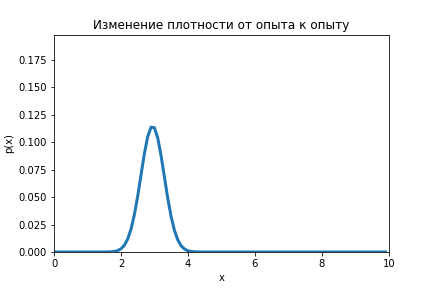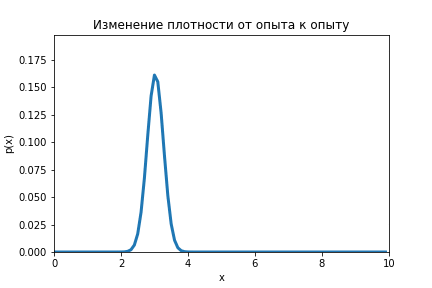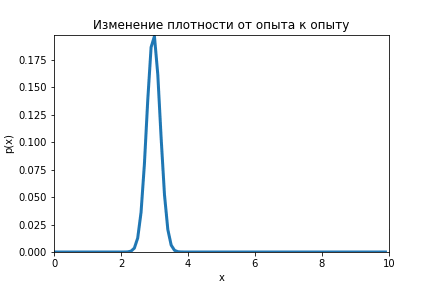
Код по ссылке.
Как только шесть $\sigma$ уменьшатся до размера ноги ниндзя, он сможет нанести свой сокрушительный удар с вероятностью успеха в 99,7 %.


Двумерный случай


Можно не читать

Так-то именно двумерный случай рассмотрен Дейвом, в отличие от одномерного случая.


Рассмотрим более реальную задачу. Ведь ниндзя всё таки смотрит на кусты сверху-вниз.
Истинное положение перепелки $(3, 5)$. Дисперсии (ковариационная матрица) и количество криков те же.

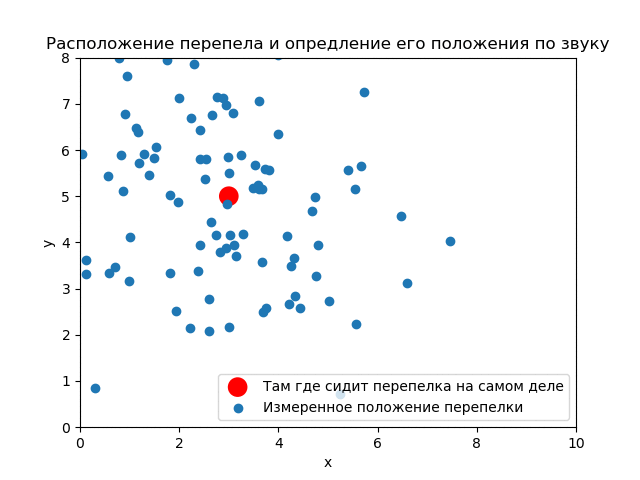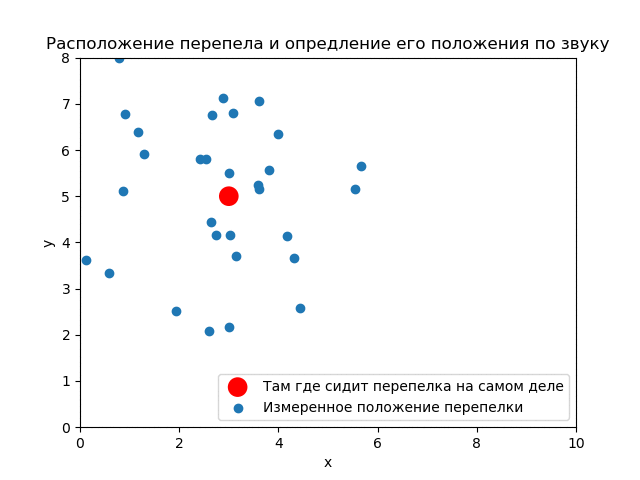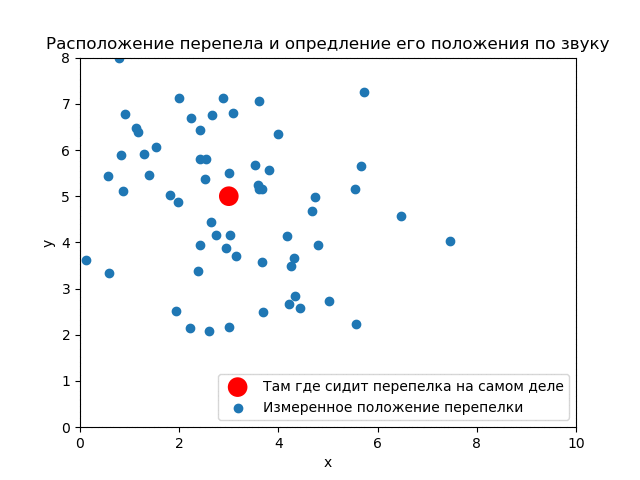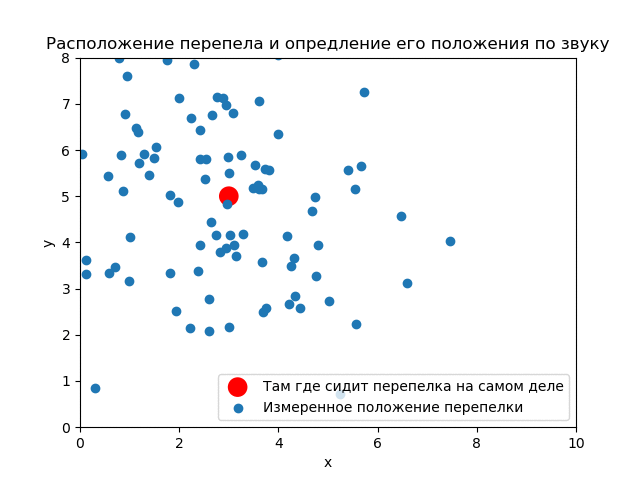
До опыта (априори) вероятность того, что перепелка будет в любом месте кустов одинакова. Априорное распределение равномерное.

Формула Байеса для непрерывных многомерных случайных величин примет вид:


$$display$$\begin{equation} f_{posterior}(X) = \frac{f_{prior}(X) \cdot f_{изм}(X)}{\int f_{prior}(X) \cdot f_{mes}(X) dX}, \end{equation}$$display$$


где $ X $ — вектор координат вида $\begin{pmatrix} x\\ y\end{pmatrix}$;
$ f_{posterior}(X) $ — уточненное распределение;
$ f_{prior}(X) $ — распределение известное до опыта;
$ f_{mes}(X) $ — распределение модели измерения.
Распределение модели измерения:


$$display$$\begin{equation} f_{mes}(X) = \frac{1}{(2\pi)^2 detK} e^{ \frac {1}{2} (Y-X)^T K^{-1} (Y-X)}, \end{equation}$$display$$


где $K$ — ковариационная матрица;
$Y$ — результат замера вида $\begin{pmatrix} x\\ y\end{pmatrix}$.
На анимации ниже видно, как меняется распределение от опыта к опыту.

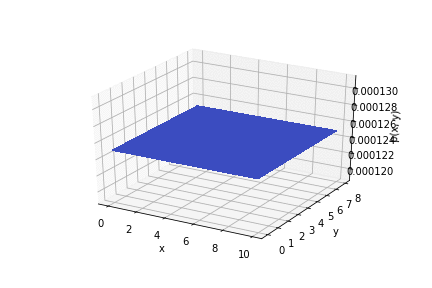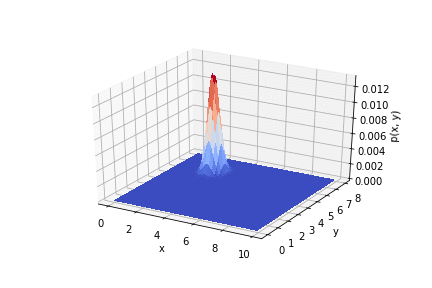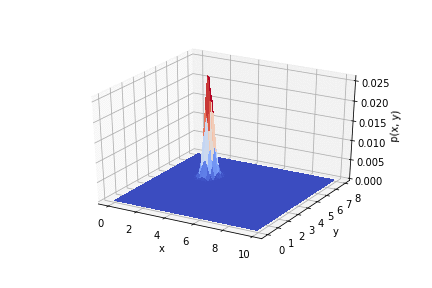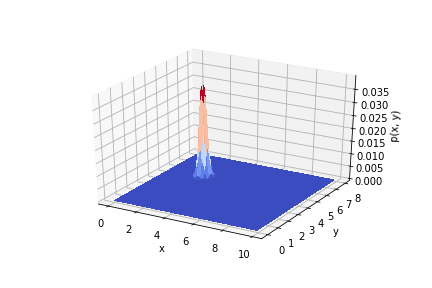
Код по ссылке.


Вывод


Таким образом видно, как результаты опыта влияют на априорное распределение.


Теорема Байеса очень необычная. Ты вроде её понял, но она не устает удивлять тебя своими применениями.


Заходите на канал Дейва в течении этих недель самоизоляции. Всем добра.