В трёх частях этой статьи мы:

• Напишем нейросеть с нуля на Python и обучим её алгоритмом градиентного спуска.
• Применим её к датасету The Wisconsin Cancer Data-set и предскажем по 9 различным признакам, является ли опухоль доброкачественной или злокачественной.
• Подробнее исследуем, как работает градиентный спуск и метод обратного распространения ошибки.
• Рассмотрим основы и изучим более сложные идеи. В части 1 мы разберёмся с архитектурой нашей нейросети, в части 2 напишем её на Python и глубже посмотрим на обратное распространение и градиентный спуск, а в части 3 применим её к The Wisconsin Cancer Data-set.

Вступление

Сегодня восхитительное время для всех увлечённых тайнами и возможностями глубокого обучения.

Многие герои глубокого обучения делятся своим опытом в своих видео и статьях. Это Jeremy Howard из fast.ai, Andrew Ng из Coursera, Andrej Karpathy, Yann Lecun, Ian Goodfellow, Yoshua Bengio, Lex Fridman, Geoffrey Hinton, Jurgen Schmidhuber и многие другие

Большинство из них рекомендует одну важную идею — постигать основные принципы глубокого обучения, реализуя их самостоятельно.

Сегодня в нашем распоряжении есть прекрасные мощные библиотеки: Tenser?ow, PyTorch, Fast.ai, Keras, Mxnett, Nctk, DL4J и многие другие. Но используя только их, вы можете упустить кое-что важное — возможность глубже поразмышлять о самых важных моментах процесса обучения.
Программирование сети своими силами столкнет вас лицом к лицу с ключевыми проблемами и препятствиями в этом увлекательном приключении и познакомит со скрытыми чудесами глубокого обучения.

Мы рассмотрим все модные архитектуры и последние разработки в глубоком обучении — свёрточные сети, рекуррентные сети, генеративно-состязательные сети и многое другие. Что действительно интересно, практически за каждым успехом в этой области нам будут встречаться одни и те же старые друзья: обратное распространение и градиентный спуск.


Движение по ландшафту функции потерь. Значения масштабированы для наглядности.

Обе эти концепции дают практически безграничные возможности — и далее вы сможете работать с вышеперечисленными библиотеками более свободно и уверенно и будете готовы самостоятельно размышлять над тем, как их улучшить.

Ну что ж, поехали!

В поисках загадочной функции

Многое из происходящего во Вселенной может быть выражено с помощью функции. Функция — это математическая конструкция, которая берет какие-то данные на вход и вычисляет какие-то данные на выход. Причина и следствие. Вход и выход.
Когда мы смотрим на мир, мы видим информацию, мы видим данные. И многое можем из них узнать.

Есть много видов обучения, которое можно производить с этими данными. Давайте взглянем на 3 наиболее распространенных:

• Обучение с учителем (supervised learning). Это тип обучения, при котором мы обучаем нашу загадочную функцию с помощью набора тренировочных данных. Набора пар, которые соединяют входы с соответствующими им правильными выходами.
• Обучение без учителя (unsupervised learning). Это тип обучения, при котором мы обучаем нашу функцию с помощью данных, которые не помечены или не классифицированы каким-либо образом.
• Обучение с подкреплением (reinforcement learning). При этом типе мы обучаем функцию, максимизируя награду получаемую агентом. Агент выполняет действия внутри какой-то среды.

В этой статье мы сосредоточимся на обучении с учителем — области, где глубокое обучение развивается наиболее успешно.

Итак, у нас есть некоторые данные, мы их передаём на вход функции, и также есть выходные данные, которые им соответствуют. И мы хотим понять, как наша загадочная функция связывает выходные данные с входными.

Дело в том, что когда связь между ними достаточно сложна, найти эту функцию становится действительно сложно. И здесь в дело вступают нейронные сети и глубокое обучение.



В своей основе нейронная сеть соединяет ваши входные данные с желаемыми выходными данными через серию промежуточных «весов». Эти веса — просто числа.
С помощью своей архитектуры и алгоритмов оптимизации, которые мы вскоре рассмотрим, нейронные сети становятся универсальными аппроксиматорами. В конечном итоге они могут вычислить любую функцию, соединяющую входы с выходами (при условии, что у нас правильная архитектура и параметры — более подробно см. универсальная теорема аппроксимации — математическая теория нейросетей).

И лучший способ разобраться в нейронных сетях это… создать собственную. Причём с нуля, используя Python. Именно этим мы и займёмся, и в процессе рассмотрим множество интересных тем и концепций.

Лучший способ разобраться в нейронных сетях это… создать собственную

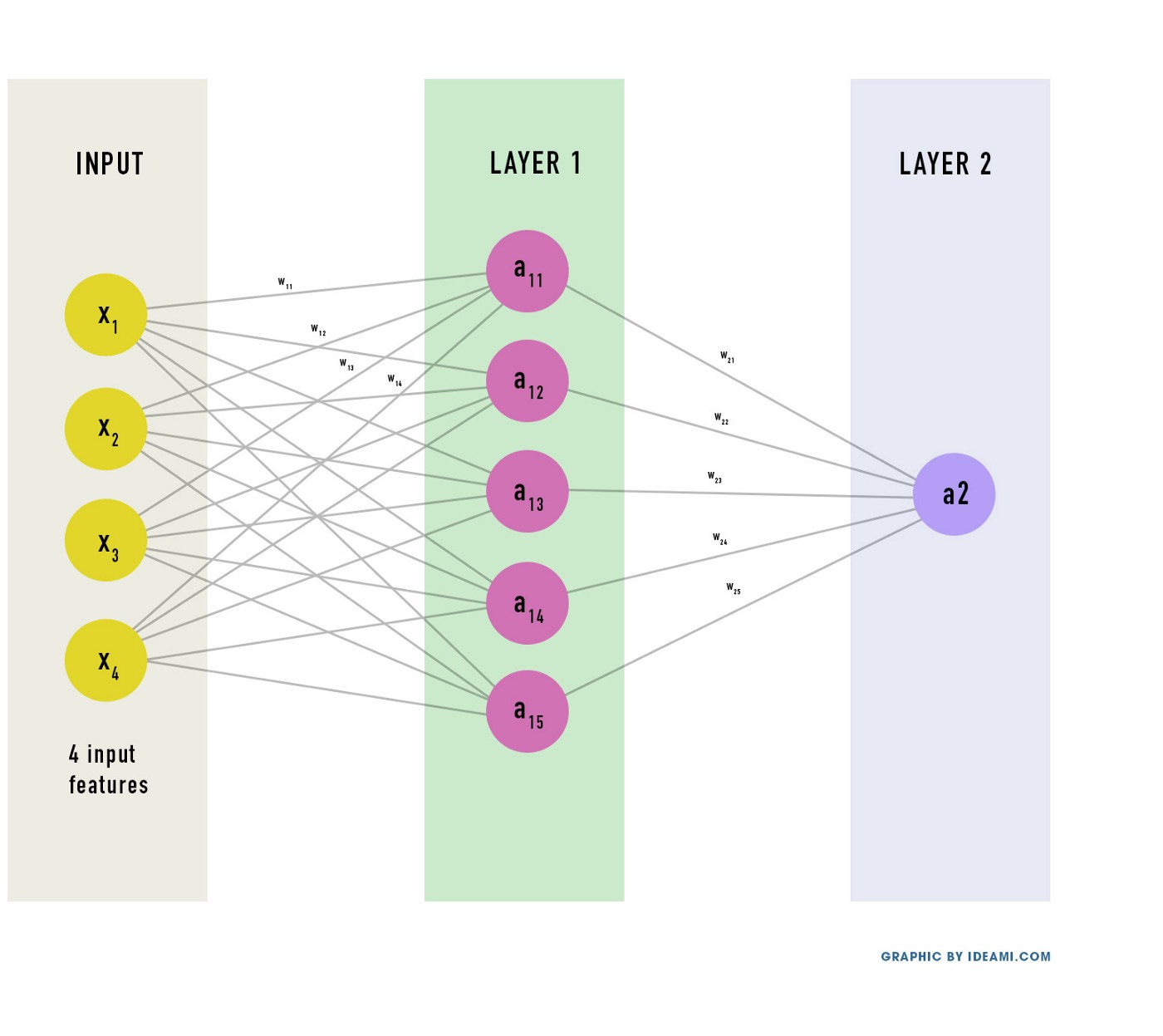
Ниже можно увидеть сеть, которую мы будем строить. У неё 2 слоя (не считаем входной слой).

• Входной слой: содержит исходные данные. Количество нейронов совпадает с количеством признаков. Сеть ниже использует 4 признака. Позже мы будем использовать 9, когда будем работать с датасетом о раке в Висконсине.
• Первый слой: наш первый скрытый слой, он содержит несколько скрытых нейронов. Эти нейроны соединены со всеми нейронами вокруг.
• Второй слой: финальный слой, содержит 1 нейрон — выход сети.

Конечно можно добавить больше слоев и сделать сеть с 10 или 20 слоями, но для простоты мы будем работать с 2 слоями. Двухслойная нейронная сеть, как мы вскоре выясним, может сделать очень многое.Так где же будет происходить обучение сети?
Сначала резюмируем: во входной слой нашей сети мы передаем некоторые данные и показываем, какой выход соответствует этому входу — какой результат должен появиться на выходе сети (на втором слое).

У каждого нейрона сети есть вес (и смещение, но об этом позже). Эти веса — просто числа, которые в начале обучения обычно заполняются случайными значениями.

Нейронная сеть производит некоторые вычисления с входными данными, используя веса. Их результат проходит через сеть до тех пор, пока не получится окончательный результат на выходе.

Результат этих вычислений выражается функцией, которая как бы переводит входы в выходы.

Теперь мы хотим, чтобы сеть узнала наилучшие значения этих весов. Поскольку сеть выполняет вычисления с этими весами на разных слоях, она может аппроксимировать различные виды функции.

Теперь давайте лучше поймем эту загадочную функцию, которую мы ищем. Для этого очень важно разобраться с обозначениями всех переменных, вовлечённых в нашу миссию.

• Х — входной слой, данные, которые мы передаем нашей сети.
• Y — выходной слой, который соответствует входу Х. Результат, который мы должны получить в конце работы сети.
• Yh — наше предсказание, результат, который мы получим, после того, как передадим Х сети. Следовательно, Y — идеальный выход, Yh — выход, который сеть произвела после того, как мы передали ей наши данные.
• W — веса слоев сети (сумма весов каждой связи).

Начнем с того, что первый слой, наш скрытый слой, производит такие вычисления: W?X.



Сеть вычисляет взвешенную сумму:

• Каждый нейрон в текущем слое соединен с каждым нейроном в предыдущем слое.
• У каждой такой связи есть вес.
• Новое значение каждого нейрона в текущем слое равно сумме результатов умножения значения каждого предыдущего нейрона на вес связи между предыдущим нейроном и текущим нейроном.

В некотором смысле веса выражают, насколько сильны или слабы соединения, силу связи между разными нейронами сети.

А теперь добавим дополнительное слагаемое к этому произведению — коэффициент смещения: W?X + b.

Коэффициент смещения делает нашу сеть более гибкой. Он позволяет «сдвигать» линейные вычисления нейронов, увеличивая тем самым потенциал сети изучать эти загадочных функций быстрее.

• b — коэффициент смещения нейронов.

И вот что получилось: W?X + b. Это называется линейным уравнением. Линейное — потому что оно с помощью умножения и суммы представляет собой линейное отношение между входом и выходом (это отношение может быть выражено линией).

А теперь вспомним, что нейронная сеть может иметь много слоев. В нашем примере их 2, но могло бы быть 20 или 200.

Поэтому мы будем помечать числами, к какому слою какое выражение относится. Линейное уравнение, которые определяет вычисления нашего скрытого слоя (слоя 1): W1?X + b1.

Давайте дадим обозначение результату этого вычисления:

• Z — представляет результат вычисления слоя.

Следовательно, Z1 = W1?X + b1.

Обратите внимание, что это нужно вычислить для каждого нейрона каждого слоя. В нашей сети мы будем использовать векторную реализацию — то есть, будем использовать матрицы для объединения всех вычислений в одну операцию.

Для этой статьи не так важно понимать матрицы на действительно хорошем уровне, но если вы хотите освежить свои знания, можно посмотреть замечательные видео от «3Blue1Brown» и его курс «Сущность линейной алгебры» (примечание: мы переводим этот курс, можно подписаться на канал или в вк).

Пока неплохо. А теперь давайте представим сеть со множеством слоёв. Каждый слой производит подобное линейное вычисление. Когда вы объедините все линейные вычисления вместе, сеть сможет вычислять сложные функции.

Однако, есть небольшая проблема…

Слишком линейно, слишком скучно

Мир сложен. Мир — это беспорядок. В жизни взаимосвязь между входными и выходными данными обычно не бывает линейна. Она склонна быть запутанной, нелинейной.

Сложные функции часто нелинейны. И нейронной сети трудно вычислить нелинейное поведение, если её архитектура создана для линейных вычислений. Поэтому нейронные сети добавляют в конец каждого слоя кое-что ещё: функцию активации.

Функция активации — это нелинейная функция, которая вносит нелинейные изменения в выход (результат вычислений) слоя. Она гарантирует, что сеть способна вычислить всевозможные сложные функции, включая очень сильно нелинейные.

Существует множество различных видов функции активации. Кратко рассмотрим 4 основных.

Но сперва, чтобы хорошо их понять, нужно познакомиться с понятием «градиент» (позже мы рассмотрим его подробнее). Градиент функции в точке также называется её производной и выражает скорость изменения значения функции в этой точке.

В каком направлении и как сильно изменяется значение функции в ответ на изменения входной переменной?

Когда градиенты (производные) становятся слишком маленькими, а функция становится более гладкой, это значит, что мы имеем дело с исчезающим градиентом. Как мы позже узнаем, алгоритм обратного распространения, широко используемый в глубоком обучении, настраивает значения весов сети, используя градиент — с его помощью можно понять, как каждый из параметров влияет на выход сети (ведёт ли его изменение к увеличению или уменьшению выхода?).

Исчезающий градиент — это действительно проблема, потому что если градиент в точке становится слишком маленьким или равным нулю, становится очень трудно определить, в каком направлении изменяется выход системы.

Можно также говорить об обратной проблеме: взрывающемся градиенте. Когда значение градиента становится слишком большим, сеть становится очень нестабильной.

У каждой функции активации есть свои плюсы, но все они могут страдать от исчезающих и взрывающихся градиентов.

Давайте быстренько познакомимся с самыми популярными функциями активации.

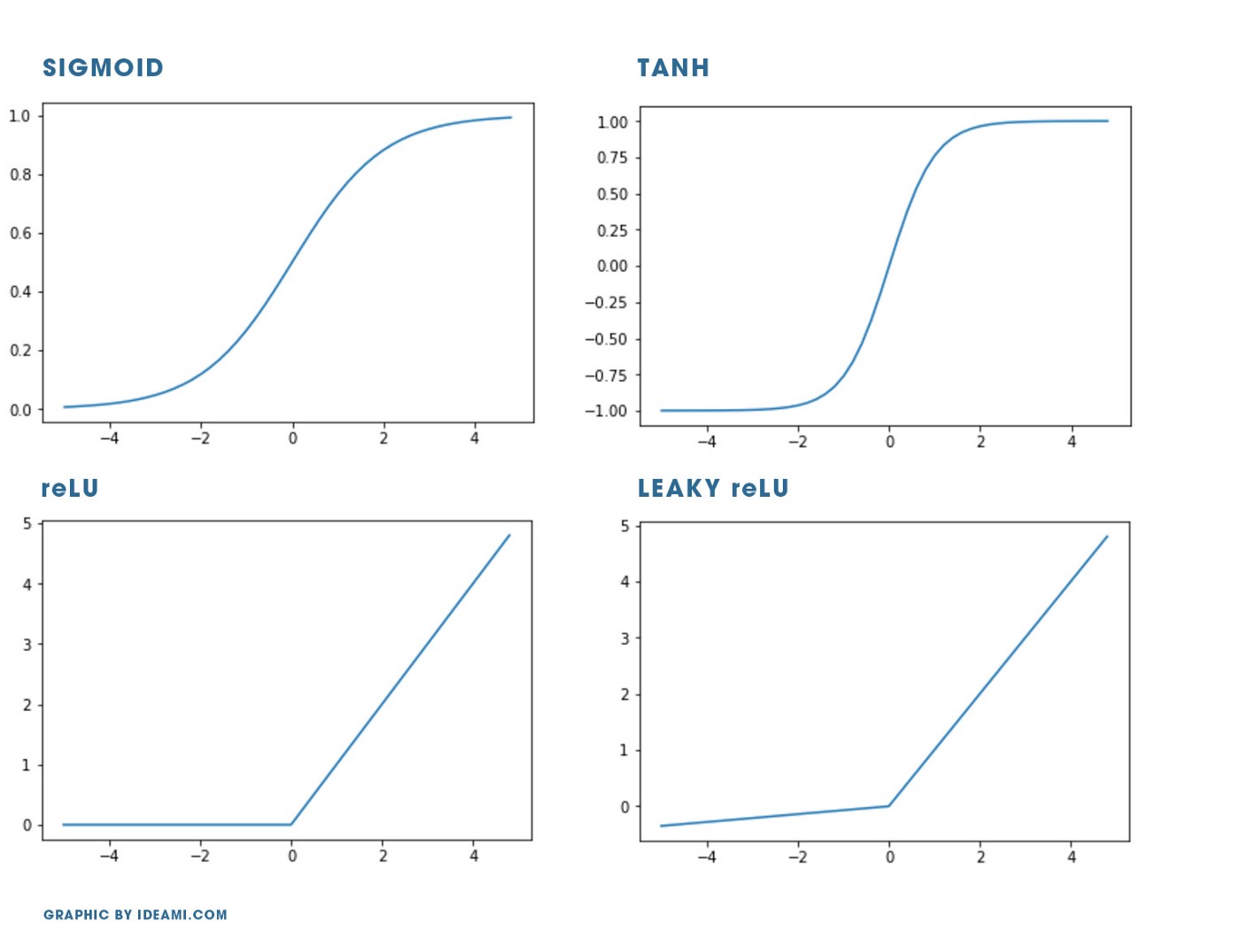
Sigmoid

$$

• Функция принимает значения в диапазоне от 0 до 1.
• Функция нелинейная, она «толкает» аргументы функции к крайним значениям своего диапазона. Это отлично подходит для, например, классификации данных на 2 класса.
• Имеет гладкую форму, так что её градиент будет вполне контролируемым.
• Основной недостаток — что в крайних значениях функция становится совсем «плоской». Это означает, что значение её производной станет очень маленьким, близким к нулю, а эффективность вычислений и скорость нейронов, которые используют эту функцию, может замедлиться или вообще остановиться.
• Сигмоида полезна, когда она является функцией активации нейронов на последнем слое, потому что она приводит выходной сигнал к 0 или 1 (например, классифицируя выходной сигнал на 2 класса). При использовании на предыдущих слоях она подвержена проблемам с исчезающим градиентом.

Tanh (гиперболический тангенс)

$$

• Область значений от -1 до 1.
• Очень похожа на сигмоиду, можно сказать её увеличенная версия.
• Функция имеет более крутую форму, так что ее производная будет «сильнее».
• Минусы такие же, как и у сигмоиды.

ReLU (rectified linear unit)

$$

• Выход равен входу, если входное значение больше 0. В ином случае выход равняется нулю.
• Принимает значения в диапазоне от 0 до бесконечности. Это значит, потенциально выходное значение может быть очень большим. Могут быть проблемы с взрывающимся градиентом.
• Преимущество ReLU в том, что она оставляет сеть более легкой, так как некоторые нейроны могут иметь выходное значение 0, предотвращая тем самым одновременную активность всех нейронов.
• Проблема ReLU в том, что её левая часть абсолютно плоская. Это, как мы уже знаем, означает, что значение её градиента — скорости изменения — будет нулевым, что негативно сказывается на эффективности вычислений.
• Вычислить значение ReLU очень просто, для компьютера это дешёвая операция.
• В настоящее время ReLU — наиболее используемая функция активации на внутренних слоях.

Softmax

$$

• Функция принимает значения в диапазоне от 0 до 1.
• Softmax нормализует вход в распределение вероятностей. Она сжимает входной сигнал в диапазон от 0 до 1, как и сигмоида, но также она ещё и делит результат на сумму всех выходов, поэтому сумма всех выходных сигналов будет равняться 1.
• Обычно эта функция используется на последнем слое, когда нужно сделать классификацию не несколько классов. Softmax будет гарантировать, что значение суммы вероятностей, связанных с каждым классом, всегда будет равняться 1.

В этой статье мы будем использовать Sigmoid на последнем слое и ReLU на скрытом слое.

Окей, мы разобрались с функциями активации, давайте дадим им имена!

• А — представляет выходной сигнал функции активации.

Значит, вычисления, которые мы производим на скрытом слое, примут вид:
A1 = ReLU(Z1)
и Z1=W1?X + b1

А вычисления на выходном слое примут вид:
A2 = Sigmoid(Z2)
и Z2=W2?A1 + b2

Обратите внимание, что мы используем A1 в уравнении для Z2, потому что входным сигналом для нейронов 2 слоя является выходной сигнал нейронов скрытого (предыдущего) слоя.
Также обратите внимание, что Yh = A2. Выход второго слоя — это конечный выход сети.

Это всё. Теперь, если мы объединим все эти вычисления, мы получим полную формулу нашей сети:
Yh = A2 = Sigmoid(W2 ? ReLU ? (W1 ? X+ b1) + b2)

Теперь точно всё. Это всё вычисления, которые производит наша двухслойная нейронная сеть.

То есть, нейронная сеть — цепочка функций, линейных и нелинейных, которые вместе образуют сложную функцию — ту самую загадочную функцию, которая свяжет ваши входные данные с желаемым результатом.

Обратите внимание на переменные W и b в нашей сложной функции. Именно в нахождении их оптимальных значений и заключается обучение. Каким-то образом сеть должна узнать корректные (наиболее оптимальные) значения этих переменные, чтобы правильно вычислить значение функции.
Мы будем учиться находить оптимальные значения для W1, b1, W2, b2. Но перед тем, как мы приступим к тренировке сети, нам нужно инициализировать эти переменные начальными значениями.
Как правильно инициализировать веса и смещения — целая отдельная тема. Для начала мы инициализируем их случайными значениями.

На этом этапе мы уже можем приступить к написанию кода нашей сети. В следующей части мы создадим класс на Python, который будет инициализировать основные параметры сети, и посмотрим, как её тренировать.

Перевод: Титов Дмитрий
Перевод, редактура, корректура, вёрстка: Дмитрий Мирошниченко Keyten

---

Sciberia — это открытый проект, где совместными усилиями участники переводят с английского языка актуальные образовательные и научно-популярные материалы известных мировых институтов и экспертов из различных областей. Участником проекта может стать любой, кто хочет создавать переводы в команде.
Если у вас есть желание помочь с переводами, пишите Станиславу (телеграм: @pieceofchaos).