Object Tracking — очень интересное направление, которое изучается и эволюционирует не первый десяток лет. Сейчас многие разработки в этой области построены на глубоком обучении, которое имеет преимущество над стандартными алгоритмами, так как нейронные сети могут аппроксимировать функции зачастую лучше.
Но как именно работает Object Tracking? Есть множество Deep Learning решений для этой задачи, и сегодня я хочу рассказать о распространенном решении и о математике, которая стоит за ним.
Итак, в этой статье я попробую простыми словами и формулами рассказать про:
Сразу нужно сделать очень важную пометку, которую нужно запомнить — Object Detection это не Object Tracking. Для многих это не будет новостью, но часто люди путают эти понятия. Простыми словами:
Object Detection — это просто определение объектов на картинке/кадре. То есть алгоритм или нейронная сеть определяют объект и записывают его позицию и bounding boxes (параметры прямоугольников вокруг объектов). Пока что речи о других кадрах не идет, и алгоритм работает только с одним.
Пример:
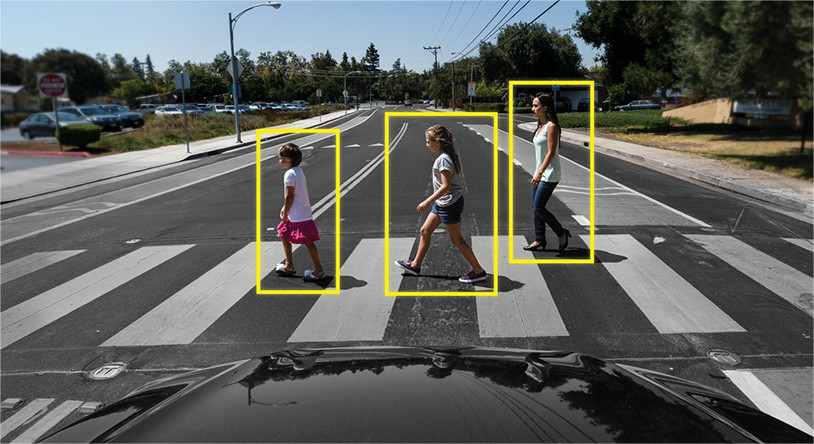
Object Tracking — здесь совсем другое дело. Здесь задача не просто определить объекты на кадре, но еще и связать информацию с предыдущих кадров таким образом, чтобы не терять объект, или сделать его уникальным.
Пример:

То есть Object Tracker включает в себя Object Detection для определения объектов, и другие алгоритмы для понимания какой объект на новом кадре принадлежит какому из предыдущего кадра.
Поэтому Object Detection играет очень важную роль в задаче трэкинга.
Почему YOLO? Да потому что YOLO считается эффективнее многих других алгоритмов для определения объектов. Вот небольшой график для сравнения от создателей YOLO:
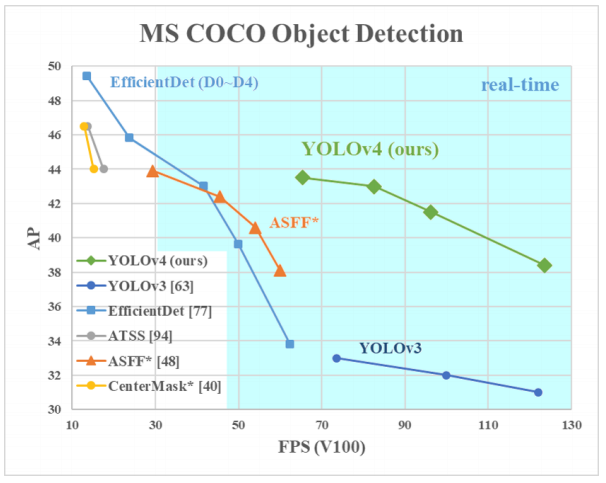
Здесь мы рассматриваем YOLOv3-4, поскольку это самые последние версии и они эффективнее предыдущих.
Итак, существует несколько архитектур нейронных сетей, созданных для определения объектов. Они в основном разделяются на «двухуровневые», такие как RCNN, fast RCNN и faster RCNN, и «одноуровневые», такие как YOLO.
«Двухуровневые» нейронные сети, перечисленные выше, используют так называемые регионы на картинке, чтобы определить, находится ли в этом регионе определенный объект.
Обычно это выглядит так (для faster RCNN, которая является самой быстрой из перечисленных двухуровневых систем):

Но в этих нейронных сетях есть две ключевые проблемы: они не смотрят на картинку «полностью», а только на отдельные регионы, и они относительно медленные.
В чем же крутость YOLO? В том, что эта архитектура не имеет двух проблем свыше, и она доказала неоднократно свою эффективность.
Вообще архитектура YOLO в первых блоках не сильно отличается по «логике блоков» от других детекторов, то есть на вход подается картинка, дальше создаются feature maps с помощью CNN (правда в YOLO используется своя CNN под названием Darknet-53), затем эти feature maps определенным образом анализируются (об этом чуть позже), выдавая на выходе позиции и размеры bounding boxes и классы, которым они принадлежат.

Но что такое Neck, Dense Prediction и Sparse Prediction?
С Sparse Prediction мы разобрались немного ранее — это просто повторение того, как двухуровневые алгоритмы работают: определяют по отдельности регионы и затем классифицируют эти регионы.
Neck (или «шея») — это отдельный блок, который создан для того, чтобы агрегировать информацию от отдельных слоев с предыдущих блоков (как показано на рисунке выше) для увеличения аккуратности предсказания. Если Вас заинтересовало это — можете погуглить термины «Path Aggregation Network», «Spatial Attention Module» и «Spatial Pyramid Pooling».
И, наконец, то, что отличает YOLO от всех других архитектур — блок под названием (на нашей картинке выше) Dense Prediction. На нем мы сфокусируемся чуть сильнее, потому что это очень интересное решение, которое как раз позволило YOLO вырваться в лидеры по эффективности определения объектов.
YOLO (You Only Look Once) несет в себе философию смотреть на картинку один раз, и за этот один просмотр (то есть один прогон картинки через одну нейронную сеть) делать все необходимые определения объектов. Как это происходит?
Итак, на выходе от работы YOLO мы обычно хотим вот это:
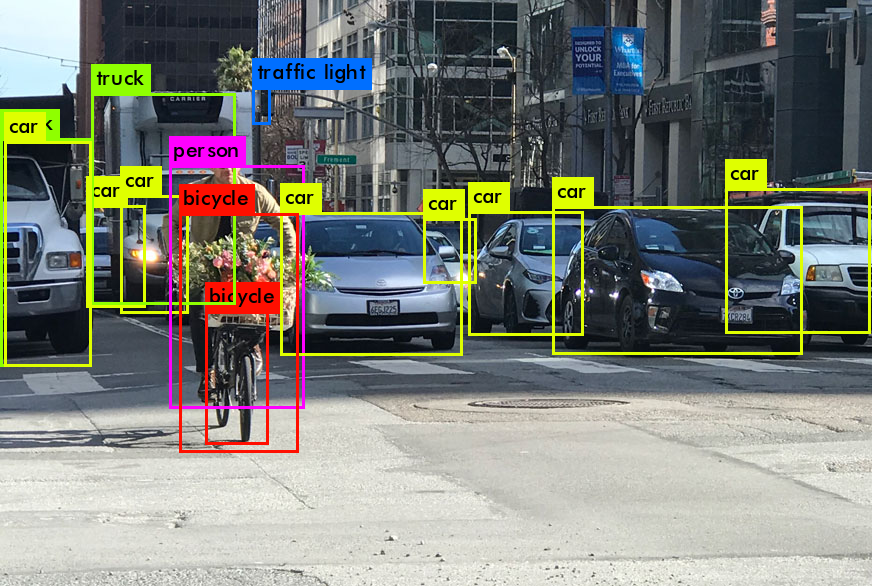
Что делает YOLO когда учится на данных (простыми словами):
Шаг 1: Обычно картинки решейпят под размер 416x416 перед началом обучения нейронной сети, чтобы можно было их подавать батчами (для ускорения обучения).
Шаг 2: Делим картинку (пока что мысленно) на клетки размером axa. В YOLOv3-4 принято делить на клетки размером 13x13 (о различных скейлах поговорим чуть позже, чтобы было понятнее).

Теперь фокусируемся на эти клеточках, на которые мы разделили картинку/кадр. Такие клетки, которые называются grid cells, лежат в основе идеи YOLO. Каждая клетка является «якорем», к которому прикрепляются bounding boxes. То есть вокруг клетки рисуются несколько прямоугольников для определения объекта (поскольку непонятно, какой формы прямоугольник будет наиболее подходящим, их рисуют сразу несколько и разных форм), и их позиции, ширина и высота вычисляются относительно центра этой клетки.
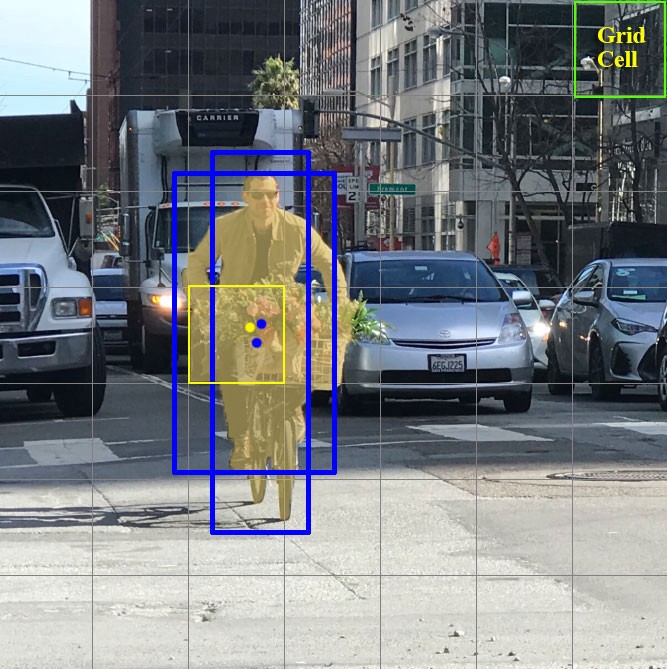
Как же рисуются эти прямоугольники (bounding boxes) вокруг клетки? Как определяется их размер и позиция? Здесь в борьбу вступает техника anchor boxes (в переводе — якорные коробки, или «якорные прямоугольники»). Они задаются в самом начале либо самим пользователем, либо их размеры определяются исходя из размеров bounding boxes, которые есть в датасете, на котором будет тренироваться YOLO (используется K-means clustering и IoU для определения самых подходящих размеров). Обычно задают порядка 3 различных anchor boxes, которые будут нарисованы вокруг (или внутри) одной клетки:

Зачем это сделано? Сейчас все будет понятно, так как мы обсудим то, как YOLO обучается.
Шаг 3. Картинка из датасета прогоняется через нашу нейронную сеть (заметим, что кроме картинки в тренировочном датасете у нас должны быть определенны позиции и размеры настоящих bounding boxes для объектов, которые есть на ней. Это называется «аннотация» и делается это в основном вручную).
Давайте теперь подумаем, что нам нужно получить на выходе.
Для каждой клетки, нам нужно понять две принципиальные вещи:
Какой же должен быть тогда output у YOLO?
1. На выходе для каждой клетки мы хотим получить:

2. Output должен включать в себя вот такие параметры:
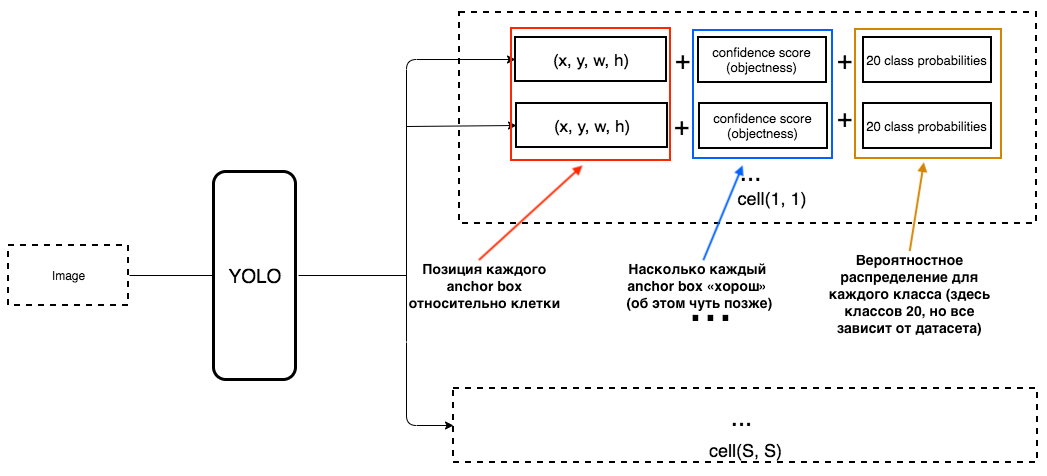
Как определяется objectness? На самом деле этот параметр определяется с помощью метрики IoU во время обучения. Метрика IoU работает так:
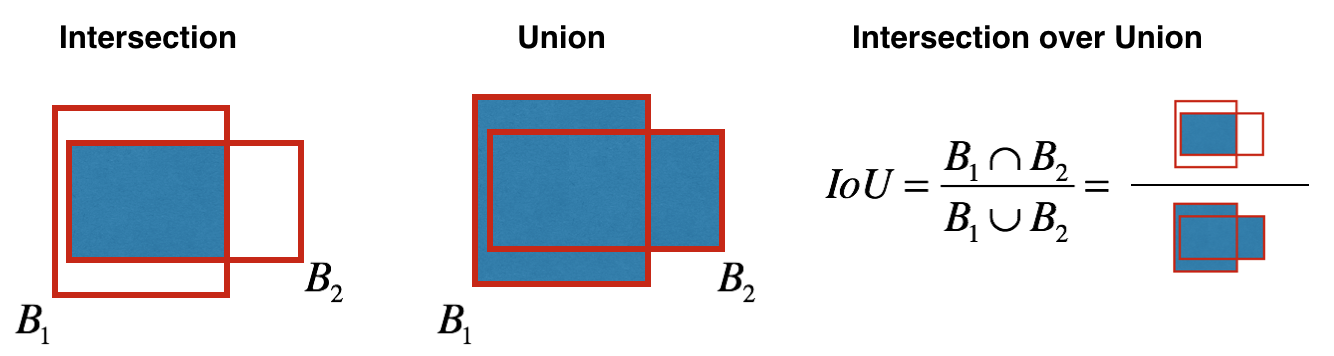
В начале Вы можете выставить порог для этой метрики, и если Ваш предсказанный bounding box будет выше этого порога, то у него будет objectness равной единице, а все остальные bounding boxes, у которых objectness ниже, будут исключены. Эта величина objectness понадобится нам, когда мы будем считать общий confidence score (на сколько мы уверены, что это именно нужный нам объект расположен внутри предсказанного прямоугольника) у каждого определенного объекта.
А теперь начинается самое интересное. Представим, что мы создатели YOLO и нам нужно натренировать ее на то, чтобы распознавать людей на кадре/картинке. Мы подаем картинку из датасета в YOLO, там происходит feature extraction в начале, а в конце у нас получается CNN слой, который рассказывает нам о всех клеточках, на которые мы «разделили» нашу картинку. И если этот слой рассказывает нам «неправду» о клеточках на картинке, то у нас должен быть большой Loss, чтобы потом его уменьшать при подаче в нейронную сеть следующих картинок.
Чтобы было совсем понятно, есть очень простая схема с тем, как YOLO создает этот последний слой:
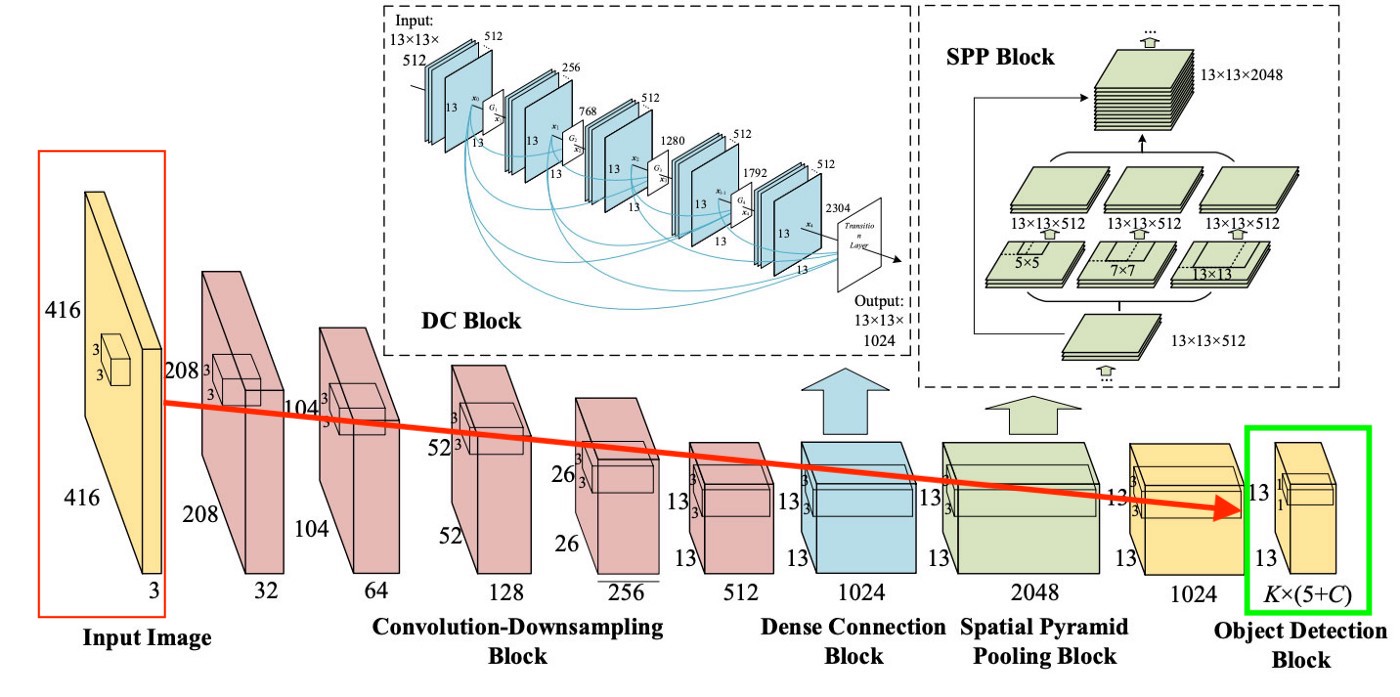
Как мы видим из картинки, этот слой, размером 13x13 (для картинок изначального размера 416x416) для того, чтобы рассказывать про «каждую клетку» на картинке. Из этого последнего слоя и достается информация, которую мы хотим.
YOLO предсказывает 5 параметров (для каждого anchor box для определенной клетки):

Чтобы было легче понять, есть хорошая визуализация на эту тему:

Как можно понять их этой картинки, задача YOLO — максимально точно предсказать эти параметры, чтобы максимально точно определять объект на картинке. А confidence score, который определяется для каждого предсказанного bounding box, является неким фильтром для того, чтобы отсеять совсем неточные предсказания. Для каждого предсказанного bounding box мы умножаем его IoU на вероятность того, что это определенный объект (вероятностное распределение рассчитывается во время обучения нейронной сети), берем лучшую вероятность из всех возможных, и если число после умножения превышает определенный порог, то мы можем оставить этот предсказанный bounding box на картинке.
Дальше, когда у нас остались только предсказанные bounding boxes с высоким confidence score, наши предсказания (если их визуализировать) могут выглядеть примерно вот так:

Мы можем теперь использовать технику NMS (non-max suppression), чтобы отфильтровать bounding boxes таким образом, чтобы для одного объекта был только один предсказанный bounding box.

Нужно также знать, что YOLOv3-4 предсказывают на 3-х разных скейлах. То есть картинка делится на 64 grid cells, на 256 клеток и на 1024 клетки, чтобы также видеть маленькие объекты. Для каждой группы клеток алгоритм повторяет необходимые действия во время предсказания/обучения, которые были описаны сверху.
В YOLOv4 было использовано много техник для увеличения точности модели без сильной потери скорости. Но для самого предсказания оставили Dense Prediction таким же, как и у YOLOv3. Если Вы интересуетесь тем, что же такого магического сделали авторы, чтобы поднять так точность не теряя скорости, есть отличная статья, написанная про YOLOv4.
Надеюсь мне удалось немного донести то, как работает YOLO в целом (точнее последние две версии, то есть YOLOv3 и YOLOv4), и в Вас это пробудит желание воспользоваться этой моделью в будущем, или узнать про ее работу чуть подробнее.
Раз мы разобрались с, пожалуй, лучшей нейронной сетью для Object Detection (если оценивать скорость/качество), давайте наконец перейдем к тому, как же нам связывать информацию о наших определенных YOLO объектов между кадрами видео. Как программа может понимать, что человек на предыдущем кадре — это тот же человек, что и на новом?
Для понимания этой технологии, следует сначала разобраться с парой математических аспектов — расстояние Махалонобиса и фильтр Калмана.
Расстояние Махалонобиса
Рассмотрим очень простой пример, чтобы интуитивно понять, что такое расстояние Махолонобиса и зачем оно нужно. Многим, наверное, известно, что такое евклидово расстояние. Обычно, это расстояние от одной точки до другой в евклидовом пространстве:
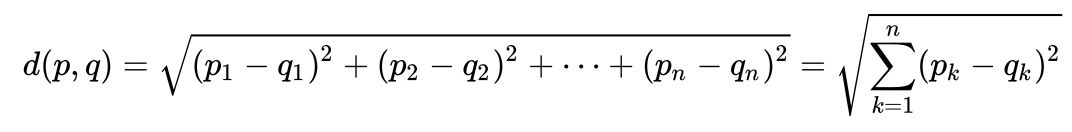

Допустим, у нас есть две переменные — X1 и X2. Для каждой из них у нас есть много измерений.
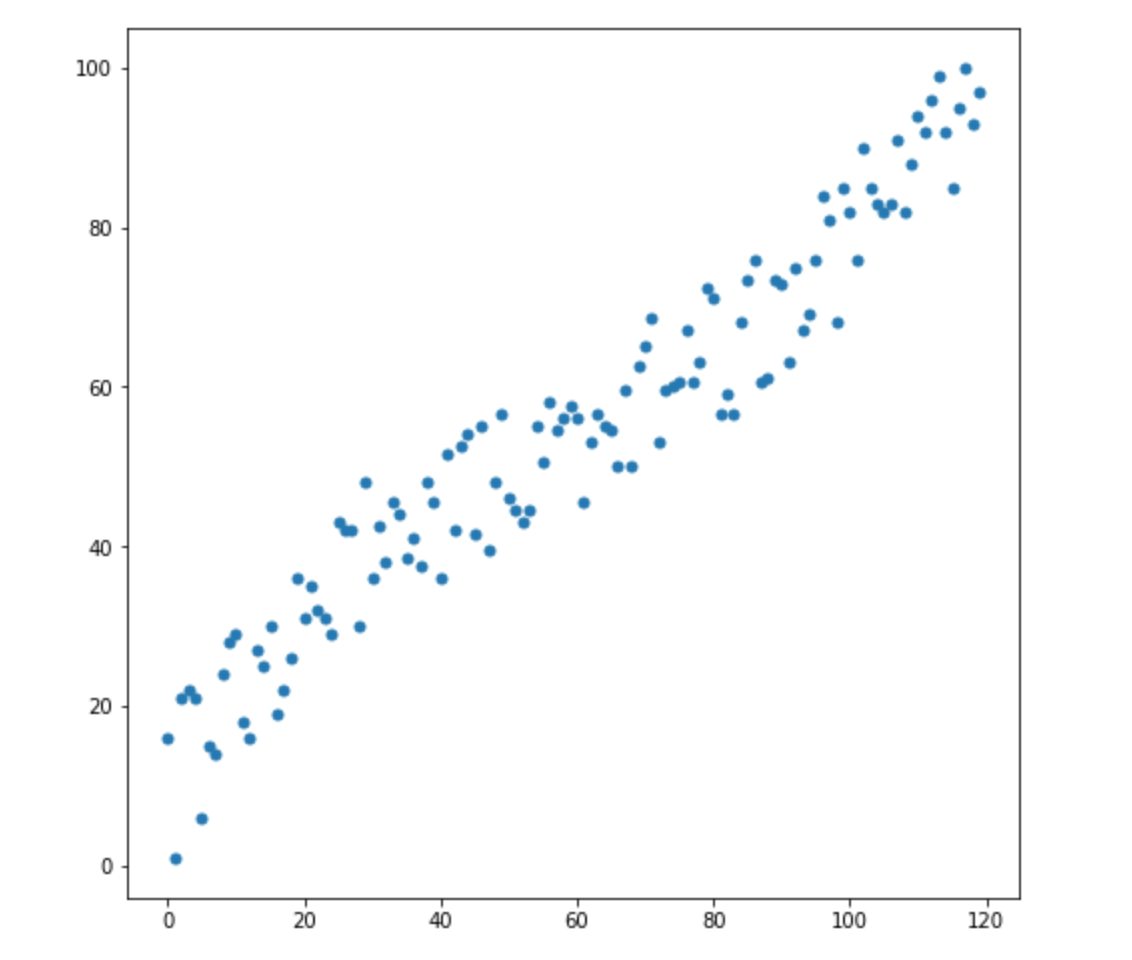
Теперь, допустим, у нас появилось 2 новых измерения:
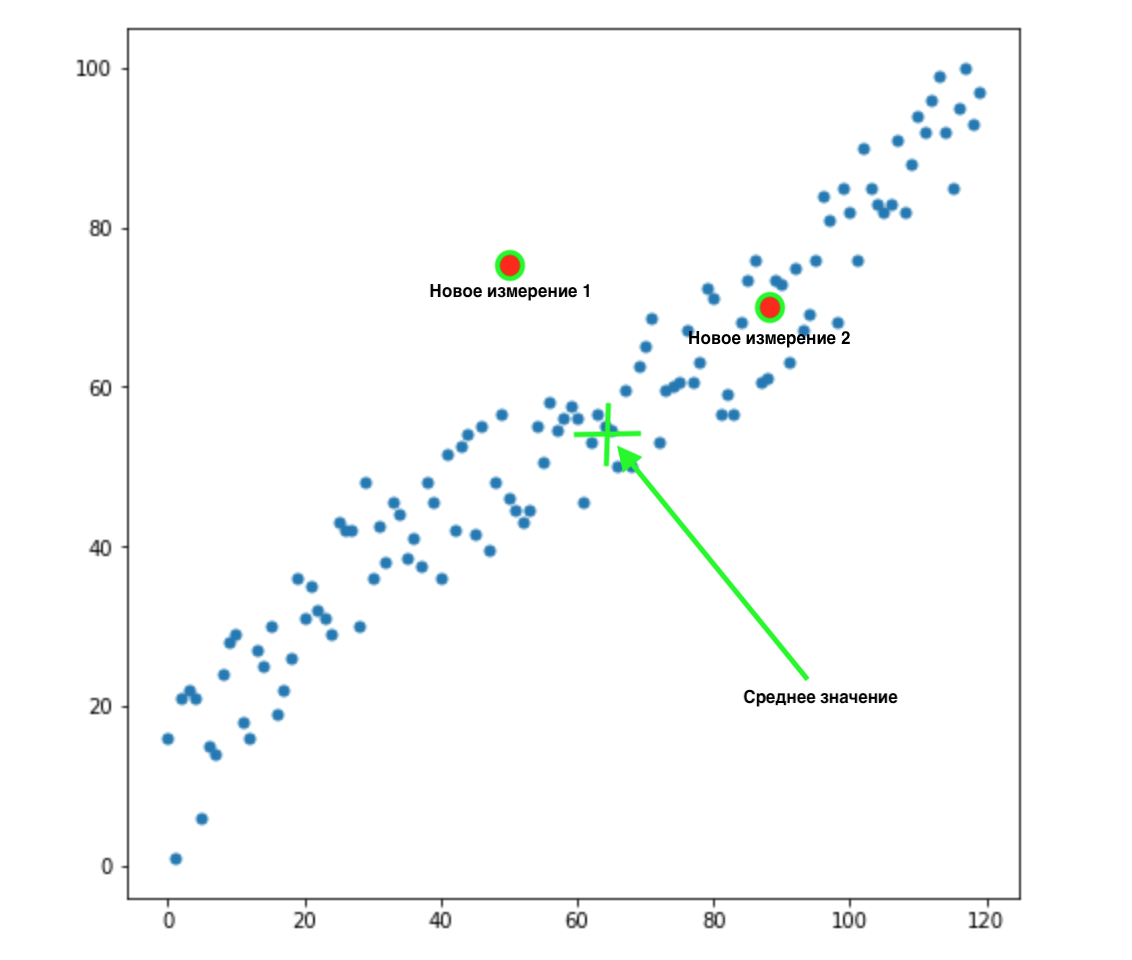
Как понять, какое из этих двух значений наиболее подходит для нашего распределения? На глаз все очевидно — точка 2 нам подходит. Но вот евклидово расстояние до среднего значения у обоих точек одинаково. Соответственно, простое евклидово расстояние до среднего значения нам не подойдет.
Как мы видим из картинки Выше, переменные между собой коррелируют, и довольно сильно. Если бы они не коррелировали между собой, или коррелировали намного меньше, мы могли бы закрыть глаза и применить евклидово расстояние для определенных задач, но здесь нам нужно сделать поправку на корреляцию и принять ее во внимание.
С этим как раз справляется расстояние Махалонобиса. Поскольку в обычно датасетах переменных больше чем двух, вместо корреляции мы будем использовать ковариационную матрицу:
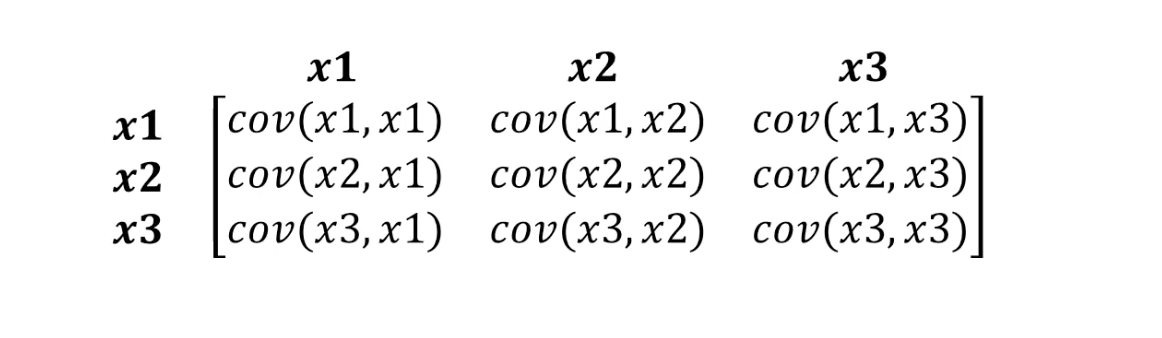
Что на самом деле делает расстояние Махалонобиса:
Посмотрим на формулу, как вычисляется расстояние Махалонобиса:

Давайте разберемся, что означают составляющие нашей формулы:
Из формулы можно понять очень важную вещь. Мы по факту умножаем на перевернутую ковариационную матрицу. В этом случае, чем выше корреляция между переменными, тем скорее всего мы сократим дистанцию, так как будем домножать на обратное большему — то есть меньшее число (если простыми словами).
Не будем пожалуй вдаваться в детали линейной алгебры, все что нам следует понять — мы измеряем расстояние между точками таким образом, чтобы принять во внимание дисперсию наших переменных и ковариацию между ними.
Фильтр Калмана
Чтобы понять, что это крутая, проверенная штука, которая может применяться в очень многих областях, достаточно знать, что фильтр Калмана применялся в 1960-х. Да-да, я намекаю именно на это — полет на Луну. Он применялся там в нескольких местах, включая работу с траекторий полета туда и обратно. Фильтр Калмана также часто применяется в анализе временных рядов на финансовых рынках, в анализе показателей различных датчиков на заводах, предприятиях и много где еще. Надеюсь, мне удалось вас немного заинтриговать и мы вкратце опишем фильтр Калмана и как он работает. Я также советую прочитать вот эту статью на Хабре, если Вы хотите узнать о нем подробнее.
Итак, мы теперь знаем, что такое фильтр Калмана и расстояние Махалонобиса. Технология DeepSORT просто связывает эти два понятия между собой для того, чтобы переносить информацию от одного кадра к другому, и добавляет новую метрику, под названием appearance. Сначала с помощью object detection определяются позиция, размер и класс одного bounding box. Потом можно в принципе применить Венгерский алгоритм, чтобы связать определенные объекты с ID объектов, которые раньше были на кадре и отслеживаются с помощью фильтров Калмана — и все будет супер, как в оригинальном SORT. Но технология DeepSORT позволяет улучшить точность определения и уменьшить количество переключений между объектами, когда, допустим, один человек на кадре загораживает ненадолго другого, и теперь человек, которого загородили, считается новым объектом. Как она это делает?
Она добавляет крутой элемент в свою работу — так называемый «внешний вид» людей, которые появляются на кадре (appearance). Этот внешний вид был натренирован отдельной нейронной сетью, которая была создана авторами DeepSORT. Они использовали порядка 1,100,000 картинок с более 1000 разных людей, чтобы нейронная сеть правильно предсказывала В оригинальном SORT есть проблема — так как там не используется внешний вид объекта, то по факту, когда объект что-то закрывает на несколько кадров (например, другой человек или колона внутри здания), то алгоритм затем присваивает другой ID этому человеку — в следствие чего так называемая «память» об объектах у оригинального SORT довольно краткосрочная.
Итак, теперь объекты имеют два свойства — их динамика движения и их внешний вид. Для динамики у нас есть показатели, которые фильтруются и предсказываются с помощью фильтра Калмана — (u,v,a,h,u’,v’,a’,h’), где u,v — это позиция предсказанного прямоугольника по X и Y, a — это соотношение сторон предсказанного прямоугольника (aspect ratio), h — высота прямоугольника, ну и производные по каждой величине. Для внешнего вида тренировали нейронную сеть, которая имела структуру:
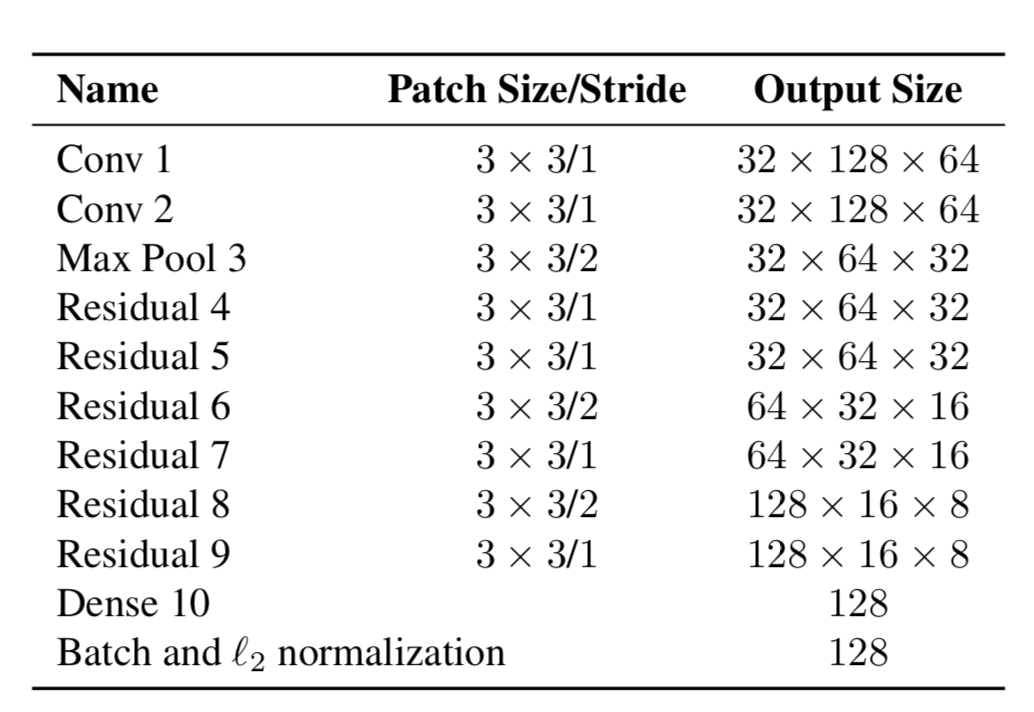
И в конце выдавала feature vector, размером 128x1. А дальше, вместо того, чтобы считать дистанцию между определенными объектами с помощью YOLO, и объектами, за которыми мы уже следили на кадре, а потом приписывать определенный ID просто с помощью расстояния Махалонобиса, авторы создали новую метрику для подсчета расстояния, которая включает в себя как предсказания с помощью фильтров Калмана, так и «косинусовое расстояние» (cosine distance), как называют его иначе, коэффициент Отиаи.
В итоге расстояние от определенного YOLO объекта до предсказанного фильтром Калмана объекта (или объекта, который уже есть в числе тех, который наблюдался на предыдущих кадрах) равно:

Где Da — это дистанция по внешней схожести, а Dk — расстояние Махалонобиса. Дальше эта гибридная дистанция применяется в Венгерском алгоритме, чтобы как раз правильно отсортировать определенные объекты с имеющимися ID.
Таким образом, простая дополнительная метрика Da помогла создать новый, элегантный алгоритм DeepSORT, который применяется во многих проблемах и является довольно популярным в задаче Object Tracking.
Статья получилась довольно увесистой, спасибо тем, кто дочитал до конца! Надеюсь, мне удалось рассказать что-то новое и помочь Вам в понимании того, как работает Object Tracking на YOLO и DeepSORT.
Но как именно работает Object Tracking? Есть множество Deep Learning решений для этой задачи, и сегодня я хочу рассказать о распространенном решении и о математике, которая стоит за ним.
Итак, в этой статье я попробую простыми словами и формулами рассказать про:
- YOLO — отличный object detector
- Фильтры Калмана
- Расстояние Махаланобиса
- Deep SORT
YOLO — отличный object detector
Сразу нужно сделать очень важную пометку, которую нужно запомнить — Object Detection это не Object Tracking. Для многих это не будет новостью, но часто люди путают эти понятия. Простыми словами:
Object Detection — это просто определение объектов на картинке/кадре. То есть алгоритм или нейронная сеть определяют объект и записывают его позицию и bounding boxes (параметры прямоугольников вокруг объектов). Пока что речи о других кадрах не идет, и алгоритм работает только с одним.
Пример:

Object Tracking — здесь совсем другое дело. Здесь задача не просто определить объекты на кадре, но еще и связать информацию с предыдущих кадров таким образом, чтобы не терять объект, или сделать его уникальным.
Пример:

То есть Object Tracker включает в себя Object Detection для определения объектов, и другие алгоритмы для понимания какой объект на новом кадре принадлежит какому из предыдущего кадра.
Поэтому Object Detection играет очень важную роль в задаче трэкинга.
Почему YOLO? Да потому что YOLO считается эффективнее многих других алгоритмов для определения объектов. Вот небольшой график для сравнения от создателей YOLO:

Здесь мы рассматриваем YOLOv3-4, поскольку это самые последние версии и они эффективнее предыдущих.
Архитектуры разных Object Detectors
Итак, существует несколько архитектур нейронных сетей, созданных для определения объектов. Они в основном разделяются на «двухуровневые», такие как RCNN, fast RCNN и faster RCNN, и «одноуровневые», такие как YOLO.
«Двухуровневые» нейронные сети, перечисленные выше, используют так называемые регионы на картинке, чтобы определить, находится ли в этом регионе определенный объект.
Обычно это выглядит так (для faster RCNN, которая является самой быстрой из перечисленных двухуровневых систем):
- Подается картинка/кадр на вход
- Кадр прогоняется через CNN для формирования feature maps
- Отдельной нейронной сетью определяются регионы с высокой вероятностью нахождения в них объектов
- Дальше эти регионы с помощью RoI pooling сжимаются и подаются в нейронную сеть, определяющую класс объекта в регионах

Но в этих нейронных сетях есть две ключевые проблемы: они не смотрят на картинку «полностью», а только на отдельные регионы, и они относительно медленные.
В чем же крутость YOLO? В том, что эта архитектура не имеет двух проблем свыше, и она доказала неоднократно свою эффективность.
Вообще архитектура YOLO в первых блоках не сильно отличается по «логике блоков» от других детекторов, то есть на вход подается картинка, дальше создаются feature maps с помощью CNN (правда в YOLO используется своя CNN под названием Darknet-53), затем эти feature maps определенным образом анализируются (об этом чуть позже), выдавая на выходе позиции и размеры bounding boxes и классы, которым они принадлежат.

Но что такое Neck, Dense Prediction и Sparse Prediction?
С Sparse Prediction мы разобрались немного ранее — это просто повторение того, как двухуровневые алгоритмы работают: определяют по отдельности регионы и затем классифицируют эти регионы.
Neck (или «шея») — это отдельный блок, который создан для того, чтобы агрегировать информацию от отдельных слоев с предыдущих блоков (как показано на рисунке выше) для увеличения аккуратности предсказания. Если Вас заинтересовало это — можете погуглить термины «Path Aggregation Network», «Spatial Attention Module» и «Spatial Pyramid Pooling».
И, наконец, то, что отличает YOLO от всех других архитектур — блок под названием (на нашей картинке выше) Dense Prediction. На нем мы сфокусируемся чуть сильнее, потому что это очень интересное решение, которое как раз позволило YOLO вырваться в лидеры по эффективности определения объектов.
YOLO (You Only Look Once) несет в себе философию смотреть на картинку один раз, и за этот один просмотр (то есть один прогон картинки через одну нейронную сеть) делать все необходимые определения объектов. Как это происходит?
Итак, на выходе от работы YOLO мы обычно хотим вот это:

Что делает YOLO когда учится на данных (простыми словами):
Шаг 1: Обычно картинки решейпят под размер 416x416 перед началом обучения нейронной сети, чтобы можно было их подавать батчами (для ускорения обучения).
Шаг 2: Делим картинку (пока что мысленно) на клетки размером axa. В YOLOv3-4 принято делить на клетки размером 13x13 (о различных скейлах поговорим чуть позже, чтобы было понятнее).

Теперь фокусируемся на эти клеточках, на которые мы разделили картинку/кадр. Такие клетки, которые называются grid cells, лежат в основе идеи YOLO. Каждая клетка является «якорем», к которому прикрепляются bounding boxes. То есть вокруг клетки рисуются несколько прямоугольников для определения объекта (поскольку непонятно, какой формы прямоугольник будет наиболее подходящим, их рисуют сразу несколько и разных форм), и их позиции, ширина и высота вычисляются относительно центра этой клетки.

Как же рисуются эти прямоугольники (bounding boxes) вокруг клетки? Как определяется их размер и позиция? Здесь в борьбу вступает техника anchor boxes (в переводе — якорные коробки, или «якорные прямоугольники»). Они задаются в самом начале либо самим пользователем, либо их размеры определяются исходя из размеров bounding boxes, которые есть в датасете, на котором будет тренироваться YOLO (используется K-means clustering и IoU для определения самых подходящих размеров). Обычно задают порядка 3 различных anchor boxes, которые будут нарисованы вокруг (или внутри) одной клетки:

Зачем это сделано? Сейчас все будет понятно, так как мы обсудим то, как YOLO обучается.
Шаг 3. Картинка из датасета прогоняется через нашу нейронную сеть (заметим, что кроме картинки в тренировочном датасете у нас должны быть определенны позиции и размеры настоящих bounding boxes для объектов, которые есть на ней. Это называется «аннотация» и делается это в основном вручную).
Давайте теперь подумаем, что нам нужно получить на выходе.
Для каждой клетки, нам нужно понять две принципиальные вещи:
- Какой из anchor boxes, из 3 нарисованных вокруг клетки, нам подходит больше всего и как его можно немного подправить для того, чтобы он хорошо вписывал в себя объект
- Какой объект находится внутри этого anchor box и есть ли он вообще
Какой же должен быть тогда output у YOLO?
1. На выходе для каждой клетки мы хотим получить:

2. Output должен включать в себя вот такие параметры:

Как определяется objectness? На самом деле этот параметр определяется с помощью метрики IoU во время обучения. Метрика IoU работает так:

В начале Вы можете выставить порог для этой метрики, и если Ваш предсказанный bounding box будет выше этого порога, то у него будет objectness равной единице, а все остальные bounding boxes, у которых objectness ниже, будут исключены. Эта величина objectness понадобится нам, когда мы будем считать общий confidence score (на сколько мы уверены, что это именно нужный нам объект расположен внутри предсказанного прямоугольника) у каждого определенного объекта.
А теперь начинается самое интересное. Представим, что мы создатели YOLO и нам нужно натренировать ее на то, чтобы распознавать людей на кадре/картинке. Мы подаем картинку из датасета в YOLO, там происходит feature extraction в начале, а в конце у нас получается CNN слой, который рассказывает нам о всех клеточках, на которые мы «разделили» нашу картинку. И если этот слой рассказывает нам «неправду» о клеточках на картинке, то у нас должен быть большой Loss, чтобы потом его уменьшать при подаче в нейронную сеть следующих картинок.
Чтобы было совсем понятно, есть очень простая схема с тем, как YOLO создает этот последний слой:

Как мы видим из картинки, этот слой, размером 13x13 (для картинок изначального размера 416x416) для того, чтобы рассказывать про «каждую клетку» на картинке. Из этого последнего слоя и достается информация, которую мы хотим.
YOLO предсказывает 5 параметров (для каждого anchor box для определенной клетки):

Чтобы было легче понять, есть хорошая визуализация на эту тему:

Как можно понять их этой картинки, задача YOLO — максимально точно предсказать эти параметры, чтобы максимально точно определять объект на картинке. А confidence score, который определяется для каждого предсказанного bounding box, является неким фильтром для того, чтобы отсеять совсем неточные предсказания. Для каждого предсказанного bounding box мы умножаем его IoU на вероятность того, что это определенный объект (вероятностное распределение рассчитывается во время обучения нейронной сети), берем лучшую вероятность из всех возможных, и если число после умножения превышает определенный порог, то мы можем оставить этот предсказанный bounding box на картинке.
Дальше, когда у нас остались только предсказанные bounding boxes с высоким confidence score, наши предсказания (если их визуализировать) могут выглядеть примерно вот так:

Мы можем теперь использовать технику NMS (non-max suppression), чтобы отфильтровать bounding boxes таким образом, чтобы для одного объекта был только один предсказанный bounding box.

Нужно также знать, что YOLOv3-4 предсказывают на 3-х разных скейлах. То есть картинка делится на 64 grid cells, на 256 клеток и на 1024 клетки, чтобы также видеть маленькие объекты. Для каждой группы клеток алгоритм повторяет необходимые действия во время предсказания/обучения, которые были описаны сверху.
В YOLOv4 было использовано много техник для увеличения точности модели без сильной потери скорости. Но для самого предсказания оставили Dense Prediction таким же, как и у YOLOv3. Если Вы интересуетесь тем, что же такого магического сделали авторы, чтобы поднять так точность не теряя скорости, есть отличная статья, написанная про YOLOv4.
Надеюсь мне удалось немного донести то, как работает YOLO в целом (точнее последние две версии, то есть YOLOv3 и YOLOv4), и в Вас это пробудит желание воспользоваться этой моделью в будущем, или узнать про ее работу чуть подробнее.
Раз мы разобрались с, пожалуй, лучшей нейронной сетью для Object Detection (если оценивать скорость/качество), давайте наконец перейдем к тому, как же нам связывать информацию о наших определенных YOLO объектов между кадрами видео. Как программа может понимать, что человек на предыдущем кадре — это тот же человек, что и на новом?
Deep SORT
Для понимания этой технологии, следует сначала разобраться с парой математических аспектов — расстояние Махалонобиса и фильтр Калмана.
Расстояние Махалонобиса
Рассмотрим очень простой пример, чтобы интуитивно понять, что такое расстояние Махолонобиса и зачем оно нужно. Многим, наверное, известно, что такое евклидово расстояние. Обычно, это расстояние от одной точки до другой в евклидовом пространстве:
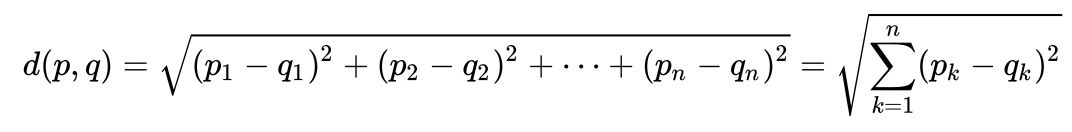

Допустим, у нас есть две переменные — X1 и X2. Для каждой из них у нас есть много измерений.

Теперь, допустим, у нас появилось 2 новых измерения:

Как понять, какое из этих двух значений наиболее подходит для нашего распределения? На глаз все очевидно — точка 2 нам подходит. Но вот евклидово расстояние до среднего значения у обоих точек одинаково. Соответственно, простое евклидово расстояние до среднего значения нам не подойдет.
Как мы видим из картинки Выше, переменные между собой коррелируют, и довольно сильно. Если бы они не коррелировали между собой, или коррелировали намного меньше, мы могли бы закрыть глаза и применить евклидово расстояние для определенных задач, но здесь нам нужно сделать поправку на корреляцию и принять ее во внимание.
С этим как раз справляется расстояние Махалонобиса. Поскольку в обычно датасетах переменных больше чем двух, вместо корреляции мы будем использовать ковариационную матрицу:
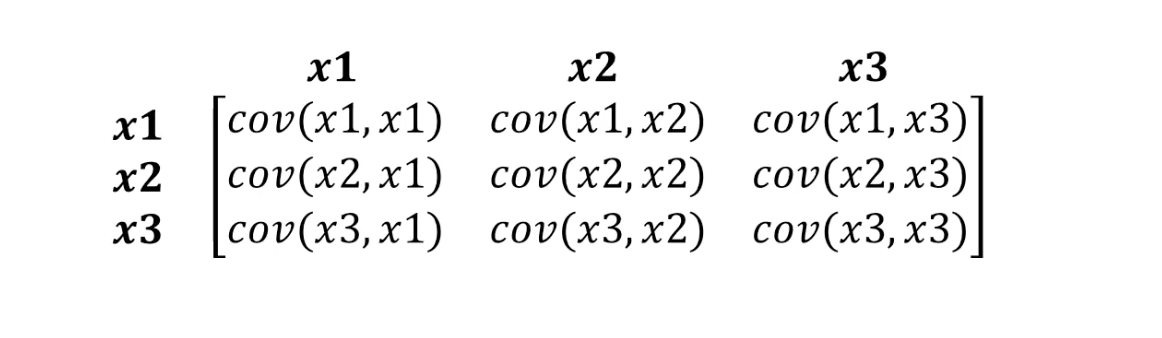
Что на самом деле делает расстояние Махалонобиса:
- Избавляется от ковариации переменных
- Делает дисперсию (variance) переменных равной 1
- После этого использует обычное евклидово расстояние для трансформированных данных
Посмотрим на формулу, как вычисляется расстояние Махалонобиса:

Давайте разберемся, что означают составляющие нашей формулы:
- Эта разница — разница между нашей новой точкой и средними значениями для каждой переменной
- S — это ковариационная матрица, о которой мы говорили чуть ранее
Из формулы можно понять очень важную вещь. Мы по факту умножаем на перевернутую ковариационную матрицу. В этом случае, чем выше корреляция между переменными, тем скорее всего мы сократим дистанцию, так как будем домножать на обратное большему — то есть меньшее число (если простыми словами).
Не будем пожалуй вдаваться в детали линейной алгебры, все что нам следует понять — мы измеряем расстояние между точками таким образом, чтобы принять во внимание дисперсию наших переменных и ковариацию между ними.
Фильтр Калмана
Чтобы понять, что это крутая, проверенная штука, которая может применяться в очень многих областях, достаточно знать, что фильтр Калмана применялся в 1960-х. Да-да, я намекаю именно на это — полет на Луну. Он применялся там в нескольких местах, включая работу с траекторий полета туда и обратно. Фильтр Калмана также часто применяется в анализе временных рядов на финансовых рынках, в анализе показателей различных датчиков на заводах, предприятиях и много где еще. Надеюсь, мне удалось вас немного заинтриговать и мы вкратце опишем фильтр Калмана и как он работает. Я также советую прочитать вот эту статью на Хабре, если Вы хотите узнать о нем подробнее.
Фильтр Калмана
Мы разберем сейчас одномерный пример, чтобы просто понять как работает фильтр Калмана для одной переменной. Для нескольких переменных алгоритм никак не отличается, правда там будут задействованы матрицы, о которых я кратко упомяну в процессе.
Допустим у нас есть термометр и чашка с водой, температуру которой мы хотим измерить. У термометра есть своя погрешность в 4 градуса по Цельсию. Допустим, настоящая температура воды в чашке порядка 72 градусов.
Фильтр Калмана считает 3 принципиально важные вещи:
1) Усиление Калмана (Kalman Gain):

Сразу прошу прощения за картинки, у Хабра какие-то проблемы с формулами (или я не до конца разобрался почему они у меня не отображаются).
2) Оцениваем значение нужной нам переменной на ЭТОМ этапе, с учетом посчитанного нами усиления Калмана и показаний с датчиков (в нашем случае, показание термометра), а также значений с предыдущего этапа, который происходил в прошлом.

3) Оцениваем НОВУЮ ошибку (неопределенность), чтобы применить ее на следующем этапе:
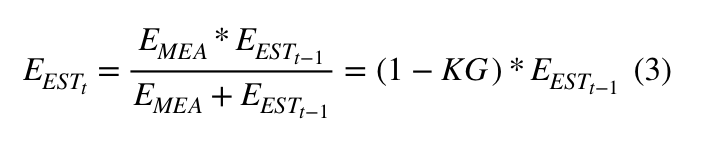
Таким образом, весь алгоритм может выглядеть вот так:
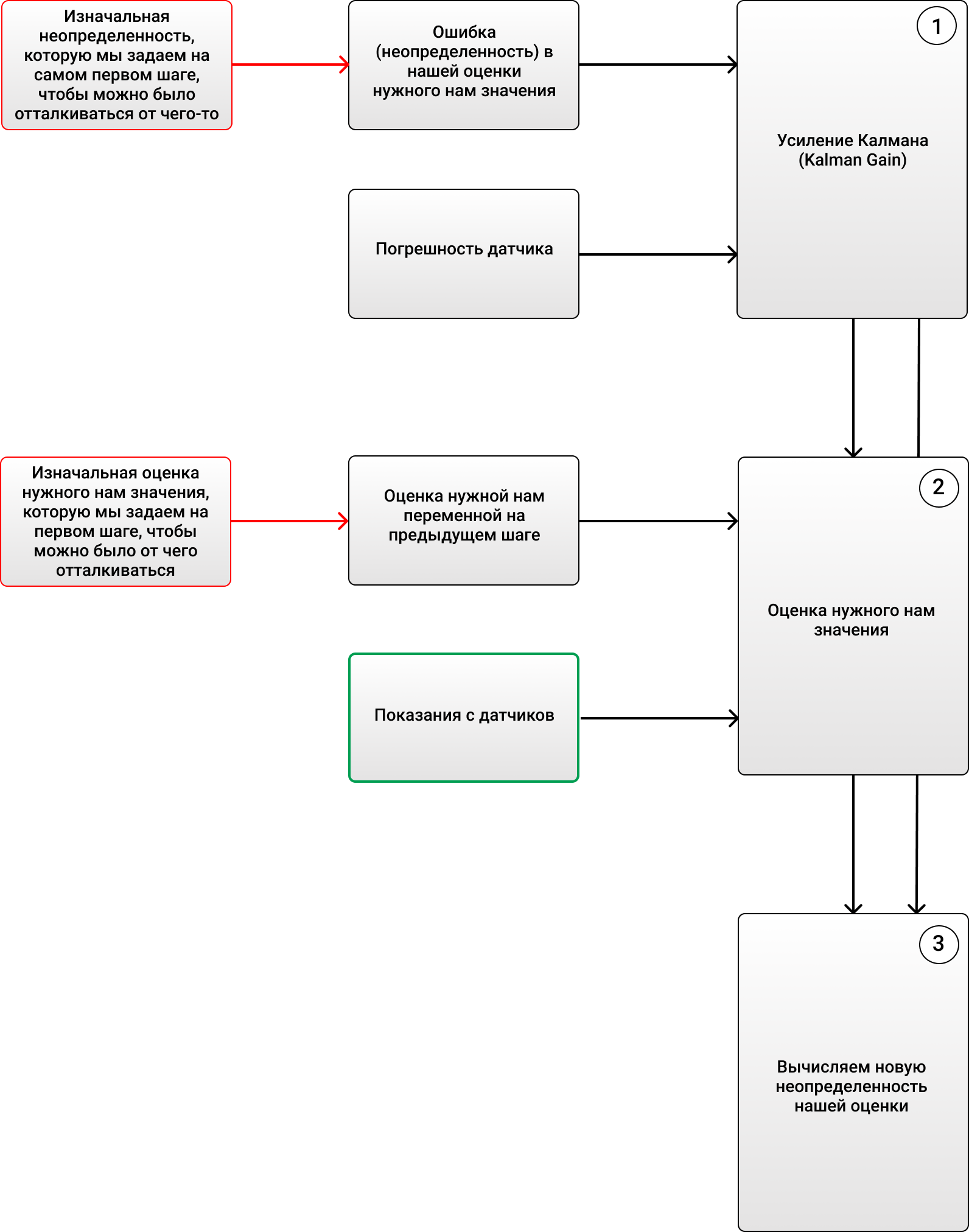
Итак, допустим мы задали изначальную температуру 69 градусов (прикинули примерно), с ошибкой в 2 градуса. Тогда, зная, что у термометра погрешность примерно 4 градуса (ага, супер точный термометр, ну это в моей Вселенной), наше значение KG по формуле (1) будет равно 2/(2+4) = 0.33. Дальше мы можем легко измерить наше новое значение воды (более точное), вставив термометр в воду и померив температуру. Получилось 70 градусов (допустим), и теперь мы можем более точно оценить температуру воды в стакане. Она будет равна по формуле (2), где нам теперь известно все, 68+0.33(70-68)=68.66. А наша новая ошибка по формуле (3) будет равна (1-0.33)2 = 1.32. Теперь на следующих шагах мы будем применять соответсвенно вычисленные нами новые значения для ошибки, температуры воды, и будем смотреть на новые показания прибора, когда мы его заново опустим в воду. График будет выглядеть примерно вот так:
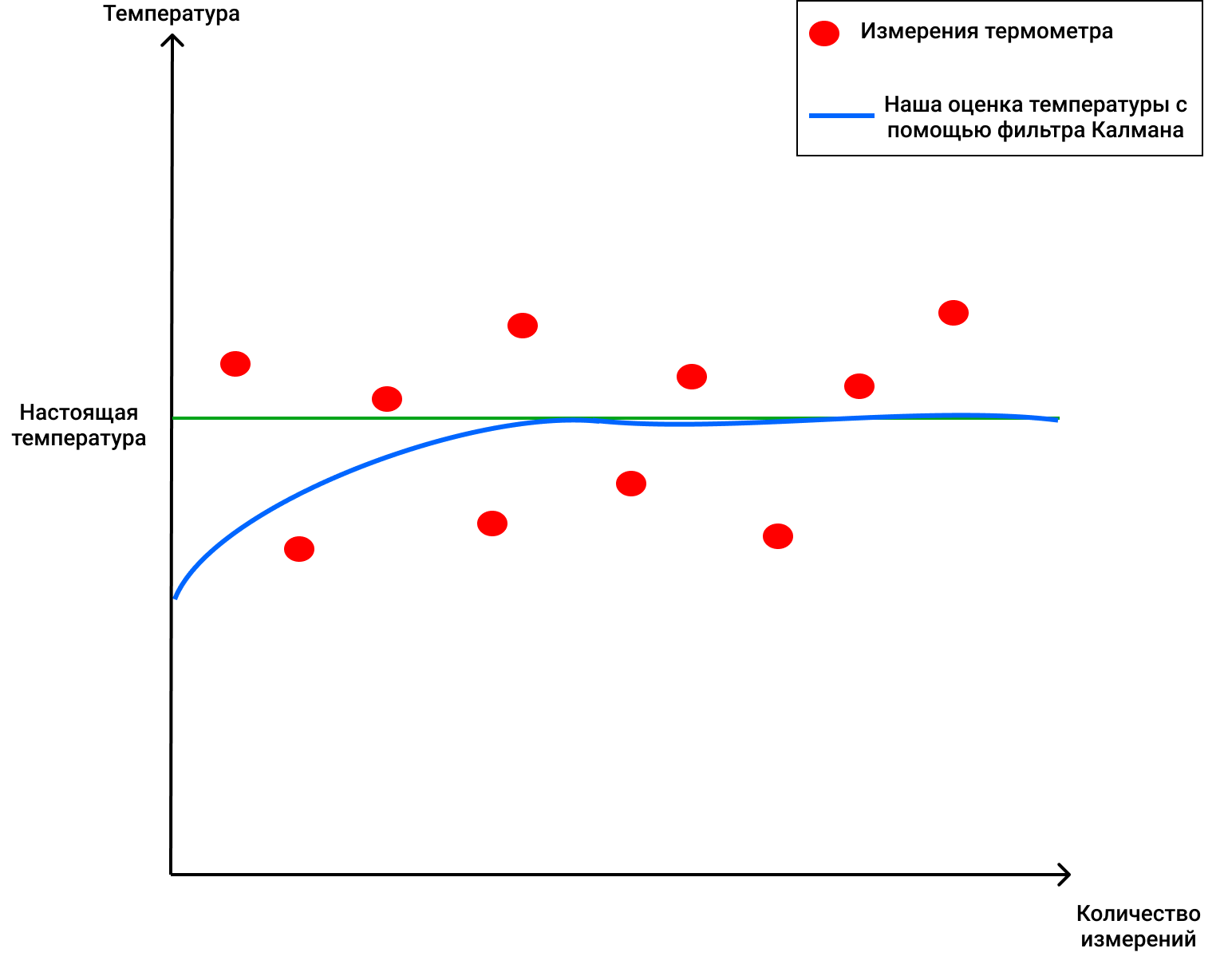
Это потрясающе, как фильтр Калмана может избавлять нас от шума и помогать находить настоящее значение!
Если же у нас есть несколько величин, которые мы хотим использовать для предсказания, то мы будем использовать матрицы, а алгоритм не поменяется, правда немного изменится то, как мы считаем определенные величины (об этом вы можете прочитать в разных постах на Хабре о фильтре Калмана, одну из них я прикреплял выше).
Допустим у нас есть термометр и чашка с водой, температуру которой мы хотим измерить. У термометра есть своя погрешность в 4 градуса по Цельсию. Допустим, настоящая температура воды в чашке порядка 72 градусов.
Фильтр Калмана считает 3 принципиально важные вещи:
1) Усиление Калмана (Kalman Gain):

Сразу прошу прощения за картинки, у Хабра какие-то проблемы с формулами (или я не до конца разобрался почему они у меня не отображаются).
2) Оцениваем значение нужной нам переменной на ЭТОМ этапе, с учетом посчитанного нами усиления Калмана и показаний с датчиков (в нашем случае, показание термометра), а также значений с предыдущего этапа, который происходил в прошлом.

3) Оцениваем НОВУЮ ошибку (неопределенность), чтобы применить ее на следующем этапе:
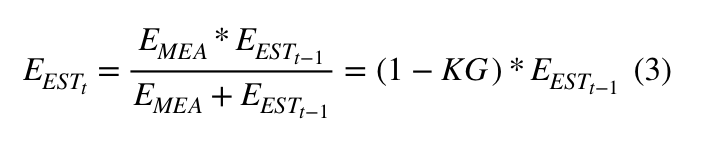
Таким образом, весь алгоритм может выглядеть вот так:

Итак, допустим мы задали изначальную температуру 69 градусов (прикинули примерно), с ошибкой в 2 градуса. Тогда, зная, что у термометра погрешность примерно 4 градуса (ага, супер точный термометр, ну это в моей Вселенной), наше значение KG по формуле (1) будет равно 2/(2+4) = 0.33. Дальше мы можем легко измерить наше новое значение воды (более точное), вставив термометр в воду и померив температуру. Получилось 70 градусов (допустим), и теперь мы можем более точно оценить температуру воды в стакане. Она будет равна по формуле (2), где нам теперь известно все, 68+0.33(70-68)=68.66. А наша новая ошибка по формуле (3) будет равна (1-0.33)2 = 1.32. Теперь на следующих шагах мы будем применять соответсвенно вычисленные нами новые значения для ошибки, температуры воды, и будем смотреть на новые показания прибора, когда мы его заново опустим в воду. График будет выглядеть примерно вот так:

Это потрясающе, как фильтр Калмана может избавлять нас от шума и помогать находить настоящее значение!
Если же у нас есть несколько величин, которые мы хотим использовать для предсказания, то мы будем использовать матрицы, а алгоритм не поменяется, правда немного изменится то, как мы считаем определенные величины (об этом вы можете прочитать в разных постах на Хабре о фильтре Калмана, одну из них я прикреплял выше).
DeepSORT — наконец-то!
Итак, мы теперь знаем, что такое фильтр Калмана и расстояние Махалонобиса. Технология DeepSORT просто связывает эти два понятия между собой для того, чтобы переносить информацию от одного кадра к другому, и добавляет новую метрику, под названием appearance. Сначала с помощью object detection определяются позиция, размер и класс одного bounding box. Потом можно в принципе применить Венгерский алгоритм, чтобы связать определенные объекты с ID объектов, которые раньше были на кадре и отслеживаются с помощью фильтров Калмана — и все будет супер, как в оригинальном SORT. Но технология DeepSORT позволяет улучшить точность определения и уменьшить количество переключений между объектами, когда, допустим, один человек на кадре загораживает ненадолго другого, и теперь человек, которого загородили, считается новым объектом. Как она это делает?
Она добавляет крутой элемент в свою работу — так называемый «внешний вид» людей, которые появляются на кадре (appearance). Этот внешний вид был натренирован отдельной нейронной сетью, которая была создана авторами DeepSORT. Они использовали порядка 1,100,000 картинок с более 1000 разных людей, чтобы нейронная сеть правильно предсказывала В оригинальном SORT есть проблема — так как там не используется внешний вид объекта, то по факту, когда объект что-то закрывает на несколько кадров (например, другой человек или колона внутри здания), то алгоритм затем присваивает другой ID этому человеку — в следствие чего так называемая «память» об объектах у оригинального SORT довольно краткосрочная.
Итак, теперь объекты имеют два свойства — их динамика движения и их внешний вид. Для динамики у нас есть показатели, которые фильтруются и предсказываются с помощью фильтра Калмана — (u,v,a,h,u’,v’,a’,h’), где u,v — это позиция предсказанного прямоугольника по X и Y, a — это соотношение сторон предсказанного прямоугольника (aspect ratio), h — высота прямоугольника, ну и производные по каждой величине. Для внешнего вида тренировали нейронную сеть, которая имела структуру:

И в конце выдавала feature vector, размером 128x1. А дальше, вместо того, чтобы считать дистанцию между определенными объектами с помощью YOLO, и объектами, за которыми мы уже следили на кадре, а потом приписывать определенный ID просто с помощью расстояния Махалонобиса, авторы создали новую метрику для подсчета расстояния, которая включает в себя как предсказания с помощью фильтров Калмана, так и «косинусовое расстояние» (cosine distance), как называют его иначе, коэффициент Отиаи.
В итоге расстояние от определенного YOLO объекта до предсказанного фильтром Калмана объекта (или объекта, который уже есть в числе тех, который наблюдался на предыдущих кадрах) равно:

Где Da — это дистанция по внешней схожести, а Dk — расстояние Махалонобиса. Дальше эта гибридная дистанция применяется в Венгерском алгоритме, чтобы как раз правильно отсортировать определенные объекты с имеющимися ID.
Таким образом, простая дополнительная метрика Da помогла создать новый, элегантный алгоритм DeepSORT, который применяется во многих проблемах и является довольно популярным в задаче Object Tracking.
Статья получилась довольно увесистой, спасибо тем, кто дочитал до конца! Надеюсь, мне удалось рассказать что-то новое и помочь Вам в понимании того, как работает Object Tracking на YOLO и DeepSORT.


ZlodeiBaal
Норм статья. Только пара моментов:
В целом я всё это месяц назад в статье своей на хабре рассказывал.
AbellAI Автор
Спасибо большое за комментарий, все по делу)
Ajex
Я использовал эту библиотеку github.com/abewley/sort
работала у меня и на PyTorch (Detectron2) и на TensorFlow (Mask_RCNN) для определения движущихся объектов на потоке с камеры.
Но спасибо за объяснение того, как оно реально работает. Полезно.