Формальная теория моделирования использует алгебраические отношения, включая их в сигнатуры моделей алгебраических структур, которыми описывает реальные физические, технические и информационные объекты, процессы их функционирования. К числу последних я отношу, например, базы данных (реляционные базы данных (РеБД)). Не менее важной считаю область принятия решений, которая состоит из двух основных статистической и алгебраической, основанной целиком на теории отношений. Образовательный уровень специалистов в этой теории близок к нулю.

Откройте учебник по специализации и там увидите в лучшем случае об эквивалентностях, которые авторами трактуются весьма своеобразно. Одного защитившегося уже ДТН спрашиваю: Вы рассматриваете отношение эквивалентности на указывая ни носителя отношения, ни конкретного отношения, как оно у Вас выглядит в записи? Ответ: как выглядит — обыкновенно. Выясняется, что он обо всем этом имеет весьма смутное представление.

Публикаций по проектированию РеБД, кроме иностранных статей назвать затрудняюсь. В 90-х годах был оппонентом, писал отзыв на диссертацию, где рассматривались и иерархические, и сетевые, и реляционные БД. Но как-то год, полтора назад опять на отзыв пришла работа, автор пишет уже только о РеБД, о нормализации отношений БД, но теоретической новизны не показал. Во многих ВУЗах читается курс о базах данных, но не о том, как их создать, создать СУБД, а как правило, о том как эксплуатировать готовую (зарубежную) БД.

Преп. состав не готов научить специалистов IТ-шников создавать отечественные СУБД, ОS, языки программирования, я уж не говорю о БИС, СБИС, заказных БИС. Здесь, по-видимому, поезд ушел давно и надолго. Так что напрасно надуваются у некоторых щеки от гордости (читай снобизма) это видно по комментариям к чужим публикациям, покажите сами, что можете, а не балуйтесь никчемными переводами и перепевками чужого ради предмета гордости — «рейтинга» и «кармы». Сказывается не только отсутствие креатива, но простой образованности и воспитания.

Вторая предметная область неразрывно, связанная с отношениями, — принятие решений. Каждый из нас постоянно занят этим. Мы без решения осознанного или неосознанного пальцем не пошевелим. Мало кто понимает, а еще меньше пишет о решениях. В основе решения любого ЛПР (лица, принимающего решение) лежит предпочтение альтернатив. А моделью предпочтения как раз и является такой тип отношений, который назван «пространством отношений предпочтения». Но кто их изучает. Когда я пришел к «специалисту» по отношениям с вопросом о количестве отношений каждого типа, он не зная ответа, «убил» встречным вопросом, а зачем это Вам?

Понятие отношения

Думаю, что термин отношение знаком каждому читателю, но просьба дать определение поставит большинство в тупик. Причин для этого много. Они чаще всего в преподавателях, которые, если и использовали отношения в процессе преподавания, внимания на этом термине не заостряли, запоминающихся примеров, по-видимому, не приводили.

В моей памяти есть несколько на всю жизнь запомнившихся примеров. Об отображениях и об отношениях. Расскажу вначале об отображениях. Имеется два ведерка с краской. В одном белая в другом — черная. И есть коробка с кубиками (очень много). Грани имеют рельефные номера. Сколькими способами можно раскрасить грани кубиков в два цвета? Ответ неожиданный — столькими, сколько 6-разрядных двоичных чисел, или 2⁶ = 64. Поясню подробнее ф: 2>6 отображаются 2 объекта в 6. Каждая строчка таблицы- дискретное отображение фi.

Построим таблицу с 6 колонками и краскам сопоставим число белая — нуль, черная — единица, а граням кубика колонки. Начинаем с того, что все 6 граней белые — это 6-мерный нулевой вектор. Вторая строчка одна грань черная, т. е. младший разряд заполнен 1. и так до исчерпания 6-разрядных двоичных чисел. Кубики ставим в общий длинный ряд. У каждого из них как бы появился номер от 0 до 63.

Теперь отображение наоборот. Пачка листов бумаги (много) и 6 красок (фломастеры).
Фломастерами разного цвета надо пометить обе стороны бумажных листов. Сколько листов потребуется. Ответ f: 6 > 2 или 6² =36. Речь идет о произвольных отображениях.

Перейдем к отношениям. Начнем с абстрактного множества — носителя отношения
А ={a1, a2, a3, ..., an}.
О нем почитать можно здесь. Для лучшего понимания сократим множество до 3 элементов, т.е. А ={a1, a2, a3}. Теперь выполним декартово умножение А?А =А²,
А?А={(a1, a1),(a1, а2),(a1, a3),(a2, а1),(a2, a2),(a2, a3),(a3, a1),(a3, a2),(a3, a3)}.

Получили 9 упорядоченных пар элементов из А?А, в паре первый элемент из первого сомножителя, второй — из второго. Теперь попробуем получить все подмножества из декартова квадрата А?А. Вначале простенький пример.

Пример 1. Задано множество А ={a,b,c,d} из 4-х элементов. Выписать все его подмножества. В(А) ={O};{a};{b};{c};{d};{ab};{ac};{ad};{bc};{bd};{cd};{abc};{abd};{acd};{bcd};{abcd}; 2⁴ = 16 подмножеств. Это булеан В(А) множества А и в него включено пустое подмножество.

Подмножества будут содержать из А?А разное количество элементов (пар): одну, две, три и так до всех 9 пар, включаем в этот список и пустое множество (O). Сколько же получилось подмножеств? Много, а именно 2⁹= 512 элементов.

Определение. Любое подмножество декартова произведения (у нас квадрата) множества называется отношением. Заметим, в произведении используется одно и то же множество. Если множества разные, возникает не отношение, а соответствие.

Если декартово произведение из двух сомножителей, то отношение бинарное, если из 3-х -тернарное, из 4-х — тетрарное, из n — n-арное. Арность — число мест в отношении. Отношениям дают имена прописных букв R,H, P, S… Остановимся подробно на бинарных отношениях (БО), так как они играют очень важную роль в теории отношений. Собственно к бинарным отношениям могут быть сведены все остальные.

Символ отношения ставится слева от элементов R(x, y) или между ними x R y; х, у є А.
Определение Множество всех подмножеств множества А называется булеаном. Наш булеан состоит из 2^|А?А| элементов, здесь|А?А| — мощность множества.

Отношения можно задавать в разном представлении над А={a1,a2,a3,a4}:

• перечислением элементов; R1={(a1,a2),(a1,a3),(a2,a3)(a2,a4)(a3,a2)(a3,a4}
• двоичным n = 16-разрядным вектором; <0110001101010000>;
• матрицей;

Рисунок 1.2. а)Матрица 4?4 бинарного отношения б) нумерация клеток Матрицы

Здесь используются номера клеток, заполненные единицами на рис. 1б)
— Векторное представление. Двоичный вектор для представления бинарного отношения формируется из элементов {0,1} следующим образом:

Рассмотренный пример задания отношения в векторной форме будет иметь следующий вид:


— Представление графом. Поставим в соответствие элементам множества
А ={x1,x2,z3,...,xn} точки на плоскости, т.е. вершины графа G = [Q, R].

Проведем в графе дугу от (xi) к (xj) тогда и только тогда, когда пара (xi,xj) є R (при i = j дуга (xi,xi) превращается в петлю при вершине (xi). Пример (рис. 1а) представления бинарного отношения A[4?4] графом изображен на рис.2.2.

Рисунок 2.2. Представление отношения ориентированным графом

Каталог бинарных отношений (n = 3)

Большое видится на расстоянии. Чтобы почувствовать отношения их разнообразие, мощность мне пришлось вручную создать каталог бинарных отношений над множеством из 3-х элементов, который включил все (боле 500 отношений) отношения. После этого «дошло» или «зашло»об отношениях.

Очевидно, что в каталог войдут 2^3?3 = 2⁹ отношений, и каждое из них снабдим набором присущих им свойств. Ниже (табл. 3) приводится полный список всех 512 отношений над множеством А, |A| = 3, из трех элементов. Приводятся также результаты подсчета количества отношений (табл. 2), представленных сочетаниями номеров клеток декартова квадрата 3?3, различных подклассов для различных значений мощности множества-носителя (n = 3). Для каждого отношения указаны его основные свойства и принадлежность типу (табл. 3). Сокращения, используемые в каталоге раскрываются таблицей 2
Таблица 2. Количественные характеристики каталога при разных n


Сущность производимых операций с отношениями и их технику удобно пояснять на примерах, которые особенно просты и понятны для бинарных отношений. В операциях могут участвовать, два и/или более отношений. Операции, выполняемые над отдельными отношениями – унарные операции. Например, операции обращения (получение обратного) отношения, взятие дополнения, сужение (ограничение) отношения. Как пользоваться каталогом поясним примером примером.

Пример 2. Рассмотрим строку Nпр =14 таблицы каталога. Она имеет вид

Первые 9 символов строки (справа от равенства) — это двоичный вектор, соответствующий сочетанию из 9 по 2, а именно, номер первой клетки (отсчет слева направо) номер 5-й клетки матрицы бинарного отношения, т.е. элементы а1а1= а2а2 =1. Это сочетание имеет порядковый номер Ncч = 4 и сквозной номер Nпр = 14 в списке всех отношений. В остальных позициях этой строки стоят либо нули, либо единицы. Нули свидетельствуют об отсутствии свойства, соответствующего названию колонки нуля, а единицы – наличие такого свойства у рассматриваемого отношения.

Свойства и количественные характеристики отношений

Рассмотрим наиболее важные свойства отношений, которые позволят в дальнейшем выделить типы (классы) отношений, применяющиеся в реляционных базах данных в теории выбора и принятия решений и других приложениях. Далее будем обозначать отношение символом [R,?]. R- имя отношения, ? — множество-носитель отношения.

1. Рефлексивность. Отношение [R,?] называется рефлексивным, если каждый элемент множества находится в отношении R сам с собой (рис. 2.3). Граф рефлексивного БО имеет во всех вершинах петли (дуги), а матрица отношения содержит (Е) единичную главную диагональ.


Рисунок 2.3. Рефлексивное отношение

2. Антирефлексивность. Отношение [R,?] называется антирефлексивным, если ни один элемент из множества не находится в отношении R сам с собой (рис. 2.4). Антирефлексивные отношения называют строгими.


Рисунок 2.4. Антирефлексивное отношение

3. Частичная рефлексивность. Отношение [R,?] называется частично
рефлексивным, если один или более элементов из множества не находится в отношении R сам с собой (рис. 2.5).


4. Симметричность. Отношение [R,?] называется симметричным, если вместе с упорядоченной парой (х, у) отношение содержит и упорядоченную пару (у, х) (рис. 2.6).


5. Антисимметричность. Отношение [R,?] называется антисимметричным, если, если для всякой упорядоченной пары (х, у) є R упорядоченная пара
(у, х)єR, только в случае х = у. Для таких отношений R?R^-1 ? E (рис. 2.7).


6. Асимметричность. Отношение [R,?] называется асимметричным, если оно антирефлексивно и для всякой упорядоченной пары (х, у) є R упорядоченная пара (у, х) ? R, для отношений R ? R^-1 = O (рис. 2.8).


7. Транзитивность. Отношение [R,?] называется транзитивным, если для всяких упорядоченных пар (х, у),(у, z) є R, в отношении R найдется упорядоченная пара (х, z) є R или если R?R?R (рис. 2.9).


8. Цикличность. Отношение [R,?] называется циклическим, если для его элементов {x1, x2, z3,..., xn} найдется подмножество элементов {xi,xi+1,...xr,...,xj,xi}, для которого можно выписать последовательность xiRxi+1R...RxjRxi. Такая последовательность называется циклом или контуром (рис. 2.10).


9. Ацикличность. Отношения, в которых отсутствуют контуры называются, ациклическими. Для ациклических отношений выполняется соотношение R^k?R = O для любого k > 1 (рис. 2.11).



10. Полнота (связность). Отношение [R,?] называется полным (связным), если для любых двух элементов (у, z) є ? один из них находится в отношении с другим (рис 2.12). Линейность. Линейные отношения – это минимально полные отношения.


Рисунок 2.12. Линейное отношение

Итак, нами установлено, что отношения, как математические объекты, обладают определенными свойствами, определение которых приведены ранее. В следующем пункте рассмотрим существо и проявление некоторых свойств:

1. Рефлексивность х є А (хRx).
2. Антирефлексивность х є А ¬(хRx).
3. Симметричность х, у є А (хRy>yRx).
4. Антисимметричность (xRy & yRx>x = y).
5. Транзитивность; х, у, z є А(хRy & yRz >xRz).
6. Цикличность; х, у є А; .
7. Полнота x,y є А (xRy, yRx);
8. Связность (x ? y> xRy, yRx).
9. Линейность x,y є А (xRy, yRx).

Анализ пространства отношений представляет сложную задачу теории и, надо отметить, далек от завершения. К основным результатам следует отнести выделение подмножеств отношений, образующих полные пространства отношений со всеми вытекающими из этого следствиями.

Количественные соотношения таких дискретных пространств представляют большой как
теоретический, так и практический интерес. Ниже рассматриваются некоторые аспекты количественных характеристик, связанных со свойствами отношений разных типов.

Операции над отношениями

Как и большинстве систем счисления с отношениями выполняются операции:

• унарные;
• бинарные;
• n-арные.

Ниже приведены таблицы булева ? сложения и умножения & двух переменных x1 и x2, сложение по mod 2 и суммирование двоичных чисел:


Выше было введено понятие бинарного отношения, как подмножества упорядоченных пар декартова произведения множеств, а также были рассмотрены свойства отношений. Кроме того, были упомянуты бинарные отношения и матричное представление отношений. Рассмотрим теперь понятие отношения более подробно, кроме того, рассмотрим основные операции бинарных отношений, наиболее важные из всего их множества для отношений.

Для них должны выполняться следующие условия:

• арность операндов в операции должна совпадать;
• результатом операции должно быть отношение той же арности.

Для бинарных и n-арных отношений должно быть выполнено: область прибытия первого операнда должна совпадать с областью отправления второго операнда.

Унарные операции над отношениями

Обращение отношений. Обратным к отношению R называется отношение R^-1, определяемое условием xR^-1y<=>yRx. Более корректно эту операцию следовало бы назвать псевдообращением, так как р·р^-1 ? Е = ?.

Пусть отношение Р записано в форме перечисления входящих в него упорядоченных пар. Если в каждой паре поменять местами компоненты, то новые пары образуют отношение P^-1, которое называют обратным к Р.

Обратное отношение к отношению P – такое отношение, которое образовано парами (ai aj), для которых (aj ai) є P^-1. Для отношений в матричной форме обратные отношения получаются путем транспонирования матрицы Р.

9. Двойственное отношение (P^d) к отношению Р – отношение, образованное всеми теми парами, которые принадлежат универсальному отношению и не принадлежат обратному отношению (дополнение к обратному):

P^d = {(ai aj) | ((ai aj) єA?A) & (ai aj)? P^-1)} =(A?A)\ P^-1.

Двойственное и обратное отношения в совокупности содержат все пары декартова произведения A?A и не имеют общих пар, они также как и отношения Р и P образуют разбиение A?A


Заметим, что ни для какого отношения Р не выполняется Р= P^d.

Сужение (РА1). Отношение [R1, A1] называется сужением отношения [R, A] на множество ?1, если ?1? ? и R1=R??1??1. Отношение РА1 на множестве А1 ? А – отношение РА1 на множестве А1, образованное всеми теми парами, которые принадлежат отношению Р и одновременно входят в состав декартова произведения А1 ? А1. Другими словами, РА1 – пересечение отношений Р и А1?А1. Пусть А1 = {a1, a3, a4}, тогда для отношений Р и Q в матричной форме отношения сужения будут иметь вид:


Бинарные операции

Операции, требующие не менее двух отношений – n-арные (n-местные). В таких операциях могут участвовать отношения только одинаковой арности. Примеры таких операций: пересечение, объединение, разность, симметрическая разность отношений и некоторые другие. Если в операции используется более чем два отношения, то она выполняется последовательно для двух первых, а затем для итогового отношения и третьего и т.д.

Иначе говоря, эти операции определены для двух отношений. При операциях над отношениями предполагается, что области задания отношений (операндов и результата) совпадают, арности отношений совпадают, и результатом операции снова является отношение той же арности. В качестве примеров будем рассматривать операции над бинарными отношениями P и Q, заданными на дискретном множестве
А = {a1, a2, a3, a4} булевыми матрицами (нули в матрицу, как правило, не вписываются):


1. Пересечение (P ? Q) – отношение, образованное всеми теми парами элементов из А, которые входят в оба отношения, т.е. общие для P и Q,
P ? Q = {(ai aj) | ((ai aj) є P) & ((ai aj) є Q)}.

Матрица отношения P ? Q получается как булево пересечение матриц P и Q:


При отсутствии таких общих пар говорят, что пересечение отношений пусто, т.е. оно является нуль-отношением. Пересечением отношений R1 и R2 (R1?R2 ) называется отношение, определяемое пересечением соответствующих подмножеств из А?А.

2. Объединение (PUQ). Объединением отношений R1 и R2 (R1UR2 ) называется отношение, определяемое объединением соответствующих подмножеств из А?А. Отношение, образованное всеми парами, составляющими или отношение P, или отношение Q, т.е. парами, принадлежащими хотя бы одному из отношений (связка ? — или объединительная)
P U Q = {(ai aj) | ((ai aj) є P) ? ( (ai aj) є Q)}.

Если в множестве А?А нет других пар, не вошедших в отношение PUQ, а пересечение их нулевое, то говорят, что отношения P и Q при объединении образуют полное отношение А?А, а их система – разбиение этого полного отношения. Объединение матриц отношений образуется как булева сумма матриц отношений:


3.Разность (P\Q) – отношение, образованное теми парами из Р, которые не входят в отношение Q
P\Q = {(ai aj) | ((ai aj) є P)&((ai aj)?Q)}.

Разность для отношений в матричном представлении имеет вид


4. Умножение отношений. Упорядоченные пары, образующие отношения могут содержать одинаковые элементы, а могут и не содержать. Среди пар, имеющих в своем составе одинаковые элементы, выделим такие упорядоченные пары, которые назовем смежными (примыкающими) и которые имеют во второй паре 1-й элемент, а в первой паре 2-й элемент один и тот же. Определим произведение смежных пар как упорядоченную пару:
( ai ak)•( ak aj) => (ai aj).

В терминах теории графов сказанное означает, что смежные пары образуют маршрут из точки (ai) в точку (aj) транзитом через точку (ak), состоящий из 2-х смежных дуг. Произведение этих дуг – третья дуга из точки (ai) в точку (aj), реализующая переход между крайними точками маршрута в том же направлении, минуя промежуточную точку (ak). Говорят, что дуга (ai aj) замыкает эти точки напрямую.

5. Симметрическая разность (P?Q) – отношение, образованное теми парами, которые входят в объединение PUQ, но не входят в пересечение P?Q. Другая форма определения объясняет название операции: P?Q образовано теми упорядоченными парами, которые являются объединением разностей P\Q и Q\P. Таким образом, выражение для симметрической разности записывается двумя разными способами:
P? Q = (PU Q)\(P ? Q) = (P\Q)U (Q\P).

Матрица симметрической разности имеет вид:


Из последней записи следует, что операция симметрической разности допускает перестановку операндов, т. е. коммутативна.

5. Композиция или произведение (P•Q) – отношение, образованное всеми парами, для которых выполняется:
P•Q = {(ai aj)|((ai ak) є P) & ((ak aj) є Q)}.

Другими словами, каждая упорядоченная пара в результирующем отношении есть результат умножения смежных пар, из которых 1-я пара принадлежит первому сомножителю-отношению, 2-я – второму сомножителю-отношению. Операция композиции не коммутативна.

Композиция (Р?Q) на множестве М – отношение R, заданное на том же множестве М, которое содержит пару (x, y), когда существует Z є M такое, что (x, z) є P и (z, y) є Q.

При матричном представлении отношений матрица композиции отношений равна булеву произведению матриц исходных отношений:


Частный случай композиции отношений – квадрат отношения.

Можно показать, используя индукцию, что n-я степень отношения определяется рекуррентно по формуле:Pⁿ=P^n-1?Р, это означает, что пара (x,y) є Pⁿ в том случае, когда в матрице Р существует цепочка элементов: такая, что (xi, xi+1)є P, 1<i<n–1.

Операция композиции обладает свойством ассоциативности (как произведение матриц).

Композиция отношений на множестве М – результат попарной композиции отношений при любой расстановке скобок. Область задания результата композиции при этом не меняется.

Композиция для булевых матриц отношений образуется в результате булева произведения матриц этих отношений.

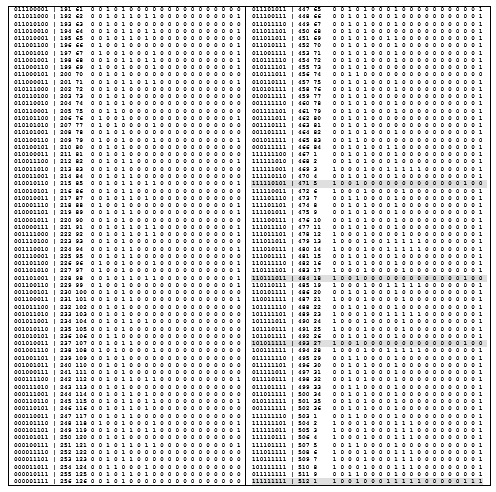
Таблица 3. Каталог бинарных отношений (n = 3). Кликабельно