Где порешать аналитические задачи от команд Яндекса? Контест и разбор / forpes.ru

21.09.2020 14:46

yaheads 0 4600 Источник

Сегодня начинается пробный раунд чемпионата по программированию Yandex Cup. Это означает, что можно с помощью системы Яндекс.Контест решать задачи, подобные тем, которые будут в квалификационном раунде. Пока результат ни на что влияет.

В посте вы найдёте условия задач трека аналитики и разборы, которые сознательно спрятаны в спойлеры. Вы можете подглядеть решение либо сначала попробовать сделать задачи самостоятельно. Проверка происходит автоматически — Контест сразу сообщит результат, и у вас будет возможность предложить другое решение.

A. Посчитать лгунов в стране

^{Решить в Контесте}

В государстве живёт 10 000 человек. Они делятся на правдолюбов и лгунов. Правдолюбы говорят правду с вероятностью 80%, а лгуны — с вероятностью 40%. Государство решило подсчитать правдолюбов и лгунов на основе опроса 100 жителей. Каждый раз случайно выбранного человека спрашивают: «Вы лгун?» — и записывают ответ. Однако один человек может поучаствовать в опросе несколько раз. Если житель уже участвовал в опросе — он отвечает то же самое, что и в первый раз. Мы знаем, что правдолюбов 70%, а лгунов 30%. Какая вероятность того, что государство недооценит количество лгунов, т. е. опрос покажет, что лгунов меньше 30%? Дайте ответ в процентах с точкой в качестве разделителя, результат округлите до сотых (пример ввода: 00.00).

Решение

1. Посчитаем вероятность получить ответ «Да» на вопрос «Вы лгун?».

На каждом шаге вероятность получить ответ «Да, я лгун» складывается из вероятности получить «Да» от правдолюбов и вероятности получить «Да» от лгунов.

Посчитаем вероятность получить ответ «Да, я лгун» от правдолюбов:

При первом опросе: вероятность ответа «Да» от правдолюбов * доля правдолюбов = 0,2 * 0,7.
Последующие опросы: вероятность ответа «Да» от правдолюбов * (доля правдолюбов – доля опрошенных правдолюбов) + вероятность ответа «Да» от правдолюбов * (доля опрошенных правдолюбов) = вероятность ответа «Да» от правдолюбов * доля правдолюбов = 0,2 * 0,7.

То есть на каждом шаге вероятность получить ответ «Да, я лгун» от правдолюбов составляет 0,14 и не зависит от того, сколько правдолюбов опросили до этого. Логика аналогична для лгунов.

Таким образом, на каждом шаге вероятность получить ответ «Да, я лгун» равна: 0,2 * 0,7 + 0,4 * 0,3 = 0,26.

2. Посчитаем вероятность недооценить количество лгунов.

Количество лгунов, которое получит государство по результатам опроса, — это биномиальное распределение с параметрами n = 100, p = 0,26.

Необходимо найти вероятность того, что по результатам опроса лгунов в стране окажется меньше 30 (30% от 100 опрошенных): P (x < 30). Для биномиального распределения с параметрами n = 100, p = 0,26 такая вероятность составляет 0,789458. Посчитать можно тут: stattrek.com/online-calculator/binomial.aspx.

Ответ в процентах, округлённых до сотых: 78,95.

B. Театральный сезон и телефоны

^{Решить в Контесте}

Международный сервис по продаже билетов решил подвести итоги театрального сезона. В качестве одной из метрик руководитель проекта хочет посчитать количество пользователей, которые покупали билеты на разные спектакли.

При покупке билета пользователь указывает номер своего телефона. Необходимо найти спектакль с наибольшим числом уникальных телефонных номеров. И посчитать количество соответствующих уникальных телефонных номеров.

Формат ввода

Логи покупок доступны в файле ticket_logs.csv. В первом столбце название спектакля из базы сервиса. Во втором — номер телефона, который оставил пользователь при покупке. Отметим, что в целях конспирации телефонные коды стран заменены на необслуживаемые в настоящий момент зоны.

Формат вывода

Число уникальных номеров.

Решение

Подробный вариант решения лежит в main.py.

Пользователи оставляют телефонные номера в разных форматах. В качестве набора данных берутся случайно сгенерированные номера из необслуживаемых кодов. По данным из Википедии были взяты необслуживаемые зоны 801–807.

Каждый номер может получить одного и более двойников из следующих вариантов:

1. 8-(801)-111-11-11
2. 8-801-111-11-11
3. 8801-111-11-11
4. 8-8011111111
5. +88011111111
6. 8-801-flowers, вместо цифр — буквы (распространено в США)

Как предполагается обнаружить эти особенности:

1. Форматы в пунктах 1–4 видны при первом взгляде на данные и удаляются стандартными методами вроде replace.
2. Формат 5 легко отфильтровать, проверив число символов в телефонах после форматирования пункта 1. Во всех номерах будет 11 символов, кроме этого формата.
3. Пункт 6 самый неочевидный, надо догадаться проверить наличие нечисловых символов в номере телефона. Надеюсь, что смысл этих букв участник быстро найдёт в интернете.

Количество данных относительно небольшое, чтобы при желании можно было даже просмотреть каждую строчку вручную. Найти все шесть форматов можно вообще в первой сотне строк.

C. Рассчитать pFound

^{Решить в Контесте}

В архиве содержится три текстовых файла:

qid_query.tsv — id запроса и текст запроса, разделённые табуляцией;
qid_url_rating.tsv — id запроса, URL документа, релевантность документа запросу;
hostid_url.tsv — id хоста и URL документа.

Нужно вывести текст запроса с максимальным значением метрики pFound, посчитанной по топ-10 документов. Выдача по запросу формируется по следующим правилам:

С одного хоста может быть только один документ на выдаче. Если для запроса есть несколько документов с одним и тем же id хоста — берется максимально релевантный документ (а если несколько документов максимально релевантны, берется любой).
Документы по запросу сортируются по убыванию релевантности.
Если у нескольких документов с разных хостов релевантность одинакова, их порядок может быть произвольным.

Формула для расчёта pFound:

pFound =

$\sum_{i=1}^{10}$ pLook[i] ? pRel[i]
pLook[1] = 1
pLook[i] = pLook[i ? 1] ? (1 ? pRel[i ? 1]) ? (1 ? pBreak)
pBreak = 0,15

Формат вывода

Текст запроса с максимальным значением метрики. Например, для open_task.zip правильный ответ:
гугл переводчик

Решение

Все вводные даны в условии. Что-то дополнительное придумывать не нужно — достаточно аккуратно реализовать вычисление pFound в коде и не забыть взять максимум по хосту. Для решения очень удобно использовать библиотеку pandas — с помощью неё легко группировать по запросам и хостам и вычислять агрегации.

import pandas as pd

# считываем данные
qid_query = pd.read_csv("hidden_task/qid_query.tsv", sep="\t", names=["qid", "query"])
qid_url_rating = pd.read_csv("hidden_task/qid_url_rating.tsv", sep="\t", names=["qid", "url", "rating"])
hostid_url = pd.read_csv("hidden_task/hostid_url.tsv", sep="\t", names=["hostid", "url"])

# делаем join двух таблиц, чтобы было просто брать url с максимальным рейтингом
qid_url_rating_hostid = pd.merge(qid_url_rating, hostid_url, on="url")

def plook(ind, rels):
 if ind == 0:
 return 1
    return plook(ind-1, rels)*(1-rels[ind-1])*(1-0.15)

def pfound(group):
 max_by_host = group.groupby("hostid")["rating"].max() # максимальный рейтинг хоста
 top10 = max_by_host.sort_values(ascending=False)[:10] # берем топ-10 урлов с наивысшим рейтингом
 pfound = 0
    for ind, val in enumerate(top10):
 pfound += val*plook(ind, top10.values)
 return pfound

qid_pfound = qid_url_rating_hostid.groupby('qid').apply(pfound) # группируем по qid и вычисляем pfound
qid_max = qid_pfound.idxmax() # берем qid с максимальным pfound

qid_query[qid_query["qid"] == qid_max]

D. Спортивный турнир

^{Решить в Контесте}

Ограничение по времени на тест	2 с
Ограничение по памяти на тест	256 МБ
Ввод	стандартный ввод или input.txt
Вывод	стандартный вывод или output.txt

Пока Маша была в отпуске, её коллеги организовали турнир по шахматам по олимпийской системе. За отдыхом Маша не обращала особого внимания на эту затею, так что она еле может вспомнить, кто с кем играл (про порядок игр даже речи не идёт). Внезапно Маше пришла в голову мысль, что неплохо бы привезти из отпуска сувенир победителю турнира. Маша не знает, кто победил в финальной игре, но сможет без труда вычислить, кто в нём играл, если только она правильно запомнила играющие пары. Помогите ей проверить, так ли это, и определить возможных кандидатов в победители.

Формат ввода

В первой строке находится целое число 3 ? n ? 2¹⁶ ? 1, n = 2^k ? 1 — количество прошедших игр. В последующих n строках — по две фамилии игроков (латинскими заглавными буквами) через пробел. Фамилии игроков различны. Все фамилии уникальны, однофамильцев среди коллег нет.

Формат ввода

Выведите «NO SOLUTION» (без кавычек), если Маша неправильно запомнила игры, и по этой сетке нельзя получить турнир по олимпийской системе. Если турнирная сетка возможна, выведите две фамилии в одной строке — фамилии кандидатов на первое место (порядок не важен).

Пример 1

Ввод	Вывод
`7 GORBOVSKII ABALKIN SIKORSKI KAMMERER SIKORSKI GORBOVSKII BYKOV IURKOVSKII PRIVALOV BYKOV GORBOVSKII IURKOVSKII IURKOVSKII KIVRIN`	`IURKOVSKII GORBOVSKII`

Пример 2

Ввод	Вывод
`3 IVANOV PETROV PETROV BOSHIROV BOSHIROV IVANOV`	`NO SOLUTION`

Примечания

Олимпийская система, также известная как плей-офф — система организации соревнований, при которой участник выбывает из турнира после первого же проигрыша. Подробнее про олимпийскую систему можно почитать на Википедии.

Схема первого теста из условия:

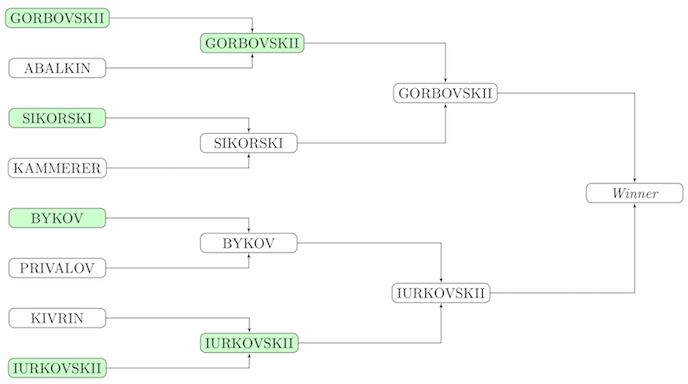
Решение

Из количества игр n = 2^k – 1 легко получить количество раундов турнира k. Обозначим количество игр, которые сыграл i-й участник, через n_i. Очевидно, что финалисты сыграли максимальное количество раз (они единственные играли во всех k раундах). Теперь научимся проверять, что данный нам набор встреч между участниками возможен в турнире по олимпийской системе. Заметим, что игра между участниками i и j могла произойти только в раунде min(n_i, n_j), поскольку этот раунд был последним для кого-то из них (раунды для удобства нумеруются с единицы). Назовём псевдораундом номер r множество игр (i, j), для которых min(n_i, n_j) = r. Проверку корректности будем делать в соответствии с таким утверждением:

Утверждение. Набор из 2^k – 1 игр задаёт турнир по олимпийской системе тогда и только тогда, когда:

1. В каждом псевдораунде все участники различны.
2. Количество игр в псевдораунде r равно 2^{k – r}.

Доказательство. Необходимость этих двух условий очевидна: псевдораунды соответствуют настоящим раундам турнира, а для настоящих раундов условия верны. Достаточность докажем индукцией по k. При k = 1 есть одна игра с двумя различными участниками — это корректный олимпийский турнир. Проверим переход k – 1 -> k.

Во-первых, докажем, что каждый участник турнира играл в первом псевдораунде. Рассмотрим произвольного игрока, пусть он участвовал в q играх. В каждом псевдораунде он мог сыграть не более одного раза, причём в псевдораундах после q-го он не мог играть ни разу. Значит, он должен был сыграть по одному разу в каждом из псевдораундов 1, 2, ..., q. Это, в частности, означает, что все люди сыграли в первом псевдораунде, а всего игроков 2^k. Теперь докажем, что в каждой из 2^{k – 1} игр первого псевдораунда был ровно один участник с n_i = 1. Как минимум один такой участник в каждой игре должен быть по определению псевдораунда.

С другой стороны, есть не менее 2^{k – 1} человек с n_i > 1 — это участники следующего псевдораунда. Следовательно, людей с n_i = 1 было ровно 2^{k – 1}, по одному на каждую игру. Теперь легко понять, как должен выглядеть первый раунд искомого турнира: назначим в каждой игре первого псевдораунда проигравшим участника с n_i = 1, а победителем — участника с n_i > 1. Множество игр между победителями удовлетворяет условию для k – 1 (после выбрасывания игр из первого псевдораунда все n_i уменьшились на 1). Следовательно, этому множеству соответствует турнир по олимпийской системе.

import sys
import collections

def solve(fname):
    games = []
    for it, line in enumerate(open(fname)):
        line = line.strip()
        if not line:
            continue
        if it == 0:
            n_games = int(line)
            n_rounds = n_games.bit_length()
        else:
            games.append(line.split())

    gamer2games_cnt = collections.Counter()
    rounds = [[] for _ in range(n_rounds + 1)]

    for game in games:
        gamer_1, gamer_2 = game
        gamer2games_cnt[gamer_1] += 1
        gamer2games_cnt[gamer_2] += 1

    ok = True
    for game in games:
        gamer_1, gamer_2 = game
        game_round = min(gamer2games_cnt[gamer_1], gamer2games_cnt[gamer_2])
        if game_round > n_rounds:
            ok = False
            break
        rounds[game_round].append(game)

    finalists = list((gamer for gamer, games_cnt in gamer2games_cnt.items() if games_cnt == n_rounds))

    for cur_round in range(1, n_rounds):
        if len(rounds[cur_round]) != pow(2, n_rounds - cur_round):
            ok = False
            break
        cur_round_gamers = set()
        for gamer_1, gamer_2 in rounds[cur_round]:

            if gamer_1 in cur_round_gamers or gamer_2 in cur_round_gamers:
                ok = False
                break
            cur_round_gamers.add(gamer_1)
            cur_round_gamers.add(gamer_2)

    print ' '.join(finalists) if ok else 'NO SOLUTION'

def main():
    solve('input.txt')

if name == '__main__':
    main()

Чтобы порешать задачи других треков чемпионата, нужно зарегистрироваться здесь.

Где порешать аналитические задачи от команд Яндекса? Контест и разбор +24

A. Посчитать лгунов в стране

B. Театральный сезон и телефоны

C. Рассчитать pFound

D. Спортивный турнир

Комментарии (0)