Эта статья внеплановая. В прошлый раз я рассматривал нюансы и проблемы различных методов нормализации данных. И только после публикации понял, что не упомянул некоторые важные детали. Кому-то они покажутся очевидными, но, по-моему, лучше сказать об этом явно.

Нормализация категориальных данных

Чтобы не засорять текст базовыми вещами, я буду считать, что Вы знаете, что такое категориальные и порядковые данные, и чем они отличаются от остальных.

Очевидно, что любая нормализация может выполняться только для числовых данных. Соответственно, если для дальнейшей работы Вашему алгоритму/программе подходят только числа, то необходимо преобразовать все остальные типы к ним.

С категориальными данными всё просто. Если целью является не просто кодировка (шифровка) значений какими-то числами, то единственный доступный вариант — это представить их в виде значений “1” — “0” (ДА — НЕТ) для каждой возможной категории. Это так называемое one-hot-кодирование. Когда вместо одного категориального признака появится столько новых “булевых” признаков, сколько существует возможных категорий.

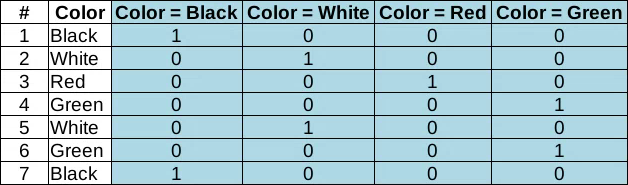
И всё.

Никаких вычислений медиан или средних арифметических, никаких смещений.

Если Вы подготавливаете данные для входа нейронной сети, это именно то, что нужно.

Важно понять, что применять преобразования подобные стандартизации к категориальным/”булевым” признакам как минимум бесполезно, а как максимум — вредно. Поскольку может необоснованно увеличить или уменьшить их интервал значений. Подробнее о важности равенства этих интервалов я писал в прошлый раз.

К тому же, если Вы хотите получить результат, основанный на данных, а не на внутренних особенностях алгоритмов, то даже после преобразования в числовую форму категориальные признаки нельзя использовать как обычные числовые для вычисления “расстояний” между объектами или их “схожести”. Если два объекта отличаются только “наличием черного цвета”, это не значит, что между ними “расстояние” равное некому безразмерному единичному интервалу. Это значит именно то, что у одного есть чёрный цвет, а у другого его нет — и не более того.

Конечно, какой-то результат Вы получите всегда, даже при подходе «не хочу мудрить, пусть будут просто числа 0 и 1». Сомнительный, но получите. Как корректно работать с такими данными, я подробно напишу в следующей статье.

Нормализация порядковых данных

С порядковыми данными немного сложнее. Они занимают “промежуточное” положение между категориальным и относительным (обычными числами) типами данных. И при работе с ними необходимо сделать выбор, к какому из соседних типов их преобразовывать. Без Вашего осознанного решения здесь никак.

Вариант 1. Из порядковых в категориальные. В этом случае теряется информация о порядке значений (что больше). Но если это не является (по Вашему мнению) важным фактором, и особенно, когда возможных значений немного, то вполне приемлемо. На выходе получаем набор категорий, с которыми дальше работаем, как описано выше.

Вариант 2. Преобразование в интервальный тип (обычные числа). В этом случае сохраняется порядок значений, но “добавляется” необоснованная информация о величине разницы между двумя значениями.

До преобразования Вы знали, какие значения больше других, но не могли сказать насколько больше. После — это станет возможным, хотя, повторюсь, без всякого обоснования.

Дальше работаем как с обычными значениями — нормируем и т.д.

“Парные” признаки

Формально такого понятия, конечно, не существует. Я так обозначаю редкую, но заслуживающую внимания ситуацию.

Для начала определение. “Парными” признаками я называю признаки, которые измеряются в одинаковых единицах и вместе описывают единый комбинированный признак. Причем изменения по любому из таких “напарников” равнозначны.

Проще пояснить на примере. Представьте, что у Вас есть набор данных о строениях, размещенных на одной улице города, которая лежит строго с юга на север. Данные самые разные — тип, размер, количество жильцов, цвет и координаты (широта и долгота). И перед Вами стоит задача провести кластерный анализ для выявления групп похожих строений.

“Парными” признаками здесь являются широта и долгота, которые вместе составляют единый признак “координаты”. Временно забудем про остальные признаки и присмотримся к координатам.

Для кластеризации важно определять расстояние между двумя объектами. В нашем случае расстояние рассчитывается по их координатам. И совершенно одинаково, например, отстоит детский садик от стадиона на 100 м вдоль по улице, или он в тех же 100 м через дорогу. Это одинаковые 100 м.

Если на этот нюанс не обращать внимания, то после нормализации ситуация станет такой

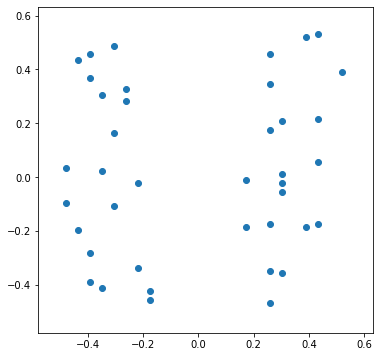
Изначальный смысл совершенно исказился. “Расстояние” между зданиями, расположенными через дорогу стало практически таким же большим, как и между домами в начале и конце улицы. Это произошло из-за того, что значения широты и долготы были нормализированы независимо друг от друга.

Решение этой проблемы лежит в определении параметров масштабирования самого “протяженного” признака (в нашем случае долготы) и применения его к всем “парным” признакам.

Да, формально, мы снизили влияние признака “широта”. Но это было обусловлено его реальным физическим смыслом.

Правила безопасности

“Назначать” признаки в “парные” нужно очень осторожно и с четким пониманием исследуемой области.

Возьмем другой пример. Вы анализируете колебания некоего узла/датчика, закрепленного на вертикальном элементе в большом механизме. У Вас есть величины колебаний как “вправо-влево” (синие стрелки), так и “вперёд-назад” (оранжевые стрелки). Еще, из-за конструктивных особенностей механизма, колебания “вправо-влево” могут быть в несколько раз больше, чем “вперёд-назад”.

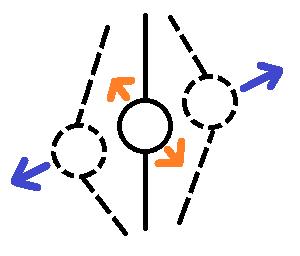
Вроде бы ситуация схожая с прошлой. Оба признака измеряются в миллиметрах. И вместе они составляют условные “координаты” узла при его колебаниях.

Но, допустим, оказывается (из-за тех же конструктивных особенностей), что сильные колебания “вперёд-назад”, пусть даже они по величине в разы меньше, чем “вправо-влево”, могут привести к поломке узла. Т.е. величина изменения у этого признака не равнозначна его “напарнику”.

В этом случае снижать влияние этого признака, как мы выше поступили с “широтой”, наоборот нельзя.

В общем, напоследок банальный совет — перед тем как начать какие-либо преобразования своих данных, не забудьте внимательно к ним присмотреться. Вдруг среди них есть что-то требующее чуть более индивидуального подхода.

P.S. — для тех, кому интересно пробовать класс-демонстратор AdjustedScaler, я внес необходимые дополнения для случая “парных” признаков.