«То что ясно всем, ещё кто-то должен сказать»
Типа эпиграфа, Google/Яндекс автора не сыскали
Это вторая часть статьи «То что ясно всем».
Для лучшего понимания изложенного в ней алгоритма Z добавлю здесь удачный пример, приведённый ранее в обсуждении/комментах.
Представьте себе, что стоит задача построить кривую некоей функции Т(Х) на заданном интервале (допустимых) значений. Сделать это желательно максимально подробно, но вы заранее не знаете, когда вас «схватят за руку». Вы хотите генерировать значения Х так, чтобы в любой момент, когда прервётся построение кривой (генерация параметров Х на интервале и вычисление Т(Х)), получившийся график максимально точно отражал эту функцию. Окажется больше времени — график будет точнее, но — всегда максимум из возможного на данный момент для произвольной функции.
Конечно, для известной функции алгоритм разбиения интервала может учитывать её поведение, но здесь речь идёт об общем подходе, дающем искомый результат с минимальными «потерями». Для двумерного случая можно привести пример отображения некоего рельефа/поверхности и желать быть уверенным, что сколько успели — отобразили максимум его особенностей.
Задача и объекты моделирования (из первой части) в общем случае могут сильно различаться: есть теоретическая/физическая модель или приближение или нет этого (чёрный ящик) — везде будут свои нюансы в построении моделей. Но необходимость генерации параметров (в т.ч. алгоритм Z) — общая и неотъемлемая часть для всех. Есть объекты (например такие), когда время на получение Т слишком велико (дни и недели), тогда алгоритм выбора нового шага останавливается по другим критериям, не по причине завершения цикла основного расчёта в параллельном процессе. Нет смысла далее уменьшать шаг для улучшения поиска следующего прогноза Т, если ожидаемое улучшение заведомо хуже погрешности модели и/или ошибок измерения Т.
Приведу ещё одну иллюстрацию разбиения допустимого интервала для двумерного случая алгоритма Z (K = 3 на поле 64*64):

Точки, выделенные на рисунке (9 шт.) — это начальные точки краёв и середины интервала, они, если это необходимо, считаются вне алгоритма Z. Можно заметить, что по горизонтальным и вертикальным направлениям/«дорожкам», соединяющим эти точки, генерируемые алгоритмом Z значения не попадают. Дополнительные точки тут несложно рассчитать отдельно, но с ростом числа точек вдоль этих направлений/«дорожек» представление функции будет улучшаться («дорожки» становятся уже) и необходимости дополнять сам алгоритм (надо 7 строк, из них 4 оператора в основном цикле по n, см. ниже) или создавать отдельный расчёт я не вижу. Тем более, что в этом случае ухудшается средняя эффективность алгоритма, а особого улучшения представления модели не будет (уже при n > 8 шаг по параметру меньше 1/1000, см. таблицу ниже).
Второй особенностью алгоритма Z является (для двумерного случая) несимметрия порядка добавления точек — по оси/параметру Y они в среднем чаще, картина выравнивается в конце каждого цикла по n.
Алгоритм Z, одномерный случай, на языке VBA:
Алгоритм Z, двумерный случай, язык VBA:
Вычислительные затраты:
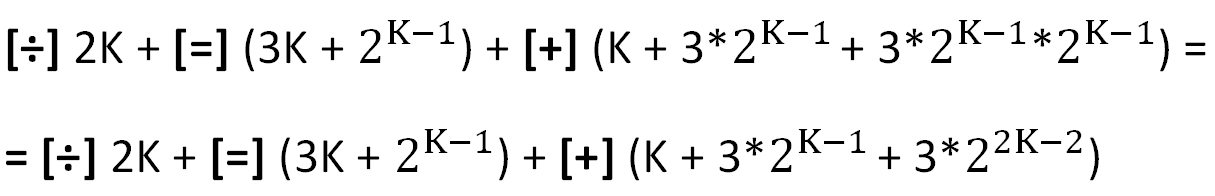
В квадратных скобках обозначены основные операции, используемые в расчётах (затраты на организацию циклов не учитываются).
Здесь надо заметить, что достаточно «тяжёлая» операция деления [?] в данном случае не является затратной, ибо целочисленное деление на 2 — это сдвиг на один разряд. Относительные затраты на операцию деления и присваивания ([=], второе слагаемое) с ростом K быстро стремятся к нулю.
Всего точек:

Средние затраты:

Для первых значений K проведём расчёты по этим формулам и заполним таблицу:

Здесь «доля интервала» — относительный шаг между точками в конце цикла по n.
Последняя строка («среднее») показывает относительные затраты на точку — долю сложений/вычитаний. Предел стремится к 0,5625 или 1/1,77777 операции сложения.
Возвращаясь к утверждению из первой части статьи, здесь показано что «предлагаемый к обсуждению алгоритм демонстрирует предельно малые вычислительные затраты и не влечёт недостатков или сложностей», а в условиях внезапного прерывания вычислений дополнительно имеет преимущества. Разумно его использовать во всех подходящих применениях.
Прошу помощи в распространении и внедрении как в программном, так и аппаратном исполнении.
Типа эпиграфа, Google/Яндекс автора не сыскали
Это вторая часть статьи «То что ясно всем».
Для лучшего понимания изложенного в ней алгоритма Z добавлю здесь удачный пример, приведённый ранее в обсуждении/комментах.
Представьте себе, что стоит задача построить кривую некоей функции Т(Х) на заданном интервале (допустимых) значений. Сделать это желательно максимально подробно, но вы заранее не знаете, когда вас «схватят за руку». Вы хотите генерировать значения Х так, чтобы в любой момент, когда прервётся построение кривой (генерация параметров Х на интервале и вычисление Т(Х)), получившийся график максимально точно отражал эту функцию. Окажется больше времени — график будет точнее, но — всегда максимум из возможного на данный момент для произвольной функции.
Конечно, для известной функции алгоритм разбиения интервала может учитывать её поведение, но здесь речь идёт об общем подходе, дающем искомый результат с минимальными «потерями». Для двумерного случая можно привести пример отображения некоего рельефа/поверхности и желать быть уверенным, что сколько успели — отобразили максимум его особенностей.
Задача и объекты моделирования (из первой части) в общем случае могут сильно различаться: есть теоретическая/физическая модель или приближение или нет этого (чёрный ящик) — везде будут свои нюансы в построении моделей. Но необходимость генерации параметров (в т.ч. алгоритм Z) — общая и неотъемлемая часть для всех. Есть объекты (например такие), когда время на получение Т слишком велико (дни и недели), тогда алгоритм выбора нового шага останавливается по другим критериям, не по причине завершения цикла основного расчёта в параллельном процессе. Нет смысла далее уменьшать шаг для улучшения поиска следующего прогноза Т, если ожидаемое улучшение заведомо хуже погрешности модели и/или ошибок измерения Т.
Приведу ещё одну иллюстрацию разбиения допустимого интервала для двумерного случая алгоритма Z (K = 3 на поле 64*64):

Точки, выделенные на рисунке (9 шт.) — это начальные точки краёв и середины интервала, они, если это необходимо, считаются вне алгоритма Z. Можно заметить, что по горизонтальным и вертикальным направлениям/«дорожкам», соединяющим эти точки, генерируемые алгоритмом Z значения не попадают. Дополнительные точки тут несложно рассчитать отдельно, но с ростом числа точек вдоль этих направлений/«дорожек» представление функции будет улучшаться («дорожки» становятся уже) и необходимости дополнять сам алгоритм (надо 7 строк, из них 4 оператора в основном цикле по n, см. ниже) или создавать отдельный расчёт я не вижу. Тем более, что в этом случае ухудшается средняя эффективность алгоритма, а особого улучшения представления модели не будет (уже при n > 8 шаг по параметру меньше 1/1000, см. таблицу ниже).
Второй особенностью алгоритма Z является (для двумерного случая) несимметрия порядка добавления точек — по оси/параметру Y они в среднем чаще, картина выравнивается в конце каждого цикла по n.
Алгоритм Z, одномерный случай, на языке VBA:
Xmax =
Xmin =
Dx = (Xmax - Xmin) / 2
L = 2
Sx = 0
For n = 1 To K
Dx = Dx / 2
D = Dx
For j = 1 To L Step 2
X = Xmin + D
Cells(5, X) = "O" 'здесь и ниже - вызов/расчёт модели T(X)
X = Xmax - D
Cells(5, X) = "O"
D = D + Sx
Next j
Sx = Dx
L = L + L
Next nАлгоритм Z, двумерный случай, язык VBA:
Xmax = ' 65 - значения для примера выше, GIF
Xmin = ' 1
Ymax = ' 65
Ymin = ' 1
Dx = (Xmax - Xmin) / 2
Dy = (Ymax - Ymin) / 2
L = 2
Sx = 0
Sy = 0
For n = 1 To K ' K = 3 для примера GIF
Dx = Dx / 2
Dy = Dy / 2
Tx = Dx
For j = 1 To L Step 2
X1 = Xmin + Tx
X2 = Xmax - Tx
Ty = Dy
For i = 1 To L Step 2
Y = Ymin + Ty
Cells(Y, X1) = "O" 'здесь и ниже - вызов/расчёт модели T(Y,X)
Cells(Y, X2) = "O"
Y = Ymax - Ty
Cells(Y, X1) = "O"
Cells(Y, X2) = "O"
Ty = Ty + Sy
Next i
Tx = Tx + Sx
Next j
Sx = Dx
Sy = Dy
L = L + L
Next nВычислительные затраты:
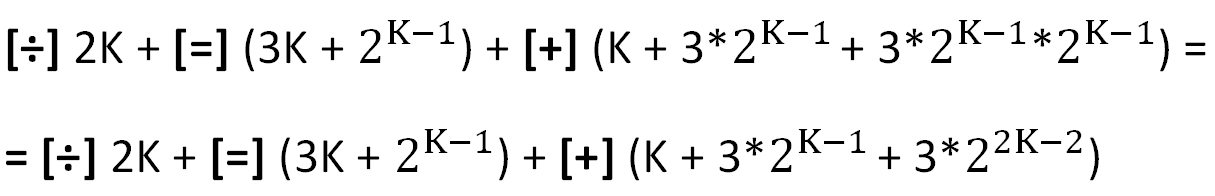
В квадратных скобках обозначены основные операции, используемые в расчётах (затраты на организацию циклов не учитываются).
Здесь надо заметить, что достаточно «тяжёлая» операция деления [?] в данном случае не является затратной, ибо целочисленное деление на 2 — это сдвиг на один разряд. Относительные затраты на операцию деления и присваивания ([=], второе слагаемое) с ростом K быстро стремятся к нулю.
Всего точек:

Средние затраты:

Для первых значений K проведём расчёты по этим формулам и заполним таблицу:

Здесь «доля интервала» — относительный шаг между точками в конце цикла по n.
Последняя строка («среднее») показывает относительные затраты на точку — долю сложений/вычитаний. Предел стремится к 0,5625 или 1/1,77777 операции сложения.
Возвращаясь к утверждению из первой части статьи, здесь показано что «предлагаемый к обсуждению алгоритм демонстрирует предельно малые вычислительные затраты и не влечёт недостатков или сложностей», а в условиях внезапного прерывания вычислений дополнительно имеет преимущества. Разумно его использовать во всех подходящих применениях.
Прошу помощи в распространении и внедрении как в программном, так и аппаратном исполнении.

