В этой статье я расскажу о том как у меня возникла идея написать свой тюнер и к чему это привело. А так же поделюсь своими скромными знаниями в области ЦОС (цифровой обработки сигналов) полученными в ВУЗе, и как они помогли мне решить некоторые проблемы. И конечно, поделюсь исходным кодом и опытом программирования на Swift который получил при реализации этого проекта.

Предыстория

Идея написать свой тюнер для гитары у меня возникла довольно давно, ещё лет 10 назад когда я учился в университете. К тому имелось ряд причин:

• Во–первых, не так то уж много действительно качественных программ–тюнеров — некоторые просто неправильно определяют частоту, либо работают крайне неустойчиво на верхних струнах. Кроме этого, все тюнеры, которые мне попадались, a priori настраиваются на A440 (когда ля первой октавы настраивается на 440 Гц). Но есть ещё настройка на C256 (до первой октавы настраивается на 256 Гц). Многие тюнеры не позволяют настраиваться на ладах, хотя если нужно играть на 5-7 ладу, лучше настраивать инструмент на этих же ладах.
• Во–вторых, визуализация настройки в виде ползунка, спектра или частотной осциллограммы, на мой взгляд, немного не физичны. Мне хотелось показать как выглядит волна порождаемая инструментом непосредственно — насколько она чистая, или наоборот искажённая. Сделать визуализацию наглядной и отзывчивой.
• В–третьих, хотелось применить на пользу человечества свои знания в области в ЦОС, полученные в ВУЗе.

В общем, идея долго сидела у меня в голове, но реализовать её получилось только в этом году, как наконец-таки появилось свободное время, iOs-устройство и некоторый опыт мобильной разработки.

Немного теории

Любой человек немного знакомый с европейскими струнными инструментами знает, что каждая струна настраивается на некоторую ноту, а этой ноте соответствует некоторая частота. Разница между нотой и частотой в том, что каждая нота несёт в себе некоторую музыкальную функцию. И эта функция определяется положением ноты относительно других нот, так например нота до в последовательности до-мажор играет роль тоники, т.е. основного и самого устойчивого звука. Если эта нота немного сдвинется, то она потеряет свою функцию. Для того что бы извлекаемые звуки соответствовали нотам требуется соблюдать строгое соответствие между интервалами нот и соотношением частот. От точности и стабильности частоты порождаемой струной будет зависеть соответствие извлечённого звука той функции что была заложена в ноту.

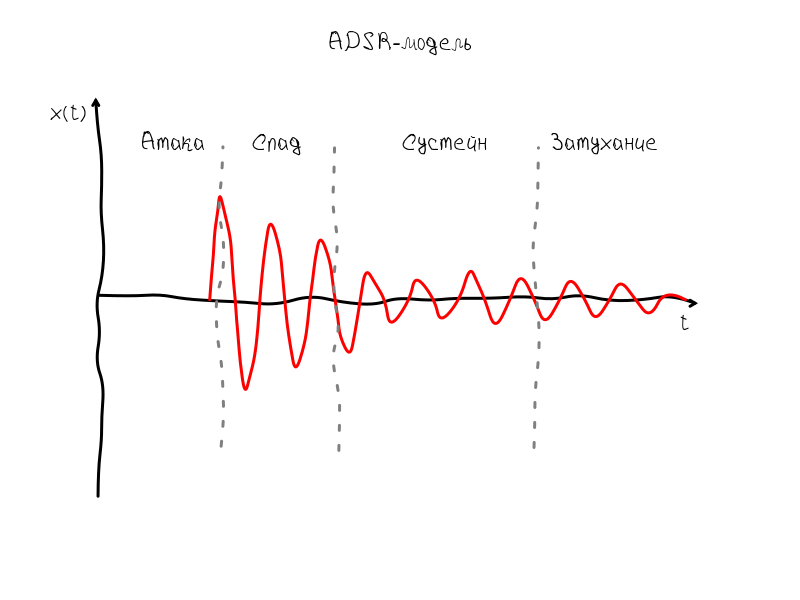
Что же представляет из себя звук порождаемый струнной? Если воспользоваться ADSR моделью, которую предложил американский исследователь и композитор Владимир Усачевский для первых синтезаторов, то звук струны представляет собой модулированное некоторой огибающей гармоническое колебание. Эта огибающая получила название ADSR, т.к. она имеет четыре характерных момента: атаку (англ. attack), спад (англ. decay), сустейн (англ. sustain) и затухание (англ. release).



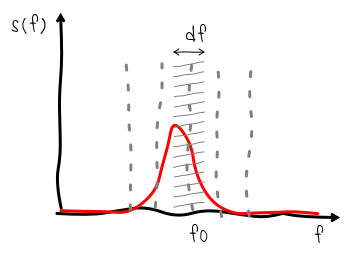
Интервал сустейна наиболее чётко передаёт частоту, т.к. колебания происходят практически без изменения амплитуды. Если бы гитара порождала идеальный моногармонический звук, то с учётом ADSR-огибающей спектр такого колебания имел бы вид узкой полоски. Форма бы этой полоски соответствовала спектру огибающей:



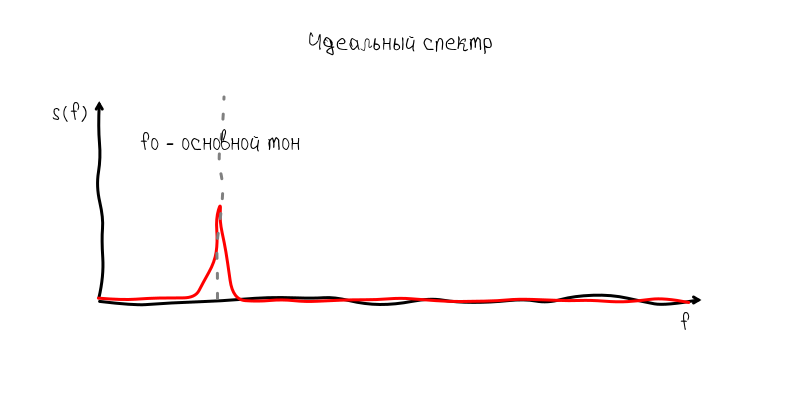
Но реальный инструмент порождает нелинейные колебательные процессы, в результате чего появляются дополнительные гармоники, которые называют обертонами.



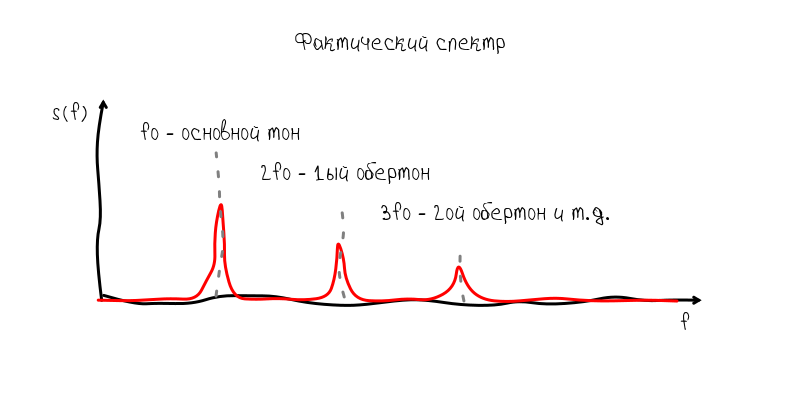
Эти обертоны являются довольно коварными попутчиками, т.к. они могут превалировать над основным тоном и мешать определению частоты. Но всё-же, обычно основной тон хорошо определяется без дополнительных манипуляций.

Итак, на основе этих представлений можно наметить путь по которому должна работать программа:

1. Вычислить преобразование Фурье звуковой волны
2. Найти основной тон на спектре
3. Вычислить частоту основного тона

О стоячих волнах

Обычно звук на графике представляют в виде развёртки по времени. В точке нуль по оси абсцисс располагается значение в начальный момент наблюдения, далее соответственно значения которые будут наблюдаться через 1 с, 2 с и т.д. Процесс измерения в таком случае можно представить воображаемой рамкой, которая равномерно движется слево на право. Эта рамка может называться по разному: окном наблюдения (англ. observation window), интервалом наблюдения (англ. observation interval), временным окном (англ. time window) — все эти термины означают примерно одно и тоже.



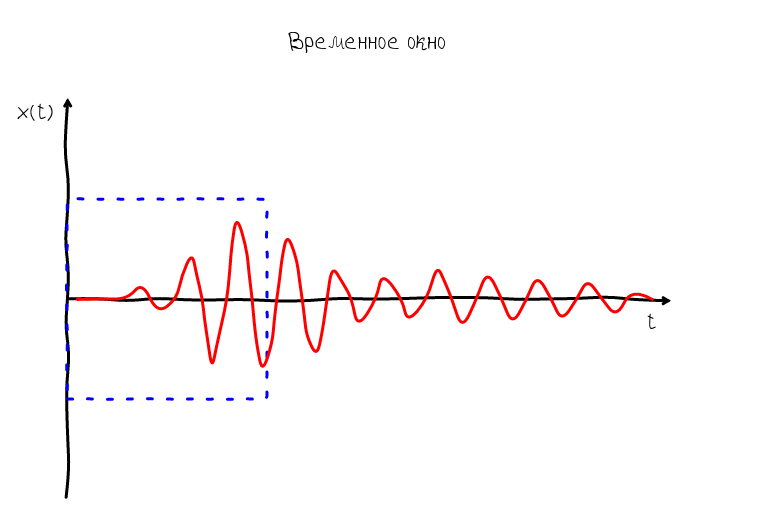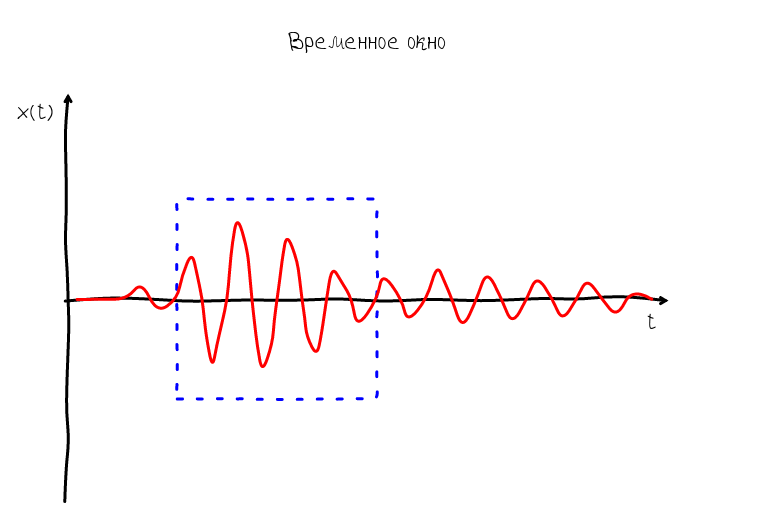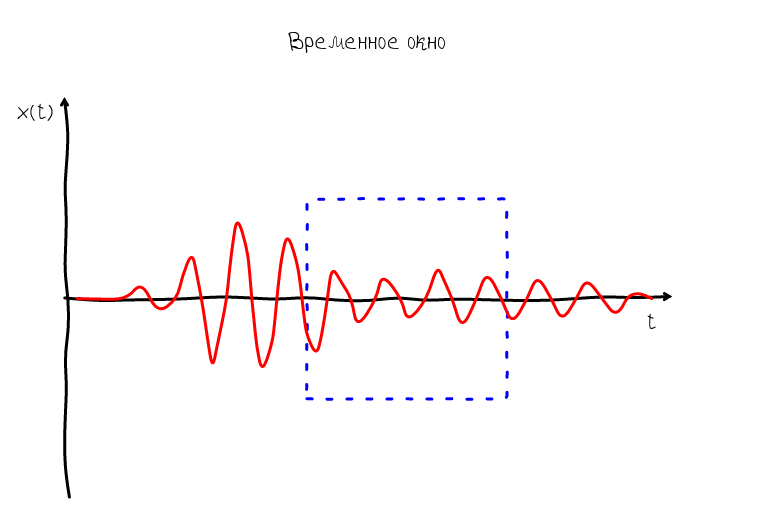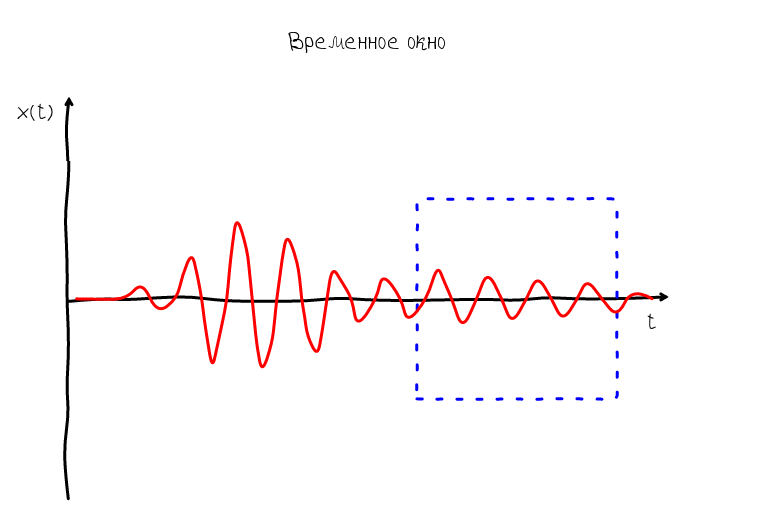
Итак, рамка даёт нам понять как происходит процесс измерения и какие моменты оказываются в начале рамки, а какие в конце. На основе этого мы можем представить что будет если сопоставить систему координат с рамкой — у нас возникнет ощущение, что звуковая волна появляется в правой части графика и исчезает в левой. Такая волна называется бегущей:



Но такое представление звуковой волны не информативно, т.к. волна может двигаться очень и очень быстро. Наша задача каким-то образом остановить волну. Для того что бы волна остановилась нужно что бы её скорость была равно 0. А т.к. у волны есть две скорости: фазовая и групповая, то можно получить два вида стоячих волн:



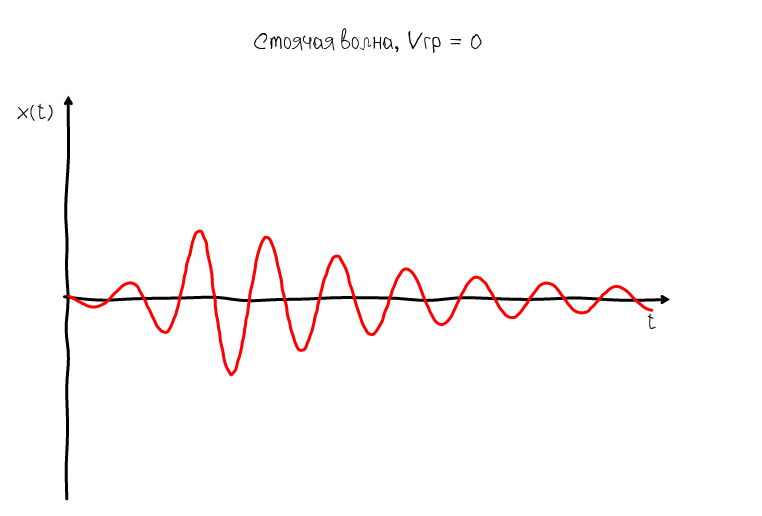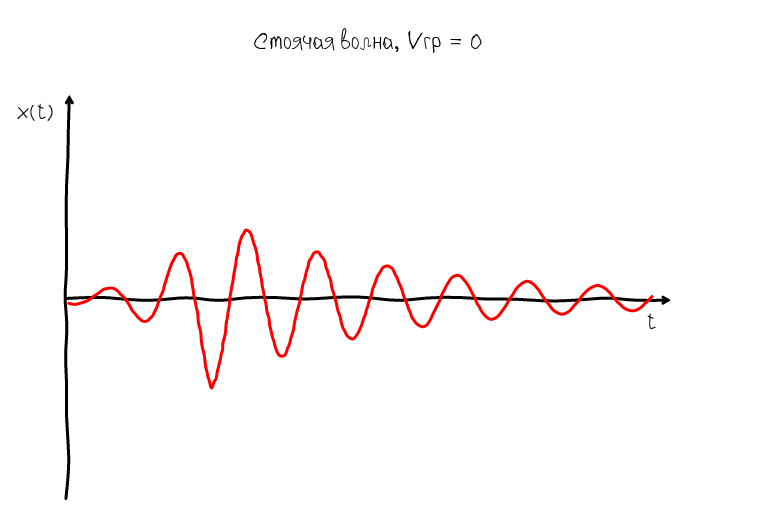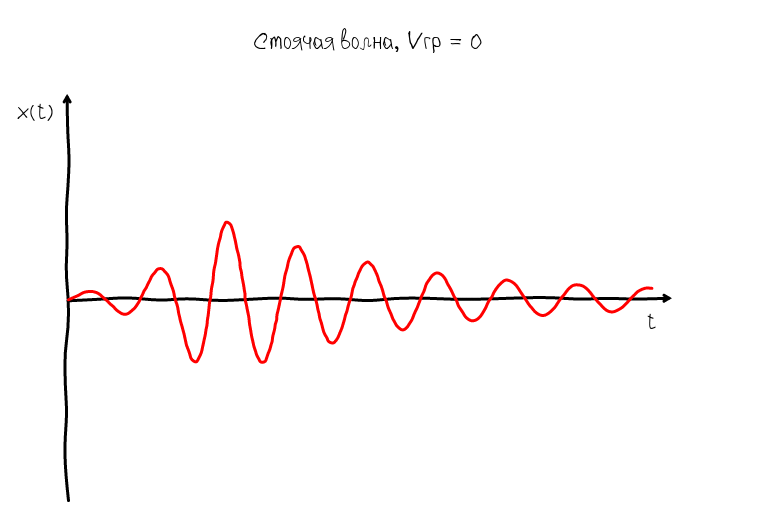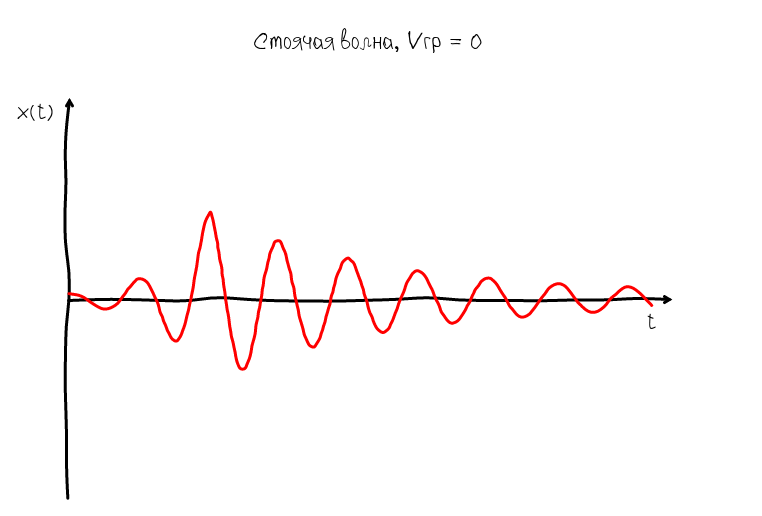
Стоячая волна у которой групповая скорость равна нулю характеризуется тем, что её огибающая остаётся всегда на одном месте. Но при этом колебания не останавливаются — нули и горбики продолжают двигаться вдоль оси абсцисс. Очевидно, что такая волна нам не подходит, т.к. интерес представляет то что происходит внутри ADSR-огибающей, а именно в момент когда мы наблюдаем колебания в режиме сустейна.

Для этого есть другой тип стоячих волн, у которых фазовая скорость равна нулю:



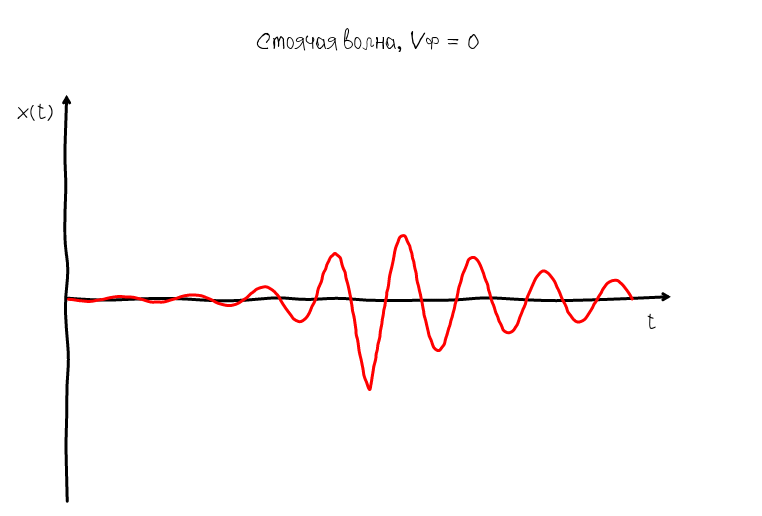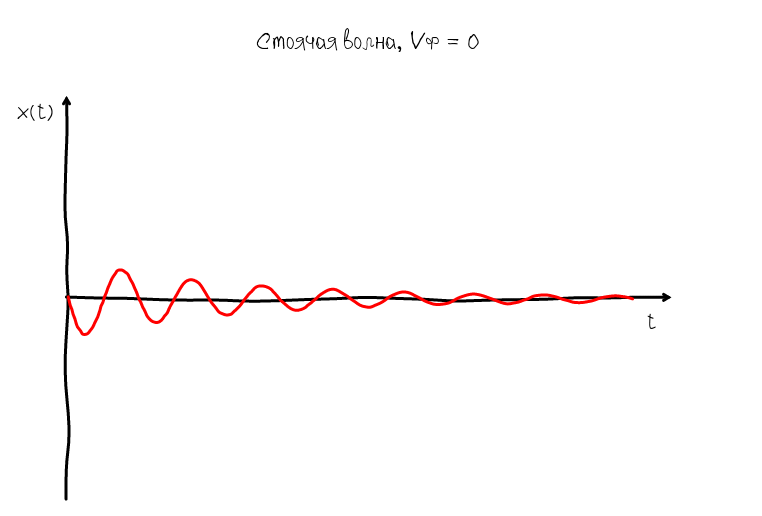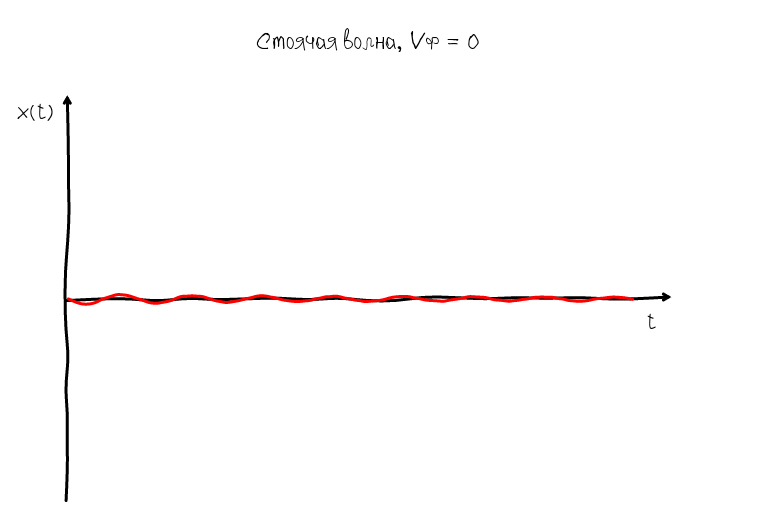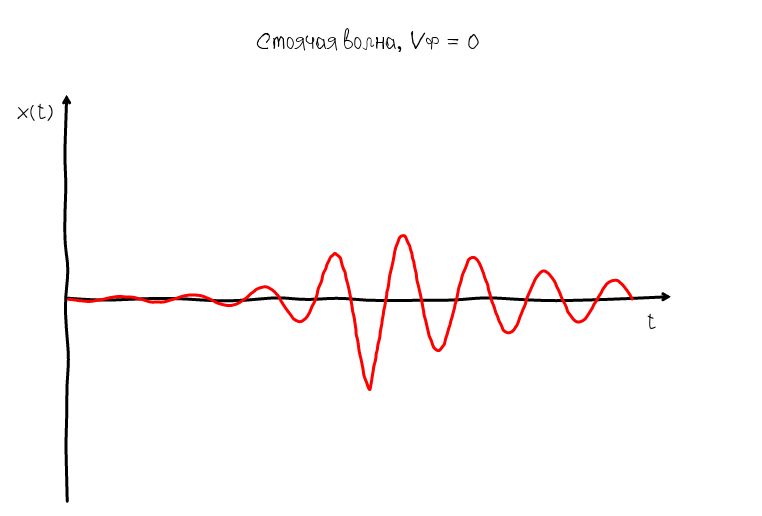
Нулевая фазовая скорость гарантирует что узлы и горбики всегда остаются на одном месте, поэтому мы можем легко разглядеть форму гармонического колебания и оценить насколько оно близко к идеальной синусоидальной форме. Алгоритм получения такой волны очевиден:

1. Найти фазу основного тона
2. Сместить отображаемую волну на величину фазы

Реализация

Запись с микрофона

Вообще-то Apple предоставляет много высокоуровневых возможностей для работы с мультимедиа из Objective-C/Swift. Но по сути теперь работа со звуком крутиться вокруг Audio Queue Services:

Audio Queue Services provides features similar to those previously offered by the Sound Manager and in OS X. It adds additional features such as synchronization. The Sound Manager is deprecated in OS X v10.5 and does not work with 64-bit applications. Audio Queue Services is recommended for all new development and as a replacement for the Sound Manager in existing Mac apps.
источник

Но в отличие от SoundManager'а который был довольно-таки высокоуровневым решением, Audio Queue Services это корявые обёртки которые просто повторяют C-код на Swift:

    func AudioQueueNewInput(_ inFormat: UnsafePointer<AudioStreamBasicDescription>,
                      _ inCallbackProc: AudioQueueInputCallback,
                      _ inUserData: UnsafeMutablePointer<Void>,
                      _ inCallbackRunLoop: CFRunLoop!,
                      _ inCallbackRunLoopMode: CFString!,
                      _ inFlags: UInt32,
                      _ outAQ: UnsafeMutablePointer<AudioQueueRef>) -> OSStatus

Профита от низкоуровневого кода в Swift нет, поэтому захват звука я оставил на откуп вспомогательному C-коду. Если опустить второстепенный код для управления буферами, то настройка записи заключается в инициализации структуры AQRecorderState с помощью функции AudioQueueNewInput:

    void AQRecorderState_init(struct AQRecorderState* aq, double sampleRate, size_t count){
        aq->mDataFormat.mFormatID = kAudioFormatLinearPCM;
        aq->mDataFormat.mFormatFlags = kLinearPCMFormatFlagIsPacked | kLinearPCMFormatFlagIsSignedInteger;
        aq->mDataFormat.mSampleRate = sampleRate;
        aq->mDataFormat.mChannelsPerFrame = 1;
        aq->mDataFormat.mBitsPerChannel = 16;
        aq->mDataFormat.mFramesPerPacket = 1;
        aq->mDataFormat.mBytesPerPacket = 2;// for linear pcm
        aq->mDataFormat.mBytesPerFrame = 2;

        AudioQueueNewInput(&aq->mDataFormat, HandleInputBuffer, aq, NULL, kCFRunLoopCommonModes, 0, &aq->mQueue);

        DeriveBufferSize(aq->mQueue,
                         &aq->mDataFormat,
                         (double)count / sampleRate,  // seconds
                         &aq->bufferByteSize);

        for (int i = 0; i < kNumberBuffers; ++i) {
            AudioQueueAllocateBuffer(aq->mQueue, aq->bufferByteSize, &aq->mBuffers[i]);
            AudioQueueEnqueueBuffer(aq->mQueue, aq->mBuffers[i], 0, NULL);
        }

        aq->mCurrentPacket = 0;
        aq->mIsRunning = true;

        aq->buffer = Buffer_new(32768);
        aq->preview_buffer = Buffer_new(5000);

        AudioQueueStart(aq->mQueue, NULL);
    }

Запись данных происходит через функцию HandleInputBuffer. Вызовы Buffer_write_ints преобразует данные из int во float и сохраняет в буфер для дальнейшей обработки.

    static void HandleInputBuffer (
        void                                 *aqData,
        AudioQueueRef                        inAQ,
        AudioQueueBufferRef                  inBuffer,
        const AudioTimeStamp                 *inStartTime,
        UInt32                               inNumPackets,
        const AudioStreamPacketDescription   *inPacketDesc
    ) {
        struct AQRecorderState* pAqData = (struct AQRecorderState*)aqData;

        if(inNumPackets == 0 && pAqData->mDataFormat.mBytesPerPacket != 0)
            inNumPackets = inBuffer->mAudioDataByteSize / pAqData->mDataFormat.mBytesPerPacket;

        const SInt16* data = inBuffer->mAudioData;
        Buffer_write_ints(pAqData->buffer, data, inNumPackets);
        Buffer_write_ints(pAqData->preview_buffer, data, inNumPackets);

        if (pAqData->mIsRunning == 0) return;

        AudioQueueEnqueueBuffer(pAqData->mQueue, inBuffer, 0, NULL);
    }

Проблемы производительности и Swift

Первоначально идея заключалась в том, что бы на 100% использовать язык Swift. В общем-то так я поступил, переписал весь код на Swift за исключением FFT для которого использовалась реализация из библиотеки Accelerate. Но как ни странно, версия на Swift выдала огромнейшую нагрузку в районе 95% процессорного времени и задержку в обработке сигнала которая приводила к ужасно медленной отрисовки.

В таком виде конечно же приложение не было пригодно к использованию, поэтому пришлось всю обработку сигнала полностью переводить на библиотеку Accelerate. Но даже после этого нагрузка всё равно оставалось высокой. Пришлось перенести на C и те операции с массивами которые требовали всего лишь одного прохода, т.е. линейного времени исполнения. Для иллюстрации приведу идентичный код на Swift и C:

    class Processing{
        ...
        func getFrequency() -> Double {
            var peak: Double = 0
            var peakFrequency: Double = 0

            for i in 1..<spectrum.count/2 {
                var spectrumValue: Double = p->spectrum[i]
                var f: Double = fd * i / spectrum.count

                if (spectrumValue > peak) {
                    peak = spectrum[i]
                    peakFrequency = f
                }
            }
            return peakFrequency
        }
    }

    double get_frequency(p* processing){
        double peak = 0;
        double peakFrequency = 0;

        for(size_t i = 1; i < p.spectrumLength / 2; i ++){
            double spectrumValue = p->spectrum[i];
            double f = p->fd * i / p->spectrumLength;

            if (spectrumValue > peak) {
                peak = spectrum;
                peakFrequency = f;
            }
        }

        return peakFrequency;
    }

Вобщем, даже тривиальный проход по массиву, если он делается в цикле с частотой 20 вызовов в секунды смог довольно сильно загрузить устройство.

Возможно это была проблема первой версии Swift, но в итоге пришлось полностью исключить из Swift всё что производило поэлементные операции. Так что в Swift остался только отвечающий за создание массивов, передача в вспомогательные библиотеки написанные на C, а так же код отрисовки на OpenGL ES 2.

Но была ли польза от Swift? Безусловно, что касается высокоуровневых задач, то Swift справляется с этим прекрасно. Писать код намного приятней, модерновый синтаксис не требующий постоянных точек с запятыми, очень много интуитивно понятного и полезного синтаксического сахара. Так что, несмотря на то, что использование Swift породило некоторые проблемы, в целом язык показался довольно приятным.

Проблема чувствительности микрофона

Итак, переписав часть кода на C, казалось что момент когда я смогу настроить свою гитару уже вот-вот наступит. Но тут возникла ещё одна неприятность о которой я совершенно не думал. Микрофон на iPhone ужасно обрезал низкочастотную часть спектра. Конечно, я предполагал что микрофоны в смартфонах отнюдь не идеальны, но всё оказалось намного хуже т.к. завал начинался уже на 200 Гц.



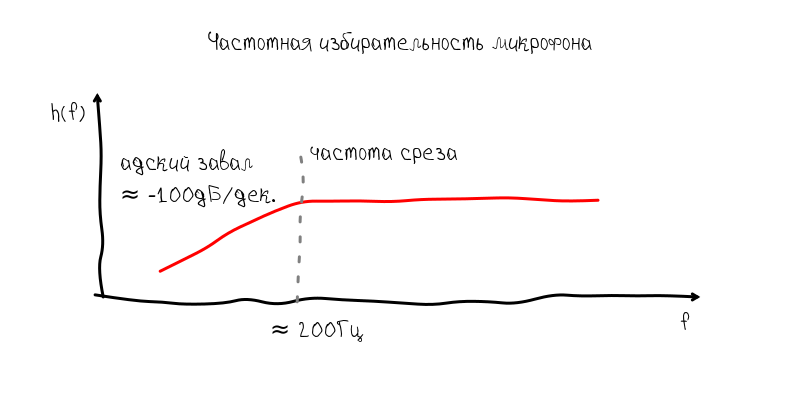
Что касается настройки гитары, то такой завал АЧХ делает невозможным настройку шестой струны, т.к. она имеет частоту примерно 80 Гц. При таком ослаблении основной тон начинает тонуть в гармониках с частотой 160 Гц, 240 Гц и т.д.



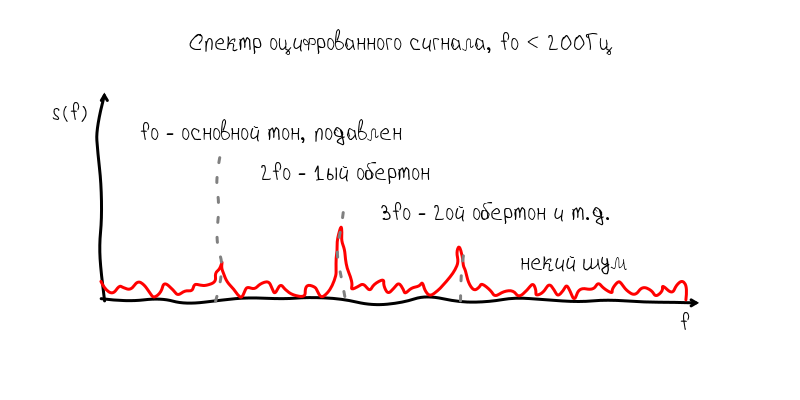
Я сразу наметил два возможных пути решения этой проблемы:

• если у основной частоты появляется близнец с частотой 0,5, то это должно свидетельствовать о том что основной тон заглушен и результирующая частота должна быть скорректирована и составлять 1/2f
• дать возможность пользователю подавлять обертоны низкочастотным фильтром, который будет отсекать частоты несколько большие чем тон струны

Первый вариант показался интереснее, т.к. не требовал от пользователя дополнительных усилий. Тем не менее, он оказался не совсем состоятельным, т.к. приводил ко многим плохим ситуациям. Например, основная частота порой резалась микрофоном настолько сильно, что была на уровне 1-2% от своей первой гармоники. Кроме того, т.к. резонатор гитары является очень нелинейным устройством, то частенько возникала ситуация когда вторая и третья, и даже четвёртая гармоника начинали конкурировать между собой по амплитуде. Это приводило к тому что захватывался тон в четыре раза выше чем основной.

В принципе, это проблемы можно было решить программным путём. Главное же разочарование было вызвано тем, что гармоники в гитаре очень сильно гуляют, поэтому настройка по ним никак не обеспечит точность в ±0,1 Гц. Связано это видимо тем, что основной тон задаётся струной с довольно стабильной частотой, наоборот же гармоники поддерживаются в основном за счёт колебаний в корпусе гитары и могут отклоняться на несколько Герц за время звучания струны.

Поэтому от первого решения пришлось отказаться в угоду более предсказуемого и менее удобного. Итак, низкочастотный фильтр имеет примерно такую частотную характеристику:



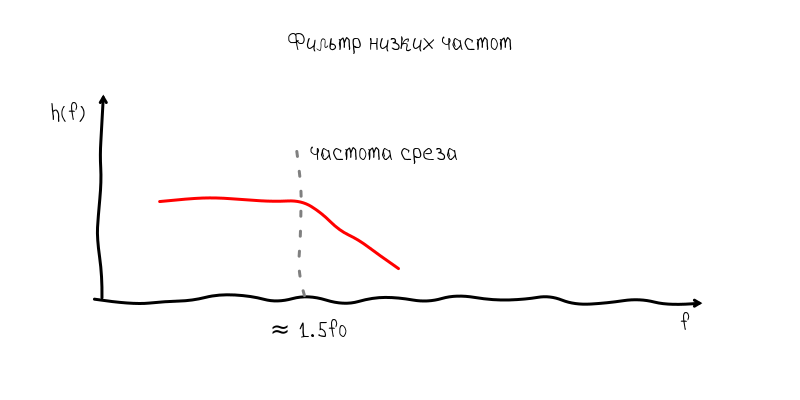
Завал справа от частоты среза обеспечивает подавление обертонов, так что основной тон снова становится превалирующим. Расплата за это общее снижение отношения сигнал–шум и как следствие небольшое снижение точности, однако в пределах допустимого.

Точность vs быстродействие

В цифровой обработке сигналов всегда всплывает задача выбора размера окна наблюдения. Большое окно наблюдения позволяет собирать больше информации, делать точную и стабильную оценку параметров сигнала. С другой стороны, это создаёт ряд проблем из-за того что требуется хранить и обрабатывать за раз большее количество отсчётов, плюс приводит к возникновению пропорциональной задержке в обработке сигнала.

В свою очередь Accelerate позволяет вычислять спектр последовательностей не превышающих 32768 отсчётов. Но такое количество отсчётов означает что шаг частотной сетки в спектре приблизительно равен 1,35 Гц. С одной стороны это допустимая величина, когда речь идёт о например ми первой октавы с частотой 440 Гц, т.е. ноты которая получается на открытой первой струне (самой тонкой). Но на шестой струне такая ошибка фатальна, т.к. между ми большой октавы и, например, ре большой октавы всего-то 3 Hz. Т.е. ошибка в 1,35 Гц это ошибка в полтона.



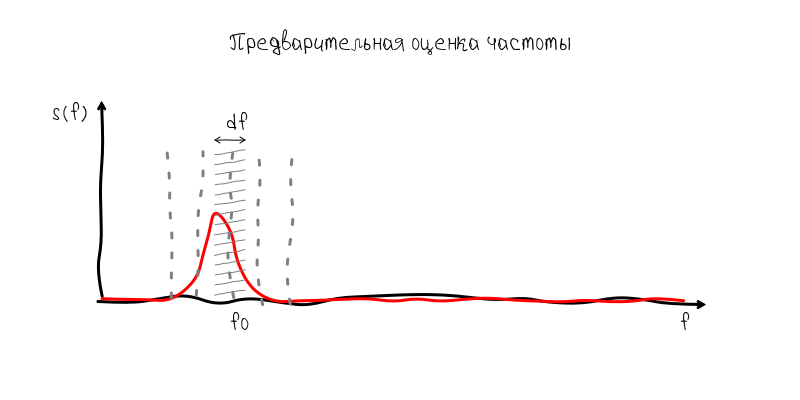
Тем не менее, решение этой проблемы довольно простое, но оно и демонстрирует всю силу частотно–временного анализа. Т.к. нет возможности накапливать несколько секунд сигнала, то мы можем накапливать значение спектра на частоте основного тона с повторным преобразованием Фурье. Математически результат будет эквивалентен обработки 1,35 Гц фильтром на частоте основного тона. Имея всего 16 комплексных отсчётов, мы можем повысить точность результата в 16 раз, т.е. примерно до 0,08 Гц что немного точнее ±0,1 Гц.



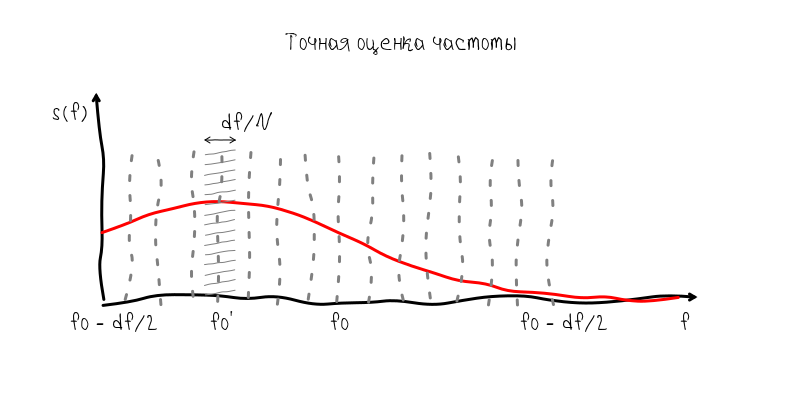
Другими словами, не имея информации о значении основного тона, нам пришлось бы для получения точности в ±0,1 Гц увеличить временное окно до 5 с и обрабатывать 163840 отсчётов. Но т.к. при временном окне в 0.743 с мы уже можем сделать оценку частоты с точность 1,35 Гц, то для более точной оценки достаточно накапливать отсчёты из крайне узкой полосы с дискретизацией в 2,7 Гц. Для этого вполне достаточно 2,7 Гц * 5 с = 13,75 комплексных отсчётов (или 16 если округлить и брать с запасом).

Сопоставление нот и частот

Это задача довольно легко решается на Swift. Я создал специальный класс Tuner в который занёс всю информацию о поддерживаемых инструментах и правилах сопоставления. Все эти расчёты основываются на двух формулах «baseFrequency * pow(2.0, (n — b) / 12.0)» и «12.0 * log(f / baseFrequency) / log(2) + b»,
где baseFrequency это частота базы 440 Гц или 256 Гц, b — номер ноты в целых числах, начиная от до субконтроктавы.

Код получился вполне китайским:

class Tuner {
    ...

    init(){
        addInstrument("guitar", [
            ("Standard", "e2 a2 d3 g3 b3 e4"),
            ("New Standard", "c2 g2 d3 a3 e4 g4"),
            ("Russian", "d2 g2 b2 d3 g3 b3 d4"),
            ("Drop D", "d2 a2 d3 g3 b3 e4"),
            ("Drop C", "c2 g2 c3 f3 a3 d4"),
            ("Drop G", "g2 d2 g3 c4 e4 a4"),
            ("Open D", "d2 a2 d3 f#3 a3 d4"),
            ("Open C", "c2 g2 c3 g3 c4 e4"),
            ("Open G", "g2 g3 d3 g3 b3 d4"),
            ("Lute", "e2 a2 d3 f#3 b3 e4"),
            ("Irish", "d2 a2 d3 g3 a3 d4")
        ])

        ...
    }

    ...

    func noteNumber(noteString: String) -> Int {
        var note = noteString.lowercaseString
        var number = 0
        var octave = 0

        if note.hasPrefix("c") { number = 0; }
        if note.hasPrefix("c#") { number = 1; }
        ...
        if note.hasPrefix("b") { number = 11; }

        if note.hasSuffix("0") { octave = 0; }
        if note.hasSuffix("1") { octave = 1; }
        ...
        if note.hasPrefix("8") { octave = 8; }

        return 12 * octave + number
    }

    func noteString(num: Double) -> String {
        var noteOctave: Int = Int(num / 12)
        var noteShift: Int = Int(num % 12)

        var result = ""
        switch noteShift {
            case 0: result += "c"
            case 1: result += "c#"
            ...
            default: result += ""
        }

        return result + String(noteOctave)
    }

    func noteFrequency(noteString: String) -> Double {
        var n = noteNumber(noteString)
        var b = noteNumber(baseNote)
        return baseFrequency * pow(2.0, Double(n - b) / 12.0);
    }

    func frequencyNumber(f: Double) -> Double {
        var b = noteNumber(baseNote);
        return 12.0 * log(f / baseFrequency) / log(2) + Double(b);
    }

    func frequencyDistanceNumber(f0: Double, _ f1: Double) -> Double {
        var n0 = frequencyNumber(f0)
        var n1 = frequencyNumber(f1)
        return n1 - n0;
    }

    func targetFrequency() -> Double {
        return noteFrequency(string) * fretScale()
    }

    func actualFrequency() -> Double {
        return frequency * fretScale()
    }

    func frequencyDeviation() -> Double {
        return 100.0 * frequencyDistanceNumber(noteFrequency(string), frequency)
    }
}

Визуализация стоячей волны

Что касается стоячей волны которая позволяет увидеть форму звуковой волны инструмента, то, как я уже писал, алгоритм абсолютно тривиален — по найденной основной частоте высчитывается длина волны и производится оценка фазы, а затем уже по найденному значению производится сдвиг. Данные берутся из вспомогательного буфера preview, который, в отличие от основного, не производит накопления. Т.е. работает по алгоритму «прыгающего окна» (англ. tumbling window):

    double waveLength = p->fd / f;
    size_t index = p->previewLength - waveLength * 2;
    double* src = &p->preview[index];

    // в цикле происходит разложение основного тона на реальную и мнимую составляющую
    double re = 0; double im = 0;
    for (size_t i = 0; i < waveLength*2; i++) {
        double t = (double)2.0 * M_PI * i / waveLength;
        re += src[i] * cos(t);
        im += src[i] * sin(t);
    }

    double phase = get_phase(re, im); // фаза волны относительно начала
    double shift = waveLength * phase / (2.0 * M_PI); // искомый сдвиг

    // положение начала стоячей волны
    double* shiftedSrc = &p->preview[index - (size_t)(waveLength - shift) - (size_t)waveLength];

Внешний вид

Внешний вид и навигацию я сделал на основе встроенного плеер, только вместо переключения по трекам происходит переключение по струнам:

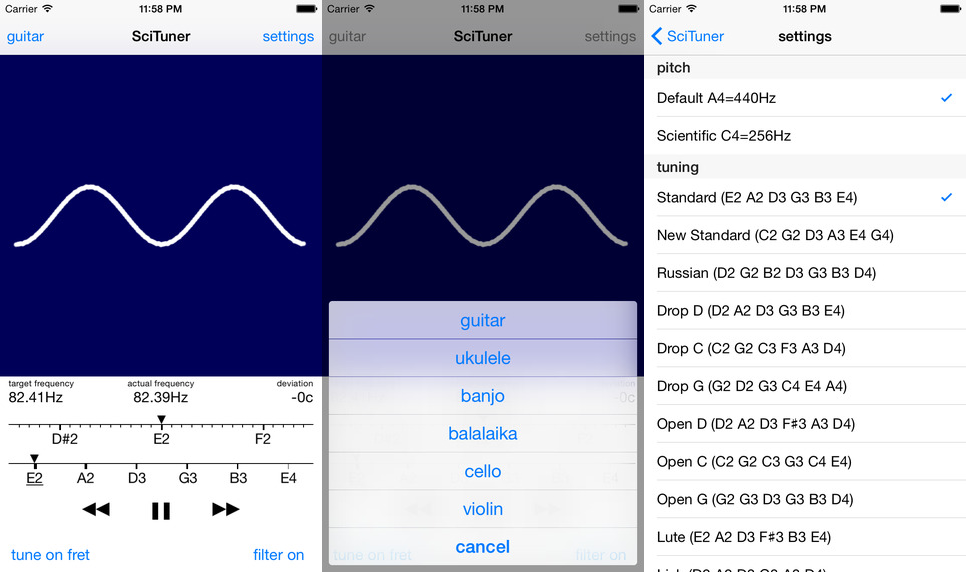
Заключение

Весь путь разработки приложения на Swift/C занял около двух месяцев. Приложение оказалось довольно сложным в реализации. Во-первых, производительность смартфонов всё ещё оставляет желать лучшего и решения «в лоб» на высокоуровневом языке оказываются абсолютно непригодными для бытового применения пользователями. Во-вторых, тема обработки звука ужасно непопулярная у разработчиков под iOs, поэтому информацию приходится собирать по крупицам. Хотя это касается, наверное, любой темы не связанной с UI при разработке под мобильные приложения. В-третьих, хоть Swift и неплохо связывается с C-данным, но всё-равно такой способ разработки ужасно неудобен и ужасно трудозатратен.

Несмотря на то, что статья получилась довольно весомой, многие тонкости и нюансы остались неосвещенными. Надеюсь исходный код приложения поможет прояснить непонятные моменты:

github.com/kreshikhin/scituner

Исходный код сопровождён MIT-лицензией. Поэтому можете смело использовать интересующие вас участки кода или весь код проекта в своих целях.