
Введение
Еще в 1964 году известный специалист Дональд Кнут предложил простой тест [1], названный им «Man or boy?» (в вольном переводе «взрослый или детский?») для проверки трансляторов с языка Алгол-60.
Тест выглядел так:
begin
real procedure A(k,x1,x2,x3,x4,x5); value k; integer k;
begin
real procedure B; begin k:=k-1; B:=A:=A(k,B,x1,x2,x3,x4); end B;
if k<=0 then A:=x4+x5 else B;
end A;
outreal(A(10,1,-1,-1,1,0);
end;Смысл теста в построении в памяти дерева из рекурсивных вызовов процедур A и B, причем каждый вызов должен вычисляться в нужном контексте, иначе конечный результат (в оригинальном примере -67 для начального числа, равного 10) недостижим. Начальное число N при запуске теста определяет максимальную глубину дерева вызовов как 2(N-1).
Тест оказался удачным как для демонстрации возможностей языковых средств, так и для оценки ресурсов, предоставляемых операционными системами, поэтому он переведен на разные языки [2], а допустимое начальное число на больших системах намного превысило первоначальное значение 10.
Часть первая, 32-х разрядная. Рекорд почти не виден.
Автор статьи также решил проверить используемую им систему на PL/1, скопировав соответствующий пример на этом языке из [2]. Утверждалось, что пример корректно работал в трех разных средах: OS PL/I V2.3.0, Enterprise PL/I V3R9M0 и PL/I for Windows V8.0, при этом допустимое начальное число достигало значений 15, 23 и 26 соответственно.
Однако для испытуемого компилятора PL/1-KT [3] ничего не вышло, поскольку при передаче параметра-ссылки на процедуру он автоматически не передавал соответствующий контекст, т.е. по терминологии Кнута представлял собой «детскую» систему.
Это фиаско заставило проанализировать задачу в целом и попытаться «спасти лицо» следующим образом:
а) решить задачу средствами языка не подражая «алгольной» записи. Имевшийся пример не сработал, но в стандарте PL/1 и не оговорено, что передача ссылки на процедуру должна вызывать передачу или запоминание ее контекста, хотя очевидно, что приведенные выше компиляторы сделали это. В случае если не удастся превзойти результаты, полученные этими «взрослыми» компиляторами, их действительно придется признать «умными». Однако если все-таки удастся получить лучший результат, значит, они не оптимально использовали ресурсы и ценность их «ума» становится неочевидной.
б) полностью мобилизовать все ресурсы операционной системы на решение данной задачи. Во-первых, это необходимое условие получения наилучшего результата, а во-вторых, и это главное, примененные методы мобилизации ресурсов (памяти) в дальнейшем можно будет использовать в реальных задачах.
Были приняты также следующие ограничения:
1. Тест должен выполняться на «заурядном», доступном компьютере с обычной операционной системой. Конкретно был взят ультраноутбук SONY с процессором Intel Solo 1,33 ГГц и 1 Гб ОЗУ. Операционная система Windows Vista Business. Хотя время выполнения данного теста не считается определяющим, оно должно было быть приемлемым.
2. Тест должен иметь нормальный ввод и вывод и выполняться в реальной рабочей, а не искусственной среде. Например, практически все программы не могут обойтись без загрузки стандартных библиотек вроде kernel32.dll, хотя в данном случае (ответ - единственное значение) можно было бы обойтись даже без стандартного вывода.
Алгоритмически тест должен быть решен исключительно стандартными средствами языка. Очевидно, что заведомо наилучшие результаты дал бы ассемблер, но тогда теряется весь смысл теста как проверки языка.
Наоборот, задача мобилизации ресурсов должна решаться не языковыми средствами, а модернизацией системной библиотеки и настройкой операционной среды, поскольку в самом языке (в данном случае в PL/1) допустимый размер ресурсов не определен.
Решение теста Кнута
Общая идея новой реализации теста Кнута на PL/1 такова:
1. Моделируется стековая память как массив структур. Индексом такого массива является вложенность процедуры А. При очередном вызове А вложенность увеличивается, при выходе из А – уменьшается.
2. Вложенность полностью определяет текущий контекст вызова А и В и задается как параметр процедуры B.
3 Вложенность каждого вызова добавляется также к параметрам процедуры А как явное указание контекста вызовов, т.е. вместо 6 у нее становится 11 параметров.
Такой подход позволяет отказаться от формального объявления в программе процедур А и В рекурсивными, хотя фактически они продолжают оставаться таковыми. При этом выключается «умное» запоминание рекурсивных данных средствами компилятора и остается только явно заданное программистом. Собственно стек требуется теперь лишь для хранения адресов возврата из процедур А и В.
На одну пару вызовов А и В потребуется 4+4 байт адресов возврата, 4 байта для текущего значения начального числа, 4х4 байт для вызовов-параметров и 4х4 байт для их контекстов (пятый вызов и его контекст как будет показано ниже не требует запоминания). Итого получается 44 байта. Тогда для выполнения теста с "рекордным" начальным числом 27 потребуется глубина в 226 пар вызовов или 2,952,790,016 байт. Учитывая, что 32-х разрядная Windows позволяет выделять программам до 3 Гбайт виртуальной памяти, расчет с начальным числом 27 становится принципиально возможным.
Выделение памяти для теста Кнута
При задании ключа /3GB в файле BOOT.INI Windows XP, или при выполнении команды bcdedit /set increaseuserva 3221225471 для 32-х разрядной Windows Vista и Windows-7, операционная система выделяет программе до 3 Гбайт виртуальной памяти, при условии, что в заголовке EXE-файла установлен ключ IMAGE_FILE_LARGE_ADDRESS_AWARE.
Однако возникает проблема непрерывного пространства, поскольку обычно системные библиотеки типа kernel32.dll или user32.dll продолжают загружаться в конец второго, а не третьего гигабайта, разбивая свободную память на две неравные области. В данном случае, дело облегчалось тем, что для теста область стека можно задавать отдельно от области, выделяемой для массива структур.
Первая задача, которую нужно было решить – это сделать доступной программе на PL/1 (т.е. операторам ALLOCATE и FREE) области памяти и «ниже» и «выше» системных библиотек. Поскольку «куча» в данной реализации PL/1 представляет собой двунаправленный связанный список фрагментов памяти с отметкой занятых и свободных, данная задача решилась легко: области, занятые системными библиотеками, просто помечались как занятые до конца работы программы, для чего в конце доступных областей создавались дополнительные фиктивные ссылки на занятые области.
Некоторую проблему составило и то, что автор сразу не догадался, как определить наибольший размер непрерывной свободной области, который можно указать при выделении памяти с помощью процедуры Win-32 API VirtualAlloc. Поэтому просто задавался максимально возможный размер памяти при обращении к VirtualAlloc. Если запрос не получался, размер уменьшался на 50% от предыдущей попытки, если получался – захваченная область тут же освобождалась обращением к VirtualFree, и размер увеличивался на 50% от предыдущей попытки. Такими итерациями быстро находятся все свободные области с заданной точностью (конкретно задана точность в 1 Мбайт). Затем все найденные области сортируются в порядке возрастания адресов, и из них составляется связанный список свободных с автоматическим созданием фиктивных смежных занятых областей, «обходящих» адресное пространство системных библиотек.
Все эти действия были вставлены внутрь системной библиотеки PL/1 и теперь автоматически выполняются при каждом запуске любой PL/1-программы. В результате доступная для использования «куча» в программах возросла почти до 3200 Мбайт.
Однако наличие двух даже больших несмежных областей памяти все равно не позволяло выделить область для массива из 226 элементов по 36 байт каждый, т.е. размером 2416 Мбайт, поскольку размер одной области стал около 2140 Мбайт, а второй – 1073 Мбайт. Поэтому операторами ALLOCATE приходится выделять память для теста по частям:
1. Сначала оператором ALLOCATE выделяется необходимая область для стека размером 8х226 байт плюс некоторый резерв для служебных целей. Поскольку в PL/1-KT возможно прямое обращение к регистрам [3], адрес вершины выделенной области прямо присваивается регистру стека ESP.
2. С помощью имеющейся в PL/1-KT служебной процедуры определения максимального размера непрерывной свободной области MAXWDS находится и затем оператором ALLOCATE захватывается оставшийся наибольший непрерывный фрагмент свободной памяти. Очевидно, что это опять будет фрагмент из первой области, так как после выделения стека в ней еще останется почти 1.5 Гбайт.
3. Опять с помощью процедуры MAXWDS находится и затем захватывается самая большая из оставшихся свободными областей. Очевидно, что в данном случае это будет вся область в «третьем» гигабайте.
В результате из «кучи» выделена гарантированно непрерывная область для стека и две не смежные области для массива (адреса первой области «ниже» адресов второй), сумма которых достаточна для выполнения теста с начальным числом 27.
Далее используется допустимость описания в PL/1 «базированных» массивов, поскольку в качестве «базы» можно задавать не только указатель, но и процедуру без параметров, возвращающую указатель. В этом случае компилятор будет автоматически генерировать вызов такой процедуры при каждом обращении к массиву. Сама процедура-указатель написана так, как показано на рис. 1: если текущий индекс массива X1 «входит» в первую выделенную область памяти, процедура-указатель возвращает указатель P1 на первую область, а компилятор генерирует смещение A1. Если же индекс X2 массива превышает размер первой области, процедура-указатель вернет фиктивный указатель P3, равный указателю на вторую область P2 минус размер первой области. В точке обращения компилятор генерирует смещение массива A2 и прибавит его к фиктивному указателю P3, получив тем самым доступ к нужному элементу.
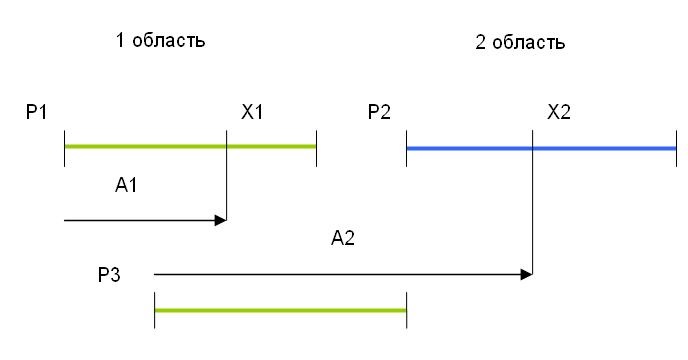
Такой прием позволяет не загромождать текст программы вычислениями указателей, хотя из-за рекурсии несколько дополнительных присваиваний все же появляются. Принципиально возможно размещать массив и в большем числе несмежных областей, но в данном случае двух уже достаточно.
Исходный текст реализации теста Кнута на языке PL/1-KT
Исходный текст приведен ниже. Он должен лишь убедить читателей, что никакого обмана в проведении вычислений нет, действительно создается дерево вызовов. В программе присутствует ряд несущественных деталей, позволяющих контролировать ход вычислений. Замысловатые действия при вычислении суммы X4+X5 связаны с экономией памяти. Ссылка на X5 нужна лишь один раз, но перед этим необходимо вычислить X4 (если сначала вычислять X5, а затем X4, изменится число шагов теста). Поэтому ссылка на X5 запоминается на месте X4, а контекст X5 на месте контекста X4. Потом на этом же месте контекста запоминается результат вычисления X4, а находившийся там ранее контекст с помощью оператора обмена перемещается в переменную Z. Все это позволяет не выделять память или стек для хранения промежуточного результата сложения X4 и X5, а также память для хранения однократно требующейся ссылки на X5 и ее контекста. Иначе пришлось бы увеличивать размер элемента массива еще на 12 байт.
-----------------------------------------------------------------------------
// РКК "'ЭНЕРГИЯ" ТЕСТ НА ВОЗМОЖНОСТИ СИСТЕМЫ "ВЗРОСЛЫЙ ИЛИ ДЕТСКИЙ"
// ОТДЕЛ ??? СЕКТОР ??? ИCПOЛHИTEЛЬ: КАРАВАЕВ ЯЗЫK PL/1-KT
-----------------------------------------------------------------------------
// MOДУЛЬ MORB BEPCИЯ 1.0 ДATA COЗДAHИЯ 13.5.2012
// ИCПOЛЬЗУEMЫE MATEPИAЛЫ: HTTP://EN.WIKIPEDIA.ORG/WIKI/MAN_OR_BOY_TEST
-----------------------------------------------------------------------------
// ВНЕСЕННЫЕ ИЗМЕНЕНИЯ:
-----------------------------------------------------------------------------
// МОДУЛЬ ВЫПОЛНЯЕТ ТЕСТ ДОНАЛЬДА КНУТА
// ДЛЯ ДОСТИЖЕНИЯ БАЗЫ=27 НЕОБХОДИМО ЗАПУСКАТЬ WINDOWS-XP C КЛЮЧОМ /3GB
// ВНУТРИ BOOT.INI ИЛИ С КОМАНДОЙ BCDEDIT /SET INCREASEUSERVA=3221225471 ДЛЯ
// WINDOWS-VISTA ИЛИ WINDOWS-7
----------------------------------------------------------------------------
MORB: PROC(БАЗА) MAIN;
DECLARE
//---- НАЧАЛЬНОЕ ЧИСЛО ТЕСТА ИЗ КОМАНДНОЙ СТРОКИ (ПО УМОЛЧАНИЮ НОЛЬ) ----
БАЗА CHAR(*) VAR,
//---- ЗАДАВАЕМЫЕ РЕСУРСЫ В PL/1-KT ----
?MEMORY FIXED(31) EXT INIT(-1), // ИСПОЛЬЗУЕМ ВСЮ ПАМЯТЬ
?MEM_ALL FIXED (7) EXT INIT(1), // НЕ СМЕЖНЫМИ УЧАСТКАМИ
//---- СЛУЖЕБНЫЕ ПРОЦЕДУРЫ PL/1-KT ----
MAXWDS RETURNS(FIXED(31)), // ПОДСЧЕТ МАКСИМАЛЬНОГО УЧАСТКА
//---- ТАБЛИЦА СОБСТВЕННЫХ ЗНАЧЕНИЙ И КОНТЕКСТОВ ----
1 ТАБЛИЦА (1:2) BASED(АДР_ТАБЛ()), // РАЗМЕРНОСТЬ 1:2 ФИКТИВНА
2 KK FIXED(31), // ТЕКУЩЕЕ ЗНАЧЕНИЕ НАЧАЛЬНОГО ЧИСЛА
2 (XX1, // ВЫЗОВЫ
XX2,
XX3,
XX4) ENTRY(FIXED(31)) RETURNS(FIXED(31)),
2 (NN1,
NN2, // КОНТЕКСТЫ
NN3,
NN4) FIXED(31),
//---- ПАМЯТЬ, ВЫДЕЛЕННАЯ 1 УЧАСТКУ ----
P1 PTR, // УКАЗАТЕЛЬ НА 1 УЧАСТОК
ДЛН1 FIXED(31), // ДЛИНА 1 УЧАСТКА В СТРОКАХ ТАБЛИЦЫ
//---- ПАМЯТЬ, ВЫДЕЛЕННАЯ 2 УЧАСТКУ ----
P2 PTR, // УКАЗАТЕЛЬ НА 2 УЧАСТОК
F2 FIXED(31) DEF(P2), // ОН ЖЕ КАК ЦЕЛОЕ ДЛЯ АДРЕСНОЙ АРИФМЕТИКИ
ДЛН2 FIXED(31), // ДЛИНА 2 УЧАСТКА В СТРОКАХ ТАБЛИЦЫ
P2_ФИКТ PTR, // ФИКТИВНЫЙ АДРЕС НАЧАЛА 2 УЧАСТКА
F2_ФИКТ FIXED(31) DEF(P2_ФИКТ), // ОН ЖЕ КАК ЦЕЛОЕ
ДЛН FIXED(31), // ОБЩЕЕ ЧИСЛО СТРОК ТАБЛИЦЫ ДЛЯ КОНТРОЛЯ
//---- ВЛОЖЕННОСТЬ ВЫЗОВОВ ПРОЦЕДУРЫ A ----
N FIXED(31), // ТЕКУЩАЯ ВЛОЖЕННОСТЬ
ИНДЕКС FIXED(31), // ВЛОЖЕННОСТЬ КАК ИНДЕКС ТАБЛИЦЫ
//---- УКАЗАТЕЛЬ НА ОБЛАСТЬ СТЕКА ----
P4 PTR, // УКАЗАТЕЛЬ НА НАЧАЛО ОБЛАСТИ СТЕКА
F4 FIXED(31) DEF(P4), // ОН ЖЕ КАК ЦЕЛОЕ ДЛЯ АДРЕСНОЙ АРИФМЕТИКИ
?ESP FIXED(31), // ДЛЯ ПРЯМОГО ДОСТУПА К ESP В PL/1-KT
РАЗМ_СТЕК FIXED(31), // РАЗМЕР СТЕКА
//---- РАБОЧИЕ ПЕРЕМЕННЫЕ И СЧЕТЧИКИ ----
I FIXED(31), // НАЧАЛЬНОЕ ЧИСЛО ЗАПУСКА ТЕСТА
L FIXED(31), // КОНЕЧНЫЙ ОТВЕТ ТЕСТА
Z FIXED(31), // ОТВЕТ ПРОЦЕДУРЫ A
J FIXED(31); // СЧЕТЧИК ДЛЯ ВЫДАЧИ НА ДИСПЛЕЙ
-----------------------------------------------------------------------------
//---- ВЫДАЧА ШАПКИ ----
PUT SKIP(2) LIST('^I^IТЕСТ "MAN OR BOY", ВЕРСИЯ',?DATE);
//---- ВВОД НАЧАЛЬНОЙ БАЗЫ ИЗ КОМАНДНОЙ СТРОКИ ----
IF LENGTH(БАЗА)>0 THEN I=БАЗА;
//----------------- ВЫДЕЛЕНИЕ РЕСУРСОВ ДЛЯ РАБОТЫ ТЕСТА ---------------------
PUT SKIP(2) EDIT(TOTWDS,' ДОСТУПНЫХ СЛОВ ПАМЯТИ, ВЫДЕЛЕНО:')
(P'ZZZ,999,999,999',A);
PUT SKIP;
//---- ВЫДЕЛЯЕМ МАКСИМАЛЬНУЮ ПАМЯТЬ ДЛЯ СТЕКА ----
РАЗМ_СТЕК=2**26*8+1024*1024; // ДЛЯ БАЗЫ 27
ALLOCATE(РАЗМ_СТЕК) SET(P4); // ВЫДЕЛЯЕМ МЕСТО ДЛЯ СТЕКА
?ESP=F4+РАЗМ_СТЕК; // ВЕРШИНУ - ПРЯМО В РЕГИСТР ESP
//---- ВЫДЕЛЯЕМ ПАМЯТЬ (1 УЧАСТОК) ДЛЯ ТАБЛИЦЫ КОНТЕКСТОВ ----
ДЛН1=MAXWDS*2; // БЕРЕМ МАКСИМАЛЬНЫЙ НЕПРЕРЫВНЫЙ УЧАСТОК
ALLOCATE(ДЛН1) SET (P1); // ВЫДЕЛЯЕМ ЕГО КАК 1 УЧАСТОК
ДЛН1=ДЛН1/36; // ПЕРЕВЕЛИ В ЧИСЛО СТРОК 1 УЧАСТКА
PUT SKIP EDIT(ДЛН1,' СТРОК ТАБЛИЦЫ 1 УЧАСТКА')(P'ZZZ,ZZZ,999,999',A);
//---- ВЫДЕЛЯЕМ ПАМЯТЬ (2 УЧАСТОК) ДЛЯ ТАБЛИЦЫ КОНТЕКСТОВ ----
ДЛН2=MAXWDS*2; // БЕРЕМ МАКСИМАЛЬНЫЙ НЕПРЕРЫВНЫЙ УЧАСТОК
ALLOCATE(ДЛН2) SET(P2); // ВЫДЕЛЯЕМ ЕГО КАК 2 УЧАСТОК
ДЛН2=ДЛН2/36; // ПЕРЕВЕЛИ В ЧИСЛО СТРОК 2 УЧАСТКА
PUT SKIP EDIT(ДЛН2,' СТРОК ТАБЛИЦЫ 2 УЧАСТКА')(P'ZZZ,ZZZ,999,999',A);
//---- ПОЛУЧАЕМ ЗНАЧЕНИЯ ДЛЯ УСКОРЕНИЯ ВЫЧИСЛЕНИЙ ----
ДЛН=ДЛН1+ДЛН2; // ОБЩЕЕ ЧИСЛО СТРОК ДЛЯ КОНТРОЛЯ ИНДЕКСА
F2_ФИКТ=F2-ДЛН1*36; // ФИКТИВНОЕ НАЧАЛО 2 УЧАСТКА
PUT SKIP(2) LIST('-'(40),'^M');
//------------------------- ЦИКЛ ЗАПУСКОВ ТЕСТА ----------------------------
DO I=I TO 27; // ОТ ЗАДАННОГО ЧИСЛА ИЛИ НУЛЯ ДО МАКСИМАЛЬНОГО
//---- ВЫДАЛИ ЗАГОЛОВОК ----
PUT SKIP EDIT(TIME,' ЗАПУСК С НАЧАЛЬНЫМ ЧИСЛОМ =',I)(A,A,F(2));
PUT SKIP;
//---- СОБСТВЕННО РАСЧЕТ (ВНУТРИ ЕСТЬ ВЫДАЧА НА ДИСПЛЕЙ) ----
L=A((I), X1,0, X2,0, X3,0, X4,0, X5,0);
//---- ВЫДАЧА ОТВЕТА ----
PUT LIST(' '(20),'^M');
PUT SKIP EDIT(TIME,'БАЗА = ', I,L)(A(8),X(1),A,P'z9b',P'---,---,---,--9');
PUT SKIP LIST('-'(40),'^M');
END I;
//------------------- ПЕРВАЯ РЕКУРСИВНАЯ ПРОЦЕДУРА ТЕСТА --------------------
A:PROC(K,X1,N1,X2,N2,X3,N3,X4,N4,X5,N5) RETURNS(FIXED(31));
DECLARE
K FIXED(31), // БАЗОВОЕ ЧИСЛО
(X1,X2,X3,X4,X5) ENTRY(FIXED(31)) RETURNS(FIXED(31)), // ВЫЗОВЫ
(N1,N2,N3,N4,N5) FIXED(31); // НОМЕР КОНТЕКСТА ВЫЗОВОВ
//---- УВЕЛИЧИВАЕМ ВЛОЖЕННОСТЬ ПРОЦЕДУРЫ A ----
N+=1;
//---- ПРОВЕРКА ПЕРЕПОЛНЕНИЯ ТАБЛИЦЫ СОБСТВЕННЫХ ЗНАЧЕНИЙ ----
IF N>ДЛН THEN PUT SKIP LIST('ТАБЛИЦА',STOP);
//---- ВЫВОДИМ ТЕКУЩЕЕ СОСТОЯНИЕ ТЕСТА НА ДИСПЛЕЙ ----
J+=1;
IF J>8191 THEN // НЕ НА КАЖДОМ ЦИКЛЕ ДЛЯ СКОРОСТИ
{;
J=0;
PUT EDIT(TIME,' ',N,'^M')(A,A,P'ZZZ,999,999',A);
};
//-------------------- САМО ВЫПОЛНЕНИЕ РЕКУРСИВНОГО ТЕСТА -------------------
//---- СОХРАНЯЕМ ОЧЕРЕДНЫЕ СОБСТВЕННЫЕ ЗНАЧЕНИЯ ПРОЦЕДУРЫ A ----
ИНДЕКС=N; // ДЛЯ ВЫДАЧИ АДРЕСА 1/2 УЧАСТКА
XX1(N)=X1; // ЗАПОМИНАЕМ ВЫЗОВЫ
XX2(N)=X2;
XX3(N)=X3;
XX4(N)=X4;
NN1(N)=N1; // ЗАПОМИНАЕМ КОНТЕКСТЫ ВЫЗОВОВ
NN2(N)=N2;
NN3(N)=N3;
NN4(N)=N4;
KK (N)=K; // ЗАПОМИНАЕМ ТЕКУЩЕЕ БАЗОВОЕ ЧИСЛО
IF K<=0 THEN // ИЩЕМ СУММУ ВЫЗОВОВ X4 И X5
{;
XX4(N)=X5; // \ ЗАПОМНИЛИ ВЫЗОВ
NN4(N)=N5; // / И КОНТЕКСТ #5
Z=X4(N4); // ВЫПОЛНИЛИ ВЫЗОВ #4 В КОНТЕКСТЕ #4
ИНДЕКС=N; // ДЛЯ ВЫДАЧИ АДРЕСА 1/2 УЧАСТКА
NN4(N)<=>Z; // ЗАПОМНИЛИ РЕЗУЛЬТАТ #4 И ДОСТАЛИ КОНТЕКСТ #5
Z=XX4(N)(Z); // ВЫПОЛНИЛИ ВЫЗОВ #5 В КОНТЕКСТЕ #5
ИНДЕКС=N; // ДЛЯ ВЫДАЧИ АДРЕСА 1/2 УЧАСТКА
Z+=NN4(N); // ЗНАЧЕНИЕ X4+X5
};
ELSE Z=B((N)); // ИНАЧЕ РЕКУРСИВНО ОБРАЩАЕМСЯ К ПРОЦЕДУРЕ B
//---- УМЕНЬШАЕМ ВЛОЖЕННОСТЬ A ----
N-=1;
//---- ВЫХОДИМ С ОТВЕТОМ ----
RETURN(Z);
//-------------------- ВТОРАЯ РЕКУРСИВНАЯ ПРОЦЕДУРА ТЕСТА -------------------
B:PROC(Y) RETURNS(FIXED(31));
DCL Y FIXED(31); // ТЕКУЩИЙ КОНТЕКСТ ВЫЗОВА
ИНДЕКС=Y; // ДЛЯ ВЫДАЧИ АДРЕСА 1/2 УЧАСТКА
KK(Y)-=1; // УМЕНЬШАЕМ БАЗОВОЕ ЧИСЛО НУЖНОГО СОСТОЯНИЯ
//---- РЕКУРСИВНО ВЫЗЫВАЕМ ПЕРВУЮ ПРОЦЕДУРУ ----
RETURN(A(KK(Y),B,Y,XX1(Y),NN1(Y),XX2(Y),NN2(Y),XX3(Y),NN3(Y),XX4(Y),NN4(Y)));
END B;
END A;
//------------ ПРОЦЕДУРА ВЫДАЧИ АДРЕСА 1 ИЛИ 2 УЧАСТКА ТАБЛИЦЫ --------------
АДР_ТАБЛ:PROC RETURNS(PTR);
//---- ЕСЛИ ИНДЕКС ВНУТРИ 1 УЧАСТКА ПАМЯТИ ----
IF ИНДЕКС<=ДЛН1 THEN RETURN(P1); // ВОЗВРАЩАЕМ ССЫЛКУ НА 1 УЧАСТОК
//---- ЕСЛИ ИНДЕКС ВНУТРИ 2 УЧАСТКА ПАМЯТИ ----
RETURN(P2_ФИКТ); // ВОЗВРАЩАЕМ ФИКТИВНОЕ НАЧАЛО 2 УЧАСТКА
END АДР_ТАБЛ;
//---------------------- ВЫЗОВЫ НАЧАЛЬНЫХ ЗНАЧЕНИЙ --------------------------
X1:PROC(Y) RETURNS(FIXED(31)); DCL Y FIXED(31); RETURN( 1); END X1;
X2:PROC(Y) RETURNS(FIXED(31)); DCL Y FIXED(31); RETURN(-1); END X2;
X3:PROC(Y) RETURNS(FIXED(31)); DCL Y FIXED(31); RETURN(-1); END X3;
X4:PROC(Y) RETURNS(FIXED(31)); DCL Y FIXED(31); RETURN( 1); END X4;
X5:PROC(Y) RETURNS(FIXED(31)); DCL Y FIXED(31); RETURN( 0); END X5;
END MORB;
Результаты работы теста
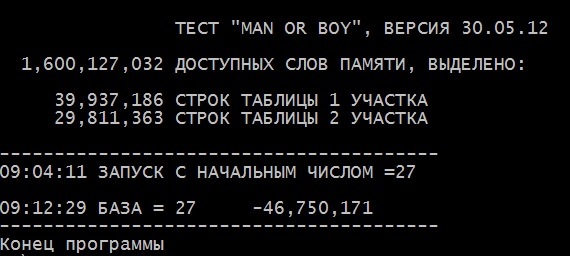
Результат приведен на рис. 2. Тест с начальным числом 27 выполнился менее, чем за 9 минут, получив значение -46750171 и построив для этого дерево глубиной 67 миллионов вложенных вызовов процедур А и В, а всего вызвав эти процедуры 292 миллиона раз. Поскольку компьютер имел лишь 1 Гбайт физической памяти, происходило обращение к диску, что существенно замедляло работу.
Заключение
Конечно, можно считать, что тест на «взрослость» все-таки в части рекурсии не выполнен, поскольку не удалось записать алгоритм в коротком алголоподобном стиле. Однако если обратиться к сути этой остроумной задачи (составление максимально возможного дерева в памяти и обход его), то окажется, что она выполнима на проверяемом компиляторе и даже с лучшими результатами, чем у «взрослых» компиляторов PL/1 (да, пожалуй, и всех других 32-х разрядных систем). Ведь ими был достигнут уровень 26 лишь на 64-х разрядной Windows-8 с 16 Гбайт оперативной памяти. Здесь же достигнут результат 27, уже близкий к теоретическому пределу для 32-х разрядных систем и при этом автор, занимаясь вроде бесполезной задачей, получил механизм использования памяти «выше» системных библиотек и метод обращения к единому массиву в несмежных областях памяти, пригодные уже не для искусственного теста, а для практического применения.
Часть вторая. 64-х разрядная. Опыты со стеком.
Описание теста Д. Кнута «Man or boy?» на сайте [2] мне попалось на глаза случайно, но очень увлекло. Помнится, в прекрасном произведении «Три толстяка» был один персонаж – (цирковой) стрелок. Он во время погони увидел пролетающий воздушный шарик и сразу обо всем забыл, в том числе о погоне. Главное для него стало – попасть в шар. Я стал в чем-то похож на этого стрелка (который, кстати, в шар так и не попал- помешала шляпа стоящего рядом директора). В ущерб работе и другим занятиям, главным для меня стало – выполнить тест Кнута с хорошим результатом, т.е. максимально эффективно использовать доступные стек и память так, чтобы добиться правильного завершения теста с наибольшим базовым значением. Базовое значение теста по существу является показателем степени числа рекурсивно вложенных вызовов, если такое число представить в виде 2n.
Дело осложнялось тем, что компилятор, который я использую [3], не запоминает контекст вызова рекурсивных процедур и, по сути, вообще не может выполнить этот тест. Эти трудности были обойдены моделированием запоминания контекстов через обращение к массиву, а собственно аппаратный стек стал использоваться только для запоминания адресов возврата из рекурсивных процедур. Кроме этого, возникли сложности с фрагментацией памяти из-за фиксированного размещения системных библиотек Windows-XP, что не позволяло использовать все доступные 3 Гбайт памяти как одну непрерывную область. Но и эти сложности были преодолены. Результаты я представил в статье (см. часть 1) и был очень горд тем, что смог выполнить на обычном и слабом ноутбуке тест с базовым значением 27, что на тот момент являлось «мировым рекордом» среди всех результатов, перечисленных на сайте [2].
Поскольку этот сайт постоянно обновляется и дополняется, я года полтора продолжал считать себя действующим чемпионом по выполнению теста Кнута, хотя и отдавал себе отчет в том, что, например, массовый переход на Win64 изменит эту ситуацию. И вот на сайте появилось сообщение, что тест, написанный на Haskell, выполнен для базового значения 30. Таким образом, по использованным ресурсам мой рекорд был превзойден сразу в восемь раз, а я превратился в «экс-чемпиона». Разумеется, новый рекорд был установлен не на маленьком домашнем ноутбуке c 32-разрядной Windows, а на солидном AMD Opteron 6282SE c 384 Гбайт доступной памяти в «куче».
Но и я к тому времени приобрел для дома ноутбук c Intel Core i5-3210M, c 4 Гбайт памяти и домашней Windows 7 и занялся переводом своих средств разработки на Win64. Естественно, что первым тестом, который проверялся для доработанного компилятора, стал все тот же тест Кнута. С точки зрения языка PL/1, на котором я пишу, все получилось изящно – в доработанном для Win64 компиляторе появилась возможность определять переменные как целые со знаком размером в 8 байт, т.е. с атрибутами BINARY FIXED(63), которыми и были заменены в исходном тексте теста (текст на PL/1 см. часть 1) все переменные, ранее имевшие тип BINARY FIXED(31). Кроме этого, появилось все-таки не два, а целых три несмежных участка памяти (из-за странной загрузки системных библиотек), а также вместо регистра ESP теперь необходимо использовать RSP. Ради интереса, я добавил и вывод максимальной глубины вложений.
В целом, сложности, которые пришлось преодолевать в Win32, остались и в Win64. Например, некоторые системные библиотеки вроде NTDLL.DLL или KERNEL32.DLL и в Windows 7 упорно не хотят загружаться в «верхние» адреса памяти, разбивая свободное адресное пространство на несколько несмежных фрагментов, хотя теперь «потери» при этом не превышают 1 Гбайт.
Однако самым сложным для меня оказалась работа с «большим» стеком. Даже психологически трудно после стольких лет работы с Win32 привыкнуть к тому, что для хранения указателя вершины стека реально нужно 8 байт. Помните старое заявление Билла Гейтса, что «640 Кбайт хватит для всех задач»? Так вот, для выполнения теста Кнута с базовым значением 30 даже при моем построении алгоритма (напомню, в стеке хранится только дерево из адресов возврата двух рекурсивных процедур) для стека уже требуется 16*229=4294967296 байт. И это только для хранения адресов возврата! Но возникшую сложность работы со стеком я решил обратить себе на пользу и специально в разных других тестах, там, где таких больших значений не требовалось, начал устанавливать значение указателя стека больше 232. Этот прием позволил быстро выявить все свои ошибки перевода с Win32 на Win64, связанные со стеком. И речь идет не просто о пропущенных в ассемблерных текстах системных подпрограмм ESP вместо требуемых теперь RSP, но и о более сложных связях. Тест Кнута неожиданно оказался прекрасной проверкой правильности средств разработки в среде Win64.
В результате мои программы стали более «ошибкоустойчивы» и как приятный бонус я вернул себе звание «чемпиона мира», выполнив в Windows 7 тест с базовым значением 31.
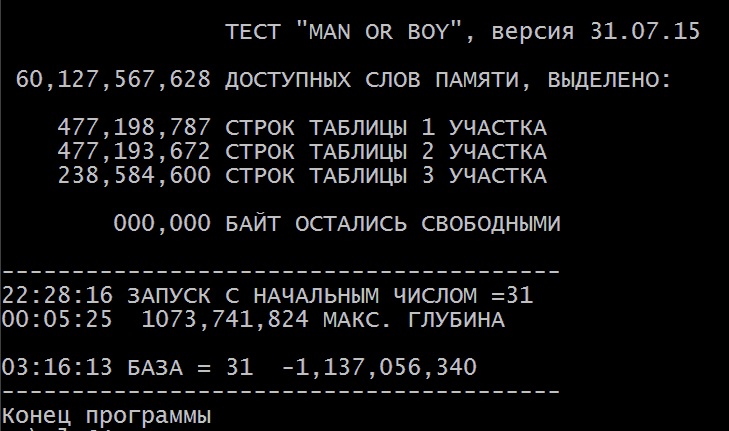
Как следует из этого «скриншота», через полтора часа после запуска теста глубина вложенных вызовов превысила миллиард. Т.е. при переходе на Win64 по сравнению с предыдущим лучшим своим результатом в Win32 удалось увеличить задействованные в программе ресурсы (память и стек) в 16 раз! Поскольку сами объекты теста (контексты вызовов, адреса возврата и возвращаемое значение) тоже увеличились с 4 до 8 байт, абсолютно использованные ресурсы (в байтах) увеличились по сравнению с Win32 даже в 32 раза.
Конечно, при этом тест считается не быстро из-за недостаточного размера физической памяти. Кстати, на этом же ноутбуке можно было бы в принципе выполнить и тест с базовым значением 32, но для этого пришлось бы освободить весь 250 Гбайтный диск для файла подкачки страниц (нужно более 200 Гбайт). Очевидно, что следующие рекорды нужно ставить не на домашних компьютерах. Ну, или подождать, пока ресурсы домашних компьютеров не достигнут соответствующих величин.
Наверняка у читателя назрел вопрос: зачем было нужно это соревнование автора с неведомыми ему соперниками? И не напоминает ли оно соревнование «людоедки» Эллочки с дочерью миллионера Вандербильда? Нет, не напоминает. Потому, что решение сложной задачи использования всех возможных ресурсов компьютера (пусть даже эти ресурсы и довольно скромны по современным понятиям), позволяет использовать затем эти же приемы в реальных задачах, о чем я уже и писал в предыдущей статье (часть 1).
В моем случае, приемы работы с «большими» массивами, размещенными к тому же в нескольких областях памяти, пригодились впоследствии при обработке больших объемов картографических данных. С помощью теста Кнута я научился реально использовать в программе всю доступную память.
И при достижении наилучших результатов элемент состязательности весьма важен. Поэтому призываю всех принять участие в «чемпионате» по выполнению теста Кнута. Как показывает мой опыт, время, потраченное на разработку новых приемов использования доступной памяти и стека, не пропадает даром.
P.S. Некоторые коллеги говорили мне, что, мол, время потрачено зря, результат теста Кнута, даже рекордный, можно легко вычислить и не прибегая к собственно выполнению алгоритма. Конечно можно, причем можно сразу вычислить результат теста для такого показателя, для расчета которого современным средствам потребуется больше времени, чем существует Вселенная. Но конечное число теста – лишь квитанция, что он выполнен правильно, т.е. всю используемую память алгоритм обошел в правильном порядке. Именно так воспринимали этот тест (рекурсия, но, главное, сколько можно занять памяти) еще в Советском Союзе [4].
Литература
1. Donald Knuth (July 1964). «Man or boy?». http://www.chilton-computing.org.uk/acl/applications/algol/p006.htm. Retrieved Dec 25,2009
2. http://rosettacode.org/wiki/Man_or_boy_test
3. Д.Ю.Караваев «К вопросу о совершенствовании языка программирования» RSDN Magazine #4 2011
4. https://keldysh.ru/papers/2013/prep2013_29.pdf


chemistmail
А можно просто формулу?
Ну или аналог на Python?
чет любопытно прям стало, а алгол прочитать чет не получается ))
Dukarav Автор
по ссылке [2] на розетте тест на 100 языках, выбирайте и запускайте
chemistmail
но пашарам )
спасибо.
maxzhurkin
только это не ссылка