Поздравляю Хабр и Хаброжителей с Новым 2021 годом и дарю всем нам вот такую незатейливую и приятную Функциональную Ёлку (fЁлка). В этой статье я рассказываю как сделать ёлочку на мониторе за 10 минут. Свою вторую статью я посвящу тому, как "слепить" снеговика, положить подарки под ёлку и всё это припорошить сверху снегом.
Базовая идея
Весь рисунок - это набор математических функций от двух аргументов, x и y. Все они так или иначе базируются на SDF. Для рисования графиков использовался desmos.com.
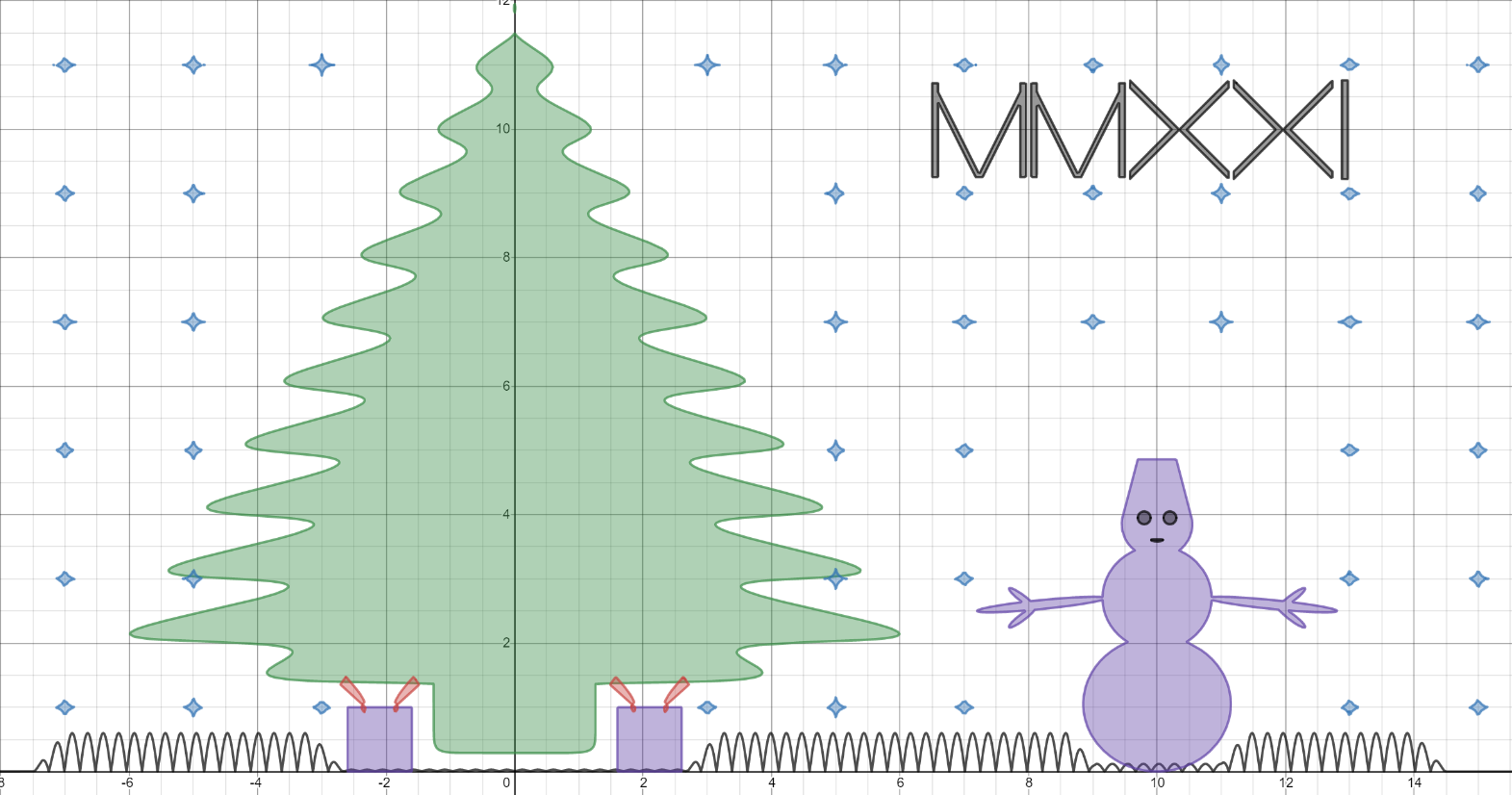
Базовые функции
Ограничение нуля

Эллипс

Ёлка
Опишем основу ёлки

Добавим ветви
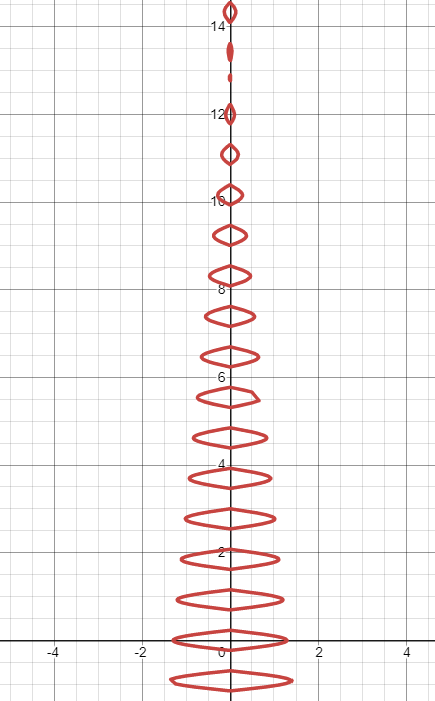
Пригнём кончики ветвей к земле

Ограничим ель сверху
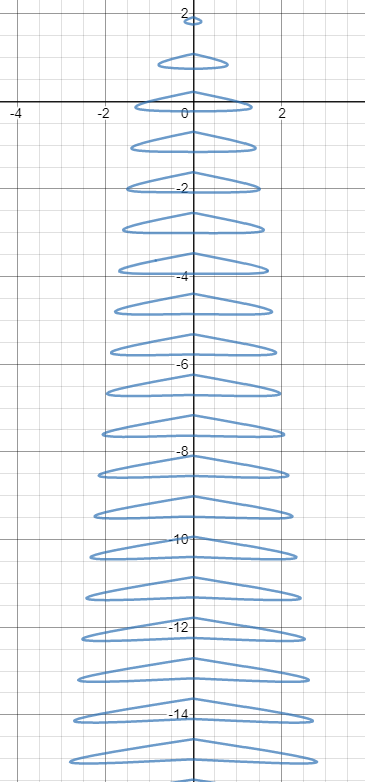
Ель съехала вниз, это исправится позднее
Параллельный ход: ограничение снизу
Ограничитель
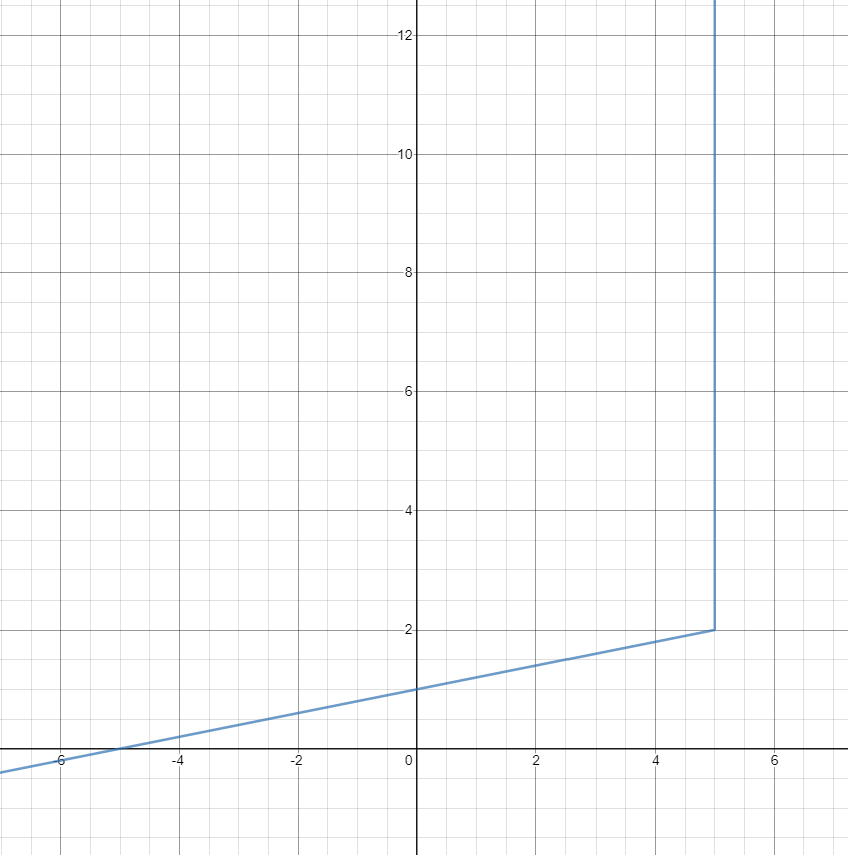
Итог данного этапа
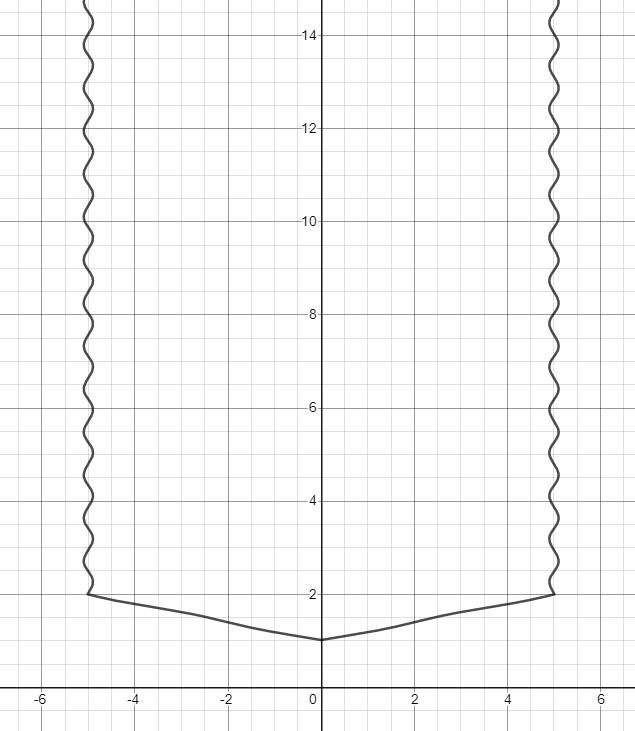
Комбинируем

Финальный штрих
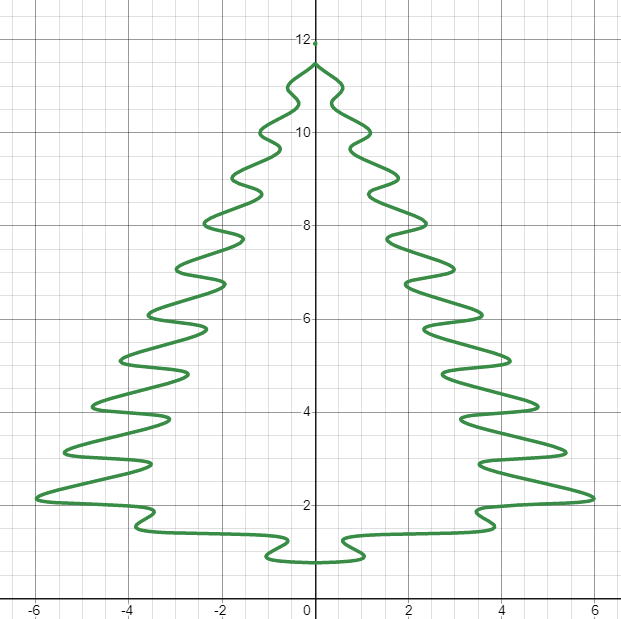
Займёмся стволом
Эллипс с более острыми углами
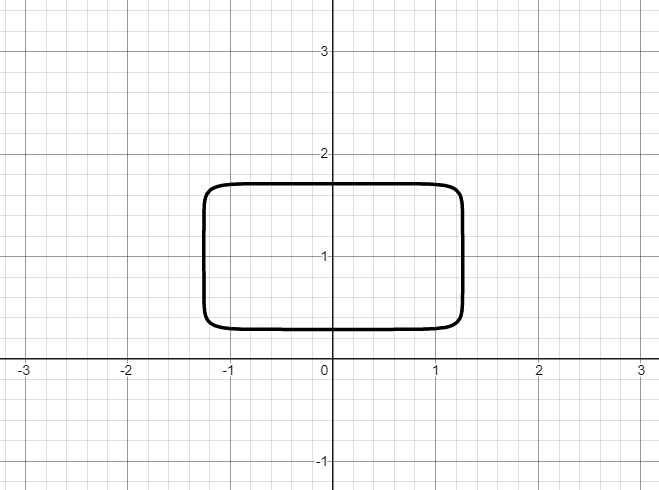
Объединение объектов
Объединение, пересечение и вырезание базируются на простейшей операции min(a, b). В зависимости от знаков перед a и b получаются различные булевы операции.
Листва - a(xy), ствол - b(xy)

Финал

Все формулы для вставки в desmos.com
a=2-0.2\cos\left(6.8y+0.7\left|x\right|\right)\left(y-13\right)-2\left|x\right|-0.51\left(y+\left|y\right|\right)+5\left(y-\left|y-2\right|\right)
b\ =\ 0.1x^{10}+30\left(y-1\right)^{10}-1
\min\left(-a,\ b\right)\le0
Продолжение следует...


Quiensabe
Nehc
Поэлементно впечатляет не слишком. ) Понятно, что практически любой сложный объект можно разложить на относительно простые составляющие, которые можно описать математически.
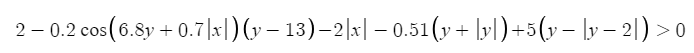

Что понравилось в исходном посте с елкой:
Это собственно математическая формула елки (по мне так и с таким «стволом» норм!):
ОДНА формула. ;) Прикольно, как по мне…
rurulik
Это да, Ёлка из поста одной формулой заслуживает внимания) Может есть другие варианты формул для будущей новогодней красавицы?)
VPryadchenko
В конце концов, лемнискатой можно что угодно нарисовать)
sergeymolchanovsky
Не отображаются некоторые символы в формулах.
GeMir
Desmos — это «русифицированная» версия GeoGebra?
RigelGL Автор
Я пробовал GeoGebra. В браузере она тормозит, некорректно парсит формулы, например ||x|-1| (\left|\left|x\right|-2\right|), не везде работает Ctrl+Z. Поэтому я выбрал Desmos. Единственное чем GeoGebra лучше Desmos'a лично для меня — возможностью строить трёхмерные уравнения.