Старая-старая школьно-студенческая задача... Дан массив целых чисел. Требуется найти m его максимальных (или минимальных) элементов. Когда я задаю эту задачу учащимся, то почти в каждой группе находятся "умельцы", решающие ее с помощью сортировки. В самом деле, это ведь так просто: сортируем массив по убыванию (вручную или подходящей библиотечной функцией) и просто берем m первых элементов. Такое решение всегда казалось мне алгоритмическим варварством - найти m максимумов достаточно просто за один проход массива; сортировка существенно сложнее. И однажды я решил исследовать сей вопрос вычислительными экспериментами. Результаты этих экспериментов я и предлагаю вашему вниманию. Не исключено, что кому-то результаты помогут и в практической работе. Намекну - интуиция меня в целом не подвела.
Spoiler
Без сортировки задача может быть решена, например, так. Создаем рабочий массив длины m и заполняем его начальными значениями. В общем случае можно в качестве такого значения выбрать минимальное значение int/integer для соответствующей среды программирования. А если известна нижняя граница значений исходного массива, то можно взять любое число, меньшее этой границы.
Итак рабочий массив заполнен одинаковыми значениями. Теперь берем элемент за элементом исходного массива и вставляем его в нужное место рабочего массива. При этом длину рабочего массива сохраняем равной m (после вставки последний элемент пропадает). Если очередной элемент меньше последнего значения рабочего массива, то он просто пропускается. Этот процесс имеет вычислительную сложность O(nm). Тогда как сортировка в лучшем случае описывается асимптотикой O(n*og(n)). Асимптотики показывают, как ведет себя функция (в данном случае - время сортировки) при стремлении параметров к бесконечности. Можно сказать, что время описанного алгоритма при стремлении n к бесконечности задается формулой t1=k1*O(n), а время сортировки t2=k2*O(n*log(n)). Здесь k1 и k2 - некие константы, зависящие от процессора, языка программирования, операционной системы и других факторов.
Я построил три системы тестов (для Питона, Java и VBA). Все тесты устроены по сути одинаково: строились массивы возрастающих размеров, заполнялись случайными числами задаваемого диапазона, сортировались с фиксацией времени и прогонялись через описанный выше алгоритм тоже с фиксацией времени. Каждый тест повторялся 10 раз и время усреднялось. В Питоне и Java использовалась встроенная сортировка, в VBA - реализация QuickSort.
Питон
Ниже показан код питоновских тестов.
import time
from random import randint
def max_n_1(arr,n):
return sorted(arr,reverse=True)[0:n]
def max_n_2(arr,n):
res=[-1 for _ in range(n)]
for x in arr:
if x > res[n-1]:
i=n-1
j=i-1
while(j>=0 and res[j]<x):
res[i]=res[j]
i=i-1
j=j-1
res[i]=x
return res
def start():
k=10
n=10000
print("k=",k)
while(n<=500000):
print("n=",n,end=' ')
t1=0.0
for i in range(10):
arr=[randint(1,2000) for _ in range(n)]
start_time = time.time()
z1=max_n_1(arr,k)
fin_time = time.time()
t1=t1+(fin_time-start_time)
print(t1/10.0,end=' ')
t2=0.0
for i in range(10):
arr=[randint(1,2000) for _ in range(n)]
start_time = time.time()
z2=max_n_2(arr,k)
fin_time = time.time()
t2=t2+(fin_time-start_time)
print(t2/10.0)
n+=10000
start()
Размеры массива менялись от 10 до 500 тыс. элементов с шагом 10 тыс. Было выполнено два прогона: определение пяти и десяти максимумов. Результат для 10 максимумов показан ниже.
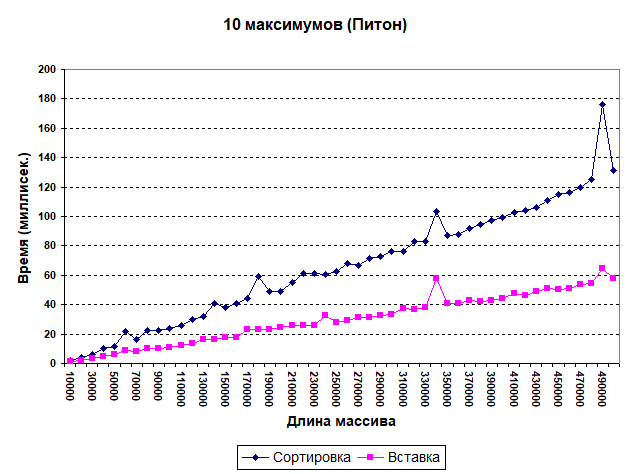
Время здесь приведено в миллисекундах. Что видим? Сортировка отстает (на краю интервала - вдвое). Для пяти максимумов картина аналогична. И надо заметить, что хотя питоновская сортировка очень эффективна, простой алгоритм оказывается быстрее. Заметны резкие провалы в производительности (зубцы на графиках). Они, вероятно, объясняются влиянием внутренних процессов (типа сборки мусора). Это же замечание относится и к другим графикам.
Java
Код тестов выглядел так:
import java.util.*;
class Start
{
public static void main(String [] args)
{
Random random = new Random();
Scanner inp = new Scanner(System.in);
long startTime,endTime,tot1,tot2;
int i,a,b,n,m,x,ii,jj,u;
a=1;
b=3000; // диапазон случайных чисел [a,b]
m=10;
System.out.println(a+" "+b+" "+m);
for (n=50000; n<=5000000; n+=50000)
{
int arr[] = new int[n];
int ma[] = new int[m];
tot1=0;
for (u=0; u<10; u++)
{
for (i=0; i<n; i++)
{
arr[i]=a+random.nextInt(b-a+1);
}
startTime = System.currentTimeMillis();
Arrays.sort(arr);
endTime = System.currentTimeMillis();
tot1=tot1+(endTime-startTime);
}
tot2=0;
for (u=0; u<10; u++)
{
for (i=0; i<n; i++)
{
arr[i]=a+random.nextInt(b-a+1);
}
startTime = System.currentTimeMillis();
for (i=0; i<m; i++) ma[i]=-999999;
for (i=0; i<n; i++)
{
x=arr[i];
if (x >= ma[m-1])
{
ii=m-1;
jj=ii-1;
while(jj>=0 && ma[jj]<x)
{
ma[ii]=ma[jj];
ii--;
jj--;
}
ma[ii]=x;
}
}
endTime = System.currentTimeMillis();
tot2=tot2+(endTime-startTime);
}
System.out.println(n+" "+tot1+" "+tot2);
}
}
}Здесь размер массива тоже менялся от 10 тыс. до 500 тыс. элементов. Время - в миллисекундах. Результат оказался весьма похожим на питоновский (только сортировка Javа, увы, медленнее).

VBA
В этом языке нет универсальной встроенной сортировки (можно, правда, сортировать ячейки листа, но в этом случае будут велики накладные расходы, связанные с загрузкой и выгрузкой данных). Поэтому пришлось реализовать QuickSort вручную. Все это выглядит так:
Private Declare Function GetTickCount Lib "kernel32" () As Long
'::: Собственно сортировка
Sub QSort(A() As Long, Optional b As Long = 1, Optional e As Long = 0)
If b > e Then Exit Sub
i& = b
j& = e
w& = A((i& + j&) / 2)
Do While (True)
Do While (A(i&) < w&)
i& = i& + 1
Loop
Do While (A(j&) > w&)
j& = j& - 1
Loop
If i& <= j& Then
Tmp& = A(i&)
A(i&) = A(j&)
A(j&) = Tmp&
i& = i& + 1
j& = j& - 1
End If
If i& > j& Then Exit Do
Loop
If j& > b Then QSort A, b, j&
If i& < e Then QSort A, i&, e
End Sub
'::: Проверка успешности сортировки
Function check(X() As Long) As Boolean
n& = UBound(X)
For i& = 1 To n& - 1
If X(i& + 1) < X(i&) Then
Debug.Print "Err! i=" + CStr(i&)
check = False
Exit Function
End If
Next i&
check = True
End Function
'::: Вставка в упорядоченный массив
Sub ins_in_arr(X As Long, A() As Long, n As Integer)
If X < A(n) Then Exit Sub
For i% = 1 To n
If X > A(i%) Then
For j% = n To i% + 1 Step -1
A(j%) = A(j% - 1)
Next j%
A(i%) = X
Exit Sub
End If
Next i%
End Sub
'::: Собственно тест
Sub test()
Const sz = 500
Dim X() As Long
Dim Ma(1 To sz) As Long
Randomize
ooo& = 1
For n& = 10000 To 500000 Step 10000
t1# = 0
For nc% = 1 To 10
ReDim X(1 To n&) As Long
For i& = 1 To n&
X(i&) = Rnd() * 5000
Next i&
s1& = GetTickCount
For i& = 1 To sz
Ma(i&) = -2147483647
Next i&
For i& = 1 To n&
ins_in_arr X(i&), Ma, 10
Next i&
s2& = GetTickCount
t1# = t1# + s2& - s1&
Next nc%
Cells(ooo&, 1).Value = n&
Cells(ooo&, 2).Value = t1# / 10
t2# = 0
For nc% = 1 To 10
ReDim X(1 To n&) As Long
For i& = 1 To n&
X(i&) = Rnd() * 5000
Next i&
s1& = GetTickCount
QSort X, 1, n&
s2& = GetTickCount
If Not check(X) Then
MsgBox "Ошибка при сортировке!"
Exit Sub
End If
t2# = t2# + s2& - s1&
Next nc%
Cells(ooo&, 3).Value = t2# / 10
ooo& = ooo& + 1
Next n&
End SubНа каждом витке цикла корректность сортировки проверяется. Время проверки, естественно, не включается в общий хронометраж. Набор исходных данных тот же - от 10 до 500 тыс. целых чисел. Получает, в общем, похожая картина:
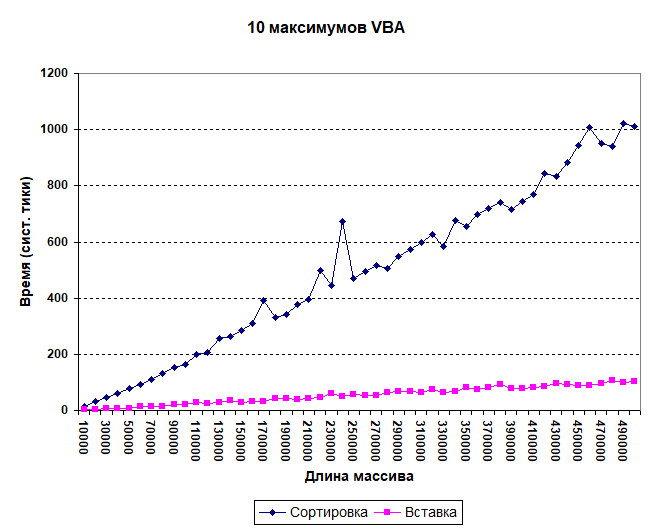
Представляет некоторый интерес изучить зависимость времени от количества искомых максимумов (при фиксированном размере массива). Здесь, очевидно, сортировка будет тем выгоднее, чем больше максимумов требуется найти. А вставка в упорядоченный массив будет тем медленнее, чем массив больше.
Самым невыгодным случаем будет являться, как ни странно, входной массив, уже упорядоченный по возрастанию. В этом случае количество сравнений при вставке достигнет максимума и будет равно n*m. Массив, упорядоченный по убыванию, напротив, весьма выгоден. Число сравнений здесь будет ~ m+n.
Описанный в самом начале статьи алгоритм, можно ускорить, если вместо простого упорядоченного массива использовать древовидную или пирамидальную структуру. Именно так и реализована в Питоне в модуле heapq функция nsmallest.
Для небольших массивов (несколько тысяч элементов и менее) разница в подходах представляется несущественной. И если нужно быстро написать код, то сортировка - вполне приемлемое решение. Для больших массивов выгоднее от сортировки отказаться.
Вот и все, что я хотел рассказать об этой задаче. Спасибо, что дочитали до конца. С наступившим 2021-м годом!



DistortNeo
Тут всё зависит от сценария использования, величин
nиm. При большихmможно пойти ещё дальше и вместо сортировки вставками использовать оптимизированную структуру, например, кучу.P.S. А преждевременная оптимизация — зло. Ведь куда проще написать (C#):
чем придумывать велосипед, который ещё надо реализовывать и тестировать.
Это я сагрился на "умельцы" и "алгоритмическое варварство".
catstail1954 Автор
«использовать оптимизированную структуру, например, кучу» — о чем я и написал в самом конце.
«Ведь куда проще написать» — конечно. Но что бы вы делали без C#? Вызвать библиотечную функцию — это одно, уметь самому реализвать ее функциональность — другое.
Dair_Targ
Изобретали бы программные библиотеки — вот что бы делали. Алгоритмы- алгоритмами, но писать свою реализацию должно быть крайним выходом.
catstail1954 Автор
«Изобретали бы программные библиотеки» — так это труднее, чем вызвать библ. функцию
Dair_Targ
Может и труднее, но это нужно сделать один раз.
Перед тем, как называть работу учеников "варварством" предложили бы им проанализировать оба подхода как с алгоритмической точки зрения, так и с точки зрения затрат на реализацию (включая поиск ошибок).
catstail1954 Автор
Что я и сделал.