Сэмплирование Томпсона — это один из самых сложных способов решения задачи «многорукого бандита».

Задача

Маленький Робот потерялся в торговом центре. С помощью обучения с подкреплением мы хотим помочь ему найти свою маму. Но прежде чем он начнёт её искать, ему нужно подзарядиться от набора розеток, каждая из которых даёт разное количество энергии.

С помощью стратегий из задачи про многорукого бандита нам нужно найти лучшую розетку в кратчайшие сроки, чтобы Маленький Робот подзарядился и отправился в путь.

Маленький Робот вошёл в комнату подзарядки. В ней 5 розеток, каждая выдаёт разное количество энергии. Нужно, чтобы Маленький Робот как можно быстрее зарядился, поэтому необходимо найти лучшую розетку и подключиться к ней.

Эта задача аналогична задаче про многорукого бандита, за исключением того, что вместо поиска игрового автомата, дающего максимальный выигрыш, мы ищем розетку с наилучшим объёмом энергии.

Сэмплирование Томпсона

Во всех методах, которые мы ранее рассматривали, действия выбирались на основе текущих средних значениях вознаграждений, получаемых за эти действия. Сэмплирование Томпсона (иногда его называют алгоритмом байесовых бандитов) работает иначе: вместо уточнения прогноза среднего вознаграждения она расширяет его, чтобы построить вероятностную модель из полученных вознаграждений, а затем выбрать на её основе действие.

В этом случае не только повышается точность прогнозирования возможного вознаграждения, так ещё и модель оценивает некую достоверность этого вознаграждения, и эта достоверность растёт по мере сбора данных. Такой процесс обновления прогноза с появлением новых доказательств называется байесовским выводом (Bayesian Inference).

Сэмплирование Бернулли-Томпсона

Давайте в качестве введения, и чтобы легче было работать, упростим задачу с поиском розетки. Вместо того, чтобы каждая розетка возвращала разное количество заряда, пусть они либо заряжают, либо нет. Тогда у вознаграждения будет два возможных значения: 1 — розетка заряжает, 0 — розетка не заряжает. Если у случайной величины лишь два возможных значения, её поведение можно описать с помощью распределения Бернулли.

Теперь вместо количества энергии в розетках меняется вероятность заряжания как такового. Нам нужно найти розетку с максимальной вероятностью заряжания, а не розетку с максимальным количеством энергии.

Итак, при сэмплировании Томпсона получается модель вероятностей вознаграждения. Когда доступность вознаграждения является бинарной (как в этом случае, да или нет), идеальной моделью для такой вероятности является бета-распределение. Подробнее о взаимосвязи бета-распределения и распределения Бернулли читайте здесь.

Бета-распределение зависит от двух параметров: и . Проще говоря, это счётчики числа успехов и неудач. Также у бета-распределения есть усреднённое значение, вычисляемое как: 

Изначально мы не знаем, какова вероятность наличия энергии в какой-либо розетке, потому можно присвоить альфе и бете значение 1, что даст нам равномерное распределение (на иллюстрации 1 показано красным). Это начальное предположение называется априорной вероятностью: вероятность возникновения какого-то события до того, как мы получили какие-либо сведения о нем; в данном случае она представлена бета-распределением

Проверив розетку и получив вознаграждение, мы можем скорректировать наши ожидания того, что розетка работает. Такая новая вероятность после получения каких-то сведений называется апостериорной вероятностью. Она тоже представлена бета-распределением, но теперь мы обновили значения и на основе полученного вознаграждения.

Если розетка работает, то вознаграждение равно 1, и — счётчик успехов — увеличивается на 1. - счётчик неудач — не растёт. Если же мы не получим вознаграждение, то не изменится, а увеличится на 1. Чем больше мы собираем данных, тем сильнее бета-распределение начинает отличаться от прямой линии и становится всё более точной моделью вероятности усреднённого вознаграждения. Поддерживая значения и , алгоритм сэмплирования Томпсона может описать ожидаемое среднее вознаграждение и уровень его достоверности.

В отличие от жадного алгоритма, в котором на каждом временном шаге выбирается действие с наивысшим ожидаемым вознаграждением, даже если достоверность ожидания невысока, сэмплирование Томпсона берёт образцы из бета-распределения каждого действия, и выбирает действие с наивысшим возвращённым значением. Поскольку редко пробуемые действия имеют широкие распределения, (см. синюю кривую на иллюстрации 1), то у них больше диапазон возможных значений. Поэтому розетка, у которой сейчас низкое ожидаемое среднее вознаграждение, но которая тестировалась реже розетки с более высоким средним ожиданием, может вернуть большее выборочное значение и будет выбрана на следующем временном шаге.

На вышеприведённом графике синяя кривая имеет более низкое ожидаемое среднее вознаграждение, чем у зелёной кривой. Поэтому при жадном алгоритме будет выбрана зелёная розетка, а синяя никогда не будет выбрана. А сэмплирование Томпсона эффективно учитывает полную ширину кривой, которая у синей розетки может быть шире, чем у зелёной. В этом случае выбор может быть сделан в пользу синей розетки.

Чем чаще используется розетка, тем выше достоверность её ожидаемого среднего. Это отражено в сужении распределения вероятности, и выборочное значение будет браться из диапазона значений, которые ближе к реальному среднему (см. зелёную кривую на иллюстрации 1). В результате исследование (explore) уменьшается, а использование (exploit) растёт, потому что алгоритм начинает чаще выбирать розетки с более высокой вероятностью получения вознаграждения.

С другой стороны, розетки с низким ожидаемым среднем будут выбираться реже и в конце концов будут быстро выброшены из процесса выбора. Поэтому их истинное среднее может и не быть найдено. А поскольку нас интересует лишь розетка с наивысшей вероятностью получения вознаграждения, причём найти её нужно как можно скорее, то нас не волнует, что мы так и не получим всю информацию о плохо работающих розетках. 

Реализация розеток по Бернулли

Воспользуемся базовым классом розеток, поверх которого добавим особую функциональность изучаемого алгоритма. Затем прогоним этот новый класс через набор экспериментов с помощью тестовой программы для всех бандитских алгоритмов. Подробное описание базового класса розеток и тестовой системы дано в одной из предыдущих статей, а весь код лежит на Github.

Покажу реализацию сэмплирования Бернулли-Томпсона на примере класса BernoulliThompsonSocket:

class BernoulliThompsonSocket( PowerSocket ):
    def __init__( self, q ):             
                
        self.? = 1  # the number of times this socket returned a charge        
        self.? = 1  # the number of times no charge was returned
        
        # pass the true reward value to the base PowerSocket             
        super().__init__(q)          
    
    def charge(self):        
        """ return some charge with the socket's predefined probability """
        return np.random.random() < self.q
                    
    def update(self,R):
        """ increase the number of times this socket has been used and 
            update the counts of the number of times the socket has and 
            has not returned a charge (alpha and beta)"""
        self.n += 1    
        self.? += R
        self.? += (1-R)
        
    def sample(self):
        """ return a value sampled from the beta distribution """
        return np.random.beta(self.?,self.?)

В этом классе мы инициализируем и со значениями 1, чтобы получить равномерное распределение. Затем при обновлении мы просто увеличиваем если розетка возвращает вознаграждение, а в противном случае увеличиваем .

Функция sample выводит значение из бета-распределения, используя в качестве параметров текущие значения и .

Результаты экспериментов

На иллюстрации 2 показано изменение бета-распределения для каждой розетки, когда мы используем розетки с более простой вероятностью. Чтобы было проще, мы уменьшили количество розеток до трёх. Их истинные вероятности при проверке работоспособности равны 0,3 (зелёная), 0,7 (красная) и 0,8 (синяя).

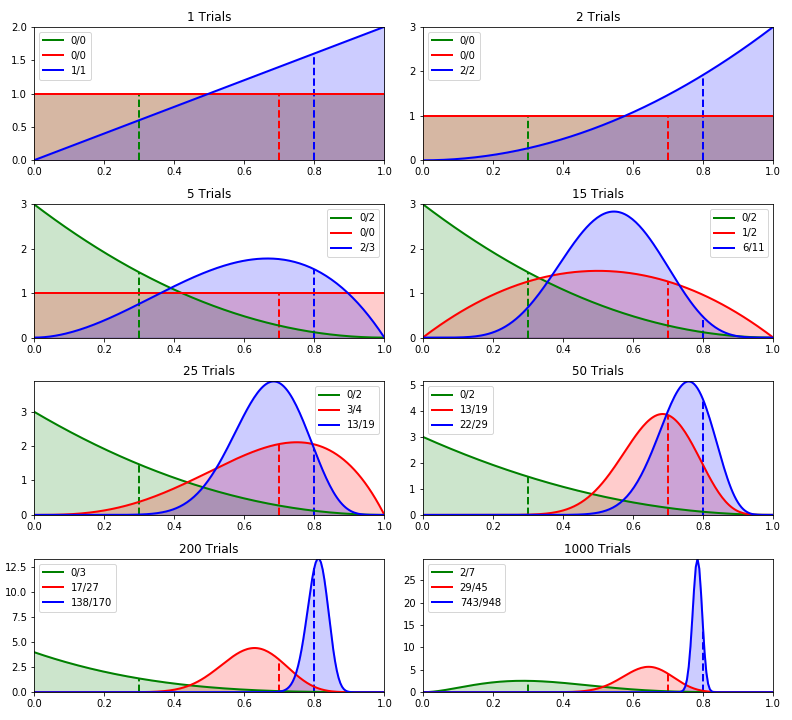
Истинные средние значения 0,3, 0,7 и 0,8 показаны пунктирами. В легенде указано общее количество попыток для каждой розетки и количество успешных. Что можно отметить, глядя на эти графики:

• На временном шаге 0 (не показан) все бета-распределения будут иметь и равными 1, чтобы было равномерное распределение.

• Поскольку начальное распределение у всех розеток одинаковое, на временном шаге 1 синяя была выбрана произвольно. При проверке она дала вознаграждение, поэтому её увеличилась на 1, кривая плотности вероятностей сместилась вправо. Зелёная и красная розетки ещё не были проверены, поэтому их распределения остались равномерными (зелёная линия не видна под красной).

• На втором временном шаге снова выбрана синяя розетка, и она снова вернула вознаграждение. Её график ещё немного сместился вправо, потому что розетка проверена дважды и оба раза вернула вознаграждение. Ещё есть вероятность, что она будет возвращать вознаграждение каждый раз.

• К пятому разу ещё раз была выбрана синяя, но на этот раз она не дала вознаграждения. Поэтому вероятность того, что розетка всегда будет вознаграждать, упала до 0 (при вероятности = 1.0). С другой стороны, зелёная розетка была протестирована дважды и пока не вернула вознаграждение, поэтому кривая плотности вероятностей сдвинулась влево с максимальным значением = 0, потому что ещё есть шанс, что розетка никогда не вернёт вознаграждение.

• К 15 разу пару раз была проверена красная розетка. Поскольку она один раз вернула вознаграждение, её ожидаемая средняя вероятность вознаграждения равна 0,5. На этом этапе синяя розетка была проверена 11 раз, из них 6 раз она вернула вознаграждение, так что её ожидаемая вероятность вознаграждения равна 0,54. Жадный алгоритм выбрал бы синюю розетку, но поскольку мы проверяли красную реже синей, её кривая плотности вероятностей гораздо шире, так что у розетки хорошие шансы быть выбранной вместо синей.

• Чем больше проверяется розетка, тем выше доверенность её ожидания и тем у?же становится её кривая плотности вероятностей. Лучшая розетка потом будет использоваться чаще, а проверка менее оптимальных розеток сойдёт на нет. Такое поведение видно в конце нашего теста, когда синяя розетка выбирается намного чаще остальных. Также видно, что зелёная розетка вернула вознаграждение в двух попытках. Следовательно, теперь отсутствует вероятность, что розетка никогда не вернёт вознаграждение, поэтому график падает до 0. 

• Наконец, видно, что у красной и синей розеток кривые плотности вероятностей не находятся прямо на их истинных средних вероятностях. Если бы тест прогнали ещё несколько раз, то синяя кривая в результате совпала бы с истинным средним значение, но у красной будет гораздо меньше попыток (если вообще будут), так что её истинное значение может остаться ненайденным. Как упоминалось выше, это не проблема, потому что нас интересует только лучшая розетка, а не истинные средние значения других розеток.

Сэмплирование Гаусса-Томпсона

Упрощённая задача с розетками — хороший пример для изучения сэмплирования Байеса-Томпсона. Но если применять этот метод для решения настоящей задачи, в которой розетки не двоичны, а возвращают разное количество энергии, нам нужно кое-что изменить.

Выше мы моделировали поведение розеток с помощью бета-распределения. Это было сделано потому, что упрощённые розетки имели два возможных значения — работает или не работает, и их можно было описать с помощью распределения Бернулли. При извлечении значения из этого распределения (значение правдоподобия) оно умножается на значение, извлечённое из бета-распределения (априорная вероятность), а получившееся значение (апостериорная вероятность) также имеет бета-распределение. Если правдоподобие, умноженное на априорность, даёт апостериорность с тем же типом распределения, что и у априорности, то такая априорность называется сопряжённым априорным распределением.

В нашей стандартной задаче каждая розетка возвращает реальное значение, описываемое нормальным распределением. Если мы считаем, что нам известна дисперсия розетки (которая равна 1, потому что мы используем в коде неизменённую версию функции numpy randn), то из таблицы на Википедии мы узнаём, что у сопряжённой априорности тоже нормальное распределение. Если же нам неизвестна дисперсия распределения, или если мы используем другое распределение, то нам просто нужно выбрать в таблице одну из других сопряжённых априорностей и скорректировать соответствующим образом наш алгоритм.

Поэтому мы можем смоделировать результат проверки розетки с помощью нормального распределения и постепенно улучшать модель, обновляя её среднее и параметры дисперсии. Если вместо дисперсии воспользоваться точностью (тау), где точность равна единице, делённой на дисперсию (точность = 1/дисперсия), то мы можем использовать простые правила для обновления среднего и точности :

где:

• — точность реального результата проверки розетки, которая в нашем случае равна 1;

• — количество проверок розетки;

• — результат, полученный при каждой i-проверке розетки (эквивалентно вознаграждению , которое мы использовали до этого момента;

• — ожидаемое среднее (среднее распределения, использованного для моделирования результата);

• — полная точность распределения, использованного для моделирования результата.

На первый взгляд выглядит пугающе, но тут лишь говорится, что у на есть два параметра и , которые мы будем обновлять при каждой проверке розетки, как и в случае с и для розеток Бернулли. Только там эти параметры представляли количество успешных и неудачных проверок розеток, а и представляют ожидаемые среднее и точность, отражая достоверность ожидаемого среднего значения.

Можно сделать ещё пару упрощений:

• Мы знаем, что количество возвращаемой розеткой энергии имеет дисперсию 1, поэтому точность тоже равна 1. Следовательно, обновление точности розетки представляет собой просто где n — количество проверок розетки, так что при каждой проверке мы просто увеличиваем точность розетки на 1.

• У ожидаемого среднего числитель содержит сумму всех результатов проверки розетки, умноженную на . Оставлять сумму вознаграждений нецелесообразно, потому что она может разрастись до очень больших размеров. Однако в нашей базовой реализации розеток мы всегда вычисляем — ожидаемое значение действия на временном шаге t, которое вычисляется так
  
  

• В этом уравнении — вознаграждение, получаемое на каждом временном шаге при выполнении действия a. Оно идентично термину который использовался выше в обновлённом выражении. Поэтому можно просто заменить в обновлённом выражении сумму на и получим
  
  

Этими упрощениями мы избавились от страшной математики! Теперь очевидно, что нам нужно лишь сохранять ожидания среднего, а также точности вознаграждения для всех розеток, а затем применять два простых правила для обновления этих значений. А когда напишете эти уравнения в коде, всё станет ещё понятнее.

Реализация розеток Гаусса

Ниже представлен код для сэмплирования Гаусса-Томпсона. Обратите внимание, что в этом коде мы заменили сумму всех вознаграждений на self.n * self.Q. Это даёт нам точно такое же значение, но без необходимости суммировать все вознаграждения, что может оказаться очень громоздким вычислением.

class GaussianThompsonSocket( PowerSocket ):
    def __init__(self, q):                
                
        self.?_0 = 0.0001  # the posterior precision
        self.?_0 = 1       # the posterior mean
        
        # pass the true reward value to the base PowerSocket             
        super().__init__(q)         
        
    def sample(self):
        """ return a value from the the posterior normal distribution """
        return (np.random.randn() / np.sqrt(self.?_0)) + self.?_0    
                    
    def update(self,R):
        """ update this socket after it has returned reward value 'R' """   

        # do a standard update of the estimated mean
        super().update(R)    
               
        # update the mean and precision of the posterior
        self.?_0 = ((self.?_0 * self.?_0) + (self.n * self.Q))/(self.?_0 + self.n)        
        self.?_0 += 1     

Важно отметить:

• Функция sample возвращает не Q (ожидаемое значение вознаграждения розетки), а выборочное значение из нормального распределения, которое мы используем для моделирования результата розетки (апостериор со средним self.?_00 и точностью self.?_0).

• Как и в случае с бета-распределением, которое применялось для моделирования результатов двоичных розеток, мы хотим, чтобы наше априорное распределение начиналось с близкого к равномерному, с прямой линией распределения вероятностей. Это даёт возможность вернуть выборочное значение из широкого диапазона возможных значений. Так что изначально мы задаём очень маленькую точность апостериора (self.?_0 = 0.0001). Тогда розетки, которые мы ещё не пробовали, будут выбраны с большей вероятностью, как и в случае с оптимистично-жадным алгоритмом.

Если вы вернётесь к коду базовой розетки, то увидите, что при выборе розетка возвращает количество энергии, заданное нормальным распределением поблизости от истинного среднего значения:

   def charge(self):
        """ return a random amount of charge """
        
        # the reward is a guassian distribution with unit variance around the true value 'q'
        value = np.random.randn() + self.q

В функцииchargeNumpy-функцияrandnвозвращает из нормального распределения среднего 0 и дисперсии 1 случайное значение. Добавив к нему значение истинного вознаграждения розеткиq, мы смещаем распределение среднего к реальному результату розетки. 

В функцииsampleрозеток Томпсона применяется очень похожая функция:

   def sample(self):
        """ return a value from the the posterior normal distribution """
        return (np.random.randn() / np.sqrt(self.?_0)) + self.?_0  

Только в этом случае нормальное распределение находится на апостериорном среднем self.?_0. Кроме того, randn теперь делится на квадратный корень апостериорной точности self.?_0. Помните, что точность равна единице, делённой на дисперсию. Это меняет ширину распределения, уменьшая её по мере получения новых образцов, и достоверность ожидаемого среднего растёт.

Результаты экспериментов

Как и в случае с Бернулли, мы прогнали больше 1000 попыток. Поскольку апостериорное распределение началось с почти прямой линии, каждая из пяти розеток однократно проверена в течение первых пяти попыток. В последующих попытках доминирует розетка 4 (красная кривая). К концу тестирования она превратилась в высокую тонкую кривую, центр которой лежит на значении 12 (истинное значение вознаграждения розетки), что говорит о высоком уровне достоверности этого значения.

За первые 200 проверок лишь ещё одна розетка тестировалась больше одного раза — пятая (фиолетовая кривая, с истинным вознаграждением 10). Но она проверялась лишь трижды, поэтому имеет маленькую и толстую кривую распределения, что говорит о низкой достоверности значения.

На иллюстрации 3 видно, как быстро сэмплирование Томпсона находит и использует лучшую розетку, а остальные оставляет практически без проверки. Таким образом алгоритм возвращает большое и почти оптимальное накопленное вознаграждение.

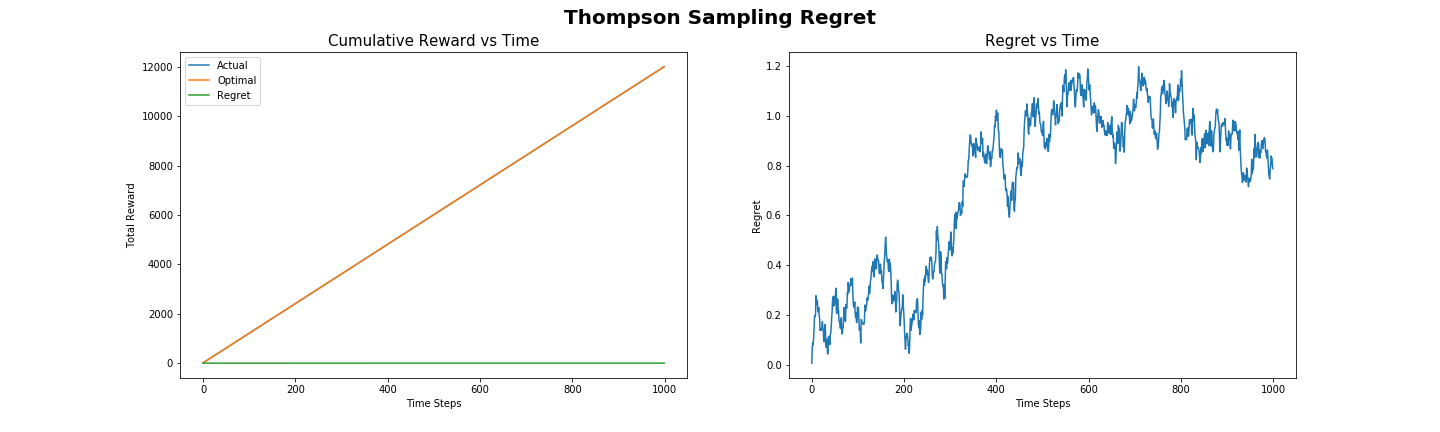
Сожаление в сэмплировании Томпсона

Сожаление (regret), получаемое при использовании сэмплирования Томпсона для решения стандартной задачи с розетками, показано на иллюстрации 4. Оно практически нулевое, это говорит о том, что почти всегда выбиралась лучшая розетка. Также сожаление можно оценить по графику «накопительное вознаграждение от времени», где реальное полученное вознаграждение настолько близко к оптимальному, что кривые почти совпадают. По кривым плотности вероятностей в сэмплировании Гаусса-Томпсона видно, что алгоритм быстро находит лучшее действие и безжалостно его использует, что даёт очень низкий уровень сожаления.

Как и в случае с алгоритмом UCB, сэмплирование Томпсона можно показать с логарифмическим сожалением, когда со временем значение сожаления падает почти до нуля. В нашем эксперименте логарифмическое падение сожаления незаметно из-за очень маленького количества действий и отдельных значений вознаграждения для каждой розетки, сожаление уже почти нулевое.

Подробнее о сэмплировании Томпсона, его применении и математическом аппарате можно почитать в книге “A Tutorial on Thompson Sampling” автора Daniel J. Russo.

Итоги

Алгоритмам для решения задачи с бандитом нужно искать компромисс между исследованием и использованием. Им нужно искать лучшие действия, при этом пытаясь воспользоваться уже полученной информацией.

В простом алгоритме, например, эпсилон-жадном (epsilon-greedy), компромисс по большей части достигается с помощью использования действия, которое сейчас даёт максимальное вознаграждение, и добавления простого исследования, а затем случайно выбирается какое-то другое действие. В более сложных решениях вроде UCB часто выбираются действия с максимальным вознаграждением, но это уравновешивается измерением достоверности. Это гарантирует проверку действий, которые редко выбирались.

Сэмплирование Томпсона предлагает иной подход. Вместо простого вычисления ожидания вознаграждения оно постепенно улучшает модель вероятности вознаграждения для каждого действия, а сами действия выбираются на основе образцов из распределения. Поэтому можно получить ожидание среднего значения вознаграждения, а также вычислить достоверность этого ожидания. Как мы видели в наших экспериментах, это позволяет быстро находить и фиксировать оптимальное действие, выдавая практически оптимальный накопленный результат.

Но является ли сэмплирование Томпсона лучшим решением задачи многорукого бандита? И что ещё важнее, стоит ли его использовать для зарядки Малыша Робота? Об этом мы расскажем в следующей статье, в которой сравним друг с другом все алгоритмы!