18.03.2021 08:16
st-fedotov 4 2700 Источник
Мы решили поделиться с Хабром заданиями из письменного экзамена в Школу анализа данных. Если вы помните высшую математику, попробуйте решить одну или несколько задач. Если нет, можно посмотреть видео- или текстовый разбор — мы постарались сделать их максимально дружелюбными. Задачи взяты из вариантов 2019 года — в этом году они, конечно, будут другими, но в разборах есть полезные факты и приёмы.

Задача 1. Предел отношения


Известно, что:

$\lim_{x \to 0} \frac {f(x)}{\sin x}= 2$


Нужно найти:

$\lim_{x \to 0} \frac {ln(1+3x)}{f(x)}$



Видеоразбор

Текстовый разбор
Для начала попробуем что-нибудь понять про f(x) и про её поведение в окрестности нуля. Умножим и разделим на синус, чтобы получить известное. Запишем:

$f(x)= \frac{f(x)}{\sin x}\cdot \sin x$


При x, стремящемся к 0, первый множитель стремится к двойке, а второй стремится к 0. Значит, их произведение тоже стремится к нулю:

$f(x)= \frac{f(x)}{\sin x}\cdot \sin x\rightarrow 2\cdot0=0(x \rightarrow 0)$


Посмотрим на то частное предела, которое надо найти:

$\frac {ln(1+3x)}{f(x)}$


Видно, что в знаменателе стоит нечто стремящееся к нулю. В числителе — нечто стремящееся к логарифму единицы, то есть тоже к нулю. Видна неопределённость 0/0.

Неправильное решение

Мы сразу вспоминаем правило Лопиталя. Предположим, что:

$\lim_{x \to 0} \frac {ln(1+3x)}{f(x)}=\lim_{x \to 0} \frac { \frac{3}{1+3x}}{f'(x)},$


если предел правой части существует. Зная f(x)/sin x, можно понять, чему равна производная f в нуле. В чём ошибка? Нам не сказано, что f вообще дифференцируема. Поэтому решение, использующее производные, не подходит.

Правильное решение

Напишем предел частного, которое надо найти. Постараемся в этом частном выделить f(x)/sin x, про которое мы уже что-то знаем.

$\frac {ln(1+3x)}{f(x)}=\frac {ln(1+3x)}{\sin x} \cdot \frac {\sin x}{f(x)}$


Нам известно, что предел второго множителя — ?. А предел первого множителя можно посчитать с помощью правила Лопиталя.

$\lim_{x \to 0} \frac {ln(1+3x)}{\sin x} = \lim_{x \to 0} \frac {\frac{3}{1+3x}}{cos(x)}=\frac{3/1}{1}=3$


Мы видим, что:

$\frac {ln(1+3x)}{\sin x}\rightarrow3$


Следовательно, искомый предел равен ?/?.

Ответ: ?/?

Задача 2. Матрица проекции


Заполните третий столбец матрицы

$ \frac{1}{6}\begin{pmatrix}5 & -2 & ?\\-2 & 2 & ?\\ -1 & -2 & ?\end{pmatrix},$


если известно, что это матрица ортогональной проекции на некоторую плоскость.

Видеоразбор

Текстовый разбор
Обозначим матрицу как A. И для начала вспомним, что такое проекция и ортогональная проекция в частности.

Проекция

Допустим, есть трёхмерное вещественное пространство (если мы говорим о проекциях, то оно, скорее всего, вещественное). Оно разбито в прямую сумму своих подпространств U и W:

$ \mathbb{R}^3=U\oplus W$


Раз это прямая сумма, то каждый вектор единственным образом представляется в виде суммы элементов:

$\ni v=u+w, $

$u\in U, w\in W$


И проекция на U вдоль W переводит сумму u + w в вектор u. В нашем случае, поскольку это проекция на плоскость, U — двумерное, а W по соображениям размерности является одномерным, некоторой прямой. То есть если мы бы не принимали во внимание, что проекция должна быть ортогональной, то U и W можно было бы изобразить так:


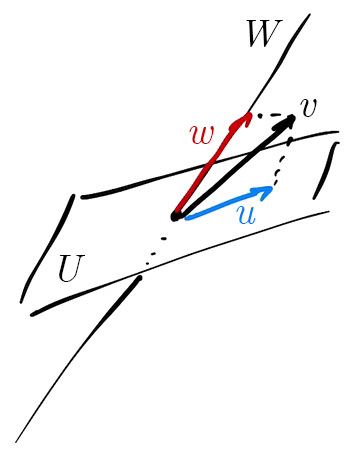
Как это связано с понятием параллельной проекции, которое, возможно, нам знакомо? Дело в том, что если построить прямую из конечной точки вектора v до конечной точки вектора u, то она будет параллельна вектору w.

Ортогональная проекция

Ортогональная проекция — это проекция, для которой второе слагаемое W прямой суммы является ортогональным дополнением к U, то есть множеством всех векторов, ортогональных к U.

$ \mathbb{R}^3=U\oplus U^{\bot}\mbox{ — ортогональная проекция на $U$}$


Первый вариант решения

Что нам ещё известно о проекциях? Возможно, мы помним какие-нибудь теоремы про них. Например, такую:

Теорема.

1) А — это матрица (простой) проекции тогда и только тогда, когда A? = A.

2) А — это матрица ортогональной проекции тогда и только тогда, когда A? = A и А является самосопряжённой: A? = А.

Здесь легко ошибиться. Видя слово «ортогональная», можно подумать, что речь идёт об ортогональном операторе, и вместо A? = А написать A? = A??. Это было бы неверно. Как правило, матрица ортогональной проекции — не ортогональная матрица хотя бы по одной простой причине: столбцы ортогональной матрицы образуют ортонормированный базис (в частности, она всегда невырождена и у неё есть обратная матрица); тогда как матрица проекции обратима, только если это тождественное отображение.

Поэтому вторая половина утверждения теоремы говорит, что A? = А. Зная это, мы легко можем симметрично отразить матрицу и найти два элемента из трёх:

$ A=\frac{1}{6}\begin{pmatrix} 5 & -2 & \color{blue}{-1}\\ -2 & 2 & \color{blue}{-2}\\ -1 & -2 & \color{blue}{x}\end{pmatrix} $


Последний оставшийся элемент x мы найдём, зная, что A? = А.

$ A=\frac{1}{6}\begin{pmatrix}\color{red}5 & -2 & -1\\ \color{red}{-2} & 2 & -2\\ \color{red}{-1} & \color{red}{-2} & \color{red}{x}\end{pmatrix}=A^2=\begin{pmatrix} & & \\ & & \\ \color{red}{[3,1]} & & \mbox{ $$ $$ $$ $$ $$ $$ $$ $$ }\end{pmatrix}$


Вычислим, например, элемент в третьей строке первого столбца. Чтобы это сделать, умножим третью строку матрицы в левой части на её первый столбец. Искомый элемент будет равен:

$ \frac{1}{36}(5(-1)+(-2)(-2)+(-1)x)=-\frac{1+x}{36}$


То есть:

$ A=\frac{1}{6}\begin{pmatrix}5 & -2 & -1\\ {-2} & 2 & -2\\ {-1} & {-2} & {x}\end{pmatrix}=A^2=\begin{pmatrix} & & \\ & & \\ -\frac{1+x}{36} & & \mbox{ $$ $$ $$ $$ $$ $$ $$ $$ }\end{pmatrix} $

$ \begin{pmatrix}\frac{5}{6} & -\frac{2}{6} & -\frac{1}{6} \\ -\frac{2}{6} & \frac{2}{6} & -\frac{2}{6} \\ -\frac{1}{6} & -\frac{2}{6} & \frac{x}{6} \end{pmatrix}=\begin{pmatrix} & \color{white}{\frac{1}{6}} & \\ & \color{white}{\frac{1}{6}} & \\ -\frac{1+x}{36} & & \mbox{ $$ $$ $$ $$ $$ $$ $$ $$ }\end{pmatrix}$

$-\frac{1}{6}=-\frac{1+x}{36}$

$x=5$


Ответ:

$\begin{matrix}-1\\-2\\5\end{matrix}$


Второй вариант решения

В первом варианте решения мы использовали нетривиальную теорему о матрицах проекции и ортогональной проекции. Представим, что мы не знаем или забыли эту теорему.

Что нам известно о плоскости U, на которую построена упомянутая в условии проекция? Вспомним, что в столбцах матрицы линейного оператора стоят образы базисных векторов: A = (Ae? Ae? Ae?). В скобках — проекции базисных векторов e?, e? и e? на U.

Проекции e? и e? — не пропорциональные векторы, они лежат в плоскости U. Значит, U — линейная оболочка первых двух столбцов матрицы A:

$U=<\frac{1}{6}\begin{pmatrix}5\\-2\\-1\end{pmatrix},\frac{1}{6}\begin{pmatrix}-2\\2\\-2\end{pmatrix}>$


Поскольку мы хотим записать базис плоскости U, то можем умножить эти векторы на любую константу, например:

$U=<\begin{pmatrix}5\\-2\\-1\end{pmatrix},\begin{pmatrix}-1\\1\\-1\end{pmatrix}>$


Мы уже знаем, что данный линейный оператор — это оператор проекции на плоскость U. Нам осталось найти Ae? — ортогональную проекцию вектора e? на U.

Вспомним, что если бы плоскость U была записана в виде линейной оболочки двух ортогональных векторов w? и w?, то было бы легко найти проекцию Ae?. Мы бы использовали формулу о том, что проекция на линейную оболочку двух ортогональных векторов — это сумма двух проекций на каждый из этих векторов:

$Ae_3=\frac{(w_1,e_3)}{(w_1,w_1)}w_1+\frac{(w_2,e_3)}{(w_2,w_2)}w_2,$


где в числителях и знаменателях стоят скалярные произведения. Эти дроби могут быть нам знакомы — они встречались в ортогонализации Грама – Шмидта, и не просто так.

С другой стороны, векторы, которые мы записали ранее, не ортогональны:

$u_1=\begin{pmatrix}5\\-2\\-1\end{pmatrix},u_2=\begin{pmatrix}-1\\1\\-1\end{pmatrix},u_1\not\perp u_2$


Но это легко исправить как раз с помощью ортогонализации Грама – Шмидта. Мы хотим построить ортогональный базис той же самой линейной оболочки для U: <w?, w?>.

В качестве вектора w? возьмём просто u?, а вектор u? поправим на проекцию u? на u?, чтобы получить w? (ортогональный по отношению к w?):


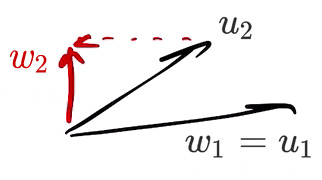
Нужно найти вектор w?. Он равен разности u? и проекции:

$w_2=u_2-\frac{(u_2,w_1)}{w_1,w_1}w_1$


Остаётся подставить это выражение и w? = u? в формулу для Ae?:

$Ae_3=\frac{(w_1,e_3)}{(w_1,w_1)}w_1+\frac{(w_2,e_3)}{(w_2,w_2)}w_2=\frac{1}{6}\begin{pmatrix}-1\\-2\\5\end{pmatrix}$


Ответ:

$\begin{matrix}-1\\-2\\5\end{matrix}$


Задача 3. Матожидание числа шаров


В корзине лежит m чёрных шаров и n красных. Мы достаём из корзины случайный шар и, если он чёрный, то заменяем его на красный, а если он красный, то кладём его обратно. Найдите математическое ожидание числа красных шаров в корзине после k итераций этой процедуры.

Видеоразбор

Текстовый разбор
Обозначим количество красных шаров в корзине после k итераций как x. Нужно найти математическое ожидание величины x.

Для начала заметим: поскольку мы кладём шар обратно в корзину, если он красный, то x = n + y, где y — количество чёрных шаров, которые стали красными после k итераций. Наверное, это упростит нам вычисления, но как именно — пока непонятно, потому что неизвестно, как искать требуемое матожидание.

Индикаторная случайная величина

Для поиска матожидания количества каких-либо объектов существует удобный инструмент — индикаторные случайные величины.

Пронумеруем чёрные шары. Для каждого j-го чёрного шара введём случайную величину, которая будет индикатором того, что j-й чёрный шар стал красным после k итераций:

$I_j=\mathbb{I}\left\{ \mbox{$j$-й чёрный шар стал красным после $k$ итераций}\right\}$


Эта случайная величина равна единице, если шар поменял цвет, и нулю, если не поменял. Следовательно, сумма таких величин будет равна количеству поменявших цвет шаров, которое мы выше обозначили как y:

$y=\sum_j I_j$


Следовательно:

$\mathbb{E}y=\sum_j \mathbb{E}I_j$


В правой части стоит сумма математических ожиданий случайной величины. Считать такие матожидания — одно удовольствие. Вспомним, что матожидание — это сумма произведений вида «значение ? вероятность этого значения». В нашем случае значений всего два: 1 и 0. Таким образом:

$\mathbb{E}y=\sum_j \mathbb{E}I_j=\sum_j (1\cdot P(I_j=1)+0\cdot P(I_j=0))=\sum_j P(I_j=1)$


Получилась сумма вероятностей того, что j-й чёрный шар поменял цвет. Посчитаем эту вероятность.

Подсчёт вероятности

Нам необходимо найти P(Ij=1). Будет удобнее перейти к отрицанию, к дополнительному событию:

$P(I_j=1)=P(\mbox{$j$-й чёрный шар стал красным})=$

$=1-P(\mbox{$j$-й чёрный шар не стал красным, а остался чёрным})=$

$=1-P(\mbox{$j$-й чёрный ни разу не вытащен})$


Чему равна вероятность, стоящая после знака минус? У нас есть k попыток вытащить шар. Поскольку попытки независимые, то вероятность после знака минус будет равна некоторому выражению в k-й степени — произведению вероятностей того, что при каждой попытке мы не вытащили данный шар.

Какова вероятность не вытащить шар в каждой конкретной попытке? Это будет дробь, в знаменателе — общее число шаров m + n. Мы должны были вытащить какой-либо шар кроме j-го. Вариантов так сделать — m + n – 1. Это выражение и будет в числителе.

$P(I_j=1)=1-\left( \frac{m+n-1}{m+n} \right)^k$


Мы нашли вероятность, что выбранный нами индикатор равен единице, — то есть вероятность, что конкретный шар поменял цвет.

Вычисление искомого матожидания

$\mathbb{E}x=\mathbb{E}(n+y)=n+\mathbb{E}y=n+\sum_j P(I_j=1)$


Все вероятности, стоящие справа под знаком суммы, — одинаковые. Поэтому сумма будет равна количеству чёрных шаров m, умноженному на вероятность, что конкретный шар поменял цвет. Эту вероятность мы нашли выше.

$\mathbb{E}x=n+mP(I_j=1)=n+m\left( 1-\left( \frac{m+n-1}{m+n} \right)^k \right)$


Ответ:

$n+m\left( 1-\left( \frac{m+n-1}{m+n} \right)^k \right)$


Задача 4. Геометрическая вероятность


Лёша и Марина договорились встретиться между 8:00 и 9:00 и вместе пойти на экзамен в ШАД. Каждый из них приходит на место встречи в случайный момент времени, ждёт 15 минут и уходит (никому не хочется опоздать на экзамен). Являются ли независимыми события «Лёша и Марина не встретились» и «хотя бы один из них пришёл после 8:45»? Время считайте непрерывным.

Видеоразбор

Текстовый разбор
Вспомним определение независимости. Два события называются независимыми, если вероятность их пересечения равна произведению их вероятностей:

$P(A \cap B)= P(A)\cdot P(B)$


Чтобы определить независимость событий A и B, нужно посчитать две вероятности в правой части. Сделать это проще всего геометрически. Представим каждое из элементарных событий (пару «время, когда пришёл Лёша» и «время, когда пришла Марина») точками квадрата со стороной 1 час.


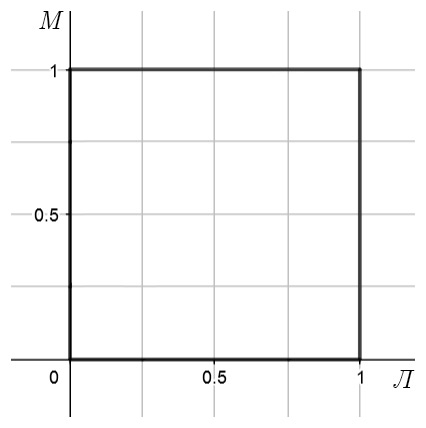
Это будет пространство элементарных событий. Мы разметили его на четвертинки, так как 15 минут от 1 часа — это и есть четверть.

Построим графическое представление каждого из событий.

Расчёт события А («Лёша и Марина не встретились»)

Какое условие накладывает событие А на координаты М и Л (они же x, y)? Оно показывает, что ребята не встретились, то есть что между приходом Лёши и Марины прошло больше четверти часа. Запишем:

$A:\left|x-y\right|>\frac{1}{4}$


Это условие можно переписать в виде совокупности:

$\left[ \begin{gathered} y<x-\frac{1}{4}\hfill\\ y>x+\frac{1}{4} \end{gathered} \right.$


Теперь можно изобразить событие А в пространстве элементарных событий:


Расчёт события B («хотя бы один из друзей пришёл после 8:45»)

Так как кто-то из пары пришёл после 8:45, то есть после трёх четвертей часа, то это можно записать следующим образом:

$B:\max (x,y)>\frac{3}{4}$


Нарисуем это событие в пространстве элементарных событий, хотя бы одно из чисел х и у больше трёх четвертей:


Как только А и B найдены, можно найти их вероятности. Чтобы найти вероятность А, нужно разделить площадь красного фрагмента на площадь всего пространства элементарных событий. Эта площадь в задаче равна единице. Красный фрагмент состоит из двух треугольников со стороной три четверти. Считаем:

$P(A)=\frac{2\cdot \frac{1}{2}\cdot\left(\frac{3}{4}\right)^2}{1}=\frac{9}{16}$


Посчитать площадь B ещё проще. Оно занимает семь квадратов в общем пространстве элементарных событий, состоящем из 16 квадратов:

$P(B)=\frac{7}{16} $


Расчёт пересечения

Теперь, когда известны площади A и B, изобразим их пересечение:


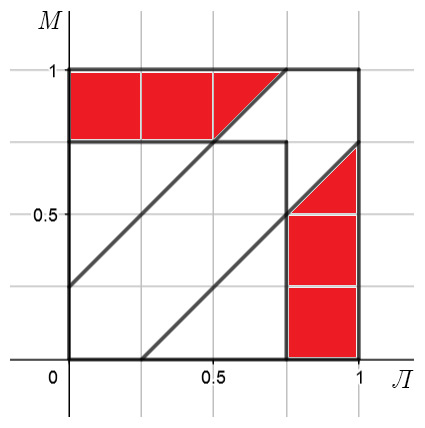
Стало видно, что они занимают 5 квадратов:

$P(A \cap B)=\frac{5}{16}$


В начале разбора мы выяснили, что для независимости A и B должно выполниться условие:

$P(A \cap B)= P(A)\cdot P(B)$


Однако:

$P(A \cap B)=\frac{5}{16},P(A)=\frac{9}{16},P(B)=\frac{7}{16},$

$P(A \cap B) \neq P(A)\cdot P(B)$


Следовательно, события А и B не независимы.

Ответ: нет, события не независимы.