Те, кто увлекается ретрокомпьютингом в области самостоятельной сборки компьютеров на базе 8-битных процессоров (i8080/i8085/z80/z180/6502/6809 и т.п.) или микроконтроллеров, обычно сталкиваются с необходимостью отображения в процессе отладки и/или "эксплуатации" какой-либо информации (содержимого шин адреса, данных и др.) на 7-сегментных индикаторах в шестнадцатеричном представлении.

В принципе, задача отображения шестнадцатеричных разрядов с лёгкостью решается необходимым количеством «умных» индикаторов TIL311. Эти хорошо известные индикаторы, разработанные компанией Texas Instruments задолго до того, как вымерли динозавры, ещё производятся и их можно найти на Aliexpress.

Несмотря на удобство использования, эти индикаторы имеют и существенные недостатки, а именно:

• Относительная дороговизна — даже на Aliexpress эти индикаторы стоят совсем не дёшево (по сравнению с обычными 7-сегментными индикаторами) и их не станешь покупать впрок по принципу «авось пригодятся»;

• Отсутствие в шаговой доступности — их надо специально заказывать и ждать, т.е. совсем не тот случай, когда нужно что-то смакетировать на быструю руку;

• Они существуют только в красном свечении — не самый важный недостаток, но иногда может иметь существенное значение.

Для увлечений в области ретрокомпьютинга дешёвой и доступной альтернативой является использование обычных, везде и всюду распространённых, 7-сегментных LED-индикаторов любого цвета и размера с дополнительным дешифратором. На роль компактного дешифратора лучше всего, конечно, подходят простые микросхемы программируемой логики (напр. GAL16V8) — эти микросхемы всё ещё распространены, достаточно дёшевы и в силу своей простоты (и при этом гибкости) необычайно полезны, что является достаточным основанием для того, чтобы иметь их в хозяйстве хотя бы десяток.

Использование одной микросхемы GAL16V8 в качестве дешифратора одного цифрового 16-ричного разряда мне показалось слишком расточительным избыточным, поэтому пришлось спроектировать логику дешифратора сразу двух 16-ричных разрядов на одной микросхеме GAL16V8 (готовых решений подобного типа в сети я не нашёл).

- [В комментариях мне справедливо указали на то, что в качестве дешифратора одной цифры подошли бы и дешёвые программируемые ПЗУ К155РЕ3 (аналог SN74188N). С моей точки зрения, использование этих ПЗУ в домашней любительской практике имеет смысл только в одном случае - если они УЖЕ есть в наличии (т.е. их не надо покупать) и их очень хочется куда-нибудь пристроить. При практически равной стоимости двух К155РЕ3 одному GAL16V8, они займут почти в 2 раза больше места на плате. Не говоря уж о том, что GAL-ы потом, если что, можно повторно использовать в любых других целях, а эти ПЗУ - мало как иначе. Ну а для тех, кому инженерная задача минимизации количества корпусов/выводов на плате представляется не имеющей самостоятельной ценности, существует не менее увлекательная возможность построения дешифратора на дискретных элементах.] -

Часть 1: А так можно?

Составим функциональную таблицу соответствия активных/неактивных сегментов стандартного 7-сегментного LED-индикатора соответствующим значениям отображаемых нибблов — колонке A в таблице соответствует самый старший разряд ниббла, колонке D соответствует самый младший разряд ниббла, активные сегменты индикатора залиты зелёным, неактивные — жёлтым. 

Фактически, таким образом мы задали таблицы истинности семи (по числу сегментов индикатора) разных булевых функций, зависящих от 4-х аргументов — ?(A,B,C,D):

Проведём минимизацию каждой булевой функции с использованием карт Карно для четырёх аргументов. Скриншоты ниже сделаны из файла MS Excel, соответственно для обозначения «склеиваемых» термов я использовал не только различные цвета, но и различные виды границ ячеек (без учёта обычной тонкой сплошной границы).

Так, например, для сегмента a склеиваемые по единицам термы могут иметь 3 цвета (салатовый, зелёный и болотный) и 4 вида границы (двойную '===', сплошную толстую '---',  прерывистую '???' и штрих-пунктирную '?•?•').

Справа от карты Карно каждого сегмента отображён результат минимизации, т.е. минимальная дизъюнктивная нормальная форма (ДНФ) булевой функции соответствующего сегмента. Минимизированные термы сложены вертикально, с отображением той группировки (цвета или границы), по которой производилась минимизация. [Все картинки в статье открывабельны в полном разрешении в отдельном окне/вкладке браузера правой кнопкой мыши]

Здесь и далее в выражениях ДНФ используются следующие обозначения:

a-g — булевы функции четырёх переменных F(A,B,C,D),
*  — операция логического 'И' (логическое умножение, конъюнкция),
+ — операция логического 'ИЛИ' (логическое сложение, дизъюнкция), 
\ — операция логического 'НЕ' (логическое отрицание)

Остальные сегменты (и не только) под спойлером - предлагаю заглянуть ;)

Отмечу, что для понимания этой части статьи крайне желательно разобраться в сути минимизации (хоть с использованием карт Карно, хоть аналитическими методами). Предлагаю интересующимся не верить мне на слово и самостоятельно получить результат хотя бы для одного сегмента.

Эти результаты хорошо и многократно описаны в сети и позволяют легко реализовать на GAL16V8 управление одним 7-сегментным индикатором. Однако управлять двумя 7-сегментными индикаторами одной микросхемой GAL16V8 эти результаты не помогут. Почему?

Если ответ на вопрос «почему с помощью этих функций нельзя управлять двумя индикаторами одним GAL16V8?» понятен, то можно листать вниз до 2-ой части, где я рассказываю как надо сделать, чтобы было можно. А сейчас чуть подробнее о том, почему это нельзя.

Зачем нужна минимизация?

Для начала выясним — а зачем вообще нужна вся эта суета с картами Карно и минимизацией булевых функций?

Вернёмся к исходной таблице соответствия активности сегментов индикатора отображаемым шестнадцатеричным цифрам. Для примера рассмотрим колонку сегмента 'e'.
Видно, что этот сегмент должен загораться в 10 случаях из 16-ти — когда на входе цифра 0 или 2 или 6 или 8 или A или B или C или D или E или F.

Если в двоичном коде, то это 0000 или 0010 или 0110 или 1000 или 1010 или 1011 или 1100 или 1101 или 1110 или 1111.

Ну а в виде булевой функции то же самое очевидным образом выглядит как

e(A, B, C, D) = \A*\B*\C*\D + \A*\B*C*\D + \A*B*C*\D + A*\B*\C*\D +
A*\B*C*\D + A*\B*C*D + A*B*\C*\D + A*B*\C*D + A*B*C*\D + A*B*C*D

Логические слагаемые (т.е. выражения, связанные операцией ИЛИ) в булевой функции называются термами.  Переменные в терме связаны операцией И. Такая форма записи булевых функций называется дизъюнктивной нормальной формой (ДНФ). Вспомним (см. спойлер выше), что после минимизации та же самая булева функция содержит уже не 10, а всего 4 терма:

e(A, B, C, D) = \B*\D + C*\D +  A*B + A*C*D

Посмотрим теперь как устроены микросхемы программируемой логики на примере гипотетической микросхемы GAL4V1 (в обозначении, как и у всамделишных GAL-ов, первое число обозначает максимально возможное число входов, второе — максимально возможное количество выходов): 

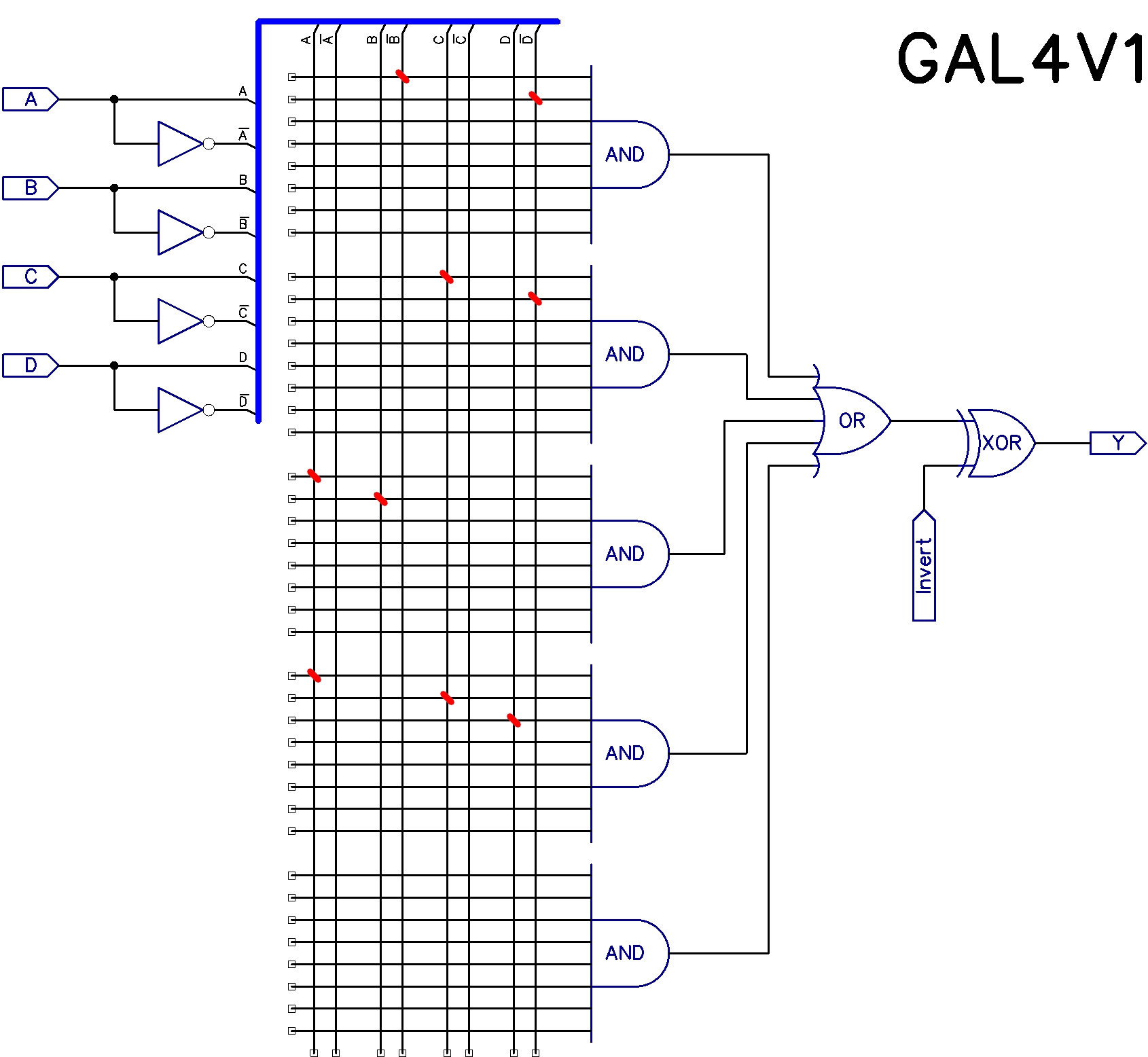
Микросхема GAL4V1 состоит из:

• входного каскада, формирующего с помощью инверторов для каждого входного сигнала 'X' его логическое отрицание '\X';

• матрицы программируемых перемычек, позволяющих формировать термы (максимум 5 термов) из любых комбинаций входных сигналов, соединённых операцией 'И';

• дизъюнктора, объединяющего полученные термы операцией 'ИЛИ';

• выходного каскада, позволяющего с помощью программируемого инвертора на базе элемента 'Исключающее ИЛИ' (eXclusive OR - XOR) формировать прямой или инвертированный результат.

Очевидно, что с точки зрения схемотехники эта микросхема предлагает реализацию булевых функций, представленных в дизъюнктивных нормальных формах. Красные перемычки показывают, что эта микросхема уже кем-то запрограммирована на реализацию ДНФ рассматриваемой нами булевой функции e (A, B, C, D) в её минимизированном варианте (см. спойлер выше).

Любые ли булевы функции, заданные в ДНФ, можно реализовать микросхемой GAL4V1? Глядя на количество входов (4), выходов (1) и на количество объединяемых дизъюнктором термов (5), можно сформулировать правильный ответ — любую одну, при условии, что функция зависит не более чем от 4-х переменных и количество термов в ДНФ функции не превышает 5-и.

Не будь дизъюнктивная нормальная форма функции e(A, B, C, D) предварительно минимизирована, «засувать» её в эту микросхему не получилось бы, а булеву функцию сегмента 'a' на этой микросхеме не реализовать даже в её минимальной ДНФ (7 термов).
Впрочем, не стоит пока торопиться с окончательными выводами... 

А вот вопрос о необходимости минимизации ДНФ полагаю можно считать закрытым ))

Немного о реальных GAL-ах

Сильно ли отличаются всамделишные GAL-ы от рассмотренного гипотетического GAL4V1? С точки зрения способа реализации булевых функций — отличий нет, но реальные GAL-ы имеют дополнительные возможности и/или особенности:

• Больше максимальное количество выходов, т.е. булевых функций, которые может реализовать микросхема (до 8 выходов у GAL16V8 и GAL20V8, до 10 выходов у GAL18V10 и GAL22V10, до 12 выходов у GAL26V12 и GAL26CV12);

• Большее количество термов на каждый выход (7-8 у GAL16V8 и GAL20V8, 8-10 у GAL18V10, 8-16 у GAL22V10 и GAL26V12, 8-12 у GAL26CV12);

• Больше максимальное количество входов, т.е. независимых переменных, из которых можно формировать термы или использовать в других целях (до 16 у GAL16V8, до 18 у GAL18V10, до 20 у GAL20V8, до 22 у GAL22V10 и до 26 у GAL26V12 и GAL26СV12);

• Возможность программирования некоторых (или всех) выходов на работу в режимах «только выход», «выход-вход» или «вход» (таким способом за счёт ненужных выходов увеличивается количество входов);

• Возможность перевода выводов в состояние высокого импеданса.

Принципиальным же отличием реальных микросхем GAL является наличие у каждого выхода 1-битного регистра памяти (D-триггера), которые можно активировать/деактивировать индивидуально для каждого выхода в определённом режиме (GAL16V8 и GAL20V8) или без каких-либо особых режимов (GAL18V10, GAL22V10 и GAL26V12/GAL26CV12). 

Наличие памяти позволяет на основе GAL-ов реализовывать не только простые комбинационные схемы, но и достаточно сложные устройства, основанные на использовании конечных автоматов.

Совокупность 1-битного регистра, дизъюнктора и коммутационной логики выходного каскада называется у GAL-ов "макроячейкой выходной логики" (OLMC — Output Logic MacroCell).

Опять GAL4V1

Пусть на выходе Y необходимо отображать состояние входа A (т.е. просто сделать повторитель сигнала). Булева функция тривиальна и содержит 1 терм:

Теперь пусть на выходе Y необходимо отображать состояние входа A только в том случае, если на разрешающем входе B присутствует сигнал низкого уровня:

Эта функция хоть и зависит теперь от 2-х переменных, но всё ещё содержит 1 терм.

Чуть усложним задачу — пусть на выходе Y необходимо отображать состояние входа A в том и только в том случае, если на разрешающем входе B присутствует разрешающий сигнал высокого уровня, а на разрешающем входе C сигнал низкого уровня:

Добавилась ещё одна переменная, от которой зависит значение функции, но количество термов не изменилось.

А вот теперь попробуем мультиплексировать входные сигналы на один и тот же выход: если на управляющем входе C логический ноль, то необходимо на выход Y передавать информацию со входа A, а если на входе C логическая единица, то на выход Y передавать информацию со входа B:

Получился простейший мультиплексор сигналов. Булева функция также зависит от 3-х переменных, но для нас здесь важно то, что мультиплексирование двух сигналов требует в 2 (два) раза больше термов, чем передача одного сигнала. Почему? А потому, что появилась альтернатива ИЛИ — «или этот вариант или тот».

Зачем мультиплексировать?

Для управления (включения/выключения) каждого сегмента 7-сегментного индикатора требуется отдельный выход дешифратора. Для управления двумя индикаторами без использования мультиплексирования потребовалось бы 7+7=14 управляющих выходов (а если нужно использовать и индикаторы точек, разделяющих разряды, то и все 16). 

Мало того, что такого количества выходов не имеет ни одна из упомянутых ранее микросхем GAL, но и сам такой экстенсивный подход является неэффективным с точки зрения расходования ресурсов.

Поэтому, если и существует способ построения дешифратора 2-х 7-сегментных индикаторов на одной микросхеме программируемой логики, то либо эта микросхема должна иметь много выходов, либо необходимо эффективно использовать малое количество имеющихся — например применять разделенное по времени (т.е. мультиплексированное) использование одних и тех же выходов дешифратора для поочерёдного управления обоими индикаторами.

А что же GAL16V8?

Даташит на GAL16V8 объясняет, что все макроячейки выходной логики (т.е. совокупность дизъюнктора, 1-битного регистра памяти и коммутационной логики на каждом выходе) могут работать в 3-х разных режимах, т.н. Registered, Complex и Simple. Опуская несущественные здесь детали, разницу между ними можно описать следующим образом.

В режиме Simple каждый выход (а их может быть 8) аналогичен рассмотренной ранее гипотетической GAL4V1, но дизъюнктор каждого выхода объединяет уже 8 термов и количество входных переменных — не менее 10. Возможность перевода выходов в состояние высокого импеданса в этом режиме отсутствует.

В режиме Complex выходы работают подобно режиму Simple, но появляется возможность переводить их в состояние высокого импеданса сигналом Output Enable (\OE), формируемым с помощью отдельного терма. По этой причине общее количество "пользовательских" термов на каждом дизъюнкторе не может превышать 7 термов. Количество независимых входных переменных — не менее 10.

В режиме Registered на каждом (любом или всех сразу) выходе между программируемым XOR-инвертором и выходным буфером активируется 1-битный синхронный регистр (D-триггер), запоминающий состояние выходного сигнала по фронту сигнала CLK, общему для всех триггеров и подаваемому на выделенный в этом режиме контакт 1 микросхемы. Есть возможность переводить регистровые выходы в состояние высокого импеданса сигналом \OE, подаваемым на выделенный в этом режиме контакт 11 микросхемы. Максимальное количество термов на регистровых дизъюнкторах — 8. Если выход не использует регистр, то работает подобно режиму Complex и имеет не более 7 термов. Количество независимых входных переменных — не менее 8.

И какой из этого вывод?

Любой из этих режимов позволяет построить на GAL16V8 дешифратор одной шестнадцатеричной цифры, т.к. количество термов в булевых функциях сегментов находится в пределах от 4 (сегмент 'e') до 7 (сегмент 'a') и не превышает возможностей любого из режимов.

Возвращаясь к теме данной статьи, т.е. к управлению двумя 7-сегментными индикаторами одним GAL16V8, становится понятным, что если для декодирования и отображения одной шестнадцатеричной цифры может потребоваться до 7 термов (в случае сегмента 'a'), то для декодирования и отображения двух шестнадцатеричных цифр в режиме мультиплексирования потребуется в 2 раза больше термов.

Собственно, на этом можно закончить разъяснение того, почему с помощью даже минимизированных ДНФ булевых функций, описанных в начале статьи и реализующих дешифратор одного 7-сегментного индикатора, нельзя построить дешифратор двух 7-сегментных индикаторов на одной микросхеме GAL16V8.

Оставшаяся часть статьи объясняет как можно построить дешифратор двух 7-сегментных индикаторов на одной микросхеме GAL16V8. 

Часть 2: Вот так - можно!

Для заявленной в названии статьи цели (т.е. для дешифрации двух шестнадцатеричных цифр) нас интересуют режимы с максимально возможным количеством термов на дизъюнкторе каждого выхода, т.е. режимы Simple и Registered, имеющие по 8 термов на каждый выход. 

Стало быть, как уже выяснено в предыдущем разделе, для использования GAL16V8 для дешифрации двух 16-ричных цифр в режиме мультиплексирования выходов любая минимизированная дизъюнктивная нормальная форма булевой функции должна состоять не более чем из 4-х термов. Как этого добиться? 

Вспомним, что в начале 1-ой части статьи минимизация ДНФ производилась по единицам, т.е. по тем входным термам, значение которых дает логическую единицу на выходе сегмента.

Что, если зайти от обратного и провести минимизацию по нулям? Ведь если мы знаем, что для нескольких наборов значений входных переменных булева функция принимает значение логического нуля, то это означает, для для всех остальных значений на входе (уже неважно каких) булева функция принимает значение логической единицы, что нам и надо. 

Говоря другими словами, если мы применим операцию логического отрицания к булевой функции, принимающей значение «истина» на тех входных термах, которые должны «гасить» сегмент, то в результате получим искомые единицы.

Проведём минимизацию обратных функций каждого сегмента с помощью тех же карт Карно. Для обозначения «склеиваемых» термов по нулям я использовал уже не различные цвета и типы границ, а выделение жирным и два вида перечёркивания ячеек ('\' и '/'). Одиночные, ни с кем не «склеиваемые» нули я никак не выделял : 

Остальные сегменты под спойлером

Как видно, количество термов в любой из 7-ми обратных функций \a(A,B,C,D), \b(A,B,C,D), ..., \g(A,B,C,D) не превышает 4-х, что нам и требовалось!

Кстати, обратите внимание, что в таком виде любая их этих функций могла бы быть реализована силами GAL4V1, да ещё и с запасом ;)

Пора проверить результат на практике.

Программируем GAL16V8D

В качестве иллюстрации к этой статье нарисовал простую схему — набираем любые 2 шестнадцатеричные цифры в двоичном коде на DIP-переключателе и тут же видим эти цифры на индикаторе:

Простейший генератор похожего на меандр прямоугольного сигнала (особая точность здесь не нужна) для управления мультиплексором — на любом 555 (КР1006ВИ1 / NE555 / LM555 / LMC555 / SA555 / TLC555 / итп). Частота "меандра" в данном случае выбрана 200Гц, но может быть и иной - главное, чтобы переключение разрядов индикатора было незаметно для глаз. Более важна здесь скважность, которая для меандра равна 2.

Транзисторы работают в режиме ключа — подойдут любые PNP с допустимым током коллектора не менее 100 мА. Индикаторы — любые 7-сегментные с общим анодом. Тут необходимо сделать пояснение.

Как мы помним, наши обратные булевы функции принимают значение единицы для тех входных термов, которые должны «гасить» сегменты и нуля для тех, которые должны их «зажигать». 

Можно было бы задействовать XOR-инверторы выходных каскадов GAL16V8 и выдавать единицы на LED-индикаторы с общим катодом, но выходные буферы GAL16V8D имеют небольшую нагрузочную способность по току логической единицы, зато более чем достаточную по току логического нуля:

Вроде как существовали GAL16VP8 с мощными выходными буферами-драйверами (до 64 мА на каждый выход), но мне такие не попадались. Поэтому логичным был выбор в пользу индикаторов с общим анодом (я использовал такой).

До установки 2-значного LED-индикатора собранная на короткой макетке схема выглядела вот так (для генератора 200Гц-меандра не хватило всего 4-х рядов, пришлось размещать на отдельной макетке):

Монтажная схема отличается от принципиальной лишь подключением анодов сдвоенного индикатора 5261BS - для удобства монтажа, из-за особенности его цоколёвки, на макетной плате анод старшего разряда подключен к сигналу EN_L, а анод младшего - к EN_H.

Код конфигурации GAL16V8D для этой монтажной схемы (код конфигурации, соответствующий принципиальной схеме, отличается только полярностью сигналов EN_H/EN_L) набирался и компилировался в WinCUPL (это ПО вместе с кодом активации бесплатно доступно на сайте компании MicroChip), поэтому и синтаксис соответствующий (& - операция логического 'И', # - операция логического 'ИЛИ', ! - операция логического 'НЕ'):

Можно убедиться, что все булевы функции сегментов в конфигурации полностью соответствуют ранее выведенным булевым функциям для нулей. Я постарался добавить комментарии (к сожалению, кириллицу WinCUPL не всегда любит), поэтому хочется думать что после прочтения всего предыдущего текста код должен быть очевидным...

Ну, разве что стоит наверное дополнительно сказать о сигнале EN_L и почему он в разделе выходных, а не входных сигналов. На самом деле он может быть и входным, но в данном случае он выходной-входной. 

Тут дело в следующем — в связи с тем, что используется режим динамической индикации (т.е. когда цифры светятся поочерёдно, в свои определённые промежутки времени), то в общем случае, когда цифр может быть больше 2-х, для указания периода свечения (и декодирования) конкретной цифры сигнал EN_i должен быть таким же прямоугольным входным сигналом требуемой скважности, как и EN_j, но с другой фазой :

В данном же конкретном случае, когда цифр только две (или когда мультиплексируются чётные/нечётные разряды) и они декодируются/светятся поочерёдно, можно генерировать второй меандр для EN_L из меандра EN_H в противофазе силами самого GAL16V8, что и делается оператором «EN_L  =  ! EN_H» : 

Сигнал EN_L, таким образом, формируется как выходящий (для управления транзисторным ключом младшей цифры) и тут же используется как входящий (при формировании флагов LED1/LED2 управления мультиплексором). 

Для прошивки в GAL16V8D JED-файла конфигурации (получившегося в результате компиляции исходного кода) использовался широкоизвестный программатор MiniPro TL866A. Сама процедура прошивки занимает не более 5 секунд :

Ну и да — разумеется, всё работает так, как и должно — один GAL16V8 работает дешифратором для двух 7-сегментных индикаторов:

В процессе создания этой статьи я наткнулся на хорошую публикацию на Хабре - PAL, GAL и путешествие в цифровое ретро / Хабр (habr.com) и подумал, что мой кейс может быть интересен тем, кто не считает, что булки растут в магазине, вода возникает из крана, а электричество из розетки и хочет понять из чего всё выросло и самостоятельно разобраться в основах цифровой логики на простом, но не тривиальном примере.

P.S. Таблица MS Excel с картами Карно и минимизированными булевыми функция, исходный код конфигурации GAL16V8D и JED-файл для прошивки лежат здесь.
P.P.S. Все фото и иллюстрации в данной статье - мои.