Модель прогнозирования временных рядов по выборке максимального подобия: пояснение и пример / forpes.ru

Главная
Модель прогнозирования временных рядов по выборке максимального подобия: пояснение и пример

Модель прогнозирования временных рядов по выборке максимального подобия: пояснение и пример +14

17.09.2015 07:49

mbureau 16 5779 Источник

Предисловие

Это моя модель. Я ее придумала, программно реализовала, изучила особенности и описала. Полученное описание защитила как диссертацию по теме «Модель прогнозирования временных рядов по выборке максимального подобия». Разработанная модель относится к классу статистических моделей прогнозирования и строит прогноз временного ряда на основании фактических значений того же ряда. Подробнее о классификации я писала ранее. Одна из модификаций модели позволяет учитывать влияние внешних факторов на прогноз.

Файлы с реализованным примером можно скачать в архиве.

1. Пояснение модели прогнозирования по выборке максимального подобия

1.1. Основная идея и ее иллюстрация на выборках временного ряда

Полное формальное описание модели прогнозирования можно найти во второй главе моей диссертации. Однако если говорить просто, то в основу модели положена идея о развитии истории по спирали: этапы повторяются, но с изменяющимися свойствами.

Если приложить указанную идею к временным рядам, то можно сказать так: в фактических значениях временного ряда, если их достаточно много, наверняка есть отрезок, который очень похож на то, что происходит накануне прогноза.

На рис. 1 представлена часть временного ряда Z(t), для которого без специальных вычислений заметны похожие отрезки. Назовем отрезок временного ряда, имеющий начало в отметке времени tи длину (число отсчетов) M, выборкой временного ряда (time series pattern) и обозначим Z^M_t.

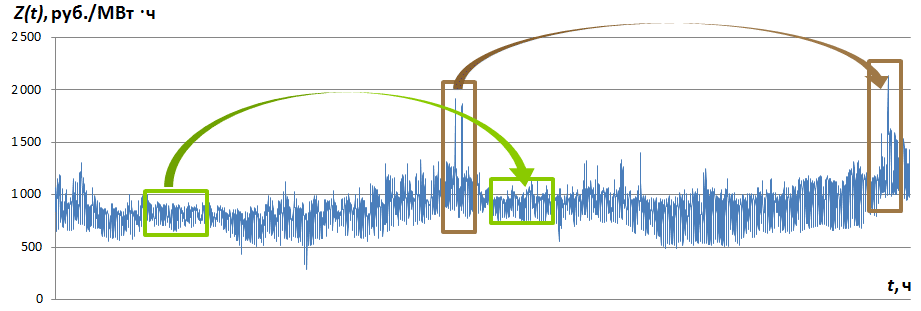
Рис. 1. Временной ряд Z(t)и некоторые его выборки

Всякая модель прогнозирования исходит из некоторого предположения. В модели по выборке максимального подобия предполагается, что если история повторяется, то для каждой выборки, предшествующей прогнозу, есть подобная выборка, содержащаяся в фактических значениях этого же временного ряда. Формально это называется гипотеза подобия (см. диссертацию).

Соотношение выборок и их название можно увидеть на рис. 2.

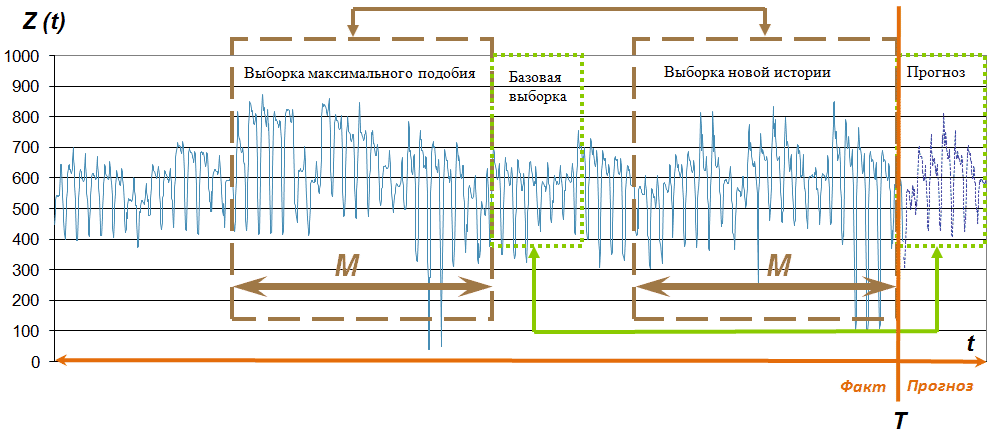
Рис. 2. Выборки временного ряда Z(t)

В момент времени T, который называется моментом прогноза, нужно определить Pзначений временного ряда в будущем, т. е. вычислить выборку Прогноз. При этом значения Выборки новой истории являются доступными. Далее, исходя из предположения о том, что для каждой выборки есть подобная, нужно найти Выборку максимального подобия для Выборки новой истории и предположить, что история повторится, то есть основой для прогнозных значений станет Базовая выборка.

Далее необходимо ответить на три вопроса.

1.2. Как определить подобие выборок?

В своей диссертации я предлагаю самый простой вариант определения подобия — вычисление значения линейной корреляции. Берем одну выборку длины M, берем другую выборку длины M, считаем значение корреляции, которое и будет отражать подобие двух выборок.

Искать Выборку максимального подобия проще всего методом перебора среди всех возможных выборок. Для временных рядов до 100 000 значений такого сорта перебор занимает несколько секунд при реализации на персональном компьютере средней мощности.

Предложенный подход определения подобия не является единственно возможным. Ряд студентов-последователей предлагали в своих работах иные методы определения подобия двух выборок. Вы можете применить здесь вашу фантазию!

1.3. Как «перенести» изменение свойств?

В связи с тем, что в основу определения подобия заложена линейная корреляция, то самым простым вариантом «перенесения» свойств выборок является линейная зависимость

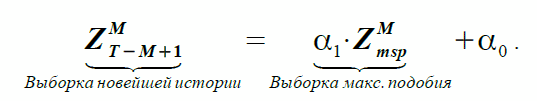Формула 1

(1)

Если уравнение (1) отражает зависимость двух фактических выборок при помощи коэффициентов ?₁ и ?₀, то на основании предположения о подобии Прогноз и Базовая выборка соотносятся следующим образом:

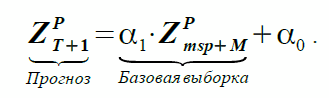Формула 2

(2)

Коэффициенты ?₁ и ?₀ в обоих уравнениях одинаковые, однако для уравнения (1) они являются неизвестными и их нужно определить, а для уравнения (2) они являются известными. Индекс msp расшифровывается как most similar pattern.

Название модели на английском звучит как extrapolation (или forecast) model on the most similar pattern, сокращенно EMMSP.

1.4. Всегда ли работает предположение о подобии?

Это нужно проверять для каждой новой задачи. Всякая модель временного ряда есть инструмент обращения с этим рядом, и, как всякий инструмент, модель нужно использовать должным образом. Грубо говоря, гвозди нужно забивать молотком и землю копать лопатой, а не наоборот.

Разработанная модель показала отличные результаты в задачах краткосрочного прогнозирования временных рядов в области электроэнергетики, где нужно прогнозировать цены и объемы энергопотребления. Модель показала результаты, сравнимые с результатами других моделей прогнозирования, на финансовых временных рядах, уровне сахара крови и др. Численные значения ошибок можно найти в четвертой главе диссертации и наборе отчетов о прогнозировании показателей оптового рынка электроэнергии и мощности.

Самое важное свойство предложенной модели — ее простота и наглядность.

2. Пример реализации модели прогнозирования по выборке максимального подобия в MATLAB

Пример модели прогнозирования реализован в MATLAB.

2.1. Исходные данные, постановка задачи прогнозирования и параметры модели

Исходными данными являются значения цен на электроэнергию европейской территории РФ оптового рынка электроэнергии и мощности в руб./МВт•ч с 01.09.2006 до 13.11.2012 в почасовом разрешении. Архив PRICES_EUR содержит 54 384 значения.

Необходимо вычислить прогноз данного временного ряда на P=24 значения вперед, т. е. на сутки вперед в момент прогноза T = 01.09.2012 23:00:00.

Загрузка исходных данных:

% Цены рынка на сутки вперед оптового рынка электроэнергии и мощности
% в почасовом разрешении, матрица PRICES_EUR имеет три столбца
% <Date> - <Hour> - <Value>
load PRICES_EUR PRICES_EUR;         % Загрузка исходных данных из файла PRICES_EUR.mat
TimeSeries = PRICES_EUR;

Постановка задачи прогнозирования:

% Постановка задачи прогнозирования
T = datenum('01.09.2012 23:00:00', 'dd.mm.yyyy hh:MM:ss'); 	% Момент прогноза (Origin)
P = 24;                                                     			% Горизонт прогнозирования (Forecast horizon)

Параметры модели прогнозирования EMMSP:

% Параметры модели по выборке максимального подобия
M = 144;
Step = 24;

В данном случае длина Выборки новой истории и Выборки максимального подобия равна M=144. Подробнее о том, как определять M, читайте в третьей главе диссертации.

Переменная Step является шагом перебора фактических значений при определении Выборки максимального подобия.

2.2. Алгоритм модели прогнозирования по выборке максимального подобия

2.2.1. Определить выборку новой истории

Index = find(TimeSeries(:,1) == datenum(year(T), month(T), day(T)) & TimeSeries(:,2) == hour(T));
if length(Index) > 1
    fprintf(['Ошибка временного ряда: отметка времени T найдена во временном ряде более 1 раза \n']);
elseif isempty(Index)
    fprintf(['Ошибка временного ряда: отметка времени T во временном ряде не найдена \n']);
else
    HistNewData = TimeSeries([Index-M+1:Index],:);      % Выборка новой истории (HistNewData)
    Index = Index - Step * 2;
end

2.2.2. Определить значения подобия

k = 1;
while Index > 2 * M
    HistOldData = TimeSeries([Index-M+1 : Index],:);
    Likeness(k,1)= Index;
    CheckOld = find(HistOldData(:,3) > 0);                    % Проверка на то, нулевые ли векторы
    CheckNew = find(HistNewData(:,3) > 0);
    if isempty(CheckOld) || isempty(CheckNew)                   
        Likeness(k,2) = 0;
    else
        Likeness(k,2) = abs(corr(HistOldData(:,3), HistNewData(:,3), 'type', 'Pearson'));
    end
    k = k + 1;
    Index = Index - Step;       % Возврат по времени назад на шаг Step
end

Шаг перебора Step = 24 взят из того соображения, что временной ряд имеет ярко выраженную суточную периодичность.

2.2.3. Определить максимум подобия

MaxLikeness = max(abs(Likeness(:,2)));
IndexLikeness = find(Likeness(:,2) == MaxLikeness);
MSP = Likeness(IndexLikeness(1),1);

Практика показывает, что максимумов подобия может быть несколько. Удобнее всего взять первый.

2.2.4. Определить выборку максимального подобия

MSPData = TimeSeries([MSP-M+1 : MSP],:);      % Выборка максимального подобия (MSPData)

2.2.5. Определить базовую выборку

HistBaseData = TimeSeries([MSP+1:MSP+P],:);     % Базовая выборка (HistBaseData)

2.2.6 Поиск коэффициентов ?₁ и ?₀

% Делаем аппроксимацию HistNewData при помощи MSPData по методу наименьших квадратов.
% В данном случае решение находится через обратную матрицу.
% В диссертации решение сделано иным способом, однако матричный метод мне больше нравится.
X = MSPData(:,3);
X(:,length(X(1,:))+1) = 1;      % Добавляем столбец с единичным вектором I
Y = HistNewData(:,3);
E = X(:,2);
Xn = X'* X;
Yn = X'* Y;
invX = inv(Xn);
A = invX * Yn;                  % Искомые коэффициенты alpha1 и alpha0 являются значениями матрицы A

После нахождения значений коэффициентов ?₁ и ?₀ можно сделать проверку, с какой ошибкой Выборка новой истории подобна Выборке максимального подобия, т. е. какова ошибка уравнения (1). В настоящем примере проверка для простоты опущена.

2.2.7. Прогнозирование

X = HistBaseData(:,3);
X(:,length(X(1,:))+1) = 1;
Forecast = X * A;               % Выборка Прогноз, содержащая 24 прогнозных значения

В реализованном примере число прогнозных отсчетов может быть изменено при помощи изменения параметра P.

2.2.8. Оценка ошибки прогнозирования

% 1) Определяем фактические значения
Index = find(TimeSeries(:,1) == datenum(year(T), month(T), day(T)) & TimeSeries(:,2) == hour(T));
Fact = TimeSeries([Index : Index+P-1],3);
 
% 2) Оценка ошибки MAE
MAE = mean(abs(Forecast - Fact));
% 3) Оценка ошибки MAPE
MAPE = mean(abs(Forecast - Fact)./Fact);
 
fprintf(['Момент прогноза T = ',datestr(T,'dd.mm.yyyy HH:MM'),'\n', 'Горизонт прогноза P = ', num2str(P),'\n', 'Ошибка прогноза MAE = ',num2str(MAE),' RUB/MWh, MAPE = ',num2str(MAPE*100),'%% \n']);

По итогам выполнения программы в командной строке MATLAB должно появиться сообщение:

Максимальное подобие MaxLikeness = 0.95817
Коэффициент alpha1 = 1.0312, коэффициент alpha0 = -11.1992
Момент прогноза T = 01.09.2012 23:00
Горизонт прогноза P = 24
Ошибка прогноза MAE = 57.6383 RUB/MWh, MAPE = 6.0065%

Вопросы? Можете задавать их здесь, если у вас есть аккаунт на хабре, или на нашем форуме, если у вас его нет.

Комментарии (16)

Bas1l
17.09.2015 11:34
#8576733
+1
А есть ли у вас статьи в журналах (желательно, международных) или выступления на конференциях (тоже желательно международных)?
1. mbureau
  17.09.2015 11:40
  #8576741
  +3
  Статьи по данной теме у меня есть.
  
  И. Чучуева «Модель экстраполяции по выборке максимального подобия», журнал «Информационные технологии», декабрь 2010.
  
  И. Чучуева, С. Чернецов «Прогнозирование уровня глюкозы в крови больных инсулинозависимым диабетом нейронными сетями и методом экстраполяции по выборке максимального подобия», ноябрь 2010, technomag.edu.ru/doc/162847.html.
  
  И. Чучуева «Модель экстраполяции по максимуму подобия (ЭМП) для временных рядов цен и объемов на рынке на сутки вперед ОРЭМ (Оптовом рынке электроэнергии и мощности)», январь 2010, technomag.edu.ru/doc/135870.html.
  
  И. Чучуева, Ю. Павлов «Экстраполяция псевдослучайных процессов по максимуму подобия», июль 2009, technomag.edu.ru/doc/129712.html.
  
  И. Чучуева «Модель экстраполяции по выборке максимального подобия», июнь 2010, Труды третьей международной конференции «Математическое моделирование социальной и экономической динамики», Москва.
  
  И. Чучуева «Прогнозирование временных рядов при помощи модели экстраполяции по выборке максимального подобия», март 2010, Сборник материалов международной научно-практической конференции «Наука и современность — 2010», Новосибирск.
  
  С международными (на английском) пока все плохо — их нет, но планирую.
  
  Если вы хотите сослаться, то лучше на диссертацию или автореферат.

netmaxed
17.09.2015 13:35
#8576999
а чем Ваш метод отличается от метода «к ближайших соседей» с к=1?
на каких датасетах вы проверяли качество предсказания?
как ваш метод работает на сложных рядах, например usdrub?
1. mbureau
  17.09.2015 13:43
  #8577019
  +1
  Чтобы я могла ответить на этот вопрос, пришлите, пожалуйста, ссылку на внятное описание метода «к ближайших соседей».
  
  В первую очередь, временные ряды из электроэнергетики: цены и энергопотребление. Кроме того, уровень сахара крови и ряд других показателей.
  
  Никак. Ко мне пачками ломятся форексяне, устала уже от них. Я прогнозом на валютных парах не занимаюсь вообще.

netmaxed
17.09.2015 14:16
#8577091
-1
ru.wikipedia.org/wiki/%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_k_%D0%B1%D0%BB%D0%B8%D0%B6%D0%B0%D0%B9%D1%88%D0%B8%D1%85_%D1%81%D0%BE%D1%81%D0%B5%D0%B4%D0%B5%D0%B9

Кроме того, мне не понятно, почему бы не посчитать свертку «выборки новой истории» со всем временным рядом?
Через FFT это будет быстро и эффективно и сразу даст максимум на периоде лучшего совпадения и вам не нужен будет шаг Step.
1. mbureau
  17.09.2015 14:23
  #8577105
  Вот мне нравится :-) Открываю википею и читаю, что «метод k ближайших соседей метрический алгоритм для автоматической классификации объектов», а предлагаемая мною модель решает задачу прогнозирования временного ряда и для классификации не годится. По-моему, очевидно, что это две разные вещи, нет?
  
  Если же говорить о том, как найти похожую выборку, то вариантов у меня было более дюжины, в том числе евклидово расстояние, упомнятое по ссылке: чего только ни считала — очень много вариантов и идеи было, часть из них быстро откинулась, часть долго обрабатывалась. Здесь представлен простейший случай модели, такой, чтобы в нем студент мог за час разобраться. Я потому и пишу, если у вас не работает линейность, то, пожалуйста, изобретайте новые алгоритмы/методы поиска подходящей выборки.

andreymironov
17.09.2015 14:24
#8577107
-2
Хохоу, так вот же такая модель: http://www.youtube.com/playlist?list=PLiAWGmNyTeL8gT3UJWCOUO3WOD5a93sEX (плейлист youtube из 7 видео). И репа на github в описании к видео указана. Правда, написано это когда автор ещё не ахти как писал на плюсах, но «есть можно».
1. mbureau
  17.09.2015 14:37
  #8577127
  -1
  А кто вам сказал, что автор ее не срисовал с моей? Дата видео 2015, а мои статьи аж в 2009 уходят. С меня написано десятки дипломов в разных ВУЗах. А потом нужно понимать, что идея идеей, она не является «официальной» пока не изложена в научном сообществе. Кулибиных по всему миру очень много.
  
  И еще нравится… «ее автор» (название канала и имя комментатора одинаковые)… это вы что ли? Ну так и пишите от себя.
  1. andreymironov
    17.09.2015 14:42
    #8577133
    -3
    К счастью, я — не он. Вы не допускаете существование братьев и сестёр? А на видео запечатлен весь процесс поиска и создания алгоритма, начиная с идеи. Да и алгоритм этот слишком тривиальный, чтобы из-за него сраться. Более того, автор вообще не претендует на авторство столь ничтожной разработки. И вот что ещё 100%: он о ваших статьях и слыхать не слыхивал, и знамо не знал. Вы же не Пифагор! =) Смешно…
  1. Arastas
    18.09.2015 15:18
    #8578635
    А кто вам сказал, что автор ее не срисовал с моей?
    
    Вы, надеюсь, шутите?

mimicria
17.09.2015 18:11
#8577485
Максимальное правдоподобие у меня всегда ассоциировалось с упрощённым Байесом.
1. mbureau
  17.09.2015 19:07
  #8577547
  Есть такой момент в названии. Там именно правдоподобие (likelihood), у меня подобие (similar).

hardex
17.09.2015 23:39
#8577805
+1
Это моя модель. Таких, как она — много, но эта — моя. Моя модель — мой лучший друг. Она — моя жизнь. Я должен научиться владеть ею так же, как я владею своей жизнью. Без меня моя модель бесполезна. Без моей модели бесполезен я.

grekmipt
17.09.2015 23:49
#8577819
+1
Подобная идея настолько общего характера что разумеется приходила в голову почти любому кто начинал работать в теме прогнозирования временных рядов (сам тоже это же пробовал лет так 10 назад в одной задаче — но в моей задаче оно оказалось неработоспособно).

Основная проблема такого подхода в том, что существует бесконечно много способов описания подобия (текущего отрезка данных и исторического кусочка). При этом, не существует универсального метода поиска функции подобия. А линейная корреляция работает лишь на крайне ограниченных примерах из реальной жизни. Более того, если немного покопаться в такой теме как бифуркации, хаотические аттракторы и т.п., то станет понятно, что в массе реальных задач даже чрезвычайно малые (в евклидовом пространстве) отклонения текущего ряда от исторической реализации могут означать принципиально другой прогноз на ближайшую «траекторию» ряда.

Так что статья (да и сам подход) вполне хороша в качестве учебной иллюстрации для тех кто начинает заниматься вопросом прогнозирования рядов, а бОльшего тут ожидать не стоит. Хотя в некоторых редких случаях результат может быть хорошим (там где зависимости очень четкие, и аттракторы данных достаточно слабо хаотические).
Но в любом случае, спасибо за статью — дорогу осилит идущий.
1. mbureau
  18.09.2015 09:35
  #8578061
  Как говорит профессор МГТУ им Баумана А.П. Карпенко, с которым я работала над рукописью диссертации, «нет ничего проще, чем выдумать новый метод, и одновременно нет ничего сложнее, чем доказать его эффективность (в данном случае высокую точность)». Я с самого начала делала модель для рынка электричества, первый ряд с которым работала были цены на электроэнергию. а в итоге фактически все доказательство эффективности построила на рядах из этой области. Да и теперь моя последняя научная публикация касается вопросов электричества, в частности, оптимизации работы ТЭЦ.
  
  Насчет универсальности пока (8 лет вопросом занимаюсь) мнение такое: универсальной модели нет, у всех есть достоинства и недостатки, которые на временных рядах различных характеристик сказываются по-разному. Гнаться за универсальностью в этой области почти невозможно, хотя, может еще лет через 8 у меня переменится мнение.
  
  А что касается учебной иллюстрации, то совершенно верно, для этого материал и писался.
  1. alexandergoncharenko
    24.09.2015 14:13
    #8588701
    Хорошо бы подошли под данный тип задач ssa и la анализы. Хотя, это как у Бокса: все модели неверны, но некоторые — полезны.