В предыдущих туториалах (часть 1, часть 2) мы изучали методы, моделирующие uplift. Это величина, которая оценивает размер влияния на клиента, если мы взаимодействуем с ним. Например, отправляем смс или пуш уведомление. Давайте обсудим: как измерять качество uplift моделей?

Использовать классические метрики качества для оценки обученной модели не получится, так как нет ground truth по каждому объекту выборки или реальных, настоящих значений uplift. Это значит, что если мы предскажем значение, сравнить его будет не с чем. В этом заключается особенность uplift моделирования: нельзя одновременно прокоммуницировать и не прокоммуницировать с клиентом и посмотреть разницу в его реакции. Поэтому все метрики мы будем рассчитывать, так или иначе группируя объекты выборки. Например, рассматривая 10% выборки, 20% и так далее.

Давайте на реальном датасете обучим простую модель, предскажем uplift и посмотрим, какие есть метрики и как они себя ведут. Все примеры кода из статьи есть в ноутбуке. В нем используется питоновская библиотека для uplift моделирования sklift.

Метрики

uplift@k

Самая простая и понятная метрика - размер uplift на топ k процентах выборки.

Например, с помощью обученной uplift модели мы хотим отобрать какое-то количество клиентов, с которыми будем коммуницировать. Пусть бюджет рассчитан на k% клиентов. Тогда нам интересно оценить качество прогноза не на всей тестовой выборке, а только на объектах с наибольшими предсказаниями при отсечении по порогу в k процентов.

Для расчета uplift@k нужно отсортировать выборку по величине предсказанного uplift и посмотреть разницу средних значений таргета Y (в англоязычных статьях использую термин response rate, мы его тоже будем использовать в дальнейшем) в целевой и контрольной группах. Целевая группа - группа, которая получила коммуникацию. Контрольная группа - которая не получила.

Формула uplift@k

Теоретический uplift@k принимает значения от -1 (когда в целевой группе нет реакций Y=1, а в контрольной группе все клиенты имеют реакцию Y=1) и может достигать величины 1 (противоположная ситуация: в целевой группе все клиенты откликнулись: Y=1, в то время как в контрольной - ни одного случая с Y=1).

На практике uplift@k принимает значения от 0 до 1, в зависимости от выбранного значения k, особенностей датасета и качества модели.

Рассчитывать эту метрику можно двумя различными способами: сначала сортировать по предсказанному uplift и далее считать разницу response rate двух групп. Или наоборот, изначально сортировать объекты из контрольной и целевой групп по отдельности.

# y_val - столбец таргета на валидации
# trmnt_val - столбец флага коммуникации на валидации
# uplift_ct - предсказанный uplift методом ClassTransformation на валидации

Тогда метрику uplift@k можно импортировать и посчитать таким образом:

from sklift.metrics import uplift_at_k


# k = 10%
k = 0.1

# strategy='overall' sort by uplift treatment and control together
uplift_overall = uplift_at_k(y_val, uplift_ct, trmnt_val, 
                             strategy='overall', k=k)

# strategy='by_group' sort by uplift treatment and control separately
uplift_bygroup = uplift_at_k(y_val, uplift_ct, trmnt_val, 
                             strategy='by_group', k=k)

print(f"uplift@{k * 100:.0f}%: {uplift_overall:.4f}"
      f"(sort groups by uplift together)")
print(f"uplift@{k * 100:.0f}%: {uplift_bygroup:.4f}"
      f"(sort groups by uplift separately)")

Получим

uplift@10%: 0.1484 (sort groups by uplift together)
uplift@10%: 0.1521 (sort groups by uplift separately)

Uplift by percentile

Бывает так, что со стороны бизнеса не известно значение порога k и хочется посмотреть, как будет вести себя метрика при разных значениях порога k. Такая метрика в литературе [1] упоминается как uplift by decile. Также ее называют uplift by percentile или uplift by bin.

При построении действуем по аналогии с uplift@k:

1. Сортируем по предсказанному значению uplift

2. Делим отсортированные данные на перцентили / децили / бины.

3. В каждом перцентиле отдельно оцениваем uplift как разность между средними значениями целевой переменной в тестовой и контрольной группах.

Стоит отметить, что в большинстве источников [1] [2] аплифт по перцентилям оценивается независимо в каждом перцентиле, но ничего не мешает вам оценить его кумулятивно. 

Результатом этой метрики, как правило, является таблица [3] или ее визуальное представление в виде графика. Давайте также для каждого перцентиля рассчитаем следующие показатели:

• n_treatment - размер целевой (или treatment) группы 

• n_control - размер контрольной (control) группы

• response_rate_treatment - среднее значение таргета целевой группы

• response_rate_control - среднее значение таргета контрольной группы

• uplift = response_rate_treatment - response_rate_control

Дополнительно добавим расчет среднеквадратичного отклонения для каждой метрики (std_treatment, std_control, std_uplift) для того, чтобы оценивать разброс метрики в каждом перцентиле (формулы вы найдете ниже). 

С помощью кода ниже можно рассчитать таблицу uplift by percentile. Кроме метрик по каждому перцентилю в последней строке total расположены итоговые метрики для всей выборки.

from sklift.metrics import uplift_by_percentile


uplift_by_percentile(y_val, uplift_ct, trmnt_val, 
                     strategy='overall', 
                     total=True, std=True, bins=10)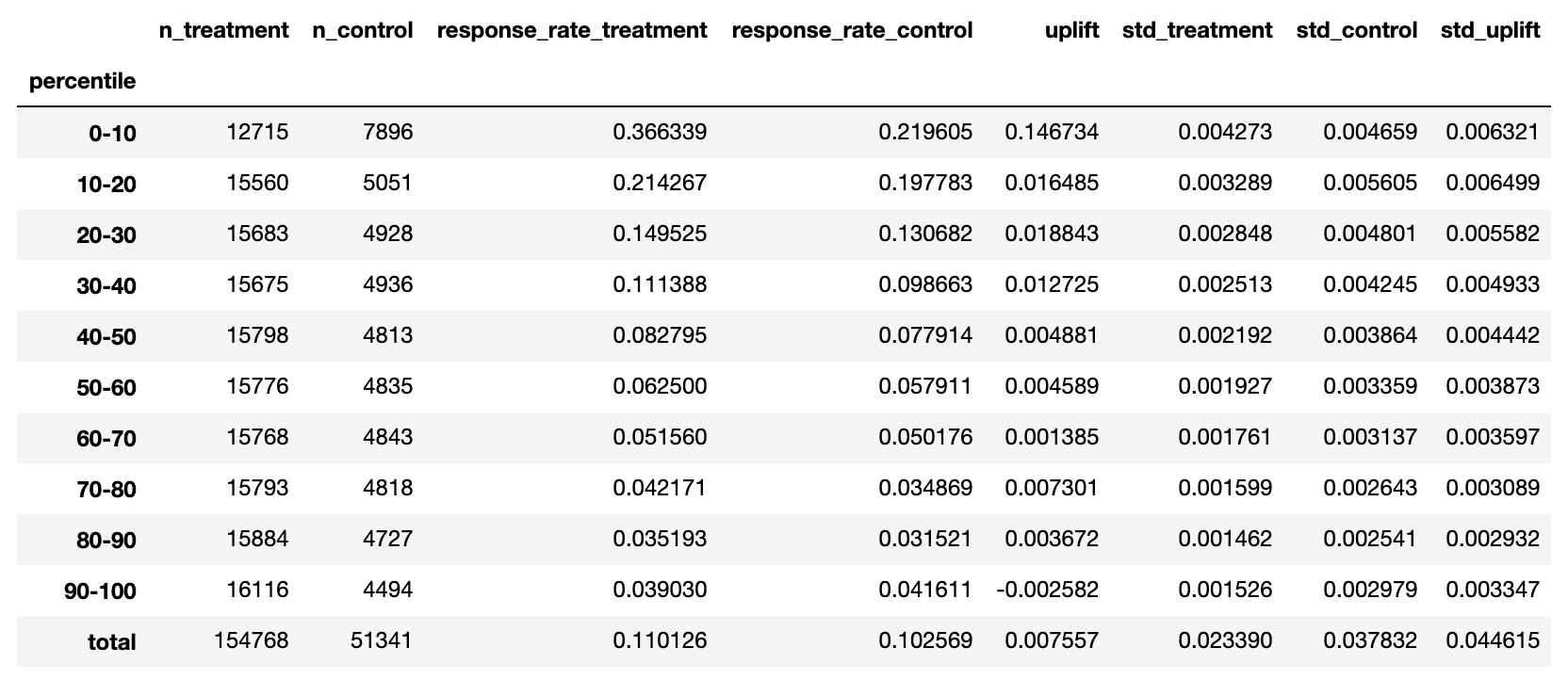

График uplift by percentile

Если визуализировать таблицу, то получится график uplift by percentile. По нему удобно оценивать эффективность модели. Как его можно интерпретировать? Так как коммуникация будет проводиться с клиентами, получившими наибольшую оценку uplift, то слева на графике должны быть максимальные по модулю положительные значения uplift и в следующих перцентилях значения уменьшаются.

Для отрисовки можно использовать bar plot. Для удобства отобразим две графика. На верхнем нарисуем uplift, а на нижнем - соответствующий response rate в тестовой и контрольной группах, разница которых и  является оценкой uplift.

from sklift.viz import plot_uplift_by_percentile


plot_uplift_by_percentile(y_val, uplift_ct, trmnt_val, 
                          strategy='overall', kind='bar');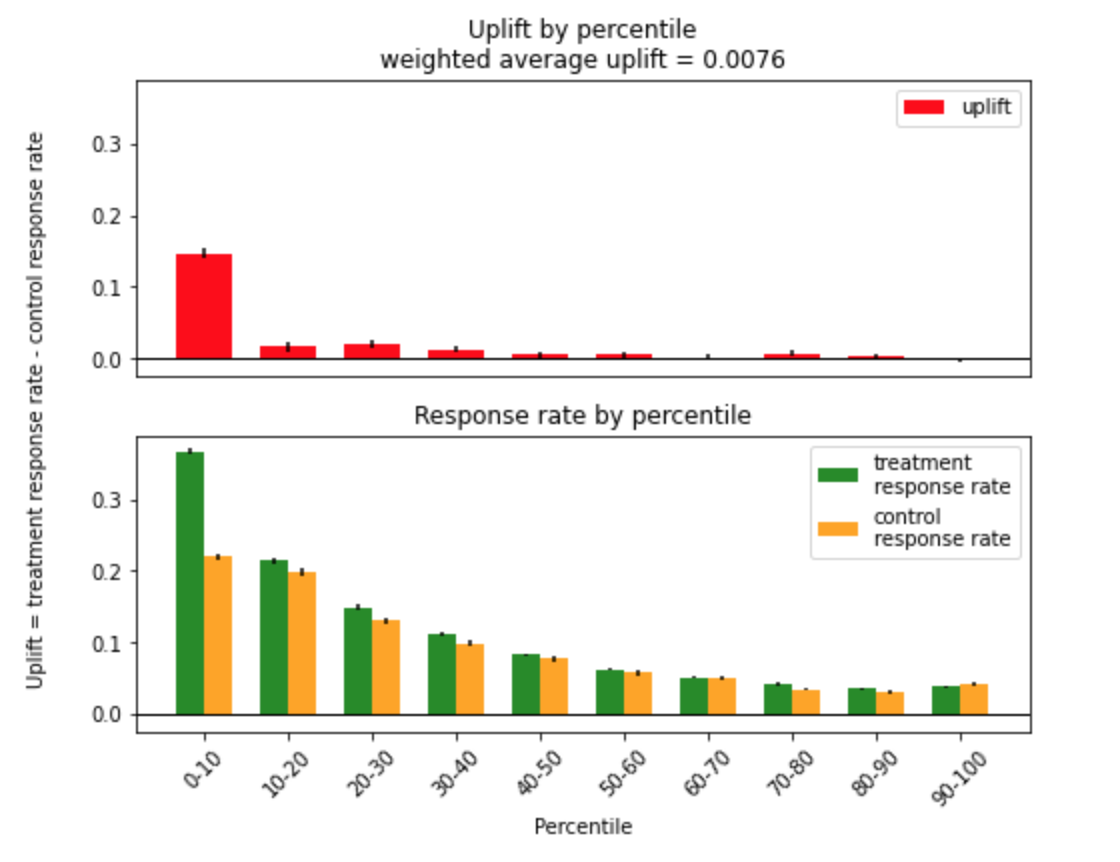

Тогда на графике response rate для целевой и контрольной группы (нижний bar plot) доля реакций клиентов Y = 1 из целевой группы (зеленый цвет) должна быть максимально большой в первых перцентилях и потом убывать. А доля Y = 1 контрольной группы (желтый цвет) - минимальной в первых перцентилях и затем, в идеале, возрастать. Чем больше в первых перцентилях разница двух response rate, тем больше uplift (красный цвет), а значит, тем лучше модель находит клиентов, которые положительно откликаются на коммуникацию.

Если вспомнить разделение по типам клиентов из первого туториала, то в левой части графика как раз находятся убеждаемые - тот тип, которых мы хотим найти. В терминах целевого действия и коммуникации это Y=1 при W=1 или Y=0 при W=0.

На графике могут быть и отрицательные значения uplift. Нетрудно понять, что это случится в том перцентиле, в котором response rate в контрольной группе больше, чем в целевой. Это значит, что коммуникация с этой группой имела негативный эффект и модель нашла тип клиентов, которые негативно реагируют на коммуникацию - тип не беспокоить, Y=0 при W=1, Y=1 при W=0.

Для случайной аплифт модели график uplift by percentile будет выглядеть как линия, параллельная оси Х.

График для идеальной uplift модели выглядел бы так:

На графике между типом убеждаемые в левой части и типом не-беспокоить в правой части лежат два оставшихся типа, которые модель не различает между собой: лояльные и потерянные. Если в выборке их количество будет одинаково, то uplift, равный нулю, должен быть посередине, так как их response rate уравновесит друг друга. Это произойдет потому, что лояльные всегда реагируют и выполняют целевое действие Y=1, а потерянные - наоборот, никогда этого не сделают Y=0. 

Uplift по перцентилям можно визуализировать не только как bar plot, но и как line plot:

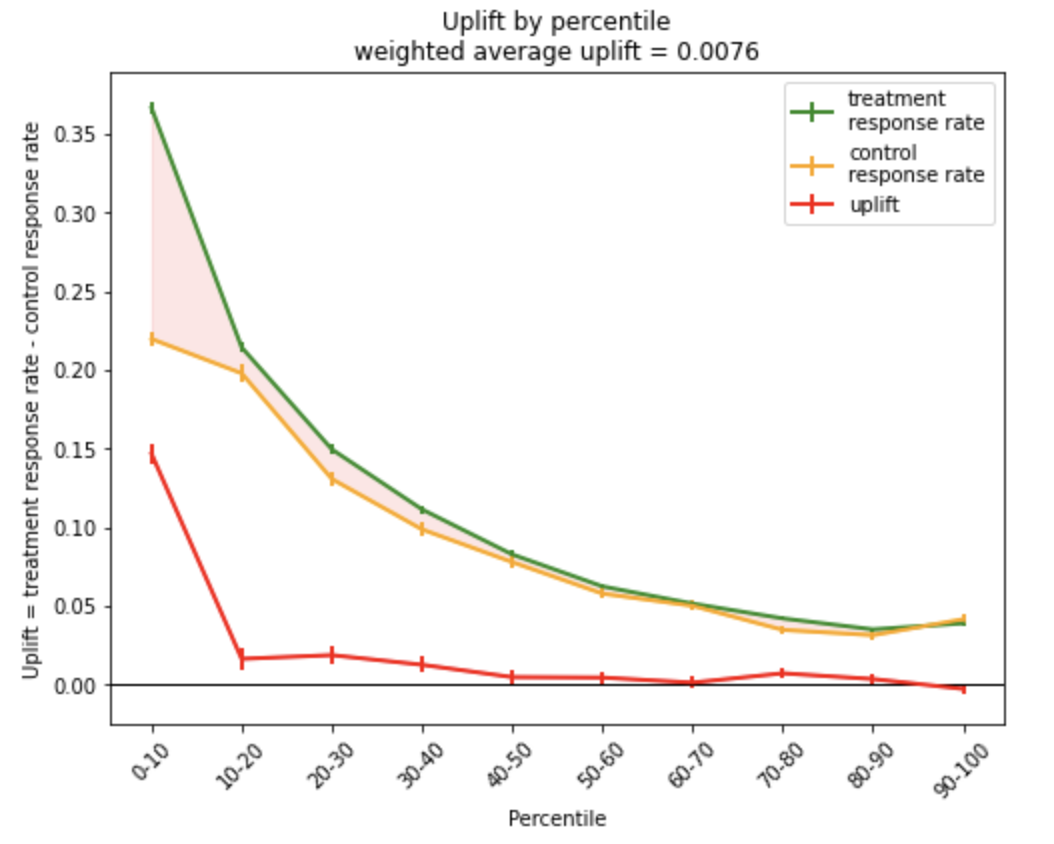
На обоих типах графиков показаны не только  значение uplift в каждой точке, но стандартные отклонения. Это сделано для того, чтобы корректно сравнивать метрики от перцентиля к перцентилю с учетом их разброса.

Выведем формулу стандартного отклонения

По определению 

Чтобы найти стандартное отклонение, вычислим дисперсию и потом возьмем из нее корень:

Так как 

и бинарный таргет распределен по закону Бернулли, получаем

Где

Weighted average uplift

Часто хочется иметь метрику, посчитанную в виде единого значения на всей тестовой выборке. Для этого опять пригодится таблица uplift by percentile. Давайте с помощью значений в столбцах uplift и n_treatment рассчитаем усредненный uplift на всей выборке, взвешенный на размер целевой группы - weighted average uplift [3].

Формула weighted average uplift

from sklift.metrics import weighted_average_uplift


uplift_full_data = weighted_average_uplift(y_val, uplift_ct, 
                                           trmnt_val, bins=10) 
print(f"weighted average uplift on full data: {uplift_full_data:.4f}")

Получим

weighted average uplift on full data: 0.0189

Weighted average uplift лежит в пределах от [-1, 1]и отображается на графике uplift by percentile в названии. Если метрика принимает значение 1, это значит, что реакций Y=1 в контрольной группе нет ни в одном перцентиле: пользователи никогда не выполняют целевое действие самостоятельно, а только при коммуникации. При таком значении метрики нет смысла решать задачу с помощью uplift моделирования, лучше свести постановку задачи к обучению response или look-alike модели.

Значение метрики может доходить до граничного значения  -1. Это будет означать, что во всех перцентилях uplft был равен -1. Такое происходит, когда в целевой группе нет реакций Y=1, а в контрольной группе все клиенты имеют реакцию Y=1. Получается, что значения метрики, которые нас устраивают в рамках решения uplift задачи, лежат в пределах [0, 1).

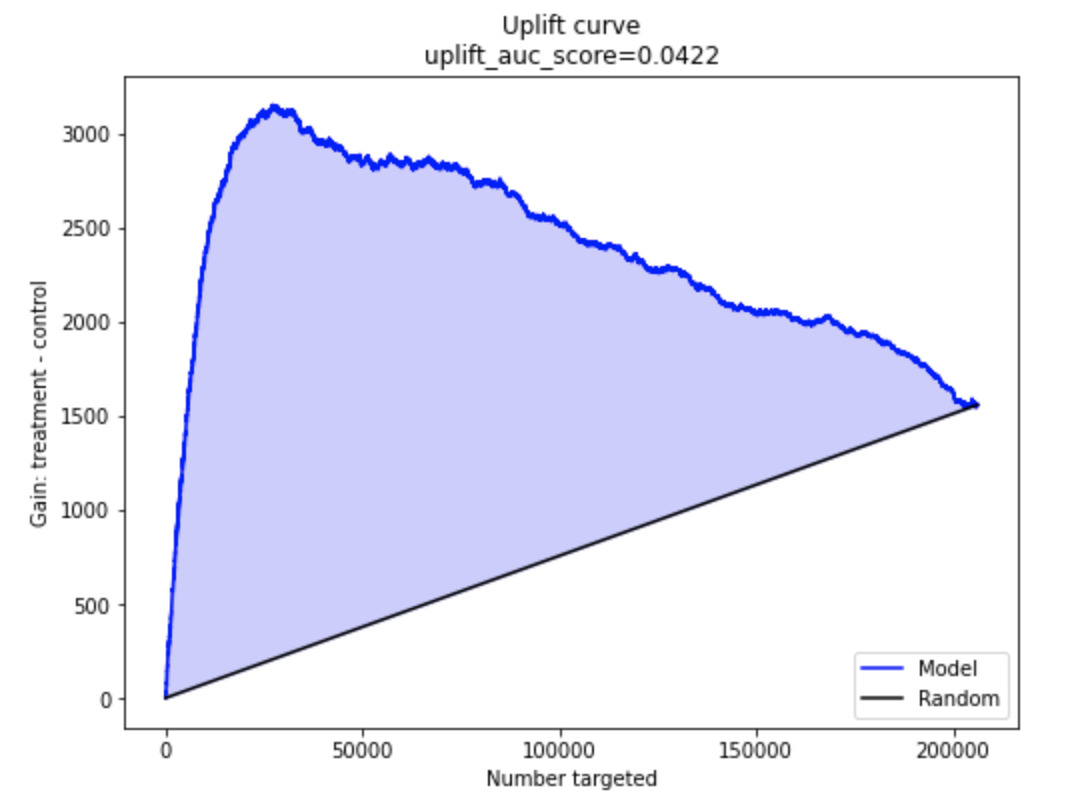
Uplift curve

Uplift кривая строится как функция от количества объектов, нарастающим итогом. В каждой точке кривой можно увидеть накопленный к этому моменту uplift

Формула uplift curve

На картинке ниже расположен типичный график идеальной (красным), модельной, или реальной (синим) и случайной (черным) кривых. Каждая точка на такой кривой соответствует значению кумулятивного uplift. Чем больше это значение, тем лучше. Монотонно возрастающая случайная кривая показывает, что воздействие всей выборки имеет общий положительный эффект. 

from sklift.viz import plot_uplift_curve


# with ideal curve
# perfect=True
plot_uplift_curve(y_val, uplift_ct, trmnt_val, perfect=True);

Колоколообразная форма кривых показывает сильные положительные и отрицательные эффекты, присутствующие в наборе данных. Если бы эти эффекты отсутствовали, кривые были бы ближе к случайной линии.

Как выглядит кривая uplift без отрисовки идеальной кривой

Qini curve

Еще одной довольно распространенной кривой при оценке uplift моделей является Qini кривая, впервые введенная в статье [4] и определяющаяся следующим образом:

Формула qini curve

Qini curve, как и другие аплифт метрики, рассчитывается кумулятивно сразу для набора объектов. Кривую Qini для модели тоже сравнивают со случайной кривой (на графике черной линией) и с идеальным случаем (на графике красной линией). Аналогично с uplift кривой, чем выше кривая над случайной кривой, тем лучше. 

from sklift.viz import plot_qini_curve


# with ideal Qini curve (red line)
# perfect=True
plot_qini_curve(y_val, uplift_ct, trmnt_val, perfect=True);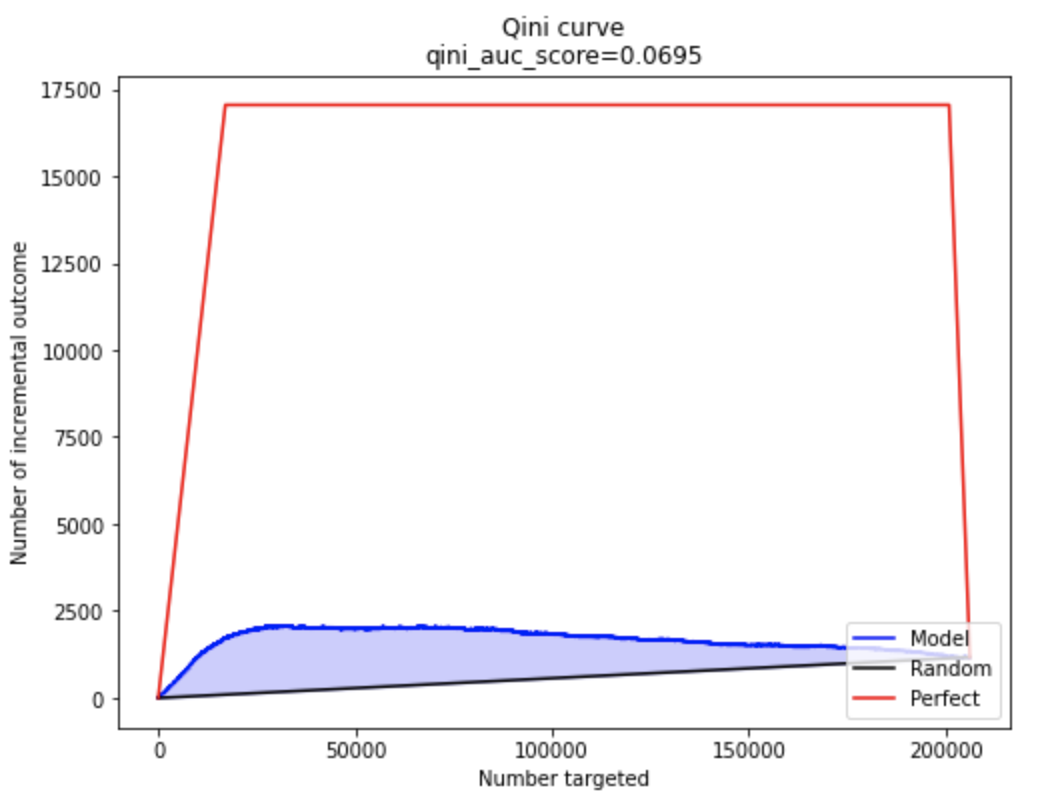

Физический смысл qini кривой в том, чтобы не давать модели поднимать наверх в ранжировании только целевую (treatment) группу, штрафуя ее за это множителем Nt/Nc, который уменьшает итоговое значение, если Nt сильно больше, чем Nc.

Можно провести очевидную параллель между uplift и qini кривыми: 

Например, когда контрольная и целевая группы сбалансированы, то qini кривая будет в два раза ниже, чем uplift.

Qini curve без идеальной кривой

От кривых к числам

Итак, теперь мы знаем, как строить qini и uplift кривые, с помощью которых можно оценить качество модели. При этом сравнивать модели хочется не "на глаз", а с помощью чисел. Как и во многих других метриках машинного обучения, основанных на кривых, предлагается рассчитывать площадь под модельными кривыми и нормировать ее на площадь под идеальной кривой [5]. При этом обычно из площадей под модельной и идеальной кривыми вычитают площадь под случайной кривой, которую называют baseline.

Qini coefficient или AUQC

В случае площади под qini кривой можно посчитать коэффициент qini, или area under qini curve (AUQC). Схематично его расчет можно нарисовать так:

from sklift.metrics import qini_auc_score


# AUQC = area under Qini curve = Qini coefficient
auqc = qini_auc_score(y_val, uplift_ct, trmnt_val) 
print(f"Qini coefficient on full data: {auqc:.4f}")

Qini coefficient on full data: 0.0695

Area under uplift curve, AUUQ

Для uplift кривой коэффициент называется AUUQ - area under uplift curve и считается аналогичным образом.

from sklift.metrics import uplift_auc_score


# AUUQ = area under uplift curve
auuc = uplift_auc_score(y_val, uplift_ct, trmnt_val) 
print(f"Uplift auc score on full data: {auuc:.4f}")

Uplift auc score on full data: 0.0422

Как вы могли заметить, коэффициенты AUQC и AUUC также отображаются на графиках кривых в названии графиков.

Заключение 

Целью наших статей (часть 1, часть 2, часть 3) был рассказ об основах uplift моделирования и кейсах его применения. Мы подробно разобрали не только основные методы и метрики, но и дизайн эксперимента для сбора обучающей выборки. Первые части были без кода, поэтому рекомендуем посмотреть практические туториалы здесь.

Мы надеемся, что они дадут базовые знания и возможность самостоятельно углубиться дальше в исследования. Например, на практике вы можете столкнуться с несколькими вариантами коммуникаций или предсказанием непрерывной целевой переменной. В этом вам помогут ссылки на источники. 

Статья написана в соавторстве с Максимом Шевченко @maks-sh

Источники

[1] Pierre Gutierrez, Jean-Yves Gerardy. Causal Inference and Uplift Modeling A review of the literature. JMLR: Workshop and Conference Proceedings 67:1–13, 2016

[2] Verbeke, Wouter & Baesens, Bart & Bravo, Cristian. Profit Driven Business Analytics: A Practitioner's Guide to Transforming Big Data into Added Value, 2018.

[3] Rene Michel, Igor Schnakenburg, Tobias von Martens. Targeting Uplift. An Introduction to Net Scores. Springer, 2019.

[4] Nicholas J. Radcliffe. Using control groups to target on predicted lift: Building and assessing uplift model. Direct Market J Direct Market Assoc Anal Council, 1:14–21, 2007.

[5] Floris Devriendt, Tias Guns, Wouter Verbeke. Learning to rank for uplift modeling. IEEE Transactions on Knowledge and Data Engineering, 2020