
В первой части мы познакомились с uplift моделированием и узнали, что метод позволяет выбирать оптимальную стратегию коммуникации с клиентом, а также разобрали особенности сбора данных для обучения модели и несколько базовых алгоритмов. Однако эти подходы не позволяли оптимизировать uplift напрямую. Поэтому в этой части разберем более сложные, но не менее интересные подходы.
Содержание статьи
Трансформация классов
Class Transformation approaсh, Class Variable Transformation approach, Revert Label approach
Достаточно интересный и математически подтвержденный подход к построению модели, представленный еще в 2012 году на ICML [1], который заключается в прогнозировании немного измененной целевой переменной.
где — новая целевая переменная -ого клиента
— целевая переменная -ого клиента
— бинарный флаг коммуникации: при — -й клиент попал в целевую (treatment) группу, где была коммуникация; при — -й клиент попал в контрольную (control) группу, где не было коммуникации.
Другими словами, новый класс равен 1, если мы знаем, что на конкретном наблюдении результат при взаимодействии был бы таким же хорошим, как и в контрольной группе, если бы мы могли знать результат в обеих группах:
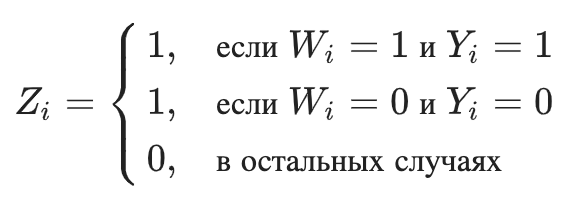

Распишем подробнее, чему равна вероятность новой целевой переменной:

В первой части статьи мы обсуждали, что обучающая выборка для моделирования uplift собирается на основе рандомизированного разбиения части клиентской базы на целевую и контрольную группы. Поэтому коммуникация не может зависеть от признаков клиента . Принимая это, мы имеем:
Получим:
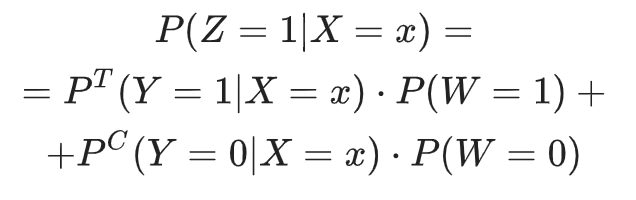
Также допустим, что , т.е. во время эксперимента контрольные и целевые группы были разделены в равных пропорциях. Тогда получим следующее:
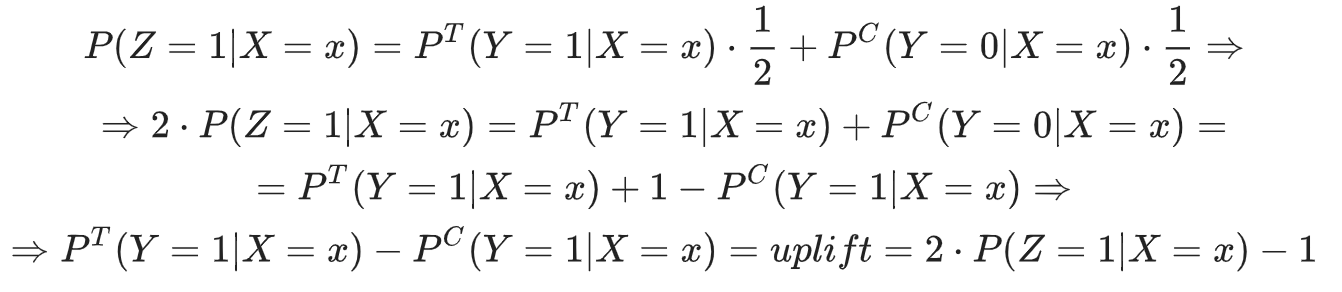
Таким образом, увеличив вдвое прогноз нового таргета и вычтя из него единицу, мы получим значение самого uplift, т.е.
Исходя из допущения, описанного выше: , данный подход следует использовать только в случаях, когда количество клиентов, с которыми мы прокоммуницировали, равно количеству клиентов, с которыми коммуникации не было.
Трансформация классов (регрессия)
Transformed outcome
На предыдущий тип трансформации классов накладываются серьезные ограничения: целевая переменная может быть только бинарной, а контрольная и целевая группы должны быть распределены в равных пропорциях. Давайте рассмотрим более общий подход из [2], не имеющий таких ограничений.
Трансформируем исходную целевую переменную по следующей формуле:
Где — новая целевая переменная для -ого клиента
— флаг коммуникации для -ого клиента
— propensity score или вероятность отнесения к целевой группе:
Здесь важно отметить, что можно оценить как долю объектов с в выборке. Или воспользоваться способом из [3], в котором предлагается оценить как функцию от , обучив классификатор на имеющихся данных , а в качестве целевой переменной взяв вектор флага коммуникации .
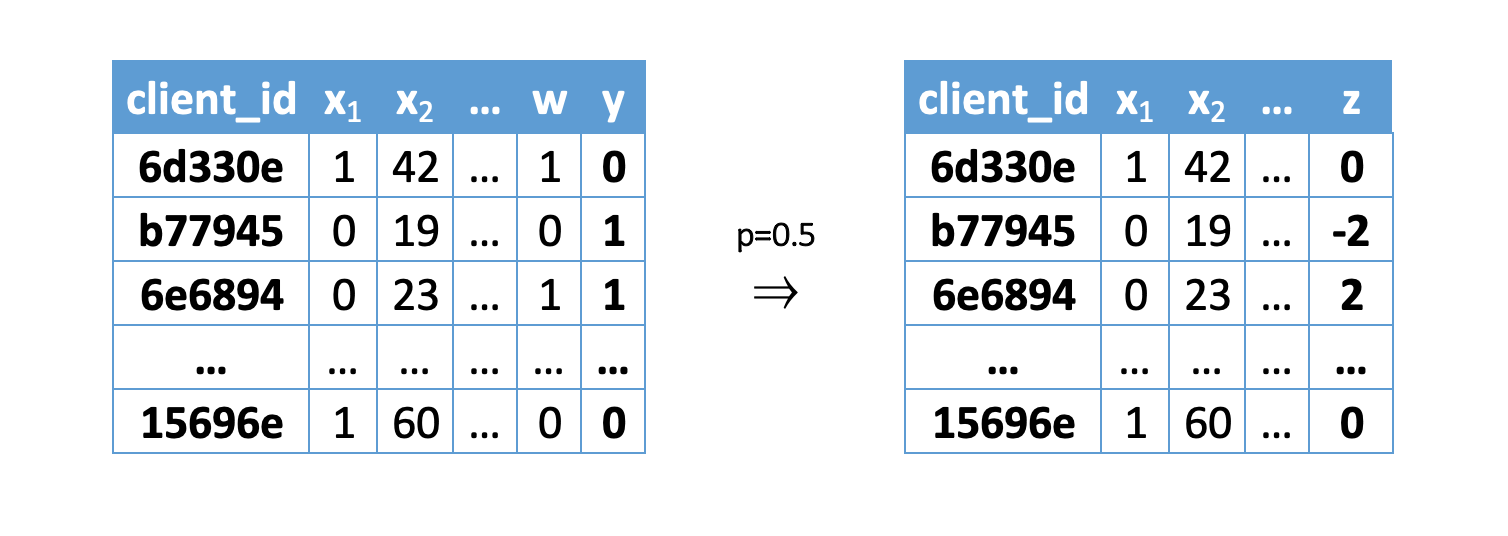
После применении формулы получаем новую целевую переменную и можем обучить модель регрессии с функционалом ошибки . Так как именно при применении MSE предсказания модели являются условным математическим ожиданием целевой переменной.
Покажем, что условное матожидание трансформированного таргета и есть желаемый causal effect из первой части статьи:
Напомним также, что наблюдаемую целевую переменную можно представить в виде:
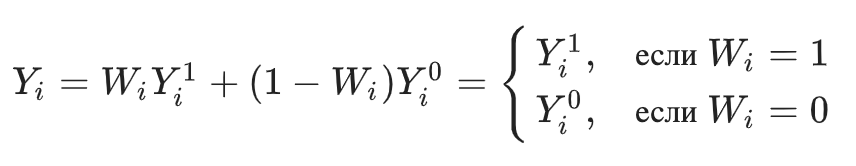
Где — потенциальные реакции для каждого -го объекта в зависимости от значения , которые мы хотели бы (но не можем) наблюдать одновременно.
Перепишем формулу трансформации с учетом этого:
Тогда:
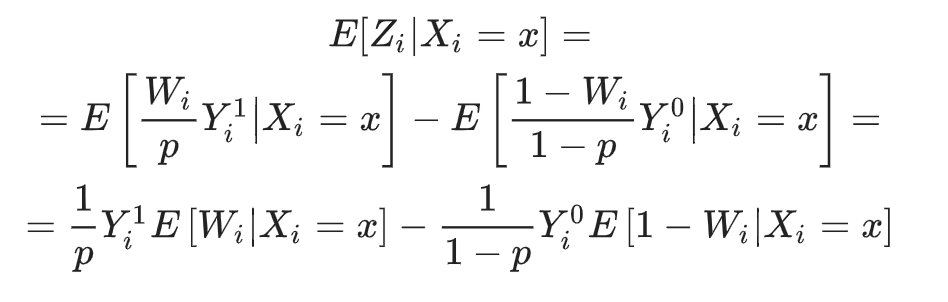
Так как при случайном разбиении на целевую и контрольную группы не должно зависить от , то:
Получим, что преобразованная целевая переменная позволяет оценивать uplift:

Многоклассовая модель
Generalized Lai Method
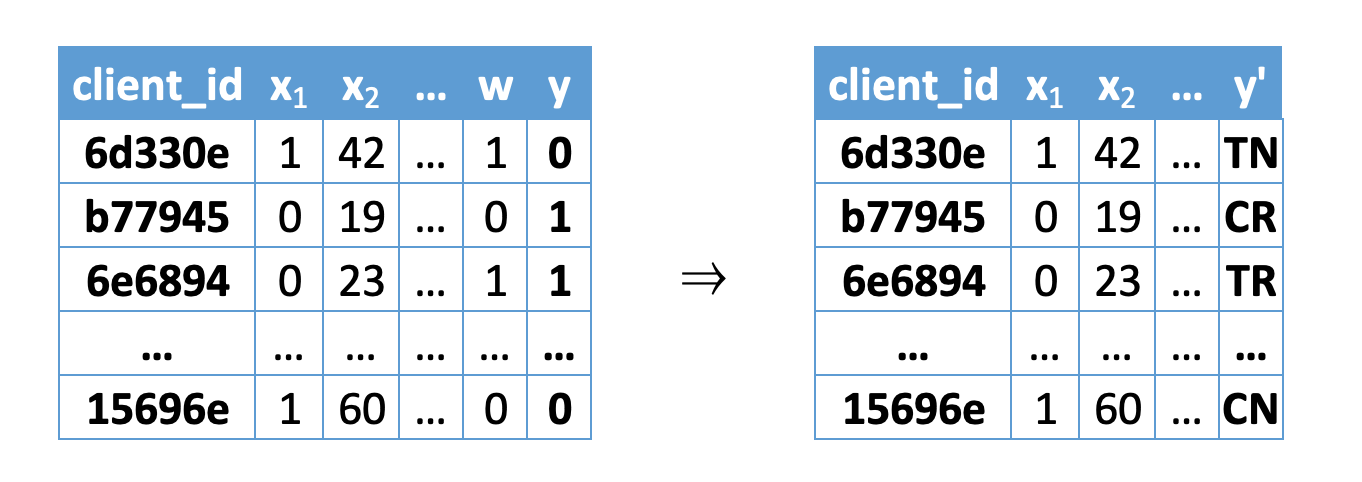
Так как мы можем взаимодействовать с клиентами и наблюдать их реакцию , то разделим их на 4 непересекающихся класса:
- Клиент выполнил целевое действие и мы с ним не коммуницировали (Control Responder — CR):
- Клиент не выполнил целевое действие и мы с ним не коммуницировали (Control Non-Responder — CN):
- Клиент выполнил целевое действие и мы с ним коммуницировали (Treated Responder — TR):
- Клиент не выполнил целевое действие и мы с ним коммуницировали (Treated Non-Responder — TN):

Картинка взята и адаптирована из [4]
Попробуем разобраться, как соотносятся между собой обозначенные выше 4 класса и типы клиентов из первой части, которых мы хотим найти (не беспокоить, потерянный, лояльный, убеждаемый). Их главное различие в том, что классы CR, CN, TR, TN мы можем наблюдать непосредственно по их реакции на коммуникацию, в то время как типы клиентов мы наблюдать не можем. При этом они связаны между собой: каждый из четырех классов может содержат по 2 типа клиента одновременно.
- Так как мы не знаем, выполнил бы CR клиент целевое действие при нашем воздействии, то он относится либо к не беспокоить , либо к лояльным клиентам. Проводя аналогичные рассуждения, рассмотрим остальные классы:
- среди CN клиентов могут быть как потерянные, так и убеждаемые типы клиентов
- Среди TR клиентов могут быть как убеждаемые, так и лояльные типы клиентов
- Среди ТN клиентов могут быть как не беспокоить, так и потерянные типы клиентов
В этом подходе [4] предлагается прогнозировать вероятности отнесения клиента к каждому из этих 4 классов и обучить модель многоклассовой классификации:
Тогда uplift можно будет рассчитать следующим образом:
Мы суммируем вероятности принадлежности к классам и , так как они содержат тип убеждаемый, который мы хотим найти, и вычитаем вероятности принадлежности к классам и , так как они содержат тип не беспокоить, которого наоборот хотелось бы избежать.
Когда выборки по своему объему сильно не сбалансированы, предлагается рассчитывать uplift так:
Где — доля клиентов в тестовой группе, — доля клиентов в контрольной группе, .
Нормировка необходима тогда, когда целевая группа мала по сравнению с контрольной группой, так как в этом случае доля TR и TN клиентов также будет небольшой.
Методы, основанные на деревьях
Decision trees for uplift modeling, Causal trees
Стоит отметить, что предыдущие методы имеют следующие недостатки:
- В методах с двумя моделями при расчете финального предсказания учитываются результаты двух моделей, а значит их ошибки суммируются;
- Если для обучения будут использоваться принципиально разные модели или природа данных целевой и контрольной групп будут сильно отличаться, то может потребоваться калибровка предсказаний моделей;
- Так как во многих методах uplift прогнозируется косвенно, модели могут пропускать слабые различия между целевой и контрольной группах.
Хочется взять хорошо зарекомендовавший себя метод и изменить его так, чтобы непосредственно оптимизировать аплифт. Например, авторы статьи [5] предлагают использовать деревья решений с другим критерием разбиения. Дерево строится так, чтобы максимизировать расстояние (дивергенцию) между распределениями целевой переменной у контрольной и целевой групп. Формально для каждого разбиения это можно записать так:
Где — распределения целевой переменной в контрольной и целевой группах
— дивергенция (расхождение) между двумя распределениями
Есть несколько видов дивергенции D, которые используют для решения этой задачи:
- Дивергенция Кульбака—Лейблера (Kullback–Leibler divergence):
- Евклидово расстояние (Euclidean distance):
- Дивергенция хи-квадрат (Сhi-squared divergence):
Где распределения представлены как
Если получается так, что в вершине при разбиении остаются объекты одной группы (контрольной или целевой), то дивергенция сводится к стандартному для деревьев критерию (KL-дивергенция — к энтропийному критерию, Евклидово расстояние и хи-квадрат — к критерию Джини).
Также важное условие разбиения — это сведение к минимуму разницы между количеством объектов, попавших в левую и правую дочернюю вершину. Слева на картинке изображен пример плохого разбиения, когда высокое значение величины uplift в левой дочерней вершине достигается за счет того, что в него попало всего 30 объектов из 1000.

Картинка взята и адаптирована из [7]
Чтобы контролировать количество объектов в разбиении, можно воспользоваться формулой взвешенной дивергенции (после разбиения):
Где и — количество объектов, попавших в левую и правую дочернюю вершину соответственно
— распределения целевой переменной в целевой и контрольной группе для левой и правой дочерних вершин
После реализации дерева с новым критерием разбиения можно использовать этот алгоритм в качестве базового алгоритма в ансамблях, например, в случайном лесе или градиентном бустинге, а также применять стандартные для деревьев методы борьбы с переобучением, такие как стрижка (pruning) или ранняя остановка (early stopping).
Заключение
Цикл обзорных статей не раскрывает всех подходов к прогнозированию uplift, однако охватывает наиболее популярные и интересные для нас. На сегодняшний день не существует идеального метода, который на разных данных и на протяжении долгого времени выигрывал бы по качеству у других. Этот факт мотивирует исследователей разрабатывать новые подходы (например, любопытная статья 2019 года о применении бандитов к решению данной задачи [8]). В дальнейшем мы планируем рассмотреть метрики качества для оценки прогнозируемого uplift.
Uplift моделирование используется не только для задач маркетинга, но и в медицине, политике, экономике и в других сферах. То есть, когда поведение объектов может изменяться под некоторым контролируемым воздействием, такой подход может быть более предпочтительным, чем другие.
Статья написана в соавторстве с Максимом Шевченко (maks-sh)
Источники
- [1] Maciej Jaskowski and Szymon Jaroszewicz. Uplift modeling for clinical trial data. ICML Workshop on Clinical Data Analysis, 2012.
- [2] Susan Athey and Guido W Imbens. Machine learning methods for estimating heterogeneouscausal effects. stat, 1050:5, 2015.
- [3] P. Richard Hahn, Jared S. Murray, and Carlos Carvalho. Bayesian regression tree models for causal inference: regularization, confounding, and heterogeneous effects. 2019.
- [4] Kane, K., V. S. Y. Lo, and J. Zheng. Mining for the Truly Responsive Customers and Prospects Using True-Lift Modeling: Comparison of New and Existing Methods. Journal of Marketing Analytics 2 (4): 218–238. 2014.
- [5] Piotr Rzepakowski and Szymon Jaroszewicz. Decision trees for uplift modeling with single
and multiple treatments. Knowledge and Information Systems, 32(2):303–327, 2012. - [6] Yan Zhao, Xiao Fang, and David Simchi-Levi. Uplift modeling with multiple treatments and general response types. In Proceedings of the 2017 SIAM International Conference on Data Mining, 588–596. SIAM, 2017.
- [7] Wouter Verbeke, Bart Baesens, Cristian Bravo. Profit Driven Business Analytics: A Practitioner's Guide to Transforming Big Data into Added Value.
- [8] Jeroen Berrevoets, Sam Verboven, Wouter Verbeke. Optimising Individual-Treatment-Effect Using Bandits, 2019.

