14.04.2021 07:23
vagonoff 0 975 Источник
image
Привет, Хабр.

Маркетинговая оптимизация, установка лимитов по портфелю кредитных продуктов, логистика и товарная аналитика, оптимизация производственных процессов, … — список применения методов математической оптимизации далеко не ограничивается перечисленными задачами, а методы оптимизации начали решать задачи бизнеса задолго до того, как науки о данных стали называться науками о данных.

С развитием адаптации технологий ML/DS можно ожидать рост популярности оптимизационных методов прежде всего за счет того, что решения бизнес задач становятся более комплексными. То есть, вместо того, чтобы сделать одну-две модели, которые выдают почти финальные решения, процесс принятия решения декомпозируется на отдельные составляющие компоненты, в которых есть место прогнозным моделям, а для самого принятия решения с учетом всех этих компонент и ограничений работает уже оптимизационная модель.

В статье поговорим о возможной постановке задачи оптимизации в банковской сфере и методах ее решения.

В команде GlowByte Advanced Analytics мы активно продвигаем подход, согласно которому проекты по ML лучше изначально формулировать как задачи оптимизации, то есть как систему поддержки принятия решений с измеримыми бизнес-показателями.

Существует много открытых фреймворков для решения оптимизационных задач таких как Gekko, Pyomo, Python-mip, а так же различное проприетарное ПО типа IBM ILOG CPLEX Optimization Studio.

План статьи




Задача оптимизации


Задача оптимизации заключается в нахождении экстремума целевой функции в области пространства, ограниченной некоторым набором условий (равенств и/или неравенств). В зависимости от типа целевой функции и типа ограничений задачи оптимизации делятся на задачи линейного и нелинейного программирования.
В общем виде математическая постановка задачи может выглядеть следующим образом

image

Т.е. среди всех векторов множества $X$, которое ограничено условиями $g_{i}(\vec{x}) \leq 0$ и $h_{k}(\vec{x}) = 0,$ необходимо найти такой вектор $\vec x^* $, при котором значение $f(\vec{x}^*)$ будет минимальным на всем множестве $X$.
При линейных ограничениях и линейной целевой функции задача (1) относится к классу задач линейного программирования и может быть решена симплекс-методом.

Маркетинговая оптимизация в банке


Представим себе современный банк, работающий с физическими лицами и продающий им свои основные продукты: кредитные карты, кредиты наличными и т.д. Каждому клиенту банк может предложить один из продуктов $P_i, \; i = 1, \ldots, n$ в одном из доступных для коммуникации каналов $C_{k}, \; k = 1, \ldots, m$ (звонок, смс и т.д.). При этом количество доступных для отправки в неделю/месяц коммуникаций в каждом канале (объем канала) ограничено

$\begin{aligned} &\sum Calls \leq N_1 \\ &\sum Sms \leq N_2 \\ &\sum Email \leq N_3 \\ &\sum Push \leq N_4 \\ \end{aligned} \;\;\;(2)$


Предположим, что в банке имеется модель (или несколько моделей), которая с хорошей точностью предсказывает вероятность отклика клиента на определенный банковский продукт в определенном канале. Оценить качество такой модели с точки зрения того, как ее оценки соотносятся с реальными вероятностями, можно, построив на отложенной выборке распределение прогнозной вероятности и реального отлика по бакетам скора модели.

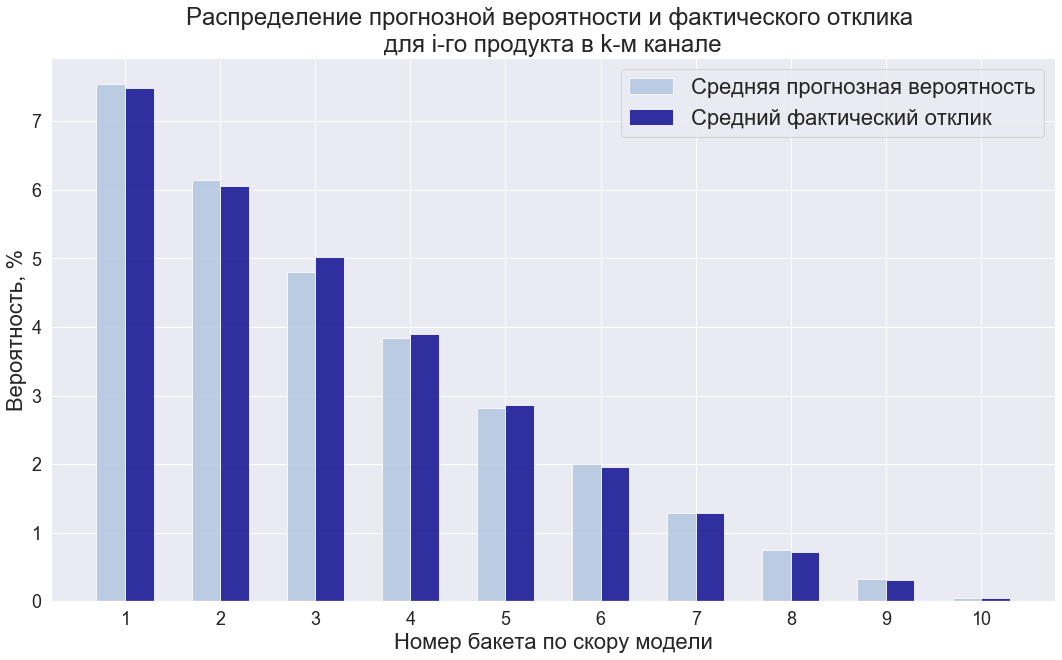
image

Рис. 1

Теперь, имея на руках в таблице в базе данных для каждого клиента вероятности отклика на отдельные продукты в определенном канале, ограничения на объем коммуникаций (2) и тот факт, что за одну коммуникацию можно предложить клиенту только один продукт, зададимся вопросом, а какой именно продукт и в каком канале лучше всего предложить каждому из доступных для коммуникации клиентов?

image


При постановке задачи важно понимать, какую именно метрику мы хотим максимизировать на выходе. Например, если в результате коммуникаций мы хотим получить максимальный отклик, то соответствующая задача оптимизации может быть поставлена следующим образом

$\begin{cases} p_{11}x_{11} + p_{12}x_{12} + p_{13}x_{13} + p_{21}x_{21} + p_{22}x_{22} + p_{31}x_{31} + p_{32}x_{32} + p_{33}x_{33} \rightarrow \max \\\\ Одному \;клиенту\; не\; более \; одного\; продукта \\ x_{11} + x_{12} + x_{13} \leq 1 \\ x_{21} + x_{22} \leq 1 \\ x_{31} + x_{32} + x_{33} \leq 1 \\ \\ Ограничение \; количества \; звонков \\ x_{12} + x_{21} + x_{31} \leq N_1 \\ \\ Ограничение \; количества \; смс \\ x_{13} + x_{22} + x_{33} \leq N_2 \\\\ Ограничение \; количества \; имейлов\\ x_{11} + x_{32} \leq N_3 \\ \\ x_{ik} \in \left\{0, 1 \right\} \end{cases} \;\;\; (3)$


Это классическая задача линейного программирования, которая легко решается с помощью открытых фреймворков, упомянутых выше.

В случае, если целью коммуникаций будет максимизация будущей доходности, то целевую функцию в задаче (3) можно записать в виде

$\begin{aligned}D_{11}p_{11}x_{11} + D_{12}p_{12}x_{12} + D_{13}p_{13}x_{13} &+D_{23}p_{21}x_{21} + D_{22}p_{22}x_{22} +\\+ D_{34}p_{31}x_{31} + D_{32}p_{32}x_{32} + &D_{32}p_{33}x_{33} \rightarrow \max,\end{aligned}\;\;\; (4)$


где $D_{ik}$ — доходность от k-го продукта на i-м клиенте. Значения $D_{ik}$ могут быть получены с помощью прогнозных моделей или оценены каким-то другим способом.

Замечания
  1. Описанные выше подходы предполагают, что мы имеем достаточно хорошие прогнозы/оценки для $p_{ik}$ и $D_{ik}.$
  2. Если скоры $p_{ik}$ для различных продуктов получены от разных моделей и при этом они (скоры) плохо согласуются с реальной вероятностью отклика (это можно увидеть, например, по графику как на Рис. 1), то перед оптимизацией их необходимо откалибровать. Про различные способы калибровки можно почитать по ссылке.
  3. Предполагается также, что количество коммуникаций, на которые банк готов потратить средства, меньше, чем количество клиентов, которым банк готов предложить свои продукты. В противном случае оптимизировать будет нечего.


Немного кода


Попробуем решить задачу маркетинговой оптимизации, поставленную в виде (3), с помощью библиотеки MIP, упомянутой выше. Возьмем случайным образом сгенерированный датасет объемом в 6000 строк, в котором содержится 1000 клиентов, каждому из которых можно предложить один из 3-х продуктов в двух каналах — SMS и звонок.

Код 
import pandas as pd
from mip import Model, MAXIMIZE, CBC, BINARY, OptimizationStatus, xsum

frame = pd.read_csv('table_for_optimization.csv')
frame.head()


image

Предположим, что у нас есть ограничение на объем коммуникаций: 500 SMS и 200 звонков. Напишем функцию для решения задачи оптимизации.

Код 

def optimize(frame: pd.DataFrame, channel_limits: dict) -> list:
    """
    Возвращает массив оптимальных предложений
    """
    
    df = frame.copy()
    
    #создание модели
    model = Model(sense=MAXIMIZE, solver_name=CBC)

    #вектор бинарных переменных задачи
    x = [model.add_var(var_type=BINARY) for i in range(df.shape[0])]
    df['x'] = x

    #целевая функция
    #функция xsum значительно ускоряет суммирование https://docs.python-mip.com/en/latest/classes.html#mip.xsum    
    model.objective = xsum(df['score'] * df['x'])

    #ограничения на количество коммуникаций в каждом канале
    for channel in df.channel.unique():
        model += (xsum(df[df.channel==channel]['x']) <= channel_limits[channel])

    #ограничения на количество продуктов для каждого клиента (не более одного продукта на клиента)
    for product_cnt in df.groupby(['client_id'])['x'].apply(xsum):
        model += (product_cnt <= 1)
        
    status = model.optimize(max_seconds=300)
    
    del df
    
    if status == OptimizationStatus.OPTIMAL or status == OptimizationStatus.FEASIBLE:
        return [var.x for var in model.vars]
    elif status == OptimizationStatus.NO_SOLUTION_FOUND:
        print('No feasible solution found')


Зададим ограничения на объем коммуникаций в каналах, запустим решение задачи оптимизации и посмотрим как в итоге распределятся оптимальные предложения по каналам и продуктам.

Код 

#объем доступных коммуникаций в каналах
CHANNELS_LIMITS = {
    'call': 200,
    'sms': 500
}

optimal_decisions = optimize(frame=frame, channel_limits=CHANNELS_LIMITS)
frame['optimal_decision'] = optimal_decisions

#распределение продуктов в каналах
frame[frame['optimal_decision']==1].groupby(['channel', 'product']).                                    agg({'client_id': 'count'}).                                    rename(columns={'client_id': 'client_cnt'})


image

Весь код и данные доступны по ссылке.

P.S.


В зависимости от типа прогнозных моделей мы можем располагать не просто средней оценкой вероятности отклика $p_{ik},$ а также иметь распределение этого значения для каждого клиента и продукта. В таком случае задача оптимизации (3) может быть дополнена условием

$\sum (отклик \;с \;вероятностью \geq K ) \geq N. \;\;\; (5)$


Более того, если в нашем распоряжении есть распределение для каждой вероятности $p_{ik}$, то мы можем также решать и обратную задачу: минимизировать количество коммуникаций при условях типа (5) с учетом определенных ограничений, задаваемых бизнесом.

Благодарю коллег из команды GlowByte Advanced Analytics за помощь и консультации при подготовке этой статьи.