Представьте, что у вас нет под рукой калькулятора (но есть циркуль и линейка или угольник) и вам нужно посчитать результат в виде отрезка. Задача решается за менее чем 5 простых шагов.

Базовая формула вычисления

Для начала докажем одну формулу, которая нам будет помогать с дальнейшим решением.

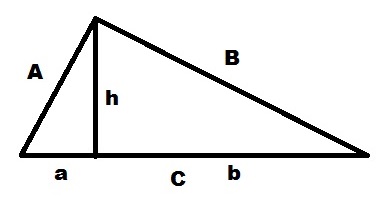
В прямоугольном треугольнике ABC проведем высоту h на сторону C. По теореме Пифагора выводим:

Подставляем всё в первую формулу:

И если раскрыть скобки:

После сокращения получаем:

Вот с помощью этой формулы и будем выводить наши решения.

Единичная мера длины

Так как мы вычисления проводим на плоскости с отрезками, нам необходимо определиться с мерой единичной длины равной 1. Если мы отложим отрезок 1 дециметр, то он так же будет равен 10 сантиметрам, 100 миллиметрам или 4 дюймам. Один отрезок и 4 разных чисел разной меры длины его определяют. Что бы выбрать одну систему счисления длин отрезков, примем за единицу длины какой-то отрезок. Какой - определим по ходу расчетов, и он зафиксирует нужную меру длины.

Циркуль как универсальный инструмент

Циркуль удобно использовать как средство:

• отмерить отрезок определенной длины, при этом знать величину этой длины совершенно нет надобности.

• прочертить дугу на одинаковом расстоянии от определённой точки.

• отложить перпендикуляр к линии через определённую точку. Для этой цели удобнее использовать угольник с прямым углом, чем циркулем чертить 4 дуги.

Вычисление квадрата длины

Для вычисления квадрата величины X используем нашу формулу в виде:

Чертим прямую линию достаточной длины.

Откладываем на ней отрезок единичной длины.

От правого конца единичного отрезка 1 откладываем вверх перпендикуляр длиной X.

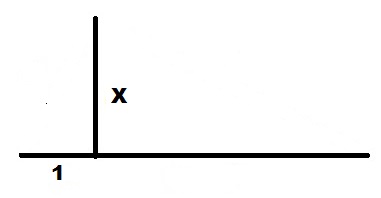
Проводим линию от левого конца единичного отрезка 1 до верхнего конца отрезка X.

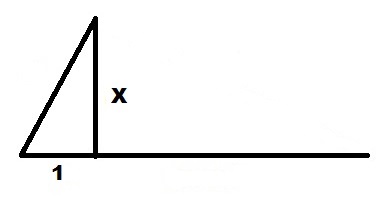
От этого отрезка откладываем перпендикуляр на линию продолжения единичного отрезка 1. Их пересечение и есть правый край квадрата длины. Левый край начинается от точки, где отложена высота.

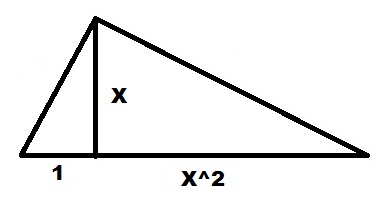
Пример. У вас есть какой-то квадрат, со стороной X, начерченный на плоскости или на земле. Нужно узнать его площадь в попугаях. Одна сторона квадрата длиной X у нас уже есть. На соседней стороне откладываем длину одного попугая (там где 1 находится). Соединяем концы линией, откладываем перпендикуляр, продлеваем отрезок с попугаями до перпендикуляра и получаем решение в квадратных попугаях.

Вычисление квадратного корня длины

Для вычисления квадратного корня величины используем нашу формулу в виде:

Чертим прямую линию достаточной длины.

Откладываем на ней единичный отрезок длины 1.

На продолжении единичного отрезка откладываем отрезок длины X.

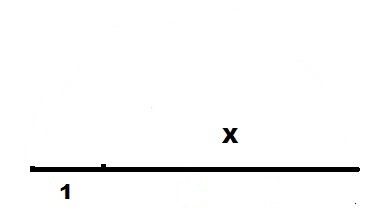
Полученный отрезок 1+X делим пополам с помощью циркуля и получаем точку O. Как это сделать, приводить здесь не буду, это задачка из школьного курса. Обозначим длину найденной половины как R.

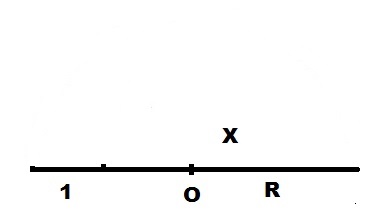
Вокруг центра O, циркулем нарисуем дугу радиусом R.

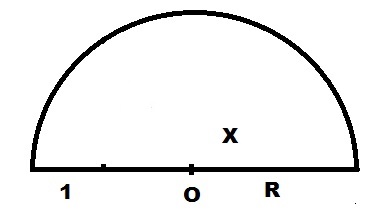
От правого конца отрезка 1 отложим вверх перпендикуляр до пересечения с дугой окружности. Длина этого перпендикуляра и будет равна корню квадратному из длины X.

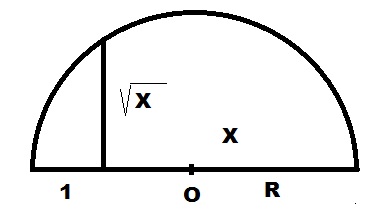
Вычисление обратной величины длины

Для вычисления обратной величины длины используем нашу формулу в виде:

Решение очень похоже на нахождение квадрата величины, только a и h меняются местами.

Чертим прямую линию достаточной длины.

Откладываем на ней отрезок длины X.

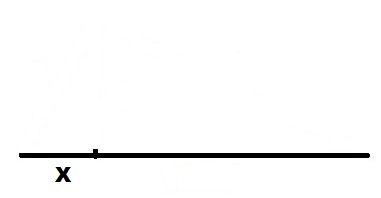
От правого края отрезка X откладываем вверх перпендикуляр единичной длины 1.

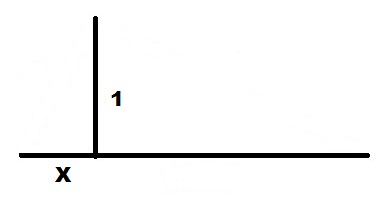
Соединяем концы отрезков линией.

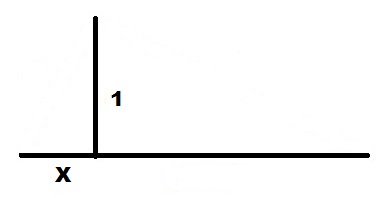
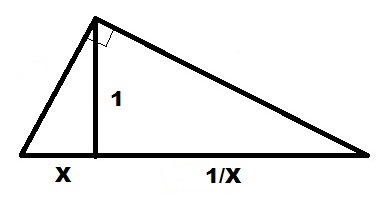
От верхнего конца отрезка X откладываем перпендикуляр к линии продолжения отрезка 1. Полученный отрезок и есть решение.

Выводы

Приведенные выкладки удобны, когда не хочется возиться с цифрами и их арифметическими вычислениями, которые всё равно будут обратно приложены к длинам отрезков.

Если величина X сильно отличается от единичного отрезка 1, ошибка вычисления может быть значительной. Но если применить масштабирование, то ошибку можно значительно уменьшить. Например, при захождении корня длины 20, его можно поделить на 16 (4 раза поделить пополам), а потом ответ умножить на 4 (4 раза отложить полученный отрезок).