В этой заметке я хочу описать два типа графиков для одномерных данных, а именно

• гистограмма
• ящик с усами

Рассмотрим произвольную выборку вещественных чисел , будем обозначать порядковую статистику , такую что .

Гистограмма

Скорее всего все поменять этот тип графика из школьной или университетской программы, который выглядит приблизительно так как на картинке.



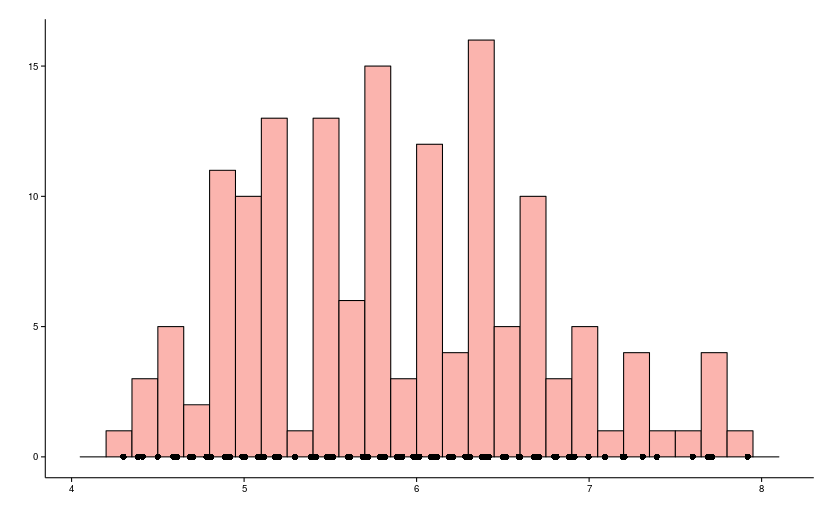
Прежде всего необходимо помнить, что значения входной выборки располагаются по оси x, а по оси y располагается число раз, которое данное значение встретилось (назовем их отсчеты). Гистограмма позволяет огрубить и сделать набор данных более компактным, при этом не умаляя его специфичность.
Важными характеристиками гистограммы являются следующие:

• число столбцов (которые называются bins или bars)
• абсолютные или плотностные отсчеты по оси y
• как сгруппированы данные

Столбцы

В подавляющем большинстве случаев гистограмма определена на отрезке , где — исходная выборка, вспомогательные константы, округляющие до ближайших “читаемых” чисел, которые в каждом случае зависят от масштаба и, обычно, это делители десятки в масштабе исходных данных. Если вдруг стало интересно, как ставить отсечки в данных, то можно посмотреть ссылку: R (pretty).

Так же обычно гистограммы делят отрезок I на подотрезки равной длины и, вот, выбор числа отрезков является искусством, хотя можно привести несколько формул:

• Правило Стёрджеса (Не фотограф).
• Правило Скотта.
• Правило Фридмана-Дьякониса.

где — число столбцов, — размер исходной выборки, — оценка стандартного отклонения, — интерквартильное расстояние, которое еще встретится ниже.

Так же можно отметить несколько правил здравого смысла:

• хорошо чтобы в большинстве столбцов было больше одного исходного значения
• каждый столбец гистограммы требует хотя бы одного пикселя по ширине, и в целом ограничение “не более 200” столбцов достаточно распространено

В противном случае, если число столбцов избыточно, а исходных данных мало, гистограмма будет напоминать штрих-код, как например на рисунке ниже.

Ось Y

Гистограммы бывают в абсолютных значениях, когда по оси y откладывается количество элементов исходной выборки попавших в каждый из интервалов, и в относительных, когда сумма столбцов нормируются на единицу, в этом случае гистограмма является оценкой плотности распределения и с точки зрения графика меняется лишь масштаб.

Так как обычная гистограмма является оценкой плотности, то мы можем суммировать столбцы и получить оценку функции вероятности следующим образом: . Два следующих графика построены по одним и тем же данным, слева не нормализованная гистограмма, справа аккумулированные значения нормализованной гистограммы.

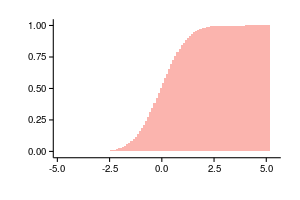
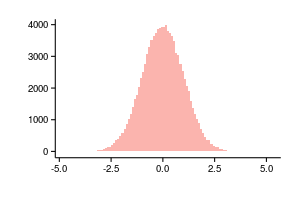
Группировка данных

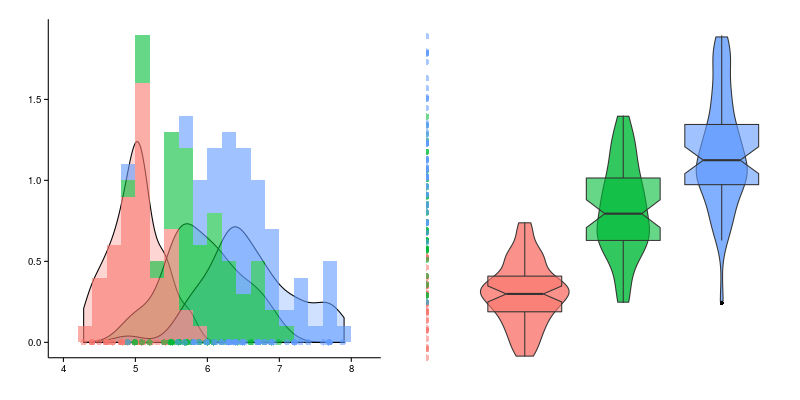
До сих пор был рассмотрен случай, когда у нас есть характеристика, на которую мы просто хотим взглянуть, обычно намного более интересно сравнивать поведение одной и той же характеристики для различных подгрупп. В таком случае гистограмма будет иметь следующий вид.



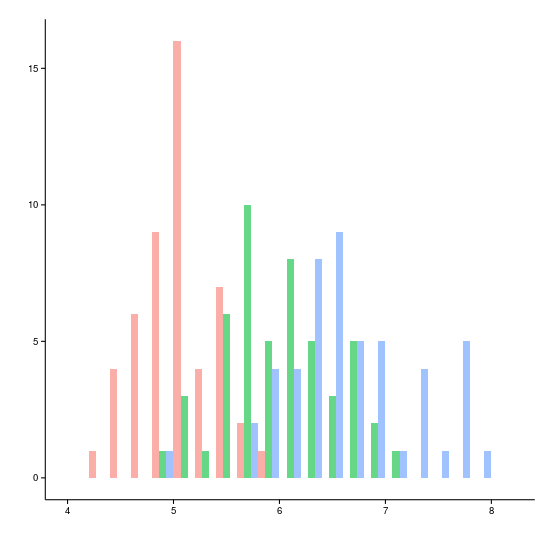
В данном случае, ширина каждого столбца для каждой группы уменьшается пропорционально числу групп и слегка сдвигаются друг относительно друга, в качестве альтернативы можно рассмотреть полупрозрачное перекрытие, которое будет выглядеть следующим образом для тех же данных.

В сухом остатке

Для отрисовки гистограммы необходимо определить

• Число столбцов
• Нужна ли нормализация и аккумулирование данных
• Способ отображения различных групп

Для отрисовки гистограммы для каждой группы требуется хранить следующие значения:

• значение границ столбцов, где самое первое значение -координата левой границы самого левого столбца, а последнее — -координата правой границы самого правого столбца
• значений — количество элементов попавших в каждый из столбцов.

Диаграмма размаха

“Ящик с усами” не имеет официально устоявшегося названия, а называть его “ящиком с усами“ у меня язык не поворачивается, тем более когда ящиков несколько, а диаграмма размаха хоть и не очень частотное, но более благозвучное название. Приведем пример трех ящиков слева отображены соответствующие значения исходных данных (не являются частью диаграммы размаха). Прежде всего необходимо отметить, что в случае диаграмм размаха, исходная характеристика откладывается по оси Y, а ось X условна и представляет собой группирующую переменную.



Чтобы нарисовать ящик для одной группы про исходные данные необходимо знать всего три характеристики:

• Первый квартиль
• Медиану
• Третий квартиль

Иногда к “обязательному” набору добавляют следующие дополнительные:

• Минимум
• Максимум
• Пятипроцентный персентиль
• Девяностопятипроцентный персентиль
• Множество экстремальных значений ,

Таким образом, ящик с усами в разрезе будет выглядеть следующим образом.



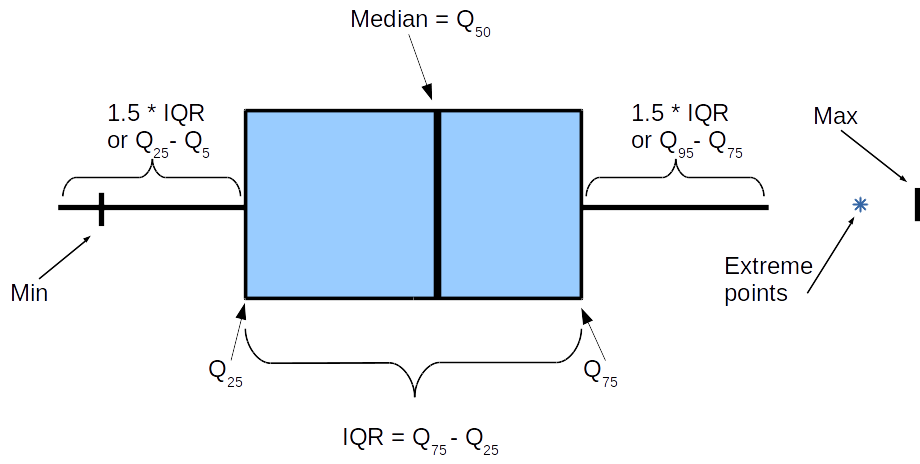
Некоторые моменты требуют пояснения. Ящик, то есть объект между и , практически везде ограничен этими значениями, а вот “усы” могут различаться и если вас действительно интересуют числа, необходимо уточнять, что имеется в виду в каждом отдельном случае. Самое важное это длина усов: исходим из того, что она .

Отметки минимума и максимума часто опускаются, экстремальные точки, то есть выходящие за пределы усов тоже опускаются либо рисуются точками или звездочками. В зависимости от структуры данных желание отрисовывать экстремальные значения может значительно увеличить объем данных для отрисовки диаграммы размаха.

Магическое число появилось в работе Тьюки Exploratory Data Analysis (1977) и причина его появления не очень ясна, но с тех времен ничего не менялось, многие инструменты предлагают его в качестве значения по умолчанию, но позволяют выставлять произвольное, вплоть до нуля, в этом случае, “усы” будут покрывать весь отрезок от минимального до максимального значений исходных данных.

Есть предположение, что возникло следующим образом. Ширина усов составляет , известно, что для симметричных распределений совпадает с абсолютным отклонением от медианы (MAD), которая в свою очередь, является оценкой дисперсии с коэффициентом . А значит, , мы получаем не безызвестные 3 сигмы влево, 3 сигмы вправо.
Иногда в качестве концов усов предлагается интервал , в таком случае очевидно, что всегда (если исходных данных больше 20) должны получаться точки, не попадающие внутрь интервала и поэтому их обычно игнорируют при таком подходе.

В сухом остатке

Для отрисовки “диаграммы размаха” необходимо определить:

• способ группировки данных
• длину усов
• нужно ли отмечать экстремальные значения

Для отрисовки “ящика с усами” для одной группы требуется всего 3 числа.