25.05.2021 02:40
uchitel 2 2900 Источник

Доброго времени суток, хабраледи и хабраджентельмены! В этой статье мы продолжим погружение в статистику вместе с Python. Если кто пропустил начало погружения, то вот ссылка на первую часть. Ну, а если нет, то я по-прежнему рекомендую держать под рукой открытую книгу Сары Бослаф "Статистика для всех". Так же рекомендую запустить блокнот, чтобы поэкспериментировать с кодом и графиками.

Как сказал Эндрю Ланг: "Статистика для политика – все равно что уличный фонарь для пьяного забулдыги: скорее опора, чем освещение." Тоже самое можно сказать и про эту статью для новичков. Вряд ли вы почерпнете здесь много новых знаний, но надеюсь, эта статья поможет вам разобраться с тем, как использовать Python для облегчения самостоятельного изучения статистики.

Зачем выдумывать новые распределения?

Представим... так, прежде чем нам что-то представлять, давайте снова сделаем все необходимые импорты:

import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
import seaborn as sns
from pylab import rcParams
sns.set()
rcParams['figure.figsize'] = 10, 6
%config InlineBackend.figure_format = 'svg'
np.random.seed(42)

А вот теперь давайте представим, что мы пивовары, придумавшие рецепт и технологию варки классного пива. Продажи идут хорошо, да и в целом все неплохо, но все-таки очень интересно, как потребители оценивают качество нашего пива. Мы решили опросить 1000 человек и оценить качество напитка по 100-бальной шкале в сравнении с другими сортами пива, которые им доводилось пробовать ранее. Данные опроса могли бы выглядеть так: 

gen_pop = np.trunc(stats.norm.rvs(loc=80, scale=5, size=1000))
gen_pop[gen_pop>100]=100
print(f'mean = {gen_pop.mean():.3}')
print(f'std = {gen_pop.std():.3}')
mean = 79.5
std = 4.95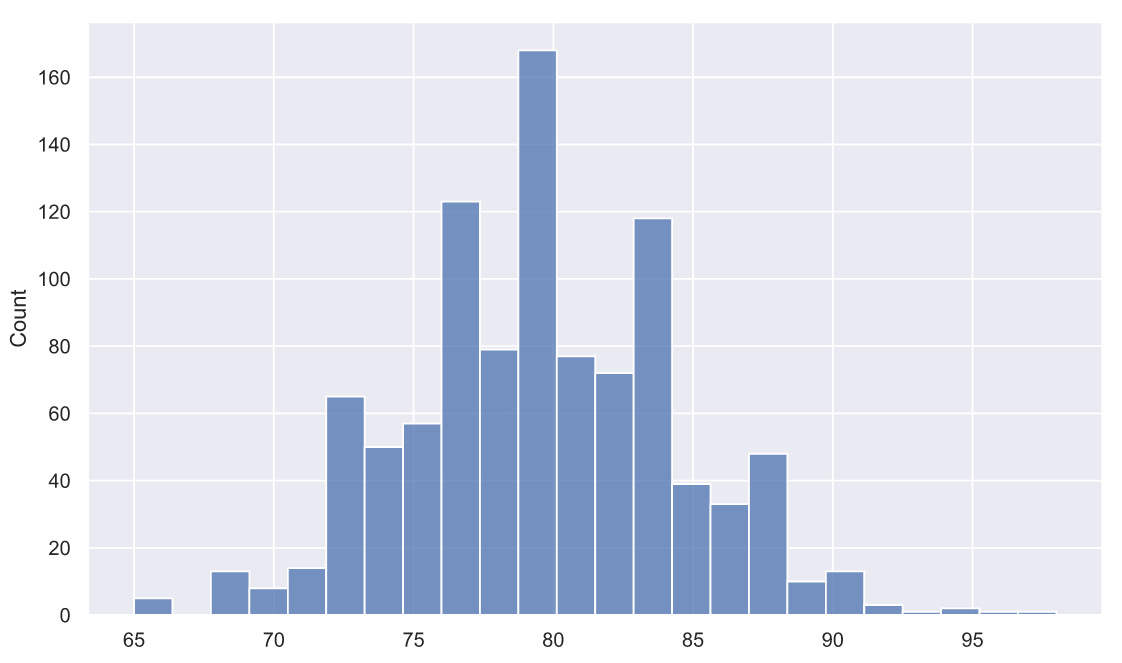

В данном случае, мы можем предположить, что оценки распределены нормально с мат. ожиданием и стандартным отклонением 80 и 5 баллов соответственно. Такой результат означает, что массовый потребитель, конечно же, не считает наше пиво лучшим в мире, но в среднем, видит его где-то в числе лучших.

Все могло бы быть ровно да гладко, особенно в нашем воображении. Но теперь давайте представим, что случилась внезапная неприятность - поставщик хмеля пострадал от неурожая и нам пришлось срочно покупать сырье у другого производителя. Очевидно, что это как-то скажется на качестве пива, но как? Единственный способ проверить это - сварить небольшую партию с новым хмелем и провести опрос у небольшой группы респондентов. Допустим, в оценке качества нового пива приняли участие всего 10 человек, а их оценки распределились следующим образом:

[89, 99, 93, 84, 79, 61, 82, 81, 87, 82]

Теперь мы можем вычислить Z-статистику по уже известной нам формуле:

Z = \frac{\bar{x} - \mu}{\frac{\sigma}{\sqrt{n}}}

где \bar{x}- это среднее значение для нашей выборки, \muи \sigma среднее значение и стандартное отклонение для генеральной совокупности, а n- размер выборки. Вот среднее нашей выборки:

sample = np.array([89,99,93,84,79,61,82,81,87,82])
sample.mean()
83.7

Вот значение Z-статистики:

z = 10**0.5*(sample.mean()-80)/5
z
2.340085468524603

И еще обязательно вычисляем p-value: 

1 - (stats.norm.cdf(z) - stats.norm.cdf(-z))
0.019279327322753836

Для нас, как для пивоваров, это крайне интересные цифры и вот почему: Z-значение отстоит от 0 более чем на 2 сигмы, т.е. отклонение среднего балла 10 респондентов находится очень далеко от среднего бала генеральной совокупности, а вероятность того, что это отклонение произошло случайно, всего около 0.02. Другими словами, если взять 10 человек из совокупности людей, которые оценивают наше "старое" пиво как N(80, 5^{2}), то вероятность того, что эти 10 человек могут случайно дать среднюю оценку "новому" пиву равную 83.7 баллам составляет всего около 2%. Скорее всего, если мы проведем полномасштабный опрос, то увидим, что потребители не просто не заметят изменения качества пива, а даже отметят его небольшое улучшение. Круто.

Но вот что странно - стандартное отклонение оценок тех самых срочно найденных 10 респондентов в два раза больше, чем то, которым мы оценили всю генеральную совокупность потребителей:

sample.std(ddof=1)
10.055954565441423
Врезка по поводу ddof в std

Стандартное отклонение можно рассматривать либо как параметр \sigma, если речь идет о генеральной совокупности, либо как статистику s, если мы говорим о выборке. Оба значения могут быть вычислены по следующим формулам:

\begin{align*} & \sigma={\sqrt {{\frac {1}{n}}\sum _{i=1}^{n}\left(x_{i}-{\mu}\right)^{2}}} \\ & \\ & s={\sqrt {{\frac {1}{n - 1}}\sum _{i=1}^{n}\left(x_{i}-{\bar {x}}\right)^{2}}} \end{align*}

Как видите, отличия не очень сильные и заключаются только в том, что при расчете \sigmaмы используем мат. ожидание генеральной совокупности - \muи делим на n, а при вычислении sиспользуем среднее значение выборки и делим на n - 1. Зачем делить на n - 1вместо n? Все дело в том, что при расчете отклонения выборки вместо \muиспользуется \bar{x} из-за чего значения sполучаются несколько ниже, чем реальное значение \sigmaдля генеральной совокупности. Поэтому знаменатель n - 1нужен для того, чтобы несколько подправить результат - пододвинуть его чуть поближе к истинному значению.

Для того, чтобы учитывать поправку в методе std() пакета NumPy есть параметр ddof, который по умолчанию равен 0, но если мы применяем std() к небольшой выборке, то необходимо явно указать, что ddof=1. Влияние данного параметра на расчеты может быть очень значимым. Например, если мы возьмем 10000 выборок по 10 элементов из N(80, 5^{2})и построим распределение стандартных отклонений, то увидим, что при ddof=0 пик распределения находится левее реального значения стандартного отклонения. При ddof=1 пик распределения так же расположен левее реального значения, но все-таки ближе к нему, чем при ddof=0:

fig, ax = plt.subplots(nrows=1, ncols=2, figsize = (12, 5))

for i in [0, 1]:
    deviations = np.std(stats.norm.rvs(80, 5, (10000, 10)), axis=1, ddof=i)
    sns.histplot(x=deviations ,stat='probability', ax=ax[i])
    ax[i].vlines(5, 0, 0.06, color='r', lw=2)
    ax[i].set_title('ddof = ' + str(i), fontsize = 15)
    ax[i].set_ylim(0, 0.07)
    ax[i].set_xlim(0, 11)
fig.suptitle(r'$s={\sqrt {{\frac {1}{10 - \mathrm{ddof}}}\sum _{i=1}^{10}\left(x_{i}-{\bar {x}}\right)^{2}}}$',
             fontsize = 20, y=1.15);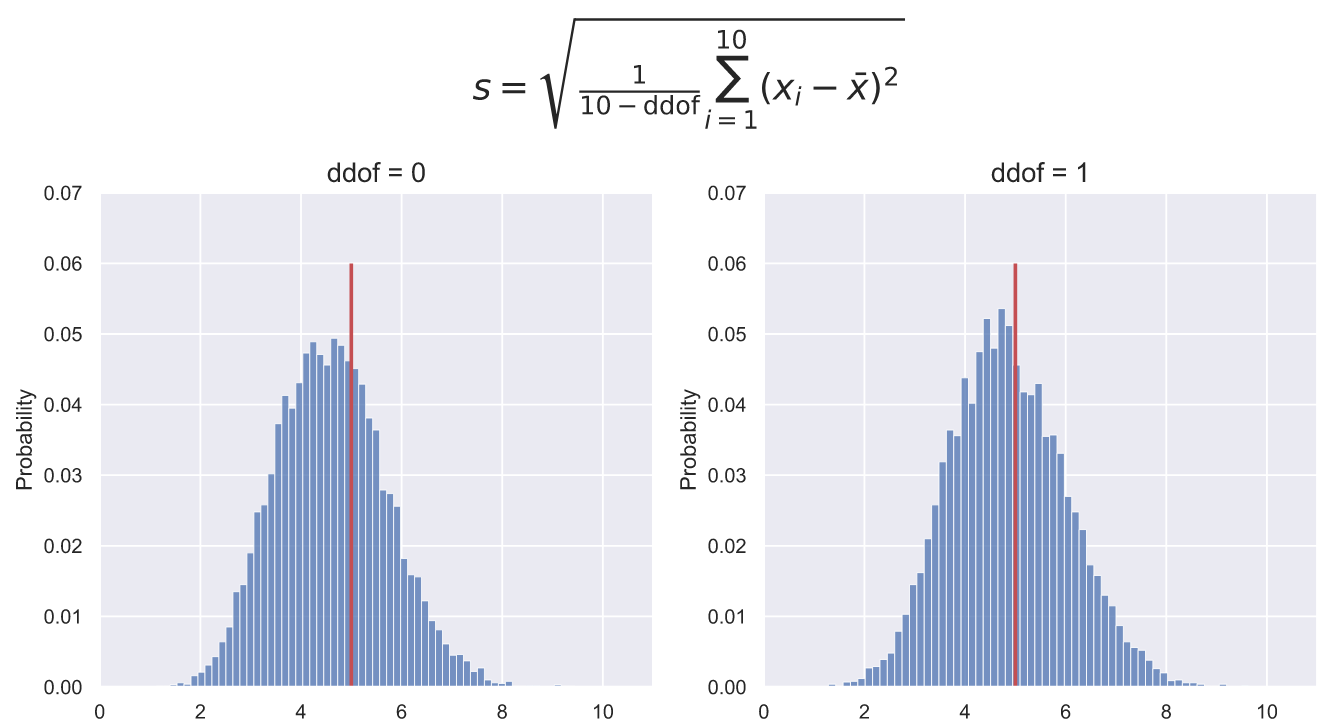

Является ли этот факт важным и можно ли теперь быть уверенными в выводе, который мы сделали на основе Z-статистики? Первое, что приходит в голову - посмотреть, как может быть распределено стандартное отклонение большого количества выборок из генеральной совокупности. Давайте сделаем 5000 тысяч выборок по 10 человек, взятых из распределения N(80, 5) и посмотрим на распределение стандартного отклонения баллов этих выборок:

deviations  = np.std(stats.norm.rvs(80, 5, (5000, 10)), axis=1, ddof=1)
sns.histplot(x=deviations ,stat='probability');

Это похоже на колокол нормального распределения, но важнее то, что стандартное отклонение выборочных оценок не отклоняется до значения равного 10-и баллам. А это крайне настораживающе. Судите сами, если вероятность того, что отклонение среднего балла наших 10 респондентов от среднего генеральной совокупности составляет всего 2%, то вероятность того, что стандартное отклонение (уж простите за каламбур) может отклониться до значения в 10 баллов стремится к 0. А это означает, что для наших выводов об улучшении качества пива, есть вполне уместное замечание: может быть опрос 10-и респондентов свидетельствует не только об изменении среднего генеральной совокупности, может быть ее стандартное отклонение тоже изменилось.

В конце концов, добавление нового сорта хмеля могло привести к большей специфичности вкуса, следовательно, вызвать большую разнонаправленность в предпочтениях: кому-то этот вкус пива стал нравиться больше, кому-то меньше, но средняя оценка могла остаться прежней. Например, если генеральная совокупность оценок "нового" пива теперь распределена как N(80, 10^{2}), то Z-статистика и p-value для имеющихся 10-и оценок будет выглядеть не так обнадеживающе:

z = 10**0.5*(sample.mean()-80)/10
p = 1 - (stats.norm.cdf(z) - stats.norm.cdf(-z))
print(f'z = {z:.3}')
print(f'p-value = {p:.4}')
z = 1.17
p-value = 0.242

Оказывается, что для распределения N(80, 5^{2})резульататы оказались значимыми, но как только мы оценили стандартное отклонение генеральной совокупности тем же значением, что и у выборки, т.е. представили, что генеральная совокупность распределена как N(80, 10^{2}), то это очень сильно отразилось на значимости имеющихся оценок. Ведь вероятность получить такое же или даже еще более отклоненное среднее теперь равна не 2%, а почти 25%. Хотя, всего-то заменили \sigmaна s.

В конце концов, не является ли оценка стандартного отклонения генеральной совокупности значением отклонения выборки более разумным решением? Давайте выясним это! Для этого просто сравним то, как могут быть распределены две статистики: (напомню, что параметрами называют характеристики генеральной совокупности, а статистиками - характеристики выборок)

Z = \frac{\bar{x} - \mu}{\frac{\sigma}{\sqrt{n}}} \; ; \;\;\; T = \frac{\bar{x} - \mu}{\frac{s}{\sqrt{n}}}.

По сути мы просто придумали новую T-статистику, которая отличается от Z-статистики только тем, что в знаменателе стоит не \sigmaгенеральной совокупности, а sвыборки. А теперь сделаем 10000 выборок из N(80, {5}^2), вычислим для каждой выборки Z- и T-статистику, а распределение значений изобразим в виде гистограмм:

fig, ax = plt.subplots(nrows=1, ncols=2, figsize = (12, 5))

N = 10000
samples = stats.norm.rvs(80, 5, (N, 10))
statistics = [lambda x: 10**0.5*(np.mean(x, axis=1) - 80)/5,
              lambda x: 10**0.5*(np.mean(x, axis=1) - 80)/np.std(x, axis=1, ddof=1)]
title = 'ZT'
bins = np.linspace(-6, 6, 80, endpoint=True)

for i in range(2):
    values = statistics[i](samples)
    sns.histplot(x=values ,stat='probability', bins=bins, ax=ax[i])
    p = values[(values > -2)&(values < 2)].size/N
    ax[i].set_title('P(-2 < {} < 2) = {:.3}'.format(title[i], p))
    ax[i].set_xlim(-6, 6)
    ax[i].vlines([-2, 2], 0, 0.06, color='r');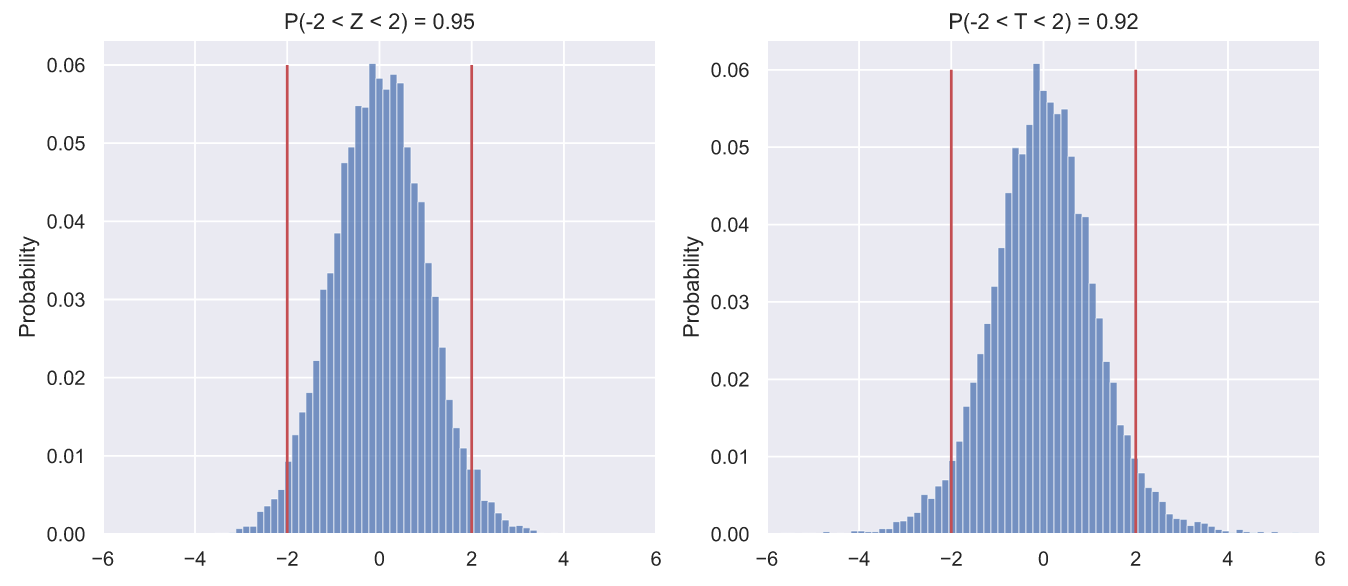

Я все-таки не удержался и сделал гифку:

Код для гифки 
import matplotlib.animation as animation

fig, axes = plt.subplots(nrows=1, ncols=2, figsize = (18, 8))

def animate(i):
    for ax in axes:
        ax.clear()
    N = 10000
    samples = stats.norm.rvs(80, 5, (N, 10))
    statistics = [lambda x: 10**0.5*(np.mean(x, axis=1) - 80)/5,
                  lambda x: 10**0.5*(np.mean(x, axis=1) - 80)/np.std(x, axis=1, ddof=1)]
    title = 'ZT'
    bins = np.linspace(-6, 6, 80, endpoint=True)

    for j in range(2):
        values = statistics[j](samples)
        sns.histplot(x=values ,stat='probability', bins=bins, ax=axes[j])
        p = values[(values > -2)&(values < 2)].size/N
        axes[j].set_title(r'$P(-2\sigma < {} < 2\sigma) = {:.3}$'.format(title[j], p))
        axes[j].set_xlim(-6, 6)
        axes[j].set_ylim(0, 0.07)
        axes[j].vlines([-2, 2], 0, 0.06, color='r')
    return axes

dist_animation = animation.FuncAnimation(fig, 
                                      animate, 
                                      frames=np.arange(7),
                                      interval = 200,
                                      repeat = False)

dist_animation.save('statistics_dist.gif',
                 writer='imagemagick', 
                 fps=1)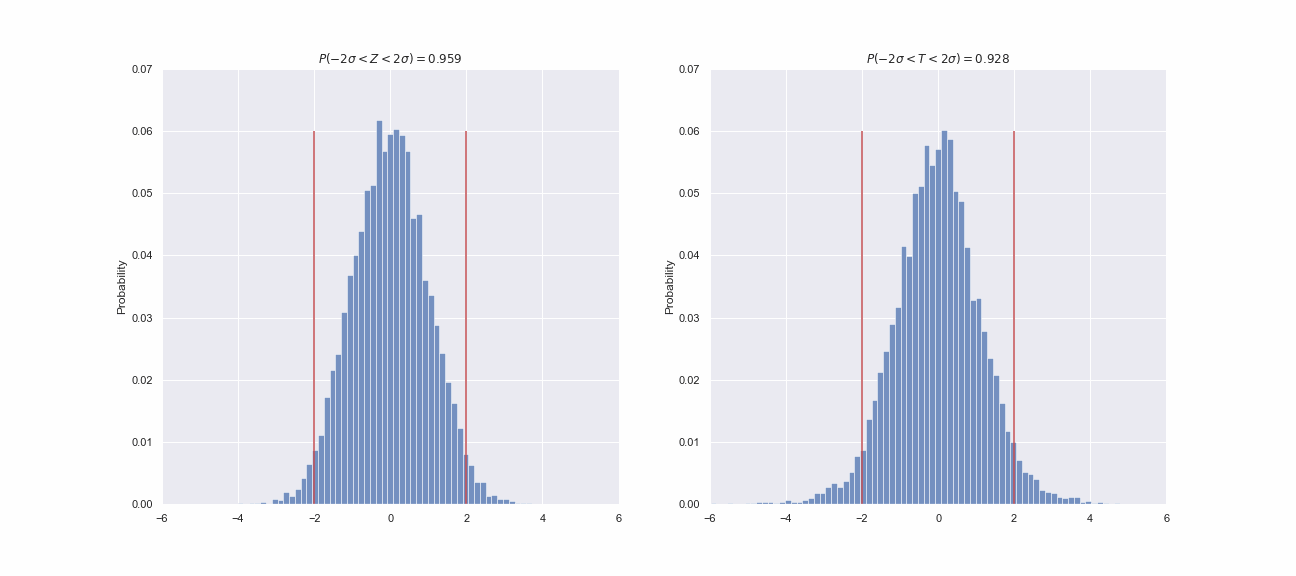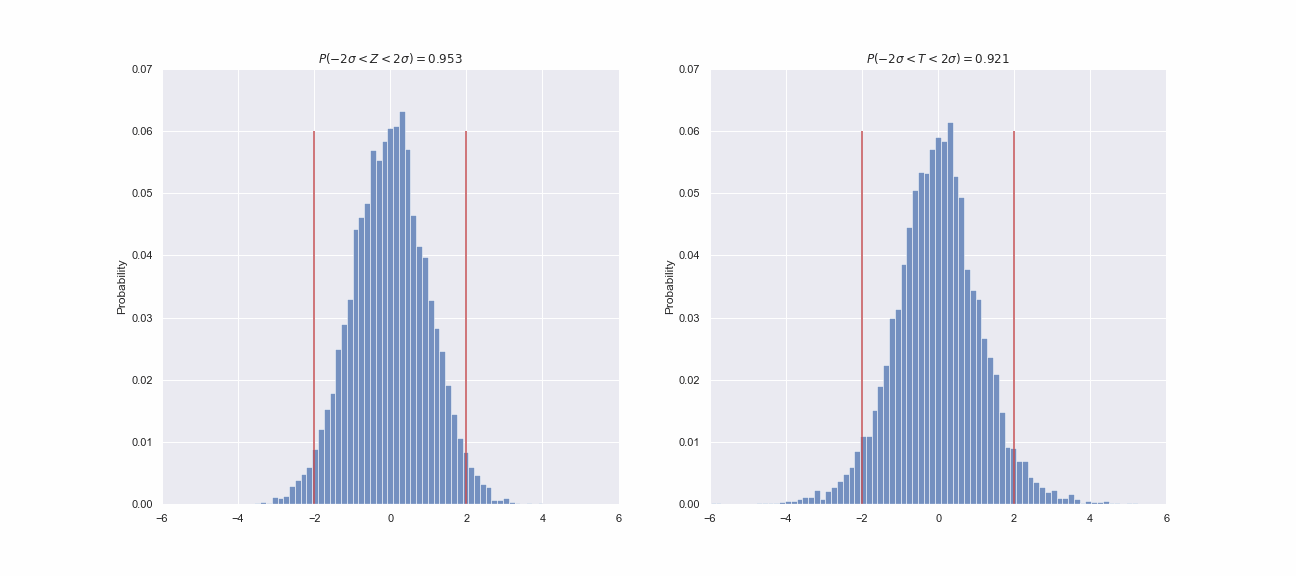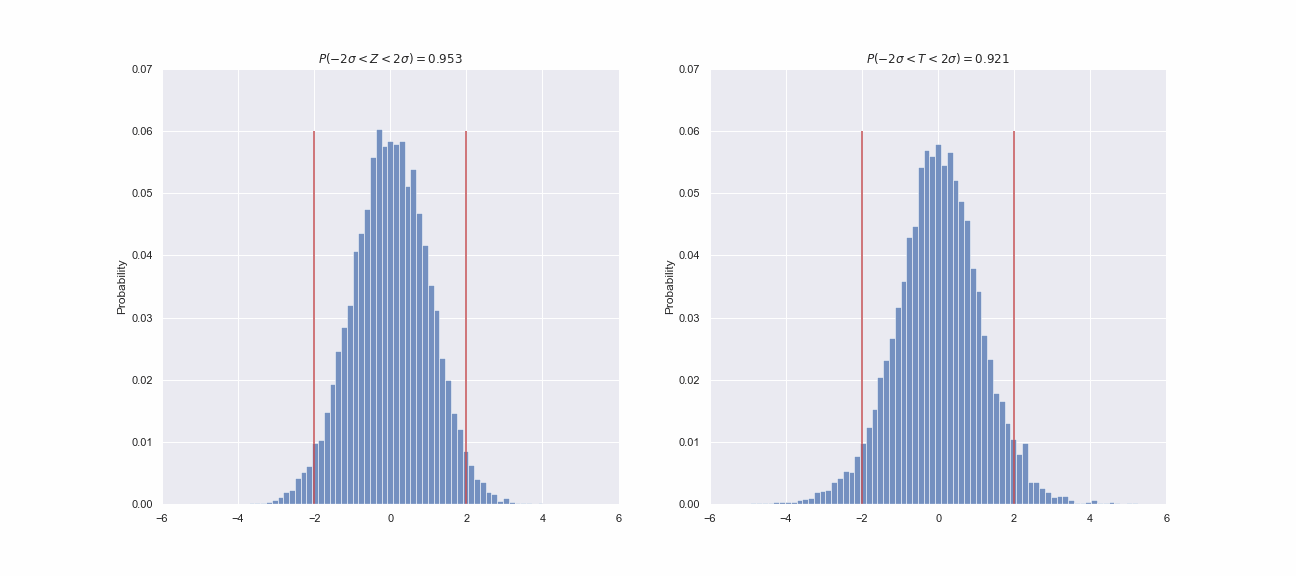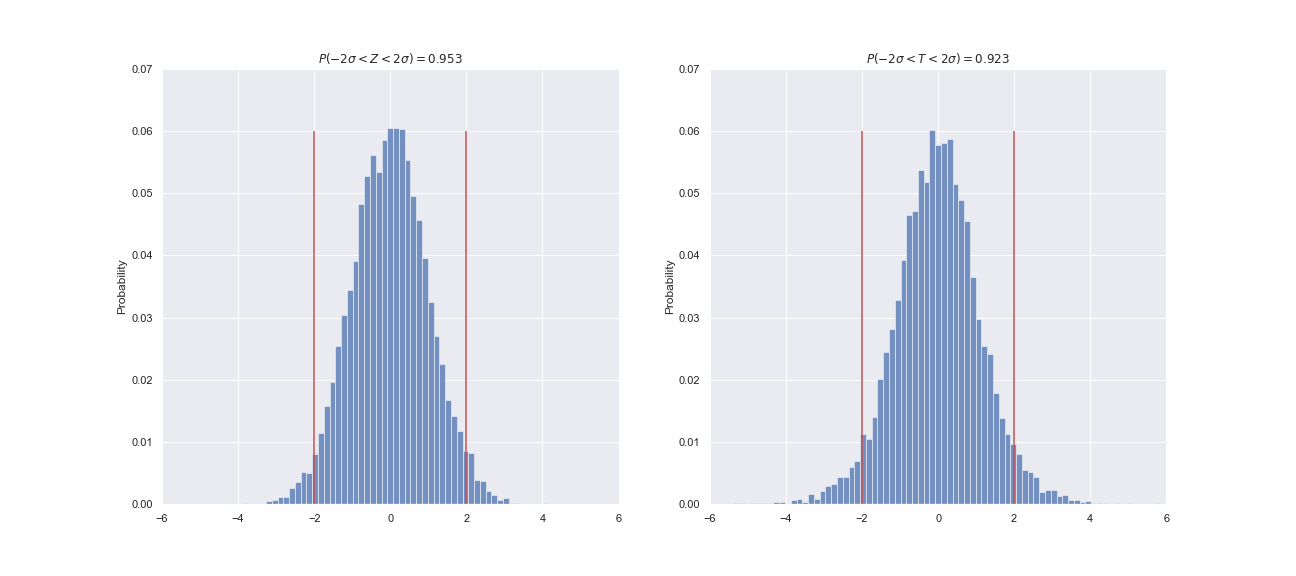

Просто мне кажется, что так можно продемонстрировать, как едва заметные черты могут оказаться чрезвычайно важными для исследователя. На что я хочу обратить ваше внимание? Во-первых, и слева, и справа мы видим свиду два одинаковых колоколообразных распределения. Вполне уместно предположить, что это два стандартных нормальных распределения, верно? Но, вот что любопытно, в N(0, 1)интервал [-2\sigma; 2\sigma]должен содержать около 95.5% всех значений. Для Z-статистики это требование выполняется, а для придуманной нами T-статистики не очень, потому что только 92-93% ее значений укладываются в заданный интервал. Казалось бы, что отличие не столь велико, чтобы заподозрить какую-то закономерность, но мы можем провести больше экспериментов:

statistics = [lambda x: 10**0.5*(np.mean(x, axis=1) - 80)/5,
              lambda x: 10**0.5*(np.mean(x, axis=1) - 80)/np.std(x, axis=1, ddof=1)]

quantity = 50
N=10000
result = []
for i in range(quantity):
    samples = stats.norm.rvs(80, 5, (N, 10))
    Z = statistics[0](samples)
    p_z = Z[(Z > -2)&((Z < 2))].size/N
    T = statistics[1](samples)
    p_t = T[(T > -2)&((T < 2))].size/N
    result.append([p_z, p_t])

result = np.array(result)
fig, ax = plt.subplots()

line1, line2 = ax.plot(np.arange(quantity), result)
ax.legend([line1, line2], 
          [r'$P(-2\sigma < {} < 2\sigma)$'.format(i) for i in 'ZT'])
ax.hlines(result.mean(axis=0), 0, 50, color='0.6');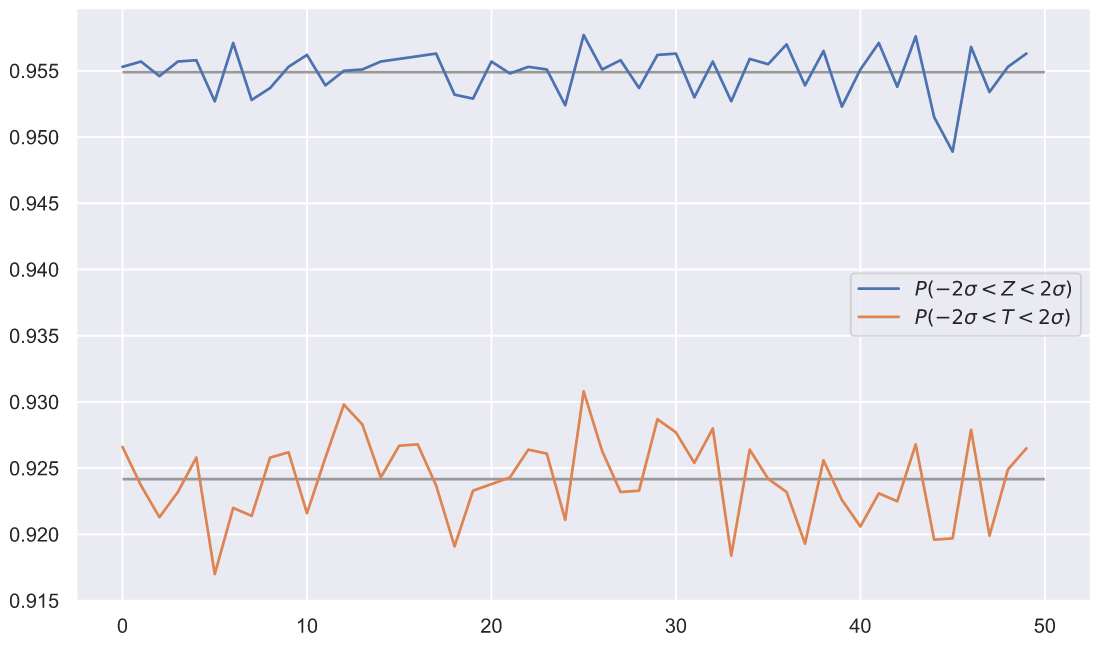

В каждом из 50 экспериментов мы видим одно и тоже. Можно было бы заподозрить, что есть ошибка в коде, но его не так много, и легко убедиться в том, что вычисления выполняются верно. Так в чем же дело? А дело в том, что мы получили совершенно новый тип распределения! Снова взгляните на гифку с гистограммами распределений значений Z- и T- статистик, присмотритесь к основанию колокола каждой из них. Вам не кажется, что у распределения T-статистик основание чуть шире? Это хорошо видно по выпирающим за красные линии, так называемым - хвостам. А то, что эти хвосты несколько больше, или как еще говорят - тяжелее, чем у нормального распределения, так же будет означать, что мы будем наблюдать несколько больше сильных отклонений от вершины распределения. Проще говоря, мы теперь можем учитывать дисперсию выборки при оценке параметров генеральной совокупности. Однако, мы так и не ответили на вопрос - хорошо ли, можно ли, да и вообще зачем оценивать \sigmaгенеральной совокупности значением стандартного отклонения sвыборки.

Задумаемся о дисперсии

Когда мы рассматривали распределение значений Z-статистик, мы обращали внимание только на распределение выборочного среднего \bar{x}и даже не задавались вопросом о том, что выборочное стандартное отклонение s тоже может как-то распределяться. Давайте возьмем 10000 выборок из N(80, 5)по 10 элементов в каждой и посмотрим, как будет выглядеть зависимость стандартного отклонения выборок от их среднего значения:

# если график строиться слишком долго,
# то смените формат svg на png:
#%config InlineBackend.figure_format = 'png'

N = 10000
samples = stats.norm.rvs(80, 5, (N, 10))

means = samples.mean(axis=1)
deviations = samples.std(ddof=1, axis=1)
T = statistics[1](samples)
P = (T > -2)&((T < 2))

fig, ax = plt.subplots()

ax.scatter(means[P], deviations[P], c='b', alpha=0.7,
           label=r'$\left | T \right | < 2\sigma$')
ax.scatter(means[~P], deviations[~P], c='r', alpha=0.7,
           label=r'$\left | T \right | > 2\sigma$')

mean_x = np.linspace(75, 85, 300)
s = np.abs(10**0.5*(mean_x - 80)/2)
ax.plot(mean_x, s, color='k',
        label=r'$\frac{\sqrt{n}(\bar{x}-\mu)}{2}$')
ax.legend(loc = 'upper right', fontsize = 15)
ax.set_title('Зависимость выборочного стандартного отклонения\nот выборочного среднего',
             fontsize=15)
ax.set_xlabel(r'Среднее значение выборки ($\bar{x}$)',
              fontsize=15)
ax.set_ylabel(r'Стандартное отклонение выборки ($s$)',
              fontsize=15);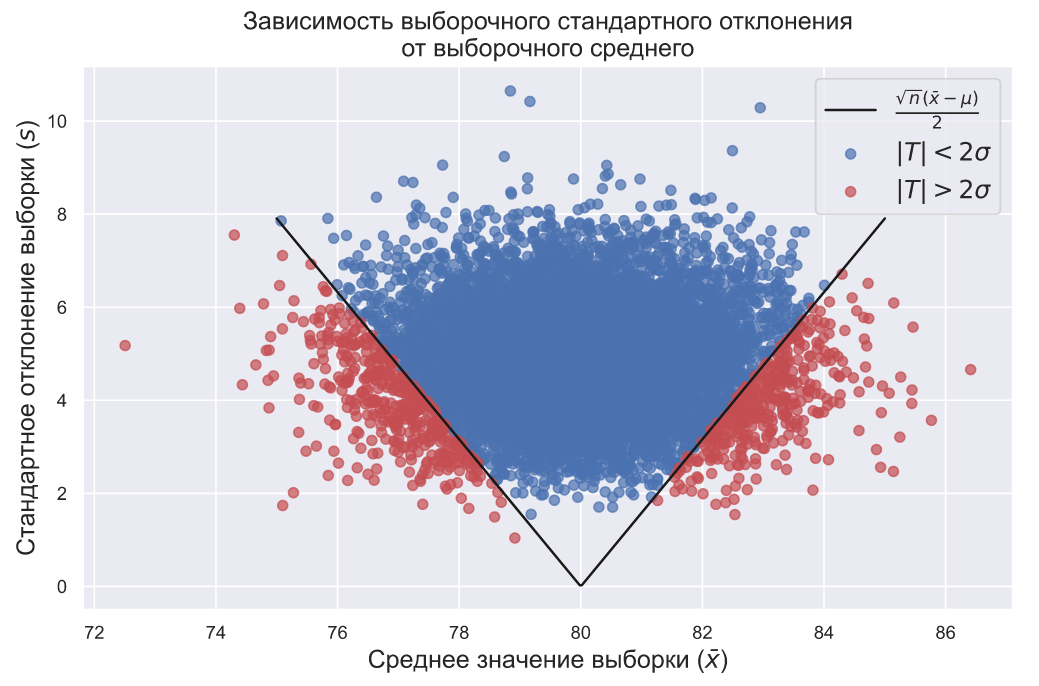

Данный график интересен тем, что показывает зависимость среднего выборки от ее стандартного отклонения. На нем видно, что выборки, у которых \bar{x}и sотклоняется очень сильно и одновременно практически не встречаются, т.е. точки стараются избегать углов графика. Это значит, что, если мы берем выборку из нормального распределения N(\mu, \sigma^{2}), то мы вряд ли увидим слишком большое значение \left | \bar{x} - \mu \right |при большом значении \left | s - \sigma \right |. А еще из данного графика следует, что экстремальные значения (красные точки) могут быть получены, только если выполняется следующее соотношение:

\left | \bar{x} - \mu \right | >\frac{2\sigma s}{\sqrt{n}}

Учитывая, что \sigma=1, т.е. то, что мы снова измеряем расстояние от вершины распределения в сигмах, и то, что для нашего конкретного примера \mu = 80, а n = 10мы можем записать это условие следующим образом:

\left | \bar{x} - 80 \right | >\frac{2s}{\sqrt{10}}

Границы данного условия обозначены на графике черной линией, а поскольку мы раньше уже вычисляли доли значений которые попадали в интервал [-2\sigma; 2\sigma], то мы можем сказать, что над черной линией находится около 92,5% всех точек.

Как интерпретировать это расположение и цвет точек? Давайте вспомним пример, от которого мы отталкивались. Мы сварили пиво с новым сортом хмеля, нашли десять человек (наша выборка) и попросили их оценить качество нового пива по 100-больной шкале. На основании их оценок мы пытаемся понять, как могут оценить качество пива все, кто его купит в дальнейшем (генеральная совокупность). Допустим среднее полученных 10-и оценок равно 82-м баллам, а стандартное отклонение равно всего 2-м баллам. Могут ли такие оценки быть получены случайно, если предположить, что генеральная совокупность имеет мат.ожидание \mu=80, а стандартное отклонение такое же как у выборки, т.е. \sigma = s = 2? Чтобы выяснить это нужно вычислить Z-статистику:

Z = \frac{\bar{x} - \mu}{\frac{\sigma}{\sqrt{n}}} = \frac{82 - 80}{\frac{2}{\sqrt{10}}} \approx 3.16

Чтобы оценить вероятность случайного получения такого значения из N(80, 2^{2})нужно вычислить p-value:

z = 10**0.5*(82-80)/2
p = 1 - (stats.norm.cdf(z) - stats.norm.cdf(-z))
print(f'p-value = {p:.2}')
p-value = 0.0016

Вероятность того что 10 человек случайно дадут средню оценку равную 82-м баллам очень мала и составляет менее 2%. Но данное утверждение является верным только если мы предполагаем что эти десять человек взяты из генеральной совокупности всех потребителей в которой их оценки распределены как N(80, 2^{2}). И если мы действительно предполагаем, что \sigma = s = 2, то мы можем быть вполне уверены, что оценки обусловлены новым сортом хмеля в составе пива, а не случайностью.

Такой результат может наблюдаться, например, в том случае, если мы пригласили экспертов в качестве респондентов. Только эксперты могли бы отметить небольшое улучшение качества пива (малое \left | \bar{x} - \mu \right |) и при этом быть единодушны в оценках (малое s).

С другой стороны мы могли бы пригласить крайне разношерстную публику в качестве 10 респондентов. Они могли бы оценить качество пива так же в 82 балла, но со стандартным отклонением равным, допустим, 9-и баллам. Может ли такая оценка быть получена случайно? Проверим:

z = 10**0.5*(82-80)/9
p = 1 - (stats.norm.cdf(z) - stats.norm.cdf(-z))
print(f'p-value = {p:.2}')
p-value = 0.48

Значит получить случайным образом 10 оценок с результатом \bar{x} = 82и s = 9из распределения N(80, 9^{2})более чем вероятно. Следовательно, мы не можем утверждать, что новый сорт хмеля в составе пива как-то повлиял на изменение мнения генеральной совокупности о его качестве.

Кстати, сейчас вполне уместно поинтересоваться тем, что произойдет если мы будем менять размер выборки. Давайте сделаем вот такую гифку:

Код для гифки
import matplotlib.animation as animation

fig, ax = plt.subplots(figsize = (15, 9))

def animate(i):
    ax.clear()
    N = 10000
    
    samples = stats.norm.rvs(80, 5, (N, i))

    means = samples.mean(axis=1)
    deviations = samples.std(ddof=1, axis=1)
    T = i**0.5*(np.mean(samples, axis=1) - 80)/np.std(samples, axis=1, ddof=1)
    P = (T > -2)&((T < 2))
    
    prob = T[P].size/N
    ax.set_title(r'зависимость $s$ от $\bar{x}$ при $n = $' + r'${}$'.format(i),
                 fontsize = 20)
    ax.scatter(means[P], deviations[P], c='b', alpha=0.7,
               label=r'$\left | T \right | < 2\sigma$')
    ax.scatter(means[~P], deviations[~P], c='r', alpha=0.7,
               label=r'$\left | T \right | > 2\sigma$')

    mean_x = np.linspace(75, 85, 300)
    s = np.abs(i**0.5*(mean_x - 80)/2)
    ax.plot(mean_x, s, color='k',
            label=r'$\frac{\sqrt{n}(\bar{x}-\mu)}{2}$')
    ax.legend(loc = 'upper right', fontsize = 15)
    ax.set_xlim(70, 90)
    ax.set_ylim(0, 10)
    ax.set_xlabel(r'Среднее значение выборки ($\bar{x}$)',
              fontsize='20')
    ax.set_ylabel(r'Стандартное отклонение выборки ($s$)',
              fontsize='20')
    return ax

dist_animation = animation.FuncAnimation(fig, 
                                      animate, 
                                      frames=np.arange(5, 21),
                                      interval = 200,
                                      repeat = False)

dist_animation.save('sigma_rel.gif',
                 writer='imagemagick', 
                 fps=3)

С увеличением элементов в выборке мы наблюдаем, что выборочные \bar{x}и s стремятся к \muи \sigmaраспределения N(\mu, \sigma^{2}),из которого эти выборки были взяты. Так что при больших значениях nмы можем спокойно пользоваться Z-статистиками, зная что при увеличении nстандартные отклонения выборки и генеральной совокупности будут все меньше отличаться друг от друга.

Но постойте! Разве мы не вернулись к тому, с чего начали? Ведь мы снова так и не ответили на вопрос - почему при малых размерах выборки мы предполагаем, что стандартное отклонение генеральной совокупности должно быть таким же, как у выборки. В нашем конкретном примере, с которого все началось, оценки 10-и респондентов выглядели так:

[89,99,93,84,79,61,82,81,87,82]

Среднее этой выборки \bar{x} = 83.7, а стандартное оклонение s = 10.06, причем мы приняли во внимание, что полномасштабный опрос, до введения в состав нового сорта хмеля, показал, что оценки распределены как N(80, 5^{2}). Но вместо Z-статистики, мы решили использовать придуманную T-статистику, единственное отличие которой от Z-статистики состоит в том, что мы просто заменили в формуле \sigmaгенеральной совокупности на sвыборки. По сути мы просто решили проверить гипотезу относительно генеральной совокупности, которая теперь по каким-то причинам распределена не как N(80, 5^{2}), а как N(80, 10.06^{2})- это вообще правильно? Разве не нужно было бы проверить это предположение для самых разных значений s?: Почему мы не предполагаем, что N(80, 1^{2}), N(80, 5^{2}), N(80, 7^{2})или любое другое значение \sigma?

Чтобы ответить на этот вопрос, давайте снова вернемся к изначальному смыслу доказательства гипотез. Суть состоит в том, чтобы на основании выборки из генеральной совокупности сделать какие-то выводы о параметрах распределения этой генеральной совокупности. В нашем примере мы были уверены, что оценки его качества распределены как N(80, 5^{2}), однако, когда мы сварили пиво с новым сортом хмеля, то мы получили 10 оценок, стандартное отклонение которых составило 10 баллов. В самом начале мы видели, что получить выборку с таким отклонением из N(80, 5^{2})просто невозможно. А это значит, что мы просто вынуждены как-то по новому оценить стандартное отклонение генеральной совокупности, иначе все наши выводы не будут иметь никакого отношения к реальности.

Давайте сделаем вот что: среднее нашей выборки \bar{x} = 83.7, а стандартное оклонение s = 10.06, попробуем оценить вероятность получить такую выборку из N(80, \sigma^{2})при разных значениях \sigma. Но поскольку вероятность получить конкретное значение из непрерывного распределения стремится к нулю, то мы оценим вероятность получения выборки, у которой 83<\bar{x}<84и 9.5<s<10.5:

N = 10000
sigma = np.linspace(5, 20, 151)
prob = []

for i in sigma:
    p = []
    for j in range(10):
        samples = stats.norm.rvs(80, i, (N, 10))
        means = samples.mean(axis=1)
        deviations = samples.std(ddof=1, axis=1)
        p_m = means[(means >= 83) & (means <= 84)].size/N
        p_d = deviations[(deviations >= 9.5) & (deviations <= 10.5)].size/N
        p.append(p_m*p_d)
    prob.append(sum(p)/len(p))
prob = np.array(prob)

fig, ax = plt.subplots()
ax.plot(sigma, prob)
ax.set_xlabel(r'Стандартное отклонение генеральной совокупности ($\sigma$)',
              fontsize=20)
ax.set_ylabel('Вероятность',
              fontsize=20);

Как видите, максимум вероятности достигается при \sigma \approx 10. Именно по этой причине, когда мы имеем дело с небольшими выборками, мы проверяем гипотезу о распределении генеральной совокупности не относительно известного нам значения ее стандартного отклонения \sigma, а относительно стандартного отклонения выборки s. Если параметры генеральной совокупности как-то изменились, то мы заранее предполагаем, что ее стандартное отклонение теперь равно стандартному отклонению выборки, просто потому, что вероятность такого изменения максимальна. Вот и все.

А это точно мы изобрели T-статистику?

Давайте представим, что некий инженер в какой-нибудь компании по производству шариков для пинг-понга решил задачу по сверхплотной упаковке шаров. После этого в один грузовой контейнер стало влезать на 1% больше шариков, что в общем-то не густо. Но тем не менее, глава компании мог посчитать этот результат очень важным и запретить инженеру распространять свое решение, так как это решение теперь является коммерческой тайной. Вот так, важный для цивилизации теоретический результат мог бы остаться в тайне ради ничтожного увеличения прибыли какой-то компании по производству шариков для пинг-понга. Абсурд?

Несомненно - абсурд! Однако, что-то подобное чуть не произошло с Уильямом Госсетом, когда он работал на пивоварне "Гиннес" и открыл t-распределение. Оценить практическую значимость некоторых статистических открытий очень сложно, но не в тех случаях, когда на кону астрономические потенциальные прибыли и стратегическое развитие компании, или даже государства. Например, последовательный критерий отношений правдоподобия Вальда, открытый в 1943 году во время войны вообще засекретили, так как этот критерий позволял на 50% уменьшить среднее число наблюдений в выборке. Короче, статистика - это крайне полезная наука.

Итак, Уильям Госсет отвечал за контроль качества в пивоварне "Гиннес" и пытался решить проблему появления ошибок при использовании выборок ограниченного размера. Госсет проделал все то же самое, что мы проделали с вами выше (только без компьютера!) и сделал вывод о том, что если выборка берется из "нормальной" генеральной совокупности и что если использовать стандартное отклонение выборки для оценки стандартного отклонение этой самой генеральной совокупности, то распрделение выборочного среднего можно описать уже знакомой нам формулой:

t = \frac{\bar{x}-\mu}{\frac{s}{\sqrt{n}}}

Данная формула и является формулой так называемого t-распределения, оно же распределение Стьюдента. Учитывая, что история о том, как Госсет использовал псевдоним "Стьюдент", для обхода наложенным Гиннесом запрета на публикации работ, довольно широко известна, то, наверное, было бы правильнее называть это распределение - распределением Госсета. Но названия "распределение Стьюдента", или используемое немного реже "t-распределение" так сильно устоялись, что мы не будем нарушать эту общепринятую договоренность.

Еще один способ получить распределение Стьюдента заключается в использовании вот этой формулы:

t={\frac {Y_{0}}{{\sqrt {{\frac {1}{n}}\sum \limits _{{i=1}}^{n}Y_{i}^{2}}}}},

которая позволяет прояснить понятие "степени свободы" выборки. Пусть случайные переменные Y_{i}берутся из стандартного нормального распределения, т.е. {\displaystyle Y_{i}\sim {\mathcal {N}}(0,1),;i=0,\ldots ,n}, тогда значение n, т.е. объем выборки, как раз и определяет степень свободы распределения Стьюдента. А принадлежность какой-нибудь случайной величины к распределению Стьюдента с определенным числом степеней свободы обозначается, как:

t\sim {\mathrm {t}}(n)

Давайте попробуем взглянуть на то, как будет меняться распределение Стьюдента при увеличении числа степеней свободы:

Код для гифки
import matplotlib.animation as animation

fig, ax = plt.subplots(figsize = (15, 9))

def animate(i):
    ax.clear()
    N = 15000
    
    x = np.linspace(-5, 5, 100)
    ax.plot(x, stats.norm.pdf(x, 0, 1), color='r')
    
    samples = stats.norm.rvs(0, 1, (N, i))
    
    t = samples[:, 0]/np.sqrt(np.mean(samples[:, 1:]**2, axis=1))
    t = t[(t>-5)&(t<5)]
    sns.histplot(x=t, bins=np.linspace(-5, 5, 100), stat='density', ax=ax)
    
    ax.set_title(r'Форма распределения $t(n)$ при n = ' + str(i), fontsize = 20)
    ax.set_xlim(-5, 5)
    ax.set_ylim(0, 0.5)
    return ax

dist_animation = animation.FuncAnimation(fig, 
                                      animate, 
                                      frames=np.arange(2, 21),
                                      interval = 200,
                                      repeat = False)

dist_animation.save('t_rel_of_df.gif',
                 writer='imagemagick', 
                 fps=3)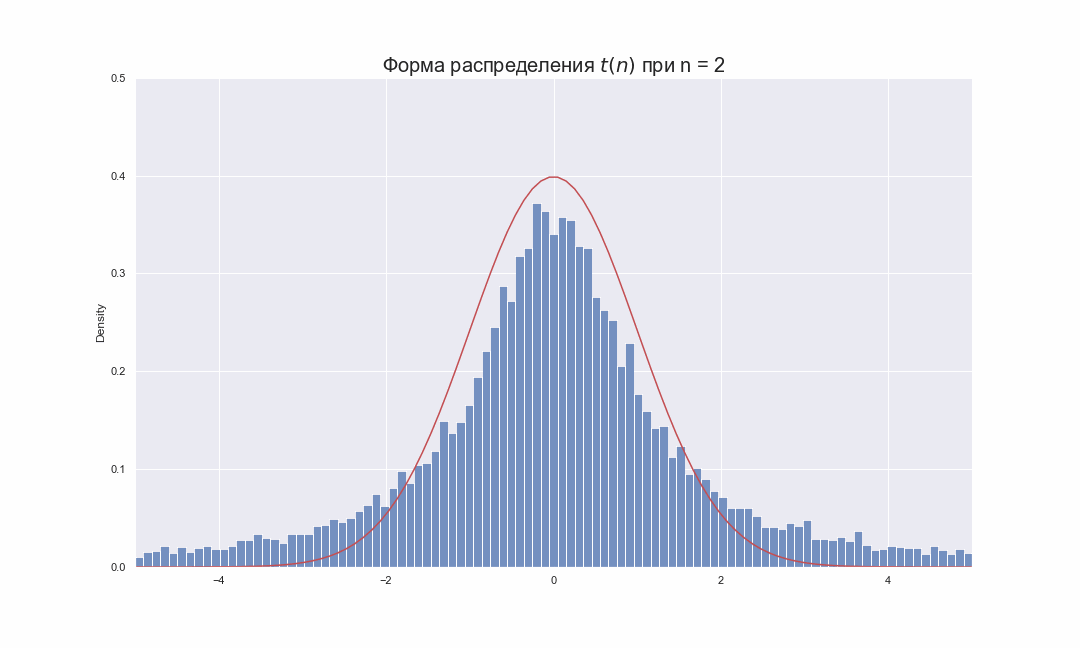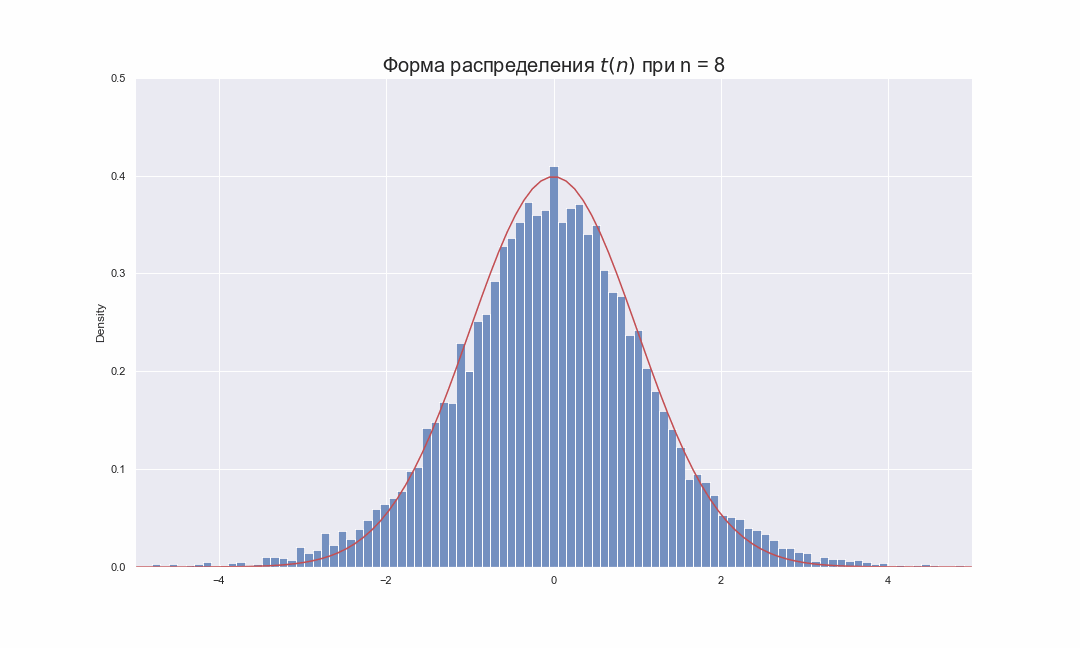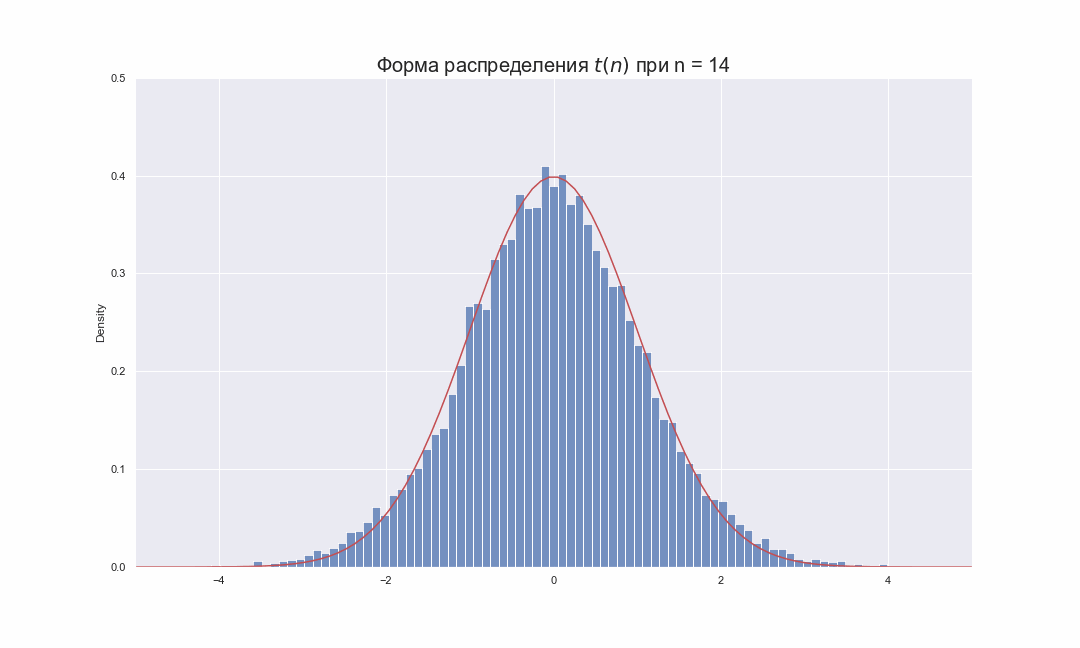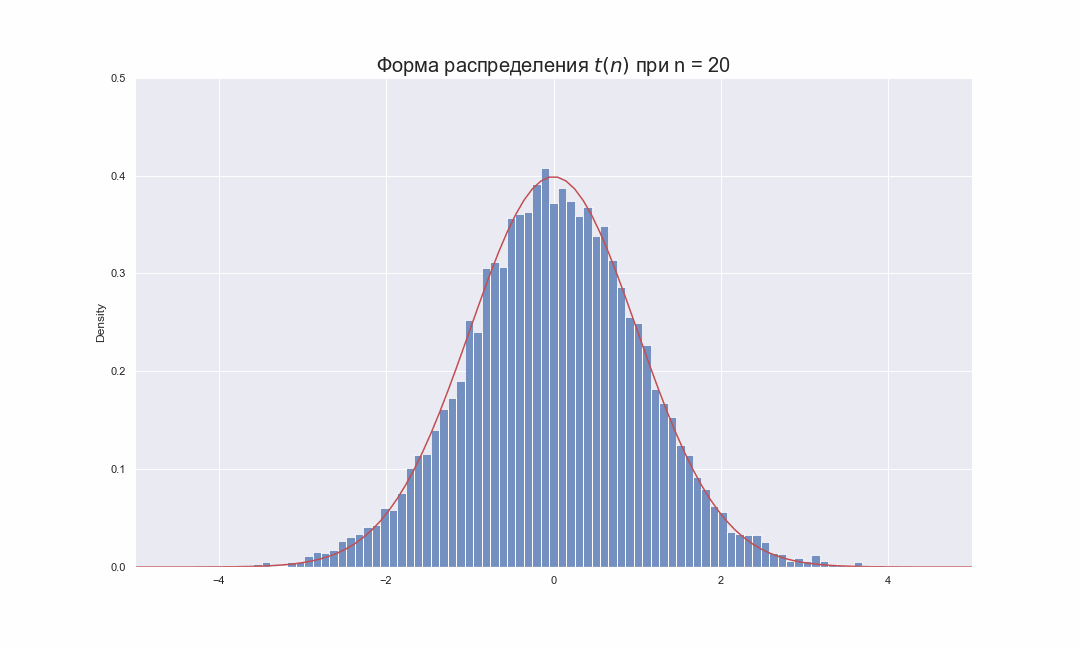

На этой гифке видно, как по мере увеличения n, гистограмма распределения Стьюдента подбирает свои хвосты, стараясь занять всю площадь под красной линией, которая соответствует функции распределения плотности вероятности N(0, 1). Чтобы увидеть это более наглядно, распределение Стьюдента лучше так же изображать в виде линий функций плотности вероятности, которые можно вычислить по следующей формуле:

{\displaystyle f_{t}(y)={\frac {\Gamma \left({\frac {n+1}{2}}\right)}{{\sqrt {n\pi }}\,\Gamma \left({\frac {n}{2}}\right)}}\,\left(1+{\frac {y^{2}}{n}}\right)^{-{\frac {n+1}{2}}}}

Но лучше воспользуемся готовой реализацией в SciPy:

Код для гифки
import matplotlib.animation as animation

fig, ax = plt.subplots(figsize = (15, 9))

def animate(i):
    ax.clear()
    N = 15000
    
    x = np.linspace(-5, 5, 100)
    ax.plot(x, stats.norm.pdf(x, 0, 1), color='r')
    ax.plot(x, stats.t.pdf(x, df=i))
    
    ax.set_title(r'Форма распределения $t(n)$ при n = ' + str(i), fontsize = 20)
    ax.set_xlim(-5, 5)
    ax.set_ylim(0, 0.45)
    return ax

dist_animation = animation.FuncAnimation(fig, 
                                      animate, 
                                      frames=np.arange(2, 21),
                                      interval = 200,
                                      repeat = False)

dist_animation.save('t_pdf_rel_of_df.gif',
                 writer='imagemagick', 
                 fps=3)

Здесь гораздо лучше видно, что при увеличении n(параметр df в коде) распределение Стьюдента стремится к нормальному распределению. Что в общем-то и неудивительно, так как ранее мы уже видели, что при увеличении nвыборки, ее стандартное отклонение все меньше колеблется вокруг стандартного отклонения генеральной совокупности.

t-распределение на практике

Давайте сразу выполним t-тест из модуля SciPy для выборки из нашего примера с пивом:

sample = np.array([89,99,93,84,79,61,82,81,87,82])

stats.ttest_1samp(sample, 80)
Ttest_1sampResult(statistic=1.163532240174695, pvalue=0.2745321678073461)

А теперь попробуем получить тот же самый результат самостоятельно:

T = 9**0.5*(sample.mean() -80)/sample.std()
T
1.163532240174695

Обратите внимание, что при вычислении мы использовали не размер выборки n = 10, а количество степеней свободы df, которое вычисляется как n - 1. Да, количество степеней свободы распределения Стьюдента на 1 меньше объема выборки, а связано это, как вы уже догадались, с разницей в вычислениях стандартного отклонения для выборки и генеральной совокупности. Добиться такого же результата мы можем и так:

T = 10**0.5*(sample.mean() -80)/sample.std(ddof=1)
T
1.1635322401746953

Хорошо, значение t-статистики мы вычислили, как вычислить значение p-value? Думаю, вы и до этого уже догадались - нужно проделать все то же самое, что мы делали при вычислении p-value для Z-статистики, но только с использованием t-распределения:

t = stats.t(df=9)
fig, ax = plt.subplots()
x = np.linspace(t.ppf(0.001), t.ppf(0.999), 300)
ax.plot(x, t.pdf(x))
ax.hlines(0, x.min(), x.max(), lw=1, color='k')
ax.vlines([-T, T], 0, 0.4, color='g', lw=2)
x_le_T, x_ge_T = x[x<-T], x[x>T]
ax.fill_between(x_le_T, t.pdf(x_le_T), np.zeros(len(x_le_T)), alpha=0.3, color='b')
ax.fill_between(x_ge_T, t.pdf(x_ge_T), np.zeros(len(x_ge_T)), alpha=0.3, color='b')

p = 1 - (t.cdf(T) - t.cdf(-T))
ax.set_title(r'$P(\left | T \right | \geqslant {:.3}) = {:.3}$'.format(T, p));

Мы видим, что p-value чуть больше 27%, т.е. вероятность того, что результат получен случайно - довольно велика, особенно в соответствии с самым распространенным уровнем значимости \alpha = 0.05, который меньше p-value более, чем в 5 раз. Что ж, наши результаты не являются значимыми, но они пригодны для демонстрации вычисления доверительного интервала - границы значений математического ожидания генеральной совокупности, в пределах которых оно находится с заданной вероятностью \alpha, обычно равной 0.95:

\textrm{CI}_{1 - \alpha} = \bar{x} \pm \left ( t_{\frac{\alpha}{2}, \textrm{df}} \right )\left ( \frac{s}{\sqrt{n}} \right )

Чтобы вычислить данный интервал в SciPy, достаточно воспользоваться методом interval с заданными параметрами loc (смещение) и scale (масштаб) для нашей выборки:

sample_loc = sample.mean()
sample_scale = sample.std(ddof=1)/10**0.5
ci = stats.t.interval(0.95, df=9, loc=sample_loc, scale=sample_scale)
ci
(76.50640345566619, 90.89359654433382)

Учитывая, что \bar{x} = 83.7, то мы можем утверждать, что с вероятностью \alpha = 0.95математическое ожидание генеральной совокупности находится в пределах интервала [76.5; 90.9]. Чем шире доверительный интервал, тем больше вероятность того, что мы получим совсем другое выборочное среднее \bar{x}, если возьмем другую выборку такого же объема из генеральной совокупности.

Напоследок

Что ж, прошу прощения, друзья, но продолжать и улучшать статью больше нет никаких сил (аврал выбил из колеи). Надеюсь, этого материала будет достаточно, чтобы вы самостоятельно смогли заглянуть под капот t-критерия для независимых выборок, t-критерия для парных измерений, а так же t-критерия для выборок с неравной дисперсией.

Конечно, хотелось бы в конце вставить какую-нибудь гифку, но хочу закончить фразой Герберта Спенсера: "Величайшая цель образования - не знание, а действие", так что запускайте свои анаконды и действуйте! Особенно это касается самоучек, вроде меня.

Жму F5 и жду ваших комментариев!