Способы хранения деревьев в реляционных базах данных c использованием ORM Hibernate / forpes.ru

Главная
Способы хранения деревьев в реляционных базах данных c использованием ORM Hibernate

Способы хранения деревьев в реляционных базах данных c использованием ORM Hibernate +9

07.06.2021 13:35

Ivan_Yuriev 3 4400 Источник

Здравствуйте! В этой статье, я постараюсь кратко рассказать о четырёх достаточно известных способах хранения деревьев с указанием преимуществ и недостатков. На идею написать подобную статью подтолкнул не раз слышимый мною вопрос: "А как это будет в Hibernate?", то есть как реализовать какой-либо из способов хранения дерева с использованием ORM Hibernate. Сразу замечу, что данная статья не является каким-либо призывом использовать именно реляционные БД для решения задач связанных с деревьями, так как понятно что они не заточены конкретно для целей хранения\обработки таких данных. Для иерархии подходят и используются графовые базы данных. Поэтому эта статья будет полезная тем, кому необходимо по каким-либо причинам реализовать хранение дерева именно в реляционной БД. Необходимо также отметить, что и ORM Hibernate также не содержит каких-либо готовых методов из коробки для хранения\обработки деревьев по крайней мере на данный момент, поэтому реализация практически полностью ложиться на плечи разработчика. В примерах далее для понимания полной и целостной картины, кроме сущностей(entity), рассмотрим кратко и такие базовые операции, как получение всех потомков с уровнем вложенности, получение всех родителей с уровнем вложенности, а также операции добавления, удаления и перемещения узла в дереве. В качестве примера дерева послужит структура папок на файловой системе, которая будет отражена в таблицах(е) БД. На такие моменты, как инициализация сущности(entity) не будем акцентировать внимание, полагаю что рассматривать это не имеет смысла, так как алгоритмы обхода дерева известны и описаны во многих книгах и публикациях и будут мало кому интересны. В любом случае мои реализации обхода дерева представлены на GitHub и с ними при желании можно ознакомиться.

Уровень вложенности у меня в SQL запросах будет вычисляемым значением, то есть в таблице(ах) не будет представлена эта величина. Но это не значит, что такой вариант хорош или плох, всё зависит от выбранного способа представления дерева и от вида и частоты совершаемых операций (перемещение, удаление и т.д.) над деревом. Возможно в каком-то конкретно случае будет более эффективно хранить в таблице уровень вложенности и пересчитывать его при перемещении, удалении или добавлении узла в дерево. А возможен и третий вариант, когда исходя из задачи уровень вложенности вообще не нужен, тогда отпадает какая-либо надобность в вычислении и хранении этого значения.

1. Список смежности (Adjacency List)

Идея структуры данных данного представления заключается в том, что каждая вершина дерева хранит информацию о своём непосредственном родителе, то есть в строке таблицы TREE имеется дополнительное поле PARENT_ID, в котором указывается ID родительского узла.

Способ представления дерева в виде списка смежности показан на рисунке выше, опишем кратко важные детали таблицы TREE:

каждый узел в таблице TREE содержит следующую информацию: NAME - имя узла, ID - идентификатор узла, PARENT_ID - идентификатор непосредственного родителя;
родительский идентификатор PARENT_ID является внешним ключом, который ссылается на первичный ключ ID в этой же таблице;
узлы с родительским идентификатором PARENT_ID=null – корневые.

Пример:

В таблице TREE у узла F c ID=6, есть внешний ключ PARENT_ID=5, который ссылается на первичный ключ с таким же значением ID=5 и соответствует узлу с именем С, что и подтверждает граф слева на рисунке: узел C является родителем узлу F. В свою очередь узел F является родителем для узлов H и K, так как у обоих PARENT_ID = 6.

1.1. Сущность (Entity) для Adjacency List

@Entity
@Table(name = "tree")
@DynamicUpdate
public class Node implements Serializable {

    @Id
    @GeneratedValue(strategy = GenerationType.IDENTITY)
    private long id;

    @ManyToOne(fetch = FetchType.LAZY)
    @JoinColumn(name="parent_id", foreignKey=@ForeignKey(name = "FK_PARENT_ID"))
    private Node parent;

    @NotNull
    private String name;

    @OneToMany(fetch = FetchType.LAZY, cascade = CascadeType.ALL)
    @JoinColumn(name = "parent_id")
    @OnDelete(action = OnDeleteAction.CASCADE)
    private List<Node> children = new ArrayList<>();
  
  //default constructor
  // getters
  // setters
  ...
}

Краткое описание сущности (только важное)

Если приглядеться, то сущность Node имеет сходство со структурным шаблоном проектирования Компоновщик (англ. Composite pattern), который и используется для объединения объектов в древовидную структуру и представления в виде иерархии. Поэтому entity Node позволяет аналогичным образом, как и паттерн Компоновщик произвести обход всех узлов дерева с целью получить всех родителей или потомков, что может подтолкнуть, так и сделать. Но стоит сразу предупредить, что такой подход будет не эффективен, как с точки зрения производительности, так и с точки зрения количества отправленных SQL запросов в БД. Более эффективным будет использование рекурсивных SQL запросов, либо хранимых процедур, которые позволят одним запросом или вызовом в случае процедуры получить список всех потомков или родителей. В примерах далее, я ограничусь использованием рекурсивных SQL запросов, которые будут работать во всех базах данных поддерживающих стандарт SQL 1999. Также стоит отметить, что entity Node имеет два вида связи OneToMany (один ко многому) и ManyToOne (много к одному), что даёт возможность как получать список потомков (только 1-го уровня вложенности) со стороны родителя, так и со стороны потомка получить непосредственного родителя. В сущности Node используется каскадирование (cascade), которое позволяет применить изменения состояния экземпляра сущности на все с ней связанные экземпляры сущностей при переходе из временного состояния в хранимое.

Далее приведём конкретные примеры базовых операций над деревом и уже в ходе рассмотрения будем более подробно останавливаться на некоторых моментах сущности Node и возможностей, которые предоставляет ORM Hibernate.

1.2. Получение всех потомков

Для получения потомков первого уровня вложенности можно обойтись без рекурсивного запроса, достаточно буде вызвать метод getChildren() сущности Node, а ORM Hibernate сгенерирует простой запрос, который представлен ниже.

select
    children0_.parent_id as parent_i3_0_0_,
    children0_.id as id1_0_0_,
    children0_.id as id1_0_1_,
    children0_.name as name2_0_1_,
    children0_.parent_id as parent_i3_0_1_ 
from
    tree children0_ 
where
    children0_.parent_id=?

Для получения потомком всех уровней вложенности - потребуется уже рекурсивный запрос. Ниже представлен пример рекурсивного запроса.

<named-native-query name="getAllСhildren" result-set-mapping="NodeWithLevelMapping">
    <query>
        <![CDATA[         
        WITH RECURSIVE r (id, parent_id, name, level) AS
        -- Initial Subquery
        (SELECT id, parent_id, name, 1
        FROM tree
        WHERE parent_id = :id
        UNION ALL
        -- Recursive Subquery
        SELECT t.id, t.parent_id, t.name, r.level + 1
        FROM r INNER JOIN tree t
        ON r.id = t.parent_id)
        -- Result Query
        SELECT * FROM r
        ]]>
    </query>
    <hint name="org.hibernate.comment" value="Get Сhildren By ID"/>
</named-native-query>

Приведённый выше запрос - это пример именованного рекурсивного SQL запроса. Hibernate позволяет хранить запросы, как в метаданных XML, так и в виде аннотаций @NamedQuery и @NamedNativeQuery. Имя запроса в данном случае "getAllСhildren" является его уникальным идентификатором по которому осуществляется обращение. Так как запрос большой и к тому же у меня он не один, я предпочёл использовать хранение именованных запросов в отдельном XML файле. К именованным запросам, я ещё добавляю комментарий, который логируется вместе с запросом, что упрощает дальнейший анализ информации.

Перейдём к телу запроса и кратко опишем.

Тело запроса состоит из инициализирующей части и рекурсивной. Инициализирующая часть содержит простой запрос для получения потомков первого уровня вложенности для узла с конкретным идентификатором id, который передаётся в запрос как параметр. Дополнительно в список возвращаемых столбцов добавлен уровень вложенности (level) с начальным значением 1. Рекурсивная же часть содержит запрос, который возвращает с каждой итерацией потомков следующего уровня. Последний запрос SELECT * FROM r вернёт нам результат рекурсии. В итоге получим список всех потомков с уровнем вложенности.

1.3. Получение всех родителей

Для получения непосредственного родителя аналогично, как и для получения потомков первого уровня не требуется использование рекурсивного запроса, достаточно будет вызвать метод getParent() сущности Node, а фреймворк уже сгенерирует простой запрос для получения родителя.

select
    node0_.id as id1_0_0_,
    node0_.name as name2_0_0_,
    node0_.parent_id as parent_i3_0_0_,
    node1_.id as id1_0_1_,
    node1_.name as name2_0_1_,
    node1_.parent_id as parent_i3_0_1_ 
from
    tree node0_ 
left outer join
    tree node1_ 
        on node0_.parent_id=node1_.id 
where
    node0_.id=?

Для получения же всей иерархии родителей с уровнем вложенности потребуется рекурсивный запрос, который представлен ниже.

<named-native-query name="getAllParents" result-set-mapping="NodeWithLevelMapping">
    <query> 
        <![CDATA[        
        WITH RECURSIVE r(id, name, parent_id, level) AS
        -- Initial Subquery
        (SELECT tr.id, tr.name, tr.parent_id, 1
        FROM tree tl
        LEFT JOIN tree tr 
        ON tl.parent_id = tr.id
        WHERE tl.id = :id
        UNION ALL
        -- Recursive Subquery
        SELECT t.id, t.name, t.parent_id, level+1
        FROM tree t, r
        WHERE t.id = r.parent_id )
        -- Result Query
        SELECT id, name, parent_id, (SELECT max(level) FROM r) - level + 1 AS level
        FROM r
        ]]>
    </query>
    <hint name="org.hibernate.comment" value="Get Parents By ID"/>
</named-native-query>

Кратко опишем тело запроса.

Инициализирующая часть содержит запрос для получения ближайшего родителя для конкретного узла, id которого передаётся в запрос в качестве параметра. В рекурсивной части находится запрос, который возвращает с каждой итерацией родителя следующего уровня. Так как значение уровня вложенности наращивается в обратном порядке, то уже в последнем результирующем запросе с целью исправить порядок, добавлен такой запрос: (SELECT max(level) FROM r) - level + 1. В итоге получим список всех родителей с уровнем вложенности, где порядок идёт от корневого узла.

1.4. Добавление узла в дерево

Ниже приведён пример метода на языке java позволяющий добавить узел в дерево. Благодаря включенному каскадированию, экземпляр сущности node будет сохранён в БД со всеми связями (вся иерархия) при переходе из временного состояния в хранимое. Под капотом ORM Hibernate сгенерирует все необходимые insert и update запросы для добавления и связывания узлов дерева в таблице БД.

public void add(Node parentNode, Node node) {
    node.setParent(parentNode);
    Session session = HibernateUtil.getSessionFactory().getCurrentSession();
    session.beginTransaction();
    session.save(node);
    session.getTransaction().commit();
}

1.5. Удаление узла из дерева

Удаление узла и его потомков можно осуществить следующими способами:

Каскадное удаление с помощью Hibernate операции session.remove(node).
Удаление с использованием рекурсивного запроса.
Воспользоваться наличием у таблицы TREE внешнего ключа и задать для него в схеме каскадное удаление (ON DELETE CASCADE). И затем использовать простую SQL операция DELETE для узла.

Первый способ удаления будет малоэффективен, так как Hibernate загрузит все связанные узлы потомки, а затем удалит каждый индивидуально. Такой способ неэффективен, как с точки зрения израсходованной памяти, количеству отправленных запросов в БД, так и затраченному на всё это времени. Второй способ получше, так как потребуется всего один запрос, который вычитает узел и всю его иерархию потомков, а затем всё удалит. Третий способ будет наиболее эффективен, так как при удалении узла, все связанные с ним узлы потомки будут удалены автоматически на уровне БД. Как правило, база данных выполняет каскадное удаление более эффективно, чем если произвести подобную операцию на уровне SQL запросов. Приведём в качестве примера третий наиболее эффективный способ.

В сущности Node (см. пункт 1.1.) имеется аннотация @OnDelete(action = OnDeleteAction.CASCADE), которая влияет только на схему генерируемую Hibernate. Если не используется генерируемая Hibernate схема, необходимо убедиться, что включено это ограничение для внешних ключей в вашей схеме. Выглядит данное ограничение (CONSTRAINT) для таблицы tree следующим образом:

CONSTRAINT fk_parent_id FOREIGN KEY (parent_id)
REFERENCES tree (id) MATCH SIMPLE
ON DELETE CASCADE

ON DELETE CASCADE позволяет удалять все связанные ссылки, то есть при удалении узла будут удалены и все его дочерние автоматически на уровне БД. В итоге для рекурсивного удаления
всех зависимых данных потребуется только одна операция DELETE, запрос которой представлен ниже.

<named-query name="delete">
    <query>
       <![CDATA[
        DELETE FROM Node WHERE id = :id
        ]]>
    </query>
    <hint name="org.hibernate.comment" value="Delete Node By ID"/>
</named-query>

1.6. Перемещение узла в дереве

Ниже приведён пример метода на языке java позволяющий переместить узел в дереве.

public void move(Node parentNode, Node node) {
    node.setParent(parentNode);
    Session session = HibernateUtil.getSessionFactory().getCurrentSession();
    session.beginTransaction();
    session.update(node);
    session.getTransaction().commit();
}

Операция перемещения узла достаточно простая, требуется всего лишь обновить parent_id перемещаемого узла. Hibernate сгенерирует в итоге следующий простенький запрос:

UPDATE tree
SET parent_id=?
WHERE id=?

1.7. Преимущества и недостатки

Преимущества:

ссылочная целостность данных;
простая операция удаление узла со всеми его потомками благодаря ссылочной целостности (ON DELETE CASCADE);
простая операция перемещения узла в дереве (достаточно обновить только одно поле parent_id у перемещаемого узла);
простая операция добавление узла в дерево (необходимо добавить узел с потомками в таблицу и обновить parent_id);
простота получения потомков 1-го уровня вложенности;
простота получения непосредственного родителя.

Недостатки:

получение всех потомков узла;
получение всех родителей узла.

Сложность обусловлена тем, что для получения родителей или потомков всех уровней вложенности потребуется совершить множество итераций используя для этих целей рекурсивный запрос или хранимую процедуру. Каждая же итерация – это переход по дереву вниз (получение потомков), или вверх (получение родителей), в зависимости от условия связи.

К недостаткам или даже неудобствам ещё можно отнести и то, что пока ещё встречаются БД, которые не поддерживают рекурсивные запросы (пример: Apache Derby 10.15.2.0), хотя и в этом случае остаётся возможность использовать хранимые процедуры.

2. Таблица связей (Closure Table)

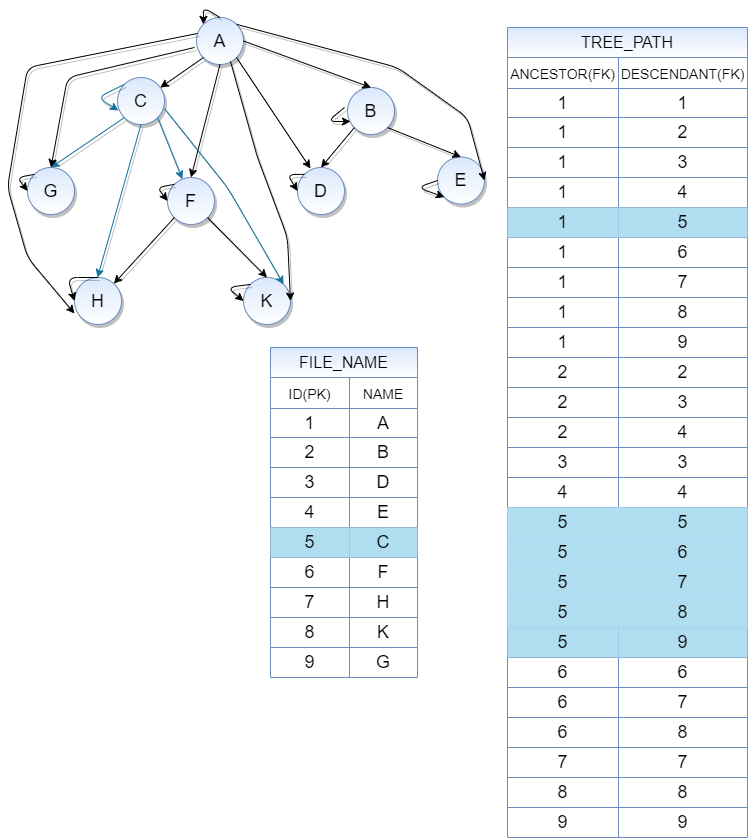
Способ представления дерева в виде таблицы связей показан на рисунке выше, опишем кратко важные детали таблиц FILE_NAME и TREE_PATH.

Таблица FILE_NAME содержит:

ID - идентификатор узла (первичный ключ);

NAME - имя узла.

Таблица TREE_PATH содержит:

ANCESTOR - идентификатор родительского узла (внешний ключ);
DESCENDANT - идентификатор узла потомка (внешний ключ).

Оба внешних ключа ANCESTOR, DESCENDANT ссылаются на первичный ключ ID в таблице FILE_NAME.

Кратко об идеи "Closure Table"

Идея структуры данных данного представления заключается в том, что связи между узлами дерева хранятся в отдельной таблице TREE_PATH, а в основной таблице FILE_NAME содержится только перечень (имена и идентификаторы) всех узлов из которых состоит дерево. Таблица TREE_PATH хранит связи каждого узла дерева со всеми его предками, а так же ссылку каждого узла на самого себя. По иллюстрации "Closure Table" можно заметить и один из недостатков данного способа представления - это большое количество записей в таблице TREE_PATH, которые необходимы для описания всех связей. Чем глубже в дереве находится узел, тем больше потребуется записей для описания связей. В то же время данный способ даёт возможность получить всех родителей или потомков одним простым запросом не прибегая к рекурсии.

Пример:

В основной таблице FILE_NAME узел С имеет ID=5. Переместимся в таблицу связей TREE_PATH и выберем все записи с ANCESTOR = 5 и как результат, получим список всех потомков с такими значениями DESCENDANT: 5, 6, 7, 8, 9 (на рисунке подкрашены синим цветом). Значение DESCENDANT равное 5 - это ссылка узла на самого себя, а уже 6, 7, 8, 9 - это потомки ID которых соответствует именам F, H, K, G, что и показано на рисунке графа.

Теперь выберем из таблицы связей TREE_PATH все записи, где DESCENDANT = 5, как результат получим список всех родителей для узла С. В данном конкретном случае получим одну запись с ANCESTOR = 1, что соответствует узлу с именем A. Всё отвечает тому, что изображено на рисунке с графом узел A является родителем для узла C.

2.1. Сущность FileName

@Entity
@Table(name = "file_name")
@DynamicUpdate
public class FileName implements Serializable {

    @Id
    @GeneratedValue(strategy = GenerationType.IDENTITY)
    private long id;
    @NotNull
    private String name;

    @OneToMany(fetch = FetchType.LAZY, cascade = CascadeType.ALL, mappedBy = "descendant")
    @OnDelete(action = OnDeleteAction.CASCADE)
    private List<TreePath> parents = new ArrayList<>();

    @OneToMany(fetch = FetchType.LAZY, cascade = CascadeType.ALL, mappedBy = "ancestor")
    @OnDelete(action = OnDeleteAction.CASCADE)
    private List<TreePath> children = new ArrayList<>();
  
//default constructor
// getters
// setters
  ...
}

Краткое описание сущности (только важное)

В приведённой выше сущности, есть две связи @OneToMany, которые необходимы для получения всех родителей (parents) и всех потомков (children) для конкретного узла. Также нужно упомянуть, что благодаря ссылочной целостности у нас есть возможность использовать каскадное удаление, обновление и сохранение всех связанных экземпляров сущности, что серьёзно упрощает работу. В сущности эта каскадная передача изменений включена cascade = CascadeType.ALL для обеих связей OneToMany: родителей и потомков. А конкретно процесс удаления можно вообще перенести на уровень БД и для этого в сущности добавлены 2 аннотации @OnDelete(action = OnDeleteAction.CASCADE), но здесь важно понимать, что аннотация влияет только на схему, которую генерирует Hibernate.

2.2. Сущность TreePath

@Entity
@Table(name = "tree_path")
@DynamicUpdate
@IdClass(TreePathId.class)
public class TreePath implements Serializable {

    @Id
    @ManyToOne(targetEntity = FileName.class)
    @JoinColumn(name = "ancestor", nullable = false, foreignKey = @ForeignKey(name = "FK_ANCESTOR"))
    private FileName ancestor;

    @Id
    @ManyToOne(targetEntity = FileName.class)
    @JoinColumn(name = "descendant", nullable = false, foreignKey = @ForeignKey(name = "FK_DESCENDANT"))
    private FileName descendant;
  
//default constructor   
// getters
// setters
 ... 
}

Краткое описание сущности (только важное)

Сущность TreePath содержит связь @ManyToOne для родителя (ancestor) и потомка (descendant). Аннотирование @ManyToOne, определяет, что на уровне базы данных множеству записей таблицы TREE_PATH будет соответствовать одна запись из таблицы FILE_NAME. Если простыми словами и в общих чертах применительно к рассматриваемому дереву, то суть этих аннотаций в следующем: у одного родителя может быть множество потомков (см. рисунок "Таблица связей") и у потомка может быть множество родителей, то есть вся иерархия родителей до корневого узла. Аннотация @IdClass(TreePathId.class) в сущности TreePath - это составной ключ, а класс TreePathId содержит перечень столбцов из которых состоит ключ.

2.3. IdClass TreePathId

public class TreePathId implements Serializable {

    private long ancestor;
    private long descendant;
  
//default constructor 
// getters
// setters
  ...
}

Класс TreePathId - это модель составного ключа, который состоит из двух полей ancestor и descendant.

В сгенерированной Hibernate схеме для таблицы TREE_PATH появится CONSTRAINT указывающий на наличие составного ключа, пример представлен ниже.

CONSTRAINT tree_path_pkey PRIMARY KEY (ancestor, descendant)

2.4. Получение всех потомков

В случае, если нет необходимости в определении уровня вложенности для потомков, то достаточно будет вызвать метод getChildren() у сущности FileName. Hibernate сгенерирует подобный запрос, который приведён ниже:

SELECT * 
FROM file_name f
INNER JOIN tree_Path t ON f.id = t.descendant
WHERE t.ancestor=:id

Сразу стоит отметить, что этот запрос вернёт не только весь список потомков, но также будет содержать и родителя (ancestor) для которого вызывался этот запрос. Дело в том, что таблица связей TREE_PATH хранит не только связи каждого узла дерева со всеми его потомками, но ещё и ссылку каждого узла на самого себя. Чтобы исключить ссылку на самого себя, необходимо в запрос добавить ещё одно условие descendant!=ancestor. Запрос будет выглядеть так:

SELECT * 
FROM file_name f
INNER JOIN tree_Path t ON f.id = t.descendant
WHERE t.ancestor=:id AND t.descendant!=t.ancestor

А теперь перейдём к случаю, когда уровень вложенности нужен. На уровне кода подсчитать его для каждого потомка будет неэффективно, как по количеству отправленных запросов в БД, так и затраченному времени. Правда и сам запрос с подсчётом уровня вложенности станет более громоздким, что естественным образом отразиться в какой-то степени и на его скорость выполнения в целом. Ниже приведён пример именованного запрос для получения всех потомков с уровнем вложенности:

<named-native-query name="getAllСhildren" 
                    result-set-mapping="FileNameWithLevelMapping">
    <query>
        <![CDATA[
        -- Result Query
        SELECT p.id, p.name, count(*) - l.level AS level
        FROM tree_Path t,
        -- (1) get the level of a parent node.
        (SELECT count(*) -1 AS level
        FROM tree_path
        WHERE descendant = :id) l,
        -- (2) get all descendants.
        (SELECT * FROM file_name f
        INNER JOIN tree_Path t ON f.id = t.descendant
        WHERE t.ancestor=:id AND t.descendant!=t.ancestor) p

        WHERE p.descendant = t.descendant AND t.descendant!=t.ancestor
        GROUP BY p.id, p.name, l.level
        ]]>
    </query>
    <hint name="org.hibernate.comment" value="Get Сhildren By ID"/>
</named-native-query>

Перейдём к телу запроса и кратко опишем.

Вычисление уровня вложенности осуществляется путём подсчёта количества родителей для каждого потомка. Разобьём запрос условно на части из которых он состоит и опишем. Для описания подзапросы помечены комментарием с номером.

(1) Подзапрос необходим для получения значения уровня вложенности для родительского узла. Это значение вложенности фигурирует в результирующем запросе count(*) - l.level и необходимо, чтобы отсчёт значения вложенности происходил относительно родительского узла, а не корневого.

(2) Подзапрос служит для получения всех потомков узла с идентификатором :id. Этот запрос уже был приведён выше в начале раздела 2.4.

Результирующий запрос соединяет таблицу tree_path и все подзапросы (1), (2) и производит подсчёт количества родителей для каждого потомка. Таким образом достигается подсчёт уровня вложенности относительно родительского узла для всех его потомков.

2.5. Получение всех родителей

Аналогично, как и для получения потомков, если не требуется уровень вложенности, тогда достаточно вызвать метод getParents() у сущности FileName. Hibernate сгенерирует подобный запрос, который приведён ниже:

SELECT *
FROM file_name f
INNER JOIN tree_Path t ON f.id = t.ancestor
WHERE t.descendant=:id

И также подобно, как и в случае с получением потомков (см. детальное пояснение в разделе 2.4) в результате запроса будет не только список всех родителей, но и узел для которого собственно и производится выборка родителей. Дабы исключить ссылку на самого себя, необходимо в запрос добавить ещё одно условие descendant!=ancestor. Думаю, что этот момент ясен. Ниже приведён пример именованного запрос для получения всех родителей с уровнем вложенности:

<named-native-query name="getAllParents" 
                    result-set-mapping="FileNameWithLevelMapping">
    <query> 
        <![CDATA[        
        WITH parents AS
        (SELECT p.id, p.name, count(*) - l.level AS level
        FROM tree_Path t,
        -- (1) get the levels of all nodes.
        (SELECT descendant, count(*) AS level
        FROM tree_path
        GROUP BY descendant) l,
        -- (2) get all parents.
        (SELECT *
        FROM file_name f
        INNER JOIN tree_Path t ON f.id = t.ancestor
        WHERE t.descendant=:id AND t.descendant != t.ancestor) p

        WHERE p.descendant = t.descendant AND t.descendant!=t.ancestor AND l.descendant=p.id
        GROUP BY p.id, p.name, l.level)
        -- Result Query
        SELECT id, name, (SELECT max(level) FROM parents) - level + 1 AS level
        FROM parents
        ]]>
    </query>
    <hint name="org.hibernate.comment" value="Get Parents By ID"/>
</named-native-query>

Перейдём к телу запроса и кратко опишем.

В данном запросе используется обобщённое табличное выражение с целью улучшить немного читаемость кода путём разделения на логический блок с псевдонимом parents. Разобьём запрос условно на части и опишем каждый его подзапрос помеченный комментарием с номером.

(1) Подзапрос необходим для получения значений уровней вложенности для всех узлов дерева.

(2) Подзапрос служит для получения всех родителей узла с идентификатором :id. Этот запрос уже был представлен ранее в самом начале раздела 2.5.

В обобщённом табличном выражении все подзапросы и таблица tree_path соединяются и производится подсчёт уровня вложенности всех родителей для узла с идентификатором :id. Так как уровень вложенности идёт в обратном порядке, то уже в последнем результирующем запросе с целью исправить порядок, добавлен такой запрос: (SELECT max(level) FROM parents) - level + 1. В итоге получим список всех родителей с уровнем вложенности, где порядок идёт от корневого узла.

2.6. Добавление узла в дерево

public void add(FileName parentNode, FileName node) {
    save(node); //(1)
    Session session = HibernateUtil.getSessionFactory().getCurrentSession();
    session.beginTransaction();
    //(2)
    session.createNamedQuery("addChildren")
            .setParameter("parentId", parentNode.getId())
            .setParameter("childId", node.getId())
            .executeUpdate();
    session.getTransaction().commit();
}

Добавление узла в дерево происходит в 2 этапа:

(1) Сохраняем узел со всеми связями (вся иерархия поддерева) в таблицы: FILE_NAME, TREE_PATH.

(2) Связываем добавленный узел со всеми родительскими узлами. Именованный запрос приведён ниже.

<named-native-query name="addChildren">
    <query>
       <![CDATA[
        INSERT INTO tree_path(ancestor, descendant) 
        SELECT a.ancestor, d.descendant
        FROM
        -- (1) get all parents by ID.
        (SELECT ancestor
        FROM tree_Path
        WHERE descendant = :parentId) a,
        -- (2) get all descendants by ID.
        (SELECT descendant 
        FROM tree_path 
        WHERE ancestor = :childId) d
        ]]>
    </query>
    <hint name="org.hibernate.comment" value="Add Subtree By ID"/>
</named-native-query>

Перейдём к телу запроса и кратко опишем.

Приведённый запрос добавляет новый узел или целое поддерево к конкретному родительскому узлу с идентификатором :parentId путём вставки в таблицу TREE_PATH новых связей.

(1) Подзапрос служит для получения всех родителей того узла дерева к которому будет добавлен новый узел или поддерево.

(2) Подзапрос необходим для получения всех потомков поддерева.

Далее производим перекрёстное соединение, или декартово произведение CROSS JOIN двух подзапросов (1), (2) и этот результат вносим в таблицу TREE_PATH. Запрос добавит в каждый родительский узел вверх по иерархии новый узел в качестве потомка.

2.7. Удаление узла из дерева

Для удаления узла со всеми его потомками потребуется произвести SQL операцию Delete в двух таблицах: в основной FILE_NAME и в таблице связей TREE_PATH. Для этих целей можно воспользоваться такими способами:

Произвести удаление поочерёдно для каждой таблицы. Первым запросом производим удаление узла со всеми его потомками из таблицы связей TREE_PATH, дабы не нарушить ограничение внешнего ключа. А вторым запросом удаляем все записи из таблицы FILE_NAME, идентификаторы которых отсутствуют в таблице связей TREE_PATH.
Произвести удаление с помощью Multiple Table Delete Syntax - удаление записей одним запросом из 2-х и более таблиц. Но такой способ удаления записей поддерживается не каждой БД.
Воспользоваться наличием у таблицы TREE_PATH внешних ключей и задать в схеме для них каскадное удаление (ON DELETE CASCADE). В этом случае для удаления записей понадобиться всего один запрос для основной таблицы FILE_NAME, а все связанные строки из зависимой таблицы связей TREE_PATH будут удалены автоматически на уровне БД.

Привожу в качестве примера 3-й способ. Ниже приведён именованный запросов для удаления узла со всеми его потомками.

<named-native-query name="delete">
    <query>
       <![CDATA[
        DELETE 
        FROM file_name
        WHERE id IN
        (SELECT descendant
        FROM tree_Path 
        WHERE ancestor=:id)
        ]]>
    </query>
    <hint name="org.hibernate.comment" value="Delete Node By ID"/>
</named-native-query>

Как видим из запроса, удаление записей производится только в таблице FILE_NAME. Для того чтобы использовать этот запрос, необходимо удостовериться, что в схеме таблицы связей TREE_PATH задано каскадное удаление, иначе при выполнении запроса получим ошибку нарушения ограничения внешнего ключа.

Ниже приведён пример, который указывает, что в схеме таблицы (TREE_PATH) задано каскадное удаление для внешних ключей ancestor и descendant.

CONSTRAINT fk_ancestor FOREIGN KEY (ancestor)
    REFERENCES file_name (id) MATCH SIMPLE
    ON DELETE CASCADE,
CONSTRAINT fk_descendant FOREIGN KEY (descendant)
    REFERENCES file_name (id) MATCH SIMPLE
    ON DELETE CASCADE

2.8. Перемещение узла в дереве

Перемещение узла со всеми его потомками (поддерево) для Closure Table - это довольно не простая операция. Эту операцию, я разбил на 2 этапа:

Удаление всех родителей, которые после перемещения узла уже не будут являться для него таковыми.
Определение новых родителей для перемещаемого узла и добавление их в таблицу связей TREE_PATH.

1-й этап - удаление родительских связей из таблицы TREE_PATH.

<named-native-query name="move-deleteParents">
    <query>
       <![CDATA[
        DELETE
        FROM tree_Path t
        WHERE t.descendant IN
        -- (1) get all descendants by id.
            (SELECT descendant
             FROM tree_Path
             WHERE ancestor = :childId)

          AND t.ancestor IN

          -- (2) get all different ancestors.
            (SELECT a.ancestor
             FROM
               (SELECT ancestor
                FROM tree_Path
                WHERE descendant = :childId
                  AND descendant != ancestor) a
             LEFT JOIN
               (SELECT ancestor
                FROM tree_path
                WHERE descendant = :parentId
                  AND descendant != ancestor) d ON a.ancestor = d.ancestor
             WHERE d.ancestor IS NULL)
        ]]>
    </query>
    <hint name="org.hibernate.comment" value="Move Subtree By ID (delete parents)"/>
</named-native-query>

Перейдём к телу запроса и кратко опишем.

(1) Подзапрос необходим для получения всех потомков (всё поддерево) перемещаемого узла.

(2) Подзапрос необходим для получения всей цепочки родителей, которая отличается от цепочки предков нового родительского узла. Новый родительский узел - это то место в дереве, куда будет перемещён наш узел.

В результате операции Delete будут удалены все родительские узлы для перемещаемого поддерева, которые после перемещения уже не будут являться для него предками.

2-й этап - определение списка новых родителей в иерархии и добавление новых связей в таблицу TREE_PATH.

<named-native-query name="move-addChildren">
        <query>
           <![CDATA[
            INSERT INTO tree_path(ancestor, descendant)
            SELECT parent.ancestor, child.descendant
              FROM
              -- (1) get all new parents in the hierarchy.
              (SELECT a.ancestor
                    FROM
                    (SELECT ancestor
                    FROM tree_Path
                    WHERE descendant = :parentId) a            
              LEFT JOIN            
                    (SELECT ancestor 
                    FROM tree_path 
                    WHERE descendant = :childId) d            
              ON a.ancestor = d.ancestor
              WHERE d.ancestor IS NULL) parent,

              -- (2) get all descendants by id.
              (SELECT descendant 
               FROM tree_path 
               WHERE ancestor = :childId) child
            ]]>
        </query>
        <hint name="org.hibernate.comment" value="Move Subtree By ID (add children)"/>
</named-native-query>

Перейдём к телу запроса и кратко опишем.

(1) Подзапрос необходим для получения списка новых родителей в иерархии, которые нужно добавить в таблицу связей TREE_PATH.

(2) Подзапрос необходим для получения всех потомков (всё поддерево) перемещаемого узла.

Далее производим перекрёстное соединение, или декартово произведение CROSS JOIN двух подзапросов (1), (2) и этот результат вносим в таблицу TREE_PATH. Запрос добавит новых родителей для узла или целого поддерева.

Ниже приведён пример метода на языке java позволяющий переместить узел в дереве. В методе используются именованные SQL запросы, которые были приведены и кратко описаны выше.

public void move(FileName parentNode, FileName subNode) {
    Session session = HibernateUtil.getSessionFactory().getCurrentSession();
    session.beginTransaction();
            session.createNamedQuery("move-deleteParents")
            .setParameter("parentId", parentNode.getId())
            .setParameter("childId", subNode.getId())
            .executeUpdate();
    session.createNamedQuery("move-addChildren")
            .setParameter("parentId", parentNode.getId())
            .setParameter("childId", subNode.getId())
            .executeUpdate();
    session.getTransaction().commit();
}

2.9. Преимущества и недостатки

Преимущества:

ссылочная целостность данных;
простая операция удаление узла со всеми его потомками благодаря ссылочной целостности (ON DELETE CASCADE);
простая операция получения потомков без уровня вложенности;
простая операция получения родителей без уровня вложенности;
простая операция добавления узла в дерево.

Недостатки:

большое количество записей в таблице связей из-за необходимости хранить связи каждого элемента дерева со всеми его предками;
перемещение узла со всеми его потомками.

Стоит также отметить, что размер таблицы связей может меняться не только от операций добавления или удаления узла, но и от операции перемещения. В случае операции перемещения возможны оба варианта, как увеличение количества записей в таблице связей, так и уменьшение, всё зависит от того на какую глубину вложенности будет перемещён узел.

Подсчёт уровня вложенности является не простой операцией, которая оказывает влияние на скорость выполнения запроса. Будет уместным перенести уровень вложенности в основную таблицу FILE_NAME и пересчитывать его уже при модификации дерева, если важно, чтобы операции получения потомков и родителей выполнялись максимально быстро из возможного.

Далее пойдут способы представления дерева, где один из основных недостатков является отсутствие ссылочной целостности. Поддержка целостности данных ложиться полностью на плечи разработчика в буквальном смысле. А также вся логика базовых операций с деревом на уровне DAO будет описана полностью с помощью SQL запросов.

3. Вложенные множества (Nested sets)

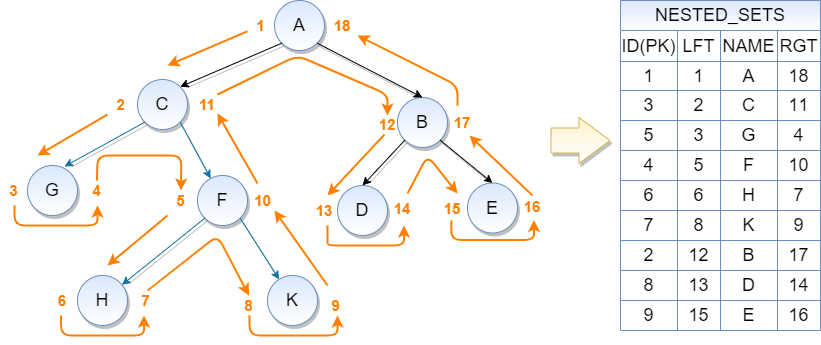
На рисунке показано дерево, которое описано по правилам модели "Вложенные множества". По нему видно, что каждый узел дерева имеет 2 значения: Left (значение слева от узла) и Right (значение справа от узла). Процедура определения этих значений совсем несложная и состоит в обходе дерева слева на право и наращивании счётчика на 1 при прохождении узла. На рисунке оранжевыми стрелками показан процесс обхода дерева. Результат обхода отображён в таблице NESTED_SETS слева на рисунке. Слова Left и Right являются зарезервированными и поэтому в таблице NESTED_SETS они заменены на LFT и RGT.

Пример:

Получим потомков для узла C у которого Left = 2 и Right = 11. Для этого понадобиться такой запрос:

SELECT * FROM NESTED_SETS WHERE LFT > 2 AND RGT < 11

В результате получим полный список дочерних узлов G, F, H, K. А также по значениям Left и Right можно определить наличие или отсутствие у узла дочерних элементов без отправки запроса в БД, если разница (Right - Left) равна 1, то у узла нет дочерних элементов, а значение большее >1 указывает на наличие таких элементов. Количество дочерних узлов можно определить по такой формуле: (Right - Left - 1)/2.

Для получения полного списка родителей для узла C необходимо выполнить следующий запрос:

SELECT * FROM NESTED_SETS WHERE LFT < 2 AND RGT > 1

Результат будет содержать только одного родителя A, что соответствует рисунку выше. В случае, когда список родителей больше одного элемента, значение Left и Right можно использовать для упорядочивания этого списка, то есть задать уровень вложенности. К примеру, если необходимо задать порядок родителей начиная с корневого узла и дальше по уровню вложенности, то в SQL запрос достаточно добавить ORDER BY LFT ASC или ORDER BY RGT DESC.

3.1. Сущность NestedSetsTree

@Entity
@Table(name = "nested_sets", indexes = {
    @Index(name = "IDX_LFT", columnList = "lft"),
    @Index(name = "IDX_RGT", columnList = "rgt")})
@DynamicUpdate
public class NestedSetsTree implements Serializable {

    @Id
    @GeneratedValue(strategy = GenerationType.IDENTITY)
    private long id;
    @NotNull
    private String name;
    @NotNull
    @Column(name = "lft")
    private long left;
    @NotNull
    @Column(name = "rgt")
    private long right;

//default constructor   
// getters
// setters
...
}

Сущность NestedSetsTree - это простая модель таблицы NESTED_SETS, которая приведена на рисунке выше. Сущность содержит аннотации @Index для колонок LFT и RGT с целью ускорения получения данных. А также добавлена аннотация @DynamicUpdate для активации динамического создания UPDATE запросов, то есть запрос на обновление будет содержать столбцы только с новыми значениями, а не все, как по умолчанию. По сути на этом можно и закончить краткое описание.

3.2. Получение всех потомков

<named-native-query name="getAllСhildren" result-set-mapping="NestedSetsTreeWithLevelMapping">
 <query>
<![CDATA[         
WITH node AS
  (SELECT descendant.id, descendant.name, descendant.lft, descendant.rgt, COUNT(*) AS LEVEL
   FROM
		-- (1) get all descendants by id.
     (SELECT ch.*
      FROM nested_sets n,
           nested_sets ch
      WHERE n.id = :id AND ch.lft > n.lft AND ch.rgt < n.rgt) descendant,
      nested_sets parent
   WHERE descendant.lft BETWEEN parent.lft AND parent.rgt
   GROUP BY descendant.id, descendant.name, descendant.lft, descendant.rgt)
-- Result Query
SELECT id, name, lft, rgt, (LEVEL - (SELECT min(LEVEL) FROM node) +1) AS LEVEL
FROM node
]]>
</query>
<hint name="org.hibernate.comment" value="Get Сhildren By ID"/>
</named-native-query>

Перейдём к телу запроса и кратко опишем.

В данном запросе используется обобщённое табличное выражение с целью немного упростить код. Под комментарием (1) размещён подзапрос для получения всех потомков для узла с идентификатором :id. Далее производим группировку и подсчитываем уровень вложенности для всех потомков. В последнем результирующем запросе пересчитываем уровень вложенности, чтоб отсчёт шёл от родительского узла, а не от корневого. В итоге получим список всех потомков с уровнем вложенности.

3.3. Получение всех родителей

<named-native-query name="getAllParents" result-set-mapping="NestedSetsTreeWithLevelMapping">
     <query> 
         <![CDATA[        
            SELECT p.id, p.name, p.lft, p.rgt, ROW_NUMBER() over(ORDER BY p.lft ASC) AS LEVEL 
            FROM nested_sets n, nested_sets p
            WHERE n.id = :id AND p.lft < n.lft AND p.rgt > n.rgt
          ]]>
     </query>
     <hint name="org.hibernate.comment" value="Get Parents By ID"/>
</named-native-query>

Перейдём к телу запроса и кратко опишем.

Данный запрос достаточно простой и в детальных комментариях и описаниях по сути не нуждается. Здесь можно обратить внимание на вычисление уровня вложенности, которое производится простой функцией нумерации ROW_NUMBER. Ранее в самом начале главы упоминалось, чтоб задать порядок родителей от корневого узла, достаточно будет произвести сортировку ORDER BY LFT ASC или ORDER BY RGT DESC. Поэтому с помощью функции ROW_NUMBER() over(ORDER BY p.lft ASC) по столбцу LFT будут сначала отсортированы данные, а потом пронумерованы. Таким образом в итоге получим список всех родителей с уровнем вложенности, где порядок идёт от корневого узла.

3.4. Добавление узла в дерево

Ниже представлен рисунок, который демонстрирует процесс добавления поддерева в дерево. На рисунке к узлу H добавляем узел L с потомком M. Стоит обратить внимание на то, как изменятся значения LEFT и RIGHT для узлов дерева после добавления поддерева.

Процесс добавления узла с потомками можно разбить на три этапа.

Перед тем, как добавить узел в качестве прямого потомка другого узла, необходимо выделить пространство в дереве. Поэтому первые 2 этапа - это выделение пространства для нового узла. Обзовём размер выделяемого пространства значением delta и приведём формулу: delta = SIZE * 2, где SIZE - это количество добавляемых узлов в дерево. В нашем случае в дерево будет добавлено 2 узла L и M, поэтому delta = 2*2 =4.

1) Увеличиваем все LEFT значения на delta, если они больше или равны значению RIGHT непосредственного родителя. В нашем случае непосредственным родителем для добавляемого узла является узел H со значением RIGHT = 7, а delta была рассчитана ранее и равна 4.

UPDATE nested_sets SET LFT = LFT + 4 WHERE LFT >= 7

2) Увеличиваем все RIGHT значения на delta, если они больше или равны значению RIGHT непосредственного родителя. Для узла H RIGHT = 7, а delta = 4.

UPDATE nested_sets SET RGT = RGT + 4 WHERE RGT >= 7

3) Добавляем узел в уже выделенное пространство. Производим инициализацию всех значений LEFT и RIGHT для добавляемого узла, где начальным значением отсчёта будет являться число LEFT + 1 непосредственного родителя. В нашем случае непосредственный родитель является узел H со значением LEFT = 6. Следовательно, для узла L значения LEFT = 7, RIGHT = 10, а для его потомка M значения LEFT = 8, RIGHT = 9, всё согласно правилам данной модели представления. После инициализации производим добавление узла (INSERT) в БД. В результате узел L с потомком M займёт уже выделенное пространство в дереве, как показано на рисунке внизу.

3.5. Удаление узла из дерева

Ниже представлен рисунок, который демонстрирует процесс удаление узла с потомками из дерева. Здесь стоит обратить внимание на то, как меняются значения LEFT и RIGHT после удаления узла F со всеми его потомками.

Процесс удаления узла с потомками можно разбить на три этапа.

Процесс удаления узла с потомками подразумевает, как удаление поддерева, так и занимаемое им пространство. Поэтому 2 последних этапа - это удаление занимаемого пространства, путём уменьшения значений LEFT и RIGHT на delta. Приведём формулу: delta = RIGHT - LEFT + 1, где LEFT и RIGHT являются значениями удаляемого узла. Подсчитаем delta для удаляемого узла F: delta = 10 - 5 +1= 6.

1) Удаление узла. Ниже представлен именованный запрос для удаления узла целиком со всеми потомками.

    <named-native-query name="delete">
        <query>
           <![CDATA[
            DELETE FROM nested_sets WHERE id IN (
            SELECT descendant.id FROM nested_sets parent
            INNER JOIN nested_sets descendant
            ON (descendant.lft BETWEEN parent.lft and parent.rgt)
            WHERE parent.id = :id)
            ]]>
        </query>
        <hint name="org.hibernate.comment" value="Delete Node By ID"/>
    </named-native-query>

2) Уменьшаем все LEFT значения на delta, если они больше значения LEFT удаляемого узла. Подсчитаем для удаляемого узла F: delta = RIGHT - LEFT + 1 = 10 - 5 +1= 6, а значение LEFT=5.

UPDATE nested_sets SET LFT = LFT - 6 WHERE LFT > 5

3) Уменьшаем все RIGHT значения на delta, если они больше значения RIGHT удаляемого узла. Значение delta для узла F уже было подсчитано ранее delta = 6, значение RIGHT=10.

UPDATE nested_sets SET RGT = RGT - 6 WHERE RGT > 10

В результате узел F будет удалён, а значения LEFT и RIGHT будут пересчитаны согласно правилам модели "Вложенные множества".

3.6. Перемещение узла в дереве

Ниже представлен рисунок, который демонстрирует процесс перемещения узла с потомками внутри дерева. Здесь также стоит обратить внимание на то, как меняются значения LEFT и RIGHT после перемещения поддерева.

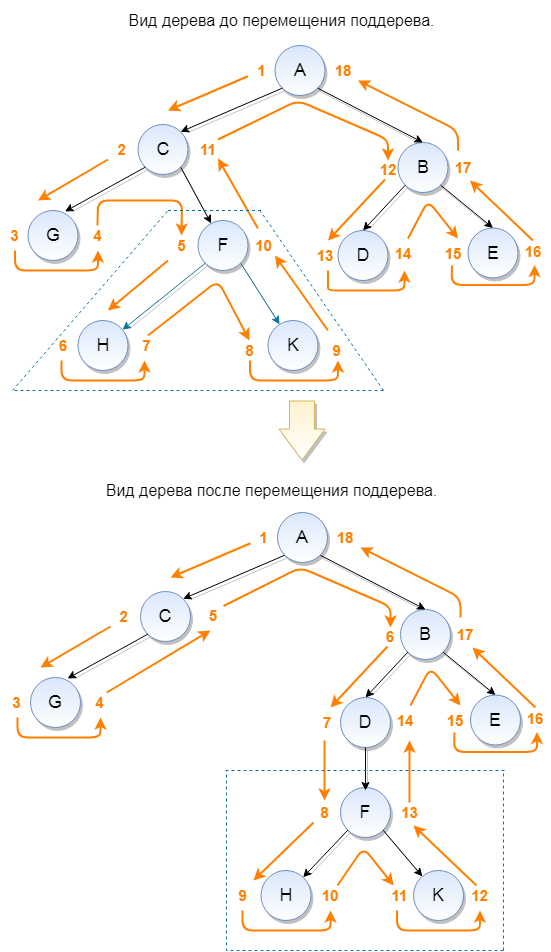
Операция перемещения узла или поддерева является одной из самых непростых в данной модели представления дерева. Операцию перемещения можно представить, как две операции: удаление и затем добавление узла со всеми его потомками, которые были уже описаны ранее (см. 3.5, 3.6). И да, конечно, можно так и поступить, просто заменив перемещение на 2 операции: удаление и добавление, но они будут изначально содержать избыточные действия, такие как удаление (DELETE) всех записей из таблицы NESTED_SETS относящихся к перемещаемому узлу и затем добавление (INSERT) в эту же таблицу ранее удалённых записей, что естественно окажет негативное влияние на производительность. Поэтому эту идею необходимо доработать, а именно для целей перемещения узла/поддерева убрать избыточные операции непосредственного удаления (DELETE) и добавления (INSERT) записей в таблицу NESTED_SET, оставив только процедуры выделения и удаления пространства, что производится путём пересчёта значений LEFT и RIGHT для всех затрагиваемых узлов дерева.

Процесс перемещения узла с потомками можно разбить на три этапа.

1) Выделение пространства для нового узла с потомками. Назовём условно размер необходимого пространства значением delta и подсчитаем его. Формула размера пространства следующая: delta = RIGHT - LEFT + 1. Для перемещаемого узла F: delta = 10 - 5 + 1 = 6.

1.1) Увеличиваем все LEFT значения на delta, если они больше или равны значению RIGHT нового родителя. В нашем случае родителем для перемещаемого узла F станет узел D со значением RIGHT = 14, а delta была рассчитана ранее и равна 6.

UPDATE nested_sets SET LFT = LFT + 6 WHERE LFT >= 14

1.2) Увеличиваем все RIGHT значения на delta, если они больше или равны значению RIGHT нового родителя. Для узла D RIGHT = 14, а delta = 6.

UPDATE nested_sets SET RGT = RGT + 6 WHERE RGT >= 14

2) Вставка узла с потомками в уже выделенное пространство путём пересчёта значений LEFT и RIGHT для всех его узлов. Значение на которое необходимо пересчитать узлы, также условно назовём delta и приведём формулу: delta = parentLEFT - subNodeLEFT + 1, где parentLEFT - это значение LEFT для нового родителя (узел, который станет родительским после перемещения поддерева), subNodeLEFT - это значение LEFT для перемещаемого узла. В нашем случае для узла D значение parentLEFT = 13, а для узла F значение subNodeLEFT = 5 (см. рисунок выше "Вид дерева до перемещения поддерева"). В итоге delta = 13 - 8 +1 = 6. Ниже представлен запрос, который обновляет (пересчитывает) значения LEFT и RIGHT для узла F со всеми его потомками.

UPDATE nested_sets SET lft = lft + 6, rgt = rgt + 6 WHERE id in
(SELECT descendant.id FROM nested_sets parent
INNER JOIN nested_sets descendant
ON (descendant.lft BETWEEN parent.lft and parent.rgt)
WHERE parent.id = 4)

Запрос UPDATE содержит подзапрос, который возвращает все идентификаторы узлов поддерева. В подзапросе значение parent.id = 4 - это идентификатор узла F из таблицы NESTED_SETS (смотри рисунок выше "Вложенные множества").

Важно! Значение delta необходимое для пересчёта узлов может быть, как положительным, так и отрицательным значением и зависит от того в какую часть дерева будет перемещён узел с потомками.

3) Удаление ранее занятого пространства в дереве. Назовём также условно размер удаляемого пространства значением delta и приведём формулу: delta = RIGHT - LEFT + 1. Как видим всё аналогично, как и для выделения пространства, разница лишь в том, что в этом случае уменьшаем значения LEFT и RIGHT для всех затрагиваемых узлов. Подсчитаем для узла F: delta = 10 - 5 + 1 = 6.

3.1) Уменьшаем все LEFT значения на delta, если они больше значения RIGHT перемещаемого узла. Для перемещаемого узла F: delta = 6, а значение RIGHT = 10.

UPDATE nested_sets SET LFT = LFT - 6 WHERE LFT > 10

3.2) Уменьшаем все RIGHT значения на delta, если они больше значения RIGHT перемещаемого узла. Для перемещаемого узла F: delta = 6, а значение RIGHT = 10.

UPDATE nested_sets SET RGT = RGT - 6 WHERE RGT > 10

В результате получим дерево с перемещённым поддеревом, которое представлено на рисунке выше с названием "Вид дерева после перемещения поддерева". Перемещённое поддерево помечено синим прямоугольником.

3.7. Преимущества и недостатки

Преимущества:

простая операция получения потомков без уровня вложенности;
простая операция получения родителей;

Недостатки:

отсутствует ссылочная целостность;
удаление узла;
добавление узла;
перемещение узла;
операция подсчёта уровня вложенности для потомков узла.

Главной причиной недостатков операций удаления, добавления и перемещения узла является необходимость пересчёта значений LEFT и RIGHT для всех затронутых узлов в дереве, что существенно отражается на производительности.

Не простая операция подсчёта уровня вложенности для всех потомков узла, также оказывает серьёзное влияние на производительность особенно, если дерево достаточно большое. Как правило "Вложенные множества" выбирают для быстрых операций выборки всех потомков и предков, поэтому для данного способа скорее всего будет уместным перенести уровень вложенности в таблицу и пересчитывать его при каких либо изменениях в дереве.

4. Материализованный путь (Materialized Path)

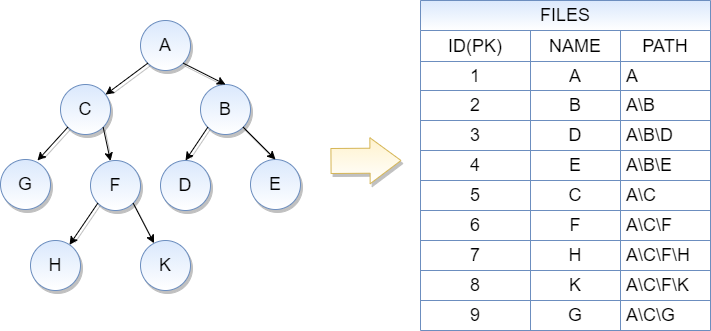
На рисунке продемонстрирован пример модели "Материализованный путь". Идея данной модели заключается в хранении полного пути для каждого узла в дереве. В пути (path) храниться цепочка всех предков для каждого узла. По количеству разделителей в пути можно определить глубину вложенности узла. Модель "Материализованные путь" является наглядным и наиболее интуитивно понятным представлением дерева.

4.1. Сущность (Entity) для Materialized Path

@Entity
@Table(name = "files", indexes = @Index(name = "IDX_PATH", columnList = "path"))
@DynamicUpdate
public class Files implements Serializable {
    @Id
    @GeneratedValue(strategy = GenerationType.IDENTITY)
    private long id;
    @NotNull
    @Column(length = 1000)
    private String path;
    @NotNull
    private String name;
  
//default constructor 
// getters
// setters
  ...
}

Сущность Files - это простая модель таблицы FILES, которая приведена на рисунке выше. Сущность содержит аннотации @Index для колонки PATH с целью ускорения получения данных. А также добавлена аннотация @DynamicUpdate для активации динамического создания UPDATE запросов, то есть запрос на обновление будет содержать столбцы только с новыми значениями, а не все, как по умолчанию. По сути на этом всё.

4.2. Получение всех потомков

    <named-native-query name="getAllСhildren" 
                        result-set-mapping="FilesWithLevelMapping">
        <query> 
            <![CDATA[        
            SELECT *,
 			-- (1) get level of a node. 
		   ( length(path) - length(replace(path, :delimiter, ''))
            - (length(:parentPath) - length(replace(:parentPath, :delimiter, '')) + 1) + 1) as level 
            ----------------------------------------------------------------------------------------
            FROM files 
            WHERE path like :parentPath || :delimiter ||'%'
            ]]>
        </query>
        <hint name="org.hibernate.comment" value="Get Сhildren By Parent Path"/>
    </named-native-query>

Перейдём к телу запроса и кратко опишем.

Выше приведён именованный запрос для получения всех потомков на основании пути родительского узла. Сам запрос поиска потомков достаточно прост, а вот вычисления уровня вложенности путём подсчёта разделителей в SQL уже достаточно громоздкая операция, поэтому для упрощения запроса её можно просто перенести, либо в хранимую процедуру БД, либо в java код. К сожалению, не каждая БД имеет подходящую функцию для подсчёта количества разделителей в строке.

4.3. Получение всех родителей

    <named-native-query name="getAllParents" 
                        result-set-mapping="FilesWithLevelMapping">
        <query> 
            <![CDATA[
            -- Recursive Query
            WITH RECURSIVE cte (PATH, LEVEL) AS
            (SELECT split_part(PATH, :delimiter, 1), 1 AS LEVEL
             FROM files
             WHERE id = :id
             UNION ALL 
             SELECT CONCAT (c.path, :delimiter, split_part(f.path, :delimiter, LEVEL+1)), LEVEL + 1
             FROM cte c,
                  files f
             WHERE f.id = :id AND f.path!=c.path)
          -- Result Query  
          SELECT f.*, c.level
          FROM cte c,
               files f
          WHERE 
                f.path=c.path
            ]]>
        </query>
        <hint name="org.hibernate.comment" value="Get Parents By Paths"/>
    </named-native-query>

Перейдём к телу запроса и кратко опишем.

Выше приведён именованный запрос для получения всех родителей на основе пути узла. Запрос состоит из рекурсивного и результирующего запроса. Рекурсивный запрос требуется только для того, чтобы получить уровень вложенности и список путей для всех родителей через разбиения строки PATH. Результирующий запрос осуществляет поиск всех родителей по пути.

4.4. Добавление узла в дерево

Ниже приведён пример метода на языке java позволяющий добавить узел в дерево.

    public void add(Files parentNode, Files childNode) {
        String newPath = String.join(File.separator, parentNode.getPath(), childNode.getName());
        childNode.setPath(newPath);
        Session session = HibernateUtil.getSessionFactory().getCurrentSession();
        session.beginTransaction();
        session.save(childNode);
        session.getTransaction().commit();
    }

Операция добавления узла достаточно простая, требуется всего лишь составить путь потомка, что производится путём конкатенации пути непосредственного родителя и имени узла потомка.

4.5. Удаление узла из дерева

    <named-native-query name="delete">
        <query>
           <![CDATA[
            DELETE
            FROM Files
            WHERE path LIKE :path || :delimiter ||'%' OR path = :path
            ]]>
        </query>
        <hint name="org.hibernate.comment" value="Delete Node By Path"/>
    </named-native-query>

Выше представлен именованный запрос для удаления узла со всеми его потомками.

4.6. Перемещение узла в дереве

<named-native-query name="move">
     <query>
     <![CDATA[
		UPDATE files
		SET PATH = REPLACE(PATH, :subNodeParentPath, :parentPath)
		WHERE  path LIKE :subNodeParentPath || :delimiter ||'%' OR path = :subNodeParentPath
     ]]>
     </query>
    <hint name="org.hibernate.comment" value="Move Node By Path"/>
</named-native-query>

Выше представлен именованный запрос для перемещения узла со всеми его потомками. Перемещение узла осуществляется через операцию замена (REPLACE) цепочки родителей в строке path. В именованном запросе содержатся такие параметры: subNodeParentPath и parentPath, где subNodeParentPath - путь непосредственного родителя перемещаемого узла, parentPath - путь нового родительского узла, то есть это место в дереве, куда будет перемещён узел. Ниже приведён пример метода на языке java использующий именованные запрос выше и позволяющий переместить узел в дереве.

    public void move(Files parentNode, Files subNode) {
        String subNodeParentPath = StringUtils.removeEnd(subNode.getPath(), File.separator + subNode.getName());
        Session session = HibernateUtil.getSessionFactory().getCurrentSession();
        session.beginTransaction();
        session.createNamedQuery("move")
                .setParameter("subNodeParentPath", subNodeParentPath)
                .setParameter("parentPath", parentNode.getPath())
                .setParameter("delimiter", File.separator)
                .executeUpdate();
        session.getTransaction().commit();
    }

4.7. Преимущества и недостатки

Рассмотрим преимущества с точки зрения простоты запроса.

Преимущества:

простой запрос получения потомков;
простой запрос получения родителей;
простой запрос удаления узла;
простой запрос перемещения узла;

Недостатки:

отсутствует ссылочная целостность;
операция подсчёта уровня вложенности узла (не во всех БД имеются необходимые функции для эффективной работы со строками).

Основной недостаток - это неэффективность запросов из-за поиска по подстроке.

Из всех рассмотренных способов хранения древовидной структуры в реляционной базе данных, каждый способ имеет свои, как достоинства, так и недостатки. Только исходя из требований конкретной задачи можно принять решение в пользу какого-то из способов.

Примеры моей реализаций всех описанных в этом посте способов представлений дерева можно посмотреть на GitHub (Adjacency List, Closure Table, Nested sets, Materialized Path).

Комментарии (3)

furic
07.06.2021 19:02
#23124674
Если отказаться от Lazy load (первый вариант) , все дерево подгрузится само, нет?
1. Ivan_Yuriev Автор
  07.06.2021 20:57
  #23124948
  Я так понимаю отказаться от Lazy имеется ввиду заменить на EAGER. Да, загрузится дерево, но для этого ORM Hibernate сгенерирует множество SQL запросов, чтоб загрузит все связанные узлы потомки, что будет неэффективно, как по количеству отправленных запросов в БД, так и затраченному на всё это времени. И к тому же, если установлен EAGER, Hibernate будет всегда загружать все связанные узлы, а это ещё и большие затраты по памяти.
1. kacetal
  08.06.2021 14:42
  #23127338
  Для этого лучше Entity Graph использовать , а не Eager

Способы хранения деревьев в реляционных базах данных c использованием ORM Hibernate +9

1. Список смежности (Adjacency List)

1.1. Сущность (Entity) для Adjacency List

Краткое описание сущности (только важное)

1.2. Получение всех потомков

1.3. Получение всех родителей

1.4. Добавление узла в дерево

1.5. Удаление узла из дерева

1.6. Перемещение узла в дереве

1.7. Преимущества и недостатки

2. Таблица связей (Closure Table)

2.1. Сущность FileName

Краткое описание сущности (только важное)

2.2. Сущность TreePath

Краткое описание сущности (только важное)

2.3. IdClass TreePathId

2.4. Получение всех потомков

2.5. Получение всех родителей

2.6. Добавление узла в дерево

2.7. Удаление узла из дерева

2.8. Перемещение узла в дереве

2.9. Преимущества и недостатки

3. Вложенные множества (Nested sets)

3.1. Сущность NestedSetsTree

3.2. Получение всех потомков

3.3. Получение всех родителей

3.4. Добавление узла в дерево

3.5. Удаление узла из дерева

3.6. Перемещение узла в дереве

3.7. Преимущества и недостатки

4. Материализованный путь (Materialized Path)

4.1. Сущность (Entity) для Materialized Path

4.2. Получение всех потомков

4.3. Получение всех родителей

4.4. Добавление узла в дерево

4.5. Удаление узла из дерева

4.6. Перемещение узла в дереве

4.7. Преимущества и недостатки

Комментарии (3)

furic

Ivan_Yuriev Автор

kacetal