15.06.2021 09:00
urmaas 8 5400 Источник

Впервые увидел этот странный график в лаборатории университета. Невзрачный листок, ксерокопированный из старой книги, был наклеен на стену рядом с роторным испарителем. Листок, очевидно, использовали часто, но берегли, словно в нём содержалось какое-то древнее могучее заклинание… Впоследствии, схожего рода графики попадались мне и в других лабораториях, словно составляли неотъемлемую часть перегонки с вакуумом. Затем похожие рисунки встречались на страницах разной технической литературы. Их называли номограммы. Научиться ими пользоваться оказалось до смешного просто, но кто и как их в своё время сделал — оставалось загадкой.


Как выглядят номограммы и как они работают


Номограмма, что часто используется при перегонке с вакуумом приведена на рисунке ниже.


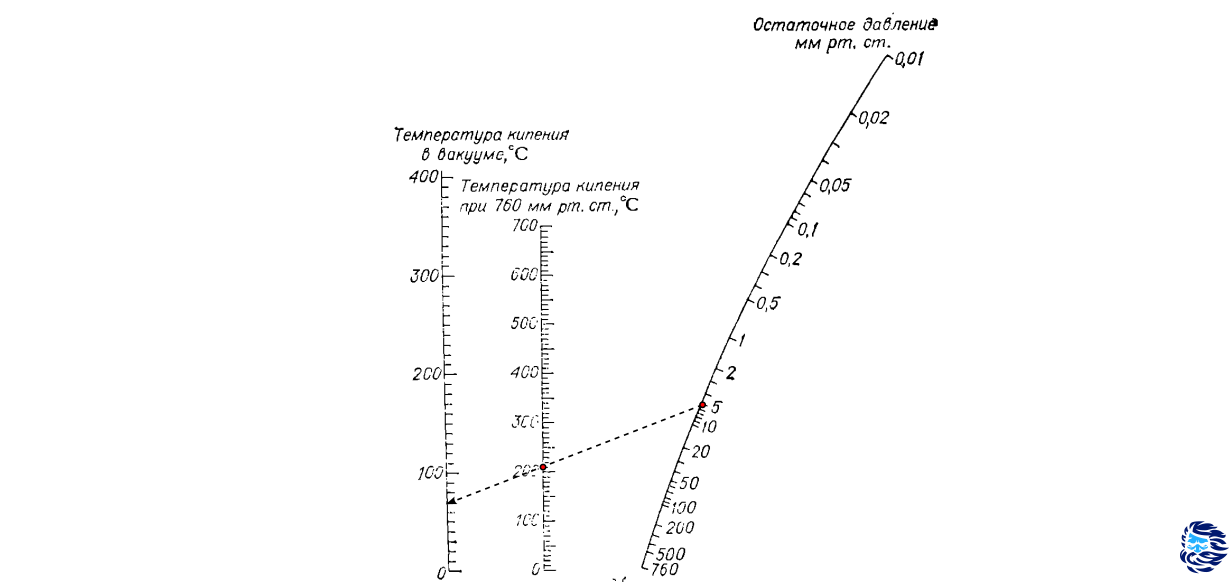
Допустим, вы провели реакцию в растворителе, а теперь собираетесь его удалить (выпарить), чтобы собрать продукт реакции. Растворитель улетучивается изнурительно медленно, а чтобы ускорить процесс, вы решаете его нагреть, но вот беда — греть раствор нежелательно, так как продукт реакции от нагревания может испортиться. Создав пониженное давление, вы уменьшите температуру кипения растворителя и сумеете его отделить не причинив вреда растворенному в нем веществу. При нормальном атмосферном давлении 760 мм ртутного столба вода кипит при 100 С, однако, при давлении 40 мм кипит уже при 34 С.


А как быть с гамма-бутиролактоном, который кипит при 204 С? Отмечаем на оси "Температура кипения при 760 мм" точку 204 С, выставляем на кривой оси "Остаточное давление" 5 мм, проводим прямую до пересечения с третьей осью. Ага, значит, в этих условиях наш растворитель начнет выкипать примерно при 70 С.


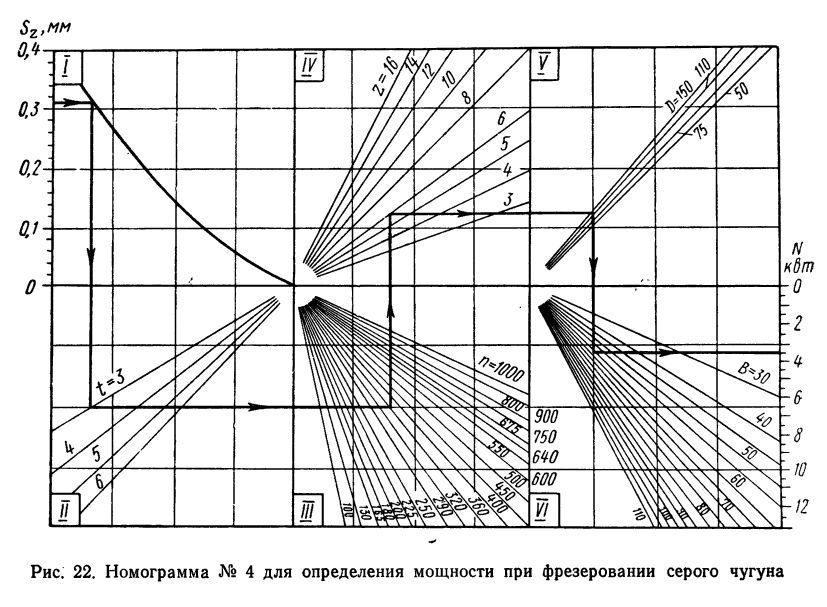
Это был пример достаточно простой номограммы. Ниже я привожу более сложную. Достоинство номограмм в том, что в них умещаются довольно сложные функциональные зависимости с несколькими переменными. В самом деле, сколько бы понадобилось обычных графиков вида $y=f(x)$ для такой задачи?



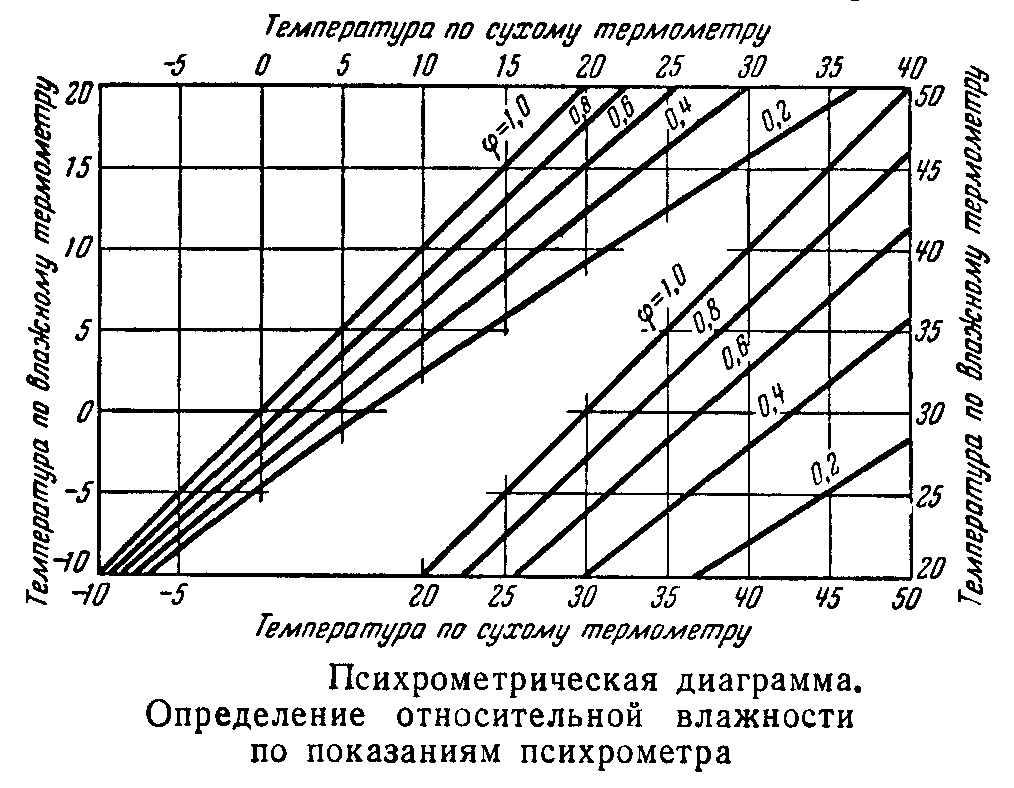
Второй момент — эмпирические формулы бывают сложны для запоминания и неудобны. Вдруг неохота доставать смартфон, искать соответствующую программу, или же вообще тащить с собой компьютер. А так — вот в заводском помещении висит психрометр для замера влажности воздуха, вот номограмма — по ней легко прикинуть влажность.



Разбираемся и делаем свои номограммы


Основания общей теории номографических построений дал Морис Окань (1884—1891) — в его же работах впервые появился термин «номограмма». Книга Traite? de nomographie. The?orie des abaques. Applications pratiques доступна онлайн. Это истоки. Более краткое современное изложение принципов номографии, по которому я учился делать номограммы читайте здесь — The Lost Art of Nomography by Ron Doerfler.


Итак, начнём!


Чтобы сделать номограмму определения температуры кипения при разных давлениях нам понадобится правило Трутона: молярная энтропия испарения разных веществ при нормальной температуре кипения является постоянной величиной. Затем, уравнение Клапейрона — Клаузиуса:


$\frac{d \ln p}{dT} = \frac{\Delta H_{vap}}{RT^2}$


где $\Delta H_{vap}$ — энтальпия испарения, $R$ — газовая постоянная.


Интегрируя последнее уравнение мы получаем:


$\ln \frac{p}{p^*}=-\frac{\Delta H_{vap}}{R}\left( \frac{1}{T}-\frac{1}{T^*}\right)$


где под $p^{*}$ мы обозначим давление 760 мм ртутного столба, а $T^{*}$ — температуру кипения при этом давлении. Нас интересует температура кипения $T$ при пониженном давлении $p$.


Правило Трутона запишем так:


$\Delta S_{vap} = \frac{\Delta H_{vap}}{T} \approx 10.5R$


Подставив последнее выражение, получим расчётную формулу:


$\ln \frac{p}{p^*} = 10.5\left(1-\frac{T}{T^*}\right)$


Её и следует привести в номограмму.


Построение номограмм с pynomo


Следующий шаг — устанавливаем питон-библиотеку pynomo. Тривиально: 


pip install pynomo

Библиотека умеет строить различные номограммы из десяти стандартных блоков.


Нам понадобится стандартный блок номер 2 кодирующий зависимости вида:


$F_1(u_1)=F_2(u_2)\times F_3(u_3)$


где $F_i(u_i)$ — какая-то одномерная функциональная зависимость. Разберём простой пример.


Пусть у нас есть лабораторная центрифуга, для которой мы хотим привести номограмму соответствия числа оборотов ротора в минуту (RPM) с достигаемым центробежным ускорением. Формула следующая:


$a = \omega^2 \times r$


Исходный код номограммы 
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
    rpm.py

    Simple nomogram of type 2: F1=F2*F3
"""
import sys
sys.path.insert(0, "..")
from pynomo.nomographer import *

N_params_RCF={
        'u_min':1000.0,
        'u_max':30000.0,
        'function':lambda u:u,
        'title':r'RCF, $\times g$',
        'tick_levels':3,
        'tick_text_levels':1,
        'tick_side': 'left',
        'scale_type':'linear smart',
        'text_format': r"$%2.0f$",
                }

N_params_r = {'u_min': 1.0,
              'u_max': 5.0,
              'function': lambda u:u,
              'tick_levels': 3,
              'tick_text_levels': 1,
              'tick_side': 'left',
              'text_format': r"$%2.0f$",
              'title':r'R, cm',
              'extra_params': [
                {'u_min':  5.0,
                 'u_max': 10.0,                 
                 'tick_levels': 2,
                 'tick_text_levels': 1,
                 'tick_side': 'right',
                 'text_format': r"$%2.0f$",},
                {'u_min': 10.0,
                 'u_max': 40.0,
                 'scale_type': 'manual line',
                 'manual_axis_data': {10.0: r'10',
                                      12.0: r'12',
                                      14.0: r'14',
                                      16.0: r'16',
                                      20.0: r'20',
                                      24.0: r'24',
                                      30.0: r'30',
                                      40.0: r'40'},
                 },
                ],
            }

N_params_RPM={
        'u_min': 1000.0,
        'u_max':20000.0,
        'function':lambda u:u*u*1.1182e-5,
        'title':r'RPM',
        'tick_levels':3,
        'tick_text_levels':1,
        'scale_type':'linear smart',
        'text_format': r"$%2.0f$",
                }

block_1_params={
             'block_type':'type_2',
             'mirror_y':True,
             'width':10.0,
             'height':10.0,
             'f1_params':N_params_RCF,
             'f2_params':N_params_r,
             'f3_params':N_params_RPM,
             'isopleth_values':[['x',10.0,15200]],
             }

main_params={
              'filename':'RPM.pdf',
              'paper_height':10.0,
              'paper_width':10.0,
              'block_params':[block_1_params],
              'transformations':[('rotate',0.01),('scale paper',)],
              'title_str':r'$a=r\times \omega^2$'
              }
Nomographer(main_params)

Функция $F_3(u_3) = \omega^2$ записывается строкой:


'function':lambda u:u*u*1.1182e-5,

Программа построит номограмму в файл RPM.pdf, ниже на рисунке.



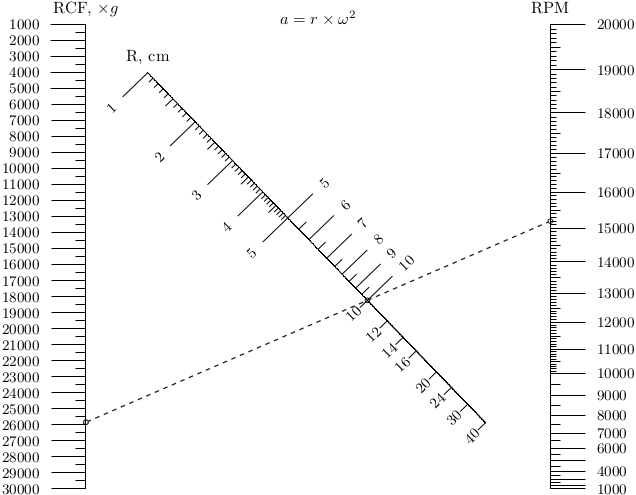
Пунктирная линия называется изоплета — она показывает, как пользоваться номограммой для расчёта достигаемого ускорения (в единицах g) при данной геометрии ротора (радиус вращения) и числа оборотов в минуту (RPM).


Почему этот график так работает? Смотрите чертеж.



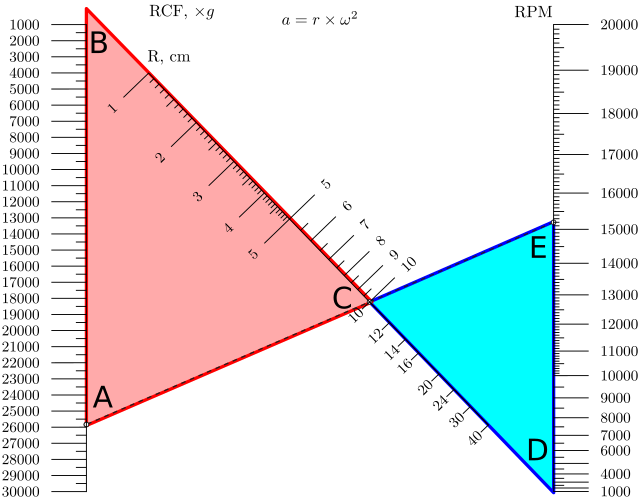
Из него видно, что треугольники ABC и CDE — подобны. Следовательно:


$\frac{AB}{ED} = \frac{BC}{CD} = \frac{BC}{L-BC}$


где L — длина BD, она задана. Пользуясь этим соотношением, можно построить шкалу на L.


Зная этот принцип, мы можем построить номограмму для соотношения


$\ln \frac{p}{p^*}+10.5=\frac{10.5T}{T^*}$


что даст нам номограмму для роторного вакуумного испарителя:



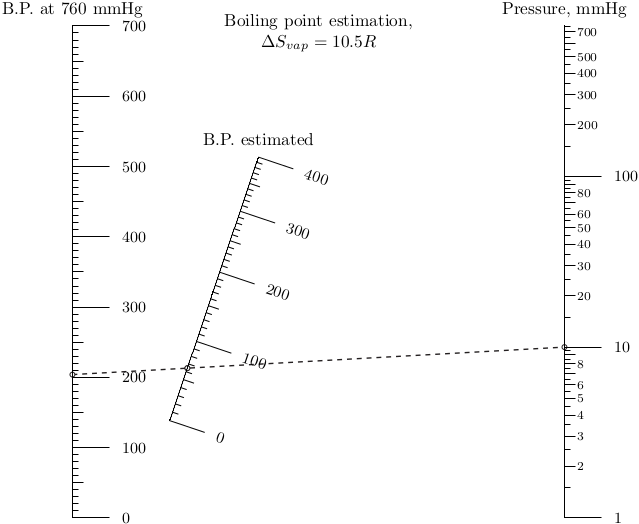
Усложняем номограмму


Теперь, разобравшись с простым примером, перейдем к более сложной зависимости. Воспользуемся уточненным правилом Trouton–Hildebrand–Everett:


$\frac{\Delta H_{vap}}{RT} = (4.5 + \ln T)$


В статье Some calculations for organic chemists: boiling point variation, Boltzmann factors and the Eyring equation. Tetrahedron Letters 41 (2000) 9879–9882 говорится, что для неё не так то просто создать номограмму. Вот и выясним!


Запишем новую зависимость для номограммы:


$\ln \frac{p}{p^*} + T^{*}(4.5 + \ln T^*)\times \frac{1}{T}-(4.5 + \ln T^*) =0 $


Она попадает под случай блока типа 10


$F_1(u)+F_2(v)F_3(w)+F_4(w)=0.$


Теперь ось в середине номограммы может быть не только прямолинейной. Записываем код.


Более сложная номограмма 
from math import log
from pynomo.nomographer import *
import sys
sys.path.insert(0, "..")

Pressure = {
    'u_min':  1.0,
    'u_max': 760.0,
    'function': lambda u: log(u / 760.0),
    'title_y_shift': 0.55,
    'title': r'Pressure, mmHg',
    'tick_levels': 3,
    'tick_text_levels': 2,
    'scale_type': 'log smart',
}

BP_guess = {
    'u_min':  0.0,
    'u_max': 400.0,
    'function': lambda u: 1/(u + 273.15),
    'title_y_shift': 0.55,
    'title': r'B.P. estimated',
    'tick_levels': 4,
    'tick_text_levels': 2,
    'scale_type': 'linear smart',
}

BP_at_atm = {
    'u_min':  0.0,
    'u_max': 700.0,
    'function_3': lambda u: (u + 273.15)*(4.5 + log(u + 273.15)),
    'function_4': lambda u: -(4.5 + log(u + 273.15)),
    'title_y_shift': 0.55,
    'title': r'B.P. at 760 mmHg',
    'tick_levels': 4,
    'tick_text_levels': 2,
    'scale_type': 'linear smart',
}

block_1_params = {
    'block_type': 'type_10',
    'width': 10.0,
    'height': 10.0,
    'f1_params': Pressure,
    'f2_params': BP_guess,
    'f3_params': BP_at_atm,
    'isopleth_values': [[10, 'x', 204]]
}

main_params = {
    'filename': 'ex_type10_nomo_1.pdf',
    'paper_height': 10.0,
    'paper_width': 10.0,
    'block_params': [block_1_params],
    'transformations': [('rotate', 0.01), ('scale paper',)],
    'title_y': 0.55,
    'title_str': r'Boiling point estimation, $\Delta S_{vap} = R(4.5 + \ln T)$'
}

Nomographer(main_params)

Вуаля!



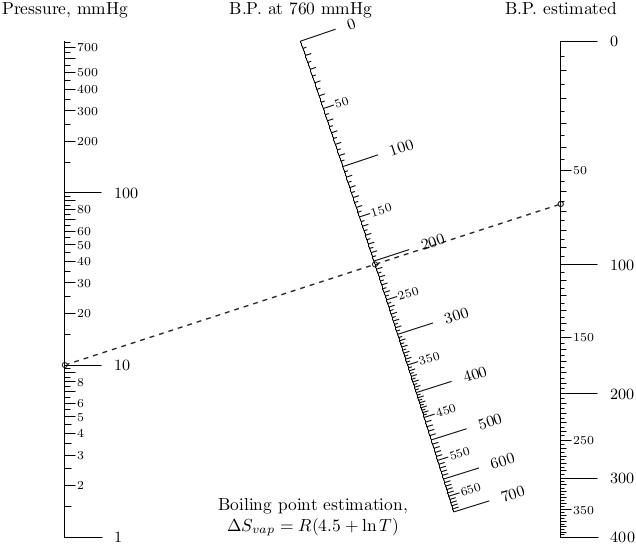
Заключение


Номограммы, как и работающие по схожему принципу логарифмические линейки и другие аналоговые устройства остались в далеком прошлом. Однако, не стоит о них совсем забывать — возможно, вы найдете им новые применения. Или, по крайней мере, найдете их интересным математическим развлечением. Пишите в комментариях о своем опыте.



Облачные серверы от Маклауд быстрые и безопасные.


Зарегистрируйтесь по ссылке выше или кликнув на баннер и получите 10% скидку на первый месяц аренды сервера любой конфигурации!