Первое впечатление
Форт и сейчас известен, главным образом, среди разработки встроенных систем, как что-то вроде необычайного высокоуровневого ассемблера, например, для микроконтроллеров - AmForth и Mecrisp. Однако, когда-то давным давно был известен в другой ипостаси - как язык программирования научных приложений.

Форт был выбран в качестве средства, с помощью которого объясняются детали программной реализации систем, основанных на знаниях, по следующим причинам: во-первых, транслятор с этого языка имеется практически на всех типах микрокомпьютеров, во-вторых, он достаточно дешевый, и, наконец, имеет много общего с языками искусственного интеллекта, в частности с Лиспом.
Таунсенд К., Фохт Д. ПРОЕКТИРОВАНИЕ И ПРОГРАММНАЯ РЕАЛИЗАЦИЯ ЭКСПЕРТНЫХ СИСТЕМ НА ПЕРСОНАЛЬНЫХ ЭВМ. М.: Финансы и статистика, 1990.
Я прочёл это и был впечатлён. Вот три хорошо знакомые мне книги:

Языки программирования в книжках, соответственно - Бейсик, Фортран и Форт! В книге Т. Тоффоли:
CAM-6 является машиной клеточных автоматов, предназначенной для того, чтобы служить лабораторией экспериментатора, средством сообщения результатов и средой для интерактивной демонстрации в режиме реального времени.
Физически CAM-6 состоит из модуля, который вставляется в один разъем IBM-PC (XT, AT или совместимых с ними моделей), и управляющего программного обеспечения, работающего в среде PC-DOS2. В то время как этот легко доступный головной компьютер обеспечивает размещение, экранирование, электропитание, дисковую память, монитор и стандартную операционную среду, вся действительная работа по моделированию клеточных автоматов с очень высокой скоростью совершается самим модулем с быстродействием, сравнимым (для этого частного приложения) с быстродействием CRAY-1. Управляющее программное обеспечение для CAM-6 написано на FORTH и работает на IBM-PC с памятью 256 К. Это программное обеспечение дополнено рядом готовых приложений и демонстрационных примеров и включает полный аннотированный список источников.
В этой книге будет использоваться язык CAM Forth. Forth является расширяемым языком программирования, особенно подходящим для интерактивных задач. Этот язык был расширен так, чтобы он содержал множество слов и конструкций, полезных для поддержания диалога с CAM ( в частности, для определения правил клеточного автомата и для конструирования, документирования и выполнения экспериментов).
Очень интересно! Убедили, я тоже хочу попробовать Форт! Ощутить, как это, писать научное приложение на уровне 80-х или ранних 90-х. Говорят, что каждый фортер пишет свой Форт, но вряд ли это кому-то еще интересно, так что, пожалуй, попробую воспользоваться каким-то готовым Фортом и написать, скажем, программу для численного испытания... А, пускай будет это: C. Clay Marston and Gabriel G. BalintKurti. The Fourier grid Hamiltonian method for bound state eigenvalues and eigenfunctions // J. Chem. Phys. 91, 3571 (1989); doi: 10.1063/1.456888
Как будто на дворе 1989 год, компилятор Фортрана где-то на большой машине в институте, а у меня просто нечто под руками, никаких там Matlab в помине нет. Компьютер - чуть больше по своим возможностям, чем калькулятор.
Знакомство
Кстати, а вот и он - HP 35s. Программы в нём - шитый код (ниже рисунок из Руководства к калькулятору). Перейти с калькулятора на Форт очень просто - Форт тоже использует тот самый шитый код.

В самом деле, каждое слово (термин Форта, аналог процедур или функций) состоит из других слов и так до самого нижнего уровня, где слова-примитивы это просто машинный код.
see normcdf
: NORMCDF flit 1.41421 F/ ERF F1.0 F+ flit .500000 F* ;
ok
see erf
: ERF FDUP FSIGN FSWAP FDUP F* FDUP flit .147000 F*
FDUP flit 1.27324 F+ FSWAP F1.0 F+ F/ F*
FNEGATE FEXP FNEGATE F1.0 F+ FSQRT F* ;
ok
see fsign
: FSIGN F0< DUP INVERT - S>F ;
ok
see dup
DUP IS CODE ( $4012D8 53 )
push ebxВ Форте всё слова. Константа - слово, что оставляет на стеке число. Переменная оставляет на стеке адрес, где лежит её значение. Есть много разных книг и описаний Форта, не буду их повторять, однако, считаю, что одно из лучших описаний того, что и как происходит под капотом дано здесь - http://rigidus.ru/
По моему впечатлению, Форт язык прагматичный, а не парадигматичный. Это постфиксный язык? С одной стороны, да, с другой - не совсем. Вот скажем, если последовательно придерживаться постфиксной записи, то определения должны были бы быть наподобие следующего:(word) cvn { moveto show } def или { moveto show } /S exch def где ключевое слово def (определить) стоит после самого определения. Так делается в Postscript, но не в Форт. В Форте было бы : word moveto show ; - за двоеточием следует определяемый термин, точка с запятой завершает определение. Почему так? А так проще. Двоеточие переводит интерпретатор Форт в состояние компиляции STATE=-1 (true в Форте), и текст определения считывается слева на право, точка с запятой в состояние интерпретации (выполнения) STATE=0.
Многие вещи в Форте сделаны с упором на простоту реализации, а не стандартизации. Чак Мур, создатель Форта, плохо относится к стандартизации. Его принцип - тебе нужно, ты и сделай. Не спекулируй, не оставляй зарубки для удобства будущего расширения функционала. Сейчас удобно и просто делать ТАК, вот ТАК и делай САМ И ПРЯМО СЕЙЧАС. Короче говоря, Форт это не совсем язык, это метод решения конкретных проблем. Вот его кредо:
Keep it simple
Do not speculate
Do it yourself
motherf*cker
Не ждите от Форта серебряной пули, крутого фреймворка, полной библиотеки и продуманного кем-то API. Вот вам мнения, целый зоопарк реализаций и рецептов - да поможет Вам здравый смысл и базовые три принципа.
Стеквилибристика
Положим, что мы захотели реализовать вычисление гамма-функции (точнее, её логарифма) на Форте. Более того, у нас имеется сопроцессор типа Intel 8087 - у него стековая архитектура, очень кстати для Форта! Воспользуемся приближением Ланцоша и запишем:
: LNGAMMA ( x -- ln(Г(x) )
\ Takes x > 0.0 and returns natural logarithm of Г(x).
FDUP 3.0E F+ 2.23931796330267E FSWAP F/
FOVER 2.0E F+ -27.0638924937115E FSWAP F/ F+
FOVER 1.0E F+ 41.4174045302371E FSWAP F/ F+
2.5066284643656E F+ FLN FSWAP
FDUP 4.15E F+ FLN
FOVER 0.50E F+ F*
FOVER 4.15E F+ F-
FROT F+ FSWAP FLN F- ;Да, выглядит не очень читаемо - не все формулы хорошо укладываются в операции со стеком и чем сложнее - тем больше будет слов FDUP, FROT, FOVER... пока не настанет ситуация, когда на стеке 4 и более чисел. Тогда всё, приплыли. Печальная история о том, как такое случается изложена в одном блоге.
Обычный выход из этого положения - локальные переменные. Да, это Форт, их можно реализовать разными способами. Например, так : lngamma { f: x } это способ gforth. Или так : lngamma {: f: x :} способ VFX Forth. Локальные переменные достаточно сложная концепция, включающая в себя область видимости, время жизни и прочее. Вот уже придется нарушить первый принцип Форт и превратить его в Си-подобный язык?
Гиперстатическое глобальное окружение
Строго говоря, глобальные переменные Форта это совсем не тоже самое, что в других языках. Чтобы было понятнее, вот пример рабочего кода:
variable apples ok
: +apples apples +! ; ok
: apples ." You have " apples @ . ." apples." cr ; ok
apples You have 0 apples.
ok
5 +apples ok
apples You have 5 apples.
okЗдесь переменная apples переопределена словом apples, которое сообщает текущее количество яблок. Однако, слово +apples работает как положено, увеличивая счётчик. Внутри слова +apples ссылка на адрес счётчика, а не имя переменной. Так мы можем изменить любое определение не затрагивая работу ранних определений. Например, нам нужна переменная X. Определим:
variable &x
: x &x @ ;
: (x) &x ! ;
: cube (x)
x x x * * ;
variable &x
: x &x @ ;
: (x) &x ! ;
: square (x)
x x * ;
3 square . 9 ok
3 cube . 27 okСлова cube и square работают как положено. Повторяющиеся слова &x, x, (x) можно спрятать за определяющим словом, наподобие того, как предложено тут, см. пост FORTH: Самоопределяющиеся слова.
Определение группы переменных в F-PC Forth 3.60
FLOAD FFLOAT.SEQ
FLOAD EVAL.SEQ
: COMPARE ( c-addr1 u1 c-addr2 u2 -- n )
ROT
2DUP U< IF DROP COMPARE DUP 0= IF DROP 1 THEN EXIT THEN
2DUP U> IF NIP COMPARE DUP 0= IF DROP -1 THEN EXIT THEN
DROP COMPARE ;
: REFILL ( -- f ) \ CORE version for user input device and string only
loading @ IF ( file ) false EXIT THEN
'tib @ sp0 @ = IF ( user input device ) query true EXIT THEN
( EVALUATE ) false ;
MACRO: ++ PAD +PLACE ;
: (VARIABLE)
" VARIABLE &" PAD PLACE 2DUP ++
" : (" ++ 2DUP ++ " ) &" ++ 2DUP ++ " ! ;" ++
" : " ++ 2DUP ++ " &" ++ ( NAME ) ++ " @ ;" ++
PAD COUNT EVAL ;
: (FVARIABLE)
" FVARIABLE &" PAD PLACE 2DUP ++
" : (" ++ 2DUP ++ " ) &" ++ 2DUP ++ " F! ;" ++
" : " ++ 2DUP ++ " &" ++ ( NAME ) ++ " F@ ;" ++
PAD COUNT EVAL ;
: REFILL-AT-EOL? ( S: -- FLAG )
SOURCE NIP >IN @ > DUP 0= IF DROP REFILL THEN ;
: VARIABLES(
BEGIN BL WORD COUNT 2DUP " )" COMPARE
WHILE REFILL-AT-EOL?
WHILE (VARIABLE)
REPEAT
THEN 2DROP ;
: FVARIABLES(
BEGIN BL WORD COUNT 2DUP " )" COMPARE
WHILE REFILL-AT-EOL?
WHILE (FVARIABLE)
REPEAT
THEN 2DROP ;Так оно будет использоваться так:
\ Объявление переменных
VARIABLES( MAXIT )
FVARIABLES( ACCURACY UNLIKELY-VALUE )
\ Присвоение значений
-1.11E30 (UNLIKELY-VALUE)
1.0E-9 (ACCURACY)
50 (MAXIT)
\ Положить значение переменной на стек
MAXIT . 50 okПольза от выбранной нотации, по сравнению с обычными переменными Форта, заключается в том, что гораздо чаще с переменной значение считывается, а не записывается. Таким образом, вместо x @ y @ + z ! будет x y + (z), и многочисленные @ и f@ будут факторизованы.
F-PC Forth
Для аутентичного погружения в старые добрые времена IBM PC AT, MS DOS и всё такое, я выбрал F-PC Forth. Скачать fpc36.zip, распаковать, запускать под dosbox. Работает всё из коробки, легко и просто.

Это полноценная IDE, с редактором кода, отладчиком и интерактивной справкой. Удобные IDE не только Borland делал.
больше ретро экранов F-PC Forth 3.60
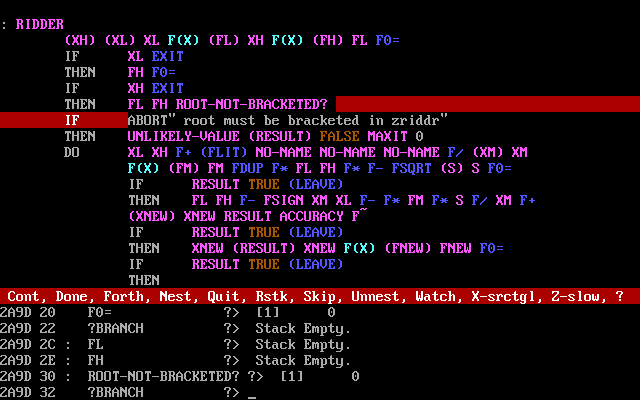

Написал в этом старом Форте код для поиска корней уравнения методом Риддера. Для сравнения здесь есть код на Julia.
Поиск корня уравнения методом Риддера на F-PC Forth 3.60
DEFER F(X)
VARIABLES( MAXIT )
FVARIABLES( XL XM XH XNEW FL FM FH FNEW S RESULT ACCURACY UNLIKELY-VALUE )
-1.11E30 (UNLIKELY-VALUE)
1.0E-9 (ACCURACY)
50 (MAXIT)
: FSIGN ( R1 -- R1 ) F0< DUP NOT - IFLOAT ;
: F~ ( R1 R2 R3 -- FLAG ) F-ROT F- FABS F> ;
: ROOT-NOT-BRACKETED? ( FL FH -- FLAG )
FDUP F0< FOVER F0> AND
( FB ) F0> ( FA ) F0< AND OR NOT ;
: RIDDER ( R1 R2 -- R1 ) (XH) (XL)
XL F(X) (FL) XH F(X) (FH)
FL F0= IF XL EXIT THEN
FH F0= IF XH EXIT THEN
FL FH ROOT-NOT-BRACKETED?
IF ABORT" ROOT MUST BE BRACKETED IN ZRIDDR" THEN
UNLIKELY-VALUE (RESULT) FALSE
MAXIT 0
DO
XL XH F+ 2.0E F/ (XM) XM F(X) (FM)
FM FDUP F* FL FH F* F- FSQRT (S)
S F0=
IF RESULT TRUE LEAVE THEN
FL FH F- FSIGN XM XL F- F* FM F* S F/ XM F+ (XNEW)
XNEW RESULT ACCURACY F~
IF RESULT TRUE LEAVE THEN
XNEW (RESULT) XNEW F(X) (FNEW)
FNEW F0=
IF RESULT TRUE LEAVE THEN
FNEW FSIGN FM F* FM F= NOT
IF XM (XL) FM (FL) RESULT (XH) FNEW (FH)
ELSE FNEW FSIGN FL F* FL F= NOT
IF RESULT (XH) FNEW (FH) THEN
FNEW FSIGN FH F* FH F= NOT
IF RESULT (XL) FNEW (FL) THEN
THEN
XL XH ACCURACY F~
IF RESULT TRUE LEAVE THEN
LOOP
IF RESULT DROP
ELSE ." ZRIDDR EXCEED MAXIMUM ITERATIONS" DROP THEN ;
: FUNC FDUP FEXP FSWAP -5.0E F* 3.0E F+ F+ ;
' FUNC IS F(X)
1.25E 1.6E RIDDER F.Кажется, получилось вполне читаемо, особенно если сравнивать с языками тех времен: BASIC, Fortran 77, Pascal.
Структуры, массивы, матрицы
Форт не идет в комплекте с батарейками, но позволяет самому легко задать необходимые конструкции. Не стоит увлекаться чрезмерно общими вещами, ограничимся тем минимумом, что работает. Начнем со структур.
\ Structures
: structure:
create ( structure name ) here 0 0 ,
does> @ ;
: +field
create ( field name ) over , +
does> @ + ;
: (cell) aligned 1 cells +field ;
: (float) faligned 1 floats +field ;
: end-structure ( addr size -- ) swap ! ;Здесь я уже переключился на более современный Форт, стандарта 1994. В сущности, F-PC может быть дополнен до этого стандарта, и код ANS Forth 94 поддерживается современными компиляторами, например, win32forth, Gforth. Следуя духу ретро, я писал код в win32forth.
У него тоже есть IDE и другие удобства, работает под Windows (под wine запускается без проблем). Структуры полезны при определении векторов и матриц, например:
\ Arrays
structure: array-structure
(cell) .array-data
(cell) .array-type
(cell) .array-size
end-structure
: array: ( size -- )
create
0 here .array-data ! here .array-type ! here .array-size !
array-structure allot ;
: array-allocate ( vec -- )
>r r@ .array-size @ r@ .array-type @ * allocate throw r> .array-data ! ;
: array-free ( vec -- )
>r r@ .array-data @ free throw 0 r> .array-data ! ;
: array-element ( i vec -- *vec[i] )
>r r@ .array-type @ * r> .array-data @ + ;Критические по времени функции нужно выполнить в ассемблере, это даст прирост скорости матричных вычислений 3-5 раз. Работы не много. Ниже код для доступа к элементу массива чисел с плавающей запятой.
code fs-array-element
pop eax
mov ebx, [ebx]
lea ebx, [ebx] [eax*8]
next c;Существует библиотека математических функций Форта - The Forth Scientific Library Project, впрочем, там всё равно нет реализации алгоритма вычисления собственных значений симметричной действительной матрицы. Do it yourself! Берем книгу Голуб, Ч. Ван Лоун. Матричные вычисления и реализуем алгоритм Якоби.
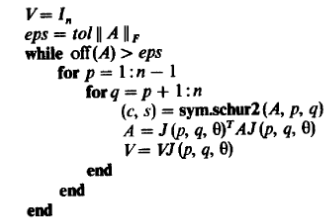
\ Cyclic Jacobi. Algorithm 8.5.3
\ Golub & Van Loan, Matrix Computations
fvariables( cos sin EPS )
variables( M EV MAXROT )
1.0e-10 (EPS)
50 (MAXROT)
: eig! (EV) (M)
EV matrix-set-identity!
MAXROT 0
do
M off-diagonal-norm EPS f<
if unloop exit then
M .matrix-rows @ 0
do M .matrix-cols @ i 1+
?do i j M sym.schur2 (sin) (cos)
cos sin i j M jacobi.rot'
cos sin i j M jacobi.rot
cos sin i j EV jacobi.rot
loop
loop
loop
." jacobi not converged" ;Симпатично, практически псевдокод? В этом и есть смысл Форта - создавать лексикон той области, в которой решается проблема. Вспомогательные слова к главному определению eig я опускаю, каждое содержит не больше строк, чем eig.
Финал
Настало время решать поставленную задачу, а именно, согласно статье C. Clay Marston and Gabriel G. BalintKurti. The Fourier grid Hamiltonian method for bound state eigenvalues and eigenfunctions // J. Chem. Phys. 91, 3571 (1989); doi: 10.1063/1.456888 реализовать метод и посчитать, допустим, уровни энергии осциллятора Морзе. Иными словами, превратить рассуждения из фрагмента статьи ниже в практику.

Последовательность действий:
Вычисляем суммы из уравнения (26)
Формируем тёплицеву матрицу H
Создаем дискретную сетку по оси X
Табулируем потенциал V(x) в точках сетки
Добавляем табулированный потенциал к диагонали матрицы H
Находим собственные числа и собственные векторы (это и есть решение)
Суть метода Fourier grid Hamiltonian (FGH) умещается в два определения Форта:
\ Equation 26
fvariables( l d/N )
: sum (d/N)
1.0e (l)
0.0e ( N ) 1 rshift 0
do [ 2.0e fpi f* ] fliteral
l d/N f* f* fcos l f**2 f* f+
l 1.0e f+ (l)
loop ;
variables( diags n )
fvariables( dx 1/n )
: FGH! (diags) (dx)
diags .array-size @ (n)
n s>f 1/f (1/n)
[ -8.0e fpi f**2 f* ] fliteral
1/n fdup fdup f* f* f* dx f**2 1/f f*
n 0 do i s>f 1/n f* n sum fover f* i diags fa!
loop fdrop ;Дальше идёт обычный boilerplate code как объявления матриц, векторов, инициализация элементов, затем поиск собственных значений и распечатка результатов. На этом этапе стоит как следует поиграть с параметрами и воспользоваться интерактивностью Форта. Мы же как будто в прошлом, так? Никакого python/numpy, Matlab и Julia - просто усовершенствованный калькулятор.

Кому интересно, смотрите, я выложил код на гитхабе.
Заключение
Форт вполне себе мог c успехом заменять Fortran и что там еще было в то время. Не так то сложно жить с постфиксной записью, стеками и иметь дело с уровнем чуть выше машинных команд. Немаловажно и то, что результатом процесса работы над какой-то задачей в Форте будет или "нет, ну его ко всем чертям, где там это уже сделали, проще списать", или очень глубокое понимание каждой детали и сути происходящего.
Это всё философия, конечно. Однако, я могу себе представить какой-то численный Форт и сейчас, в наше время. Он может оказаться где то глубоко в оборудовании хитрого спектрометра, детектора... Было бы интересно узнать, где.



Alyoshka1976
В добрые старые времена каждое (наверно) повествование о Форте не обходилось без упоминания того, что его первым практическим применением было управление радиотелескопом. Жив ли сейчас тот аппарат и что им управляет…