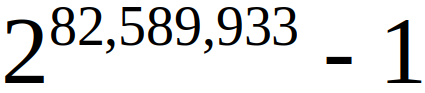
(Примечание переводчика: не нашёл публикации (-ий) по данной теме на Хабре.)

Блоуинг Рок, Северная Каролина, 21 декабря 2018 года — организация Great Internet Mersenne Prime Search (GIMPS, масштабный Интернет-проект по поиску простых чисел Мерсенна) обнаружила самое большое известное простое число 2^82589933 - 1, состоящее из 24 863 048 знаков. Компьютер добровольца Патрика Ляроша вычислил его 7 декабря 2018 года. Патрик — один из тысяч, использующих бесплатное ПО GIMPS.

Новое простое число, также известное как M82589933, вычислено перемножением 82 589 933 двоек и вычитанием единицы. Оно превосходит предыдущее рекордное простое число более чем на полтора миллиона разрядов, в особом классе исключительно редких простых, известных как числа Мерсенна. Это всего пятьдесят первое открытое простое число Мерсенна; вычисление каждого последующего становится сложнее. Простые числа Мерсенна названы по имени французского монаха Марина Мерсенна, изучавшего эти числа больше 350 лет назад. Основанная в 1996 году GIMPS обнаружила последние 17 простых чисел Мерсенна. Для поиска этих простых чисел скачивают бесплатную программу, и есть шанс выиграть денежный приз, если повезёт найти новое число. У профессора Криса Колдуэлла есть авторитетный веб-сайт, посвящённый самым большим известным простым числам с замечательной историей простых чисел Мерсенна.

Патрик Лярош — 35-летний IT-шник, живущий в Окале, штат Флорида. Патрик использовал ПО GIMPS для стресс-тестов. Недавно он начал искать простые числа, чтобы "отдать долг" проекту. За своё открытие он получил от GIMPS исследовательскую награду в 3 000 долларов.

Клиентское ПО Prime95 разработано основателем GIMPS Джорджем Уолтманом. Скотт Куровски написал системное ПО PrimeNet, координирующее компьютеры GIMPS. Аарон Блоссер теперь работает системным администратором и при необходимости выполняет обновление и обслуживание PrimeNet. Волонтёры имеют шанс получить вознаграждение в 3 000 или 50 000 долларов, если их компьютер откроет новое простое число Мерсенна. Следующей крупной целью GIMPS является выигрыш учреждённой Electronic Frontier Foundation награды в 150 000 долларов, которая будет вручена за нахождение простого числа со 100 000 000 десятичных разрядов.

Мы признательны за нахождение этого простого числа не только Патрику Лярошу, выполнявшему на своём компьютере ПО Prime95: Уолтману за написанное ПО, Куровски и Блоссеру за их работу с сервером Primenet, а также тысячам добровольцев GIMPS, просеявшим миллионы вариантов чисел. В благодарность всем этим людям официально это открытие приписывается «Дж. Пейсу, Дж. Уолтману, С. Куровски, А. Блоссеру и коллегам».

Про Great Internet Mersenne Prime Search

Организация Great Internet Mersenne Prime Search (GIMPS) была сформирована в январе 1996 года Джорджем Уолтмана для нахождения новых мировых рекордов простых чисел Мерсенна. В 1997 году Скотт Куровски обеспечил GIMPS возможность использовать мощь тысяч обычных компьютеров для поиска этих «иголок в стоге сена». Большинство участников GIMPS вступило в организацию ради захватывающей возможности обнаружения рекордного, редкого и исторического нового простого числа Мерсенна. Поиск следующих простых чисел Мерсенна уже продолжается. Возможно, существуют и меньше, но пока ненайденные простые, и почти абсолютно точно есть бОльшие, ждущие своего обнаружения. Любой человек с достаточно мощным компьютером может присоединиться к GIMPS и стать охотником за большими простыми числами с возможностью получить денежную награду за своё открытие. Всё необходимое ПО можно бесплатно скачать по адресу www.mersenne.org/download/. GIMPS сформирована как Mersenne Research, Inc., некоммерческая научная благотворительная организация 501(с)(3). Подробнее об этом можно прочитать на www.mersenneforum.org и www.mersenne.org; также принимаются добровольные пожертвования.

Дополнительная информация о простых числах Мерсенна

Простые числа давно восхищали и любителей, и профессионалов математики. Целое число больше единицы называется простым числом, если его единственными делителями являются единица и оно само. Первые простые числа: 2, 3, 5, 7, 11 и т.д. Например, число 10 не является простым, потому что делится на 2 и 5. Простое число Мерсенна — это простое число, имеющее вид 2^P - 1. Первыми простыми числами Мерсенна являются 3, 7, 31 и 127, соответствующие P = 2, 3, 5 и 7. Пока известно 50 простых чисел Мерсенна. Простые числа Мерсенна были в центре внимания теории чисел с тех пор, когда их впервые рассмотрел Евклид около 350 до нашей эры. Человек, именем которого назвали эти числа, французский монах Марин Мерсенн (1588-1648 гг.), создал знаменитую гипотезу о том, при каких значениях P можно получить простое число. Чтобы подтвердить эту гипотезу, потребовались 300 лет и несколько важных открытий.

Сегодня есть мало практических применений этого простого числа, что заставляет некоторых задаваться вопросом: «Зачем вообще искать такие большие простые числа»? Подобные сомнения существовали и несколько десятилетий назад, пока, наконец, не были разработаны важные криптографические алгоритмы на основе простых чисел. Ещё семь хороших причин для поиска больших простых чисел изложены здесь.

Предыдущие открытия простых чисел Мерсенна в рамках GIMPS были совершены участниками из разных стран.

Евклид доказал, что каждое простое число Мерсенна генерирует совершенное число. Совершенное число — это число, сумма собственных делителей которого равно самому числу. Самым малым совершенным числом является 6 = 1 + 2 + 3, вторым — 28 = 1 + 2 + 4 + 7 + 14. Эйлер (1707-1783 гг.) доказал, что все чётные совершенные числа являются результатом произведения простого числа Мерсена на два в степени p-1: 2^(p-1)*(2^p-1). Последнее открытое совершенное число — это 2^77232916 x (2^77232917-1). Это число имеет более 49 миллионов разрядов! Всё ещё неизвестно, существуют ли нечётные совершенные числа.

Арифметические алгоритмы, лежащие в основе проекта GIMPS, имеют уникальную историю. Программы, нашедшие последние большие простые числа Мерсенна, основаны на специальном алгоритме. В начале 1990-х ныне покойный Ричард Крэндэлл, выдающийся учёный из Apple, обнаружил способы удвоения скорости выполнения свёрток — очень больших операций умножения. Этот метод применим не только ко поиску простых чисел, но и к другим аспектам вычислений. В процессе работы над этим проектом он также запатентовал систему шифрования Fast Elliptic Encryption, которая теперь принадлежит Apple Computer. В ней для быстрой шифровки и дешифровки сообщений используются простые числа Мерсенна. Джордж Уолтман реализовал алгоритм Крэндэлла на языке ассемблера, создав таким образом программу поиска простых чисел с беспрецедентной эффективностью. Эта работа привела к созданию успешного проекта GIMPS.

Школьные учителя используют GIMPS, чтобы заинтересовать своих учеников математикой. Студенты, запустившие на своих компьютерах ПО, вносят свой вклад в математические исследования.